
3次関数のグラフの最大値・最小値(数学Ⅱ)
対象学年:高校二年生
教科:数学Ⅱ
単元:微分法と積分法
作成者:高校教師
更新日:2021年12月28日
※ライセンスをお持ちでないEX-wordふせんは表示されません
■授業概要
「微分法と積分法」にてClassPad.netの数学ツール「ClassPad Math」を使ってグラフを動かして見せることで、定義域が変化する場合の最大値・最小値や場合分けの重要性を視覚的に理解できます。また、生徒自身がグラフを動かして最大値・最小値を求めた後、演習問題に取り組むことで知識の定着を狙います。
■ClassPad.net活用のポイント
・数学ツール「ClassPad Math」の利用で
1. グラフ機能を使ってパラメーターを変化させて最大値・最小値の変化を視覚的に見せることで、理解を深めることができる
2. 生徒自身がグラフを動かして、最大値・最小値の変化を実感することで、知識を効果的に定着させることができる
・授業支援機能の利用で
1. プリントの配布・印刷の手間を省き、その分他の活動に集中することができる
2. 生徒の進捗状況を一覧で確認することができる
■活用法動画(展開部分)
■指導案(詳細はダウンロードしてご覧ください)

■ClassPad.net活用のポイント
STEP1: 変数を含んだ定義域における最小値解法を解説しましょう
STEP2: 同問題の最大値を求めてみましょう
STEP3: 最大値の解法を解説しましょう
STEP4: 類題を解いてみましょう
STEP1: 変数を含んだ定義域における最小値解法を解説しましょう
1-1:まずは例題を配布しましょう

【POINT】pdfデータをデジタルノートに貼付けておくと、配布もスムーズです
1-2:数学ツール「ClassPad Math」を用いて、視覚的に最小値を求める方法を解説しましょう
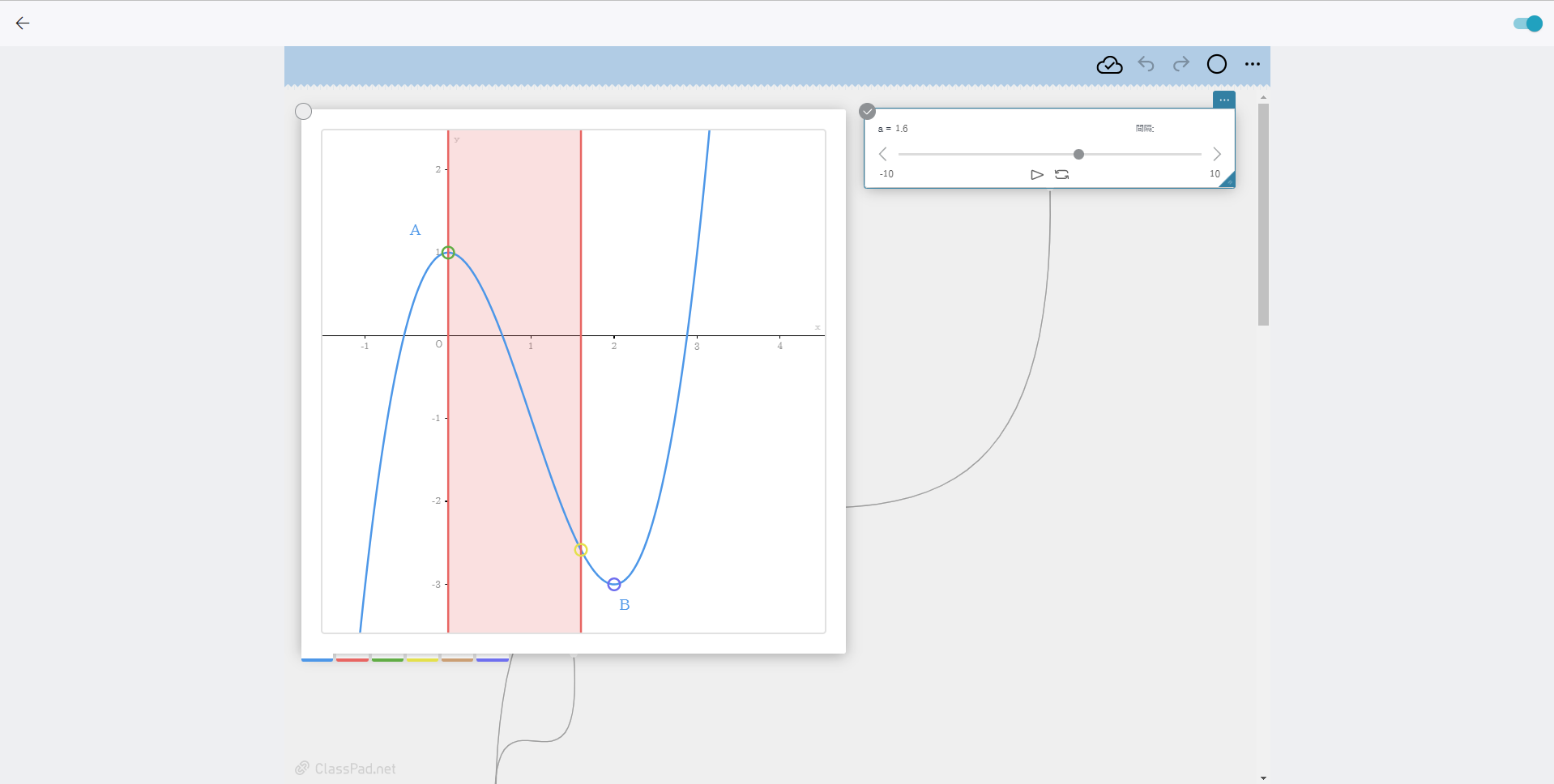
[a=1.6の場合]
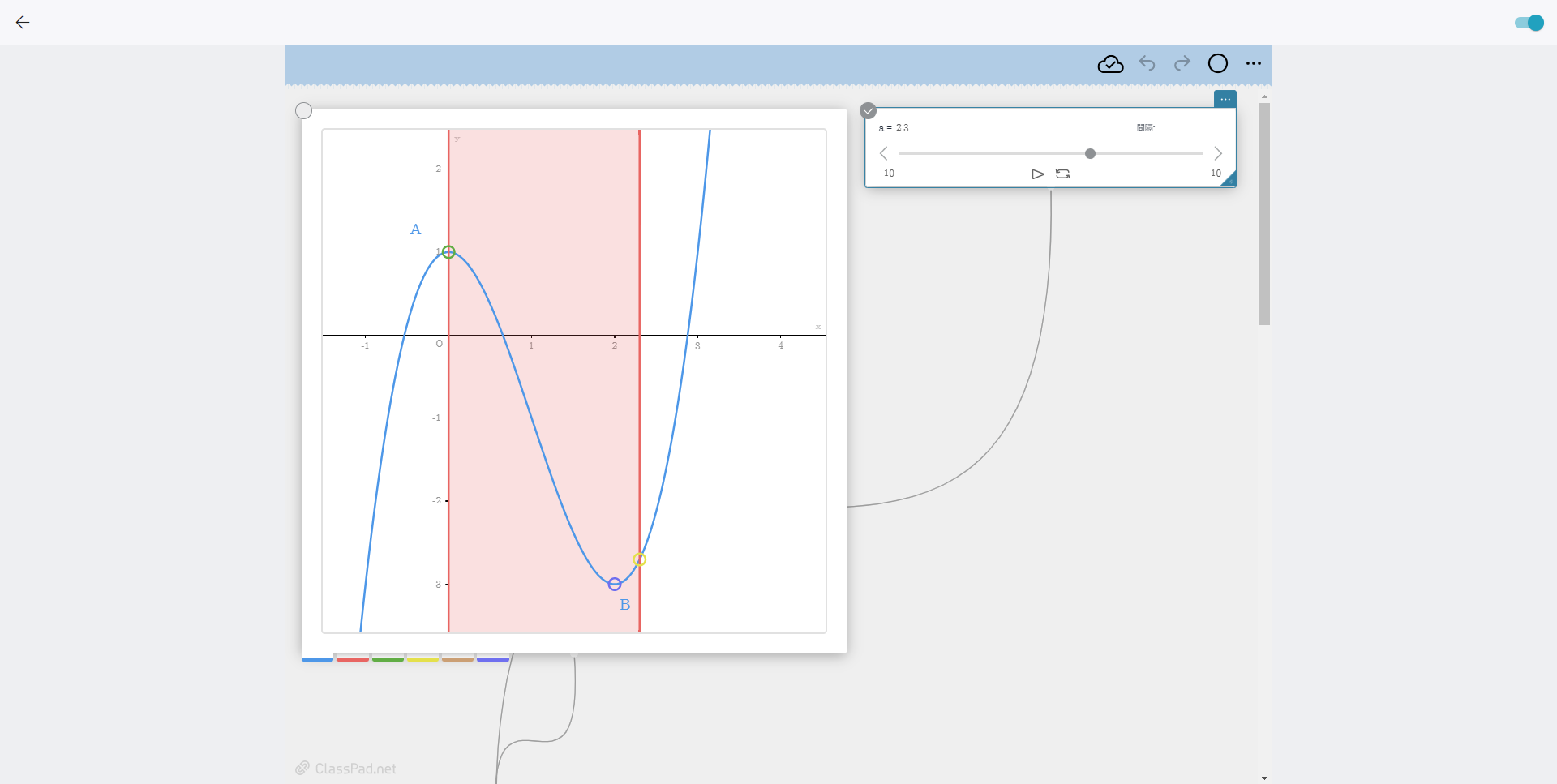
[a=2.3の場合]
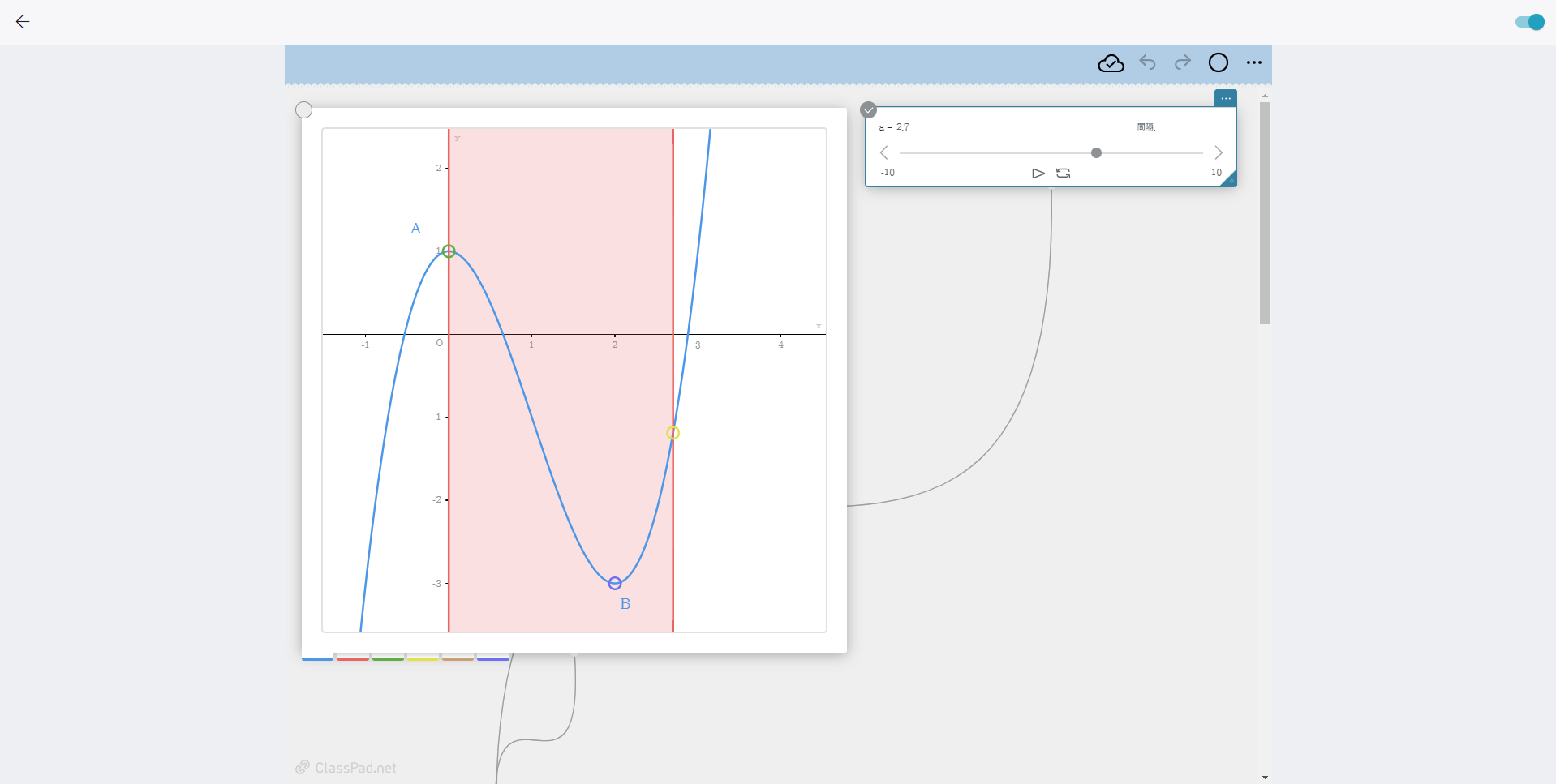
[a=2.7の場合]
【POINT】数学ツール「ClassPad Math」を活用して定義域を徐々に変化させる様子を動的に見せることで、理解を促進します
STEP2: 同問題の最大値を求めてみましょう
2-1: <先生>まずはグラフデータを生徒に配布しましょう
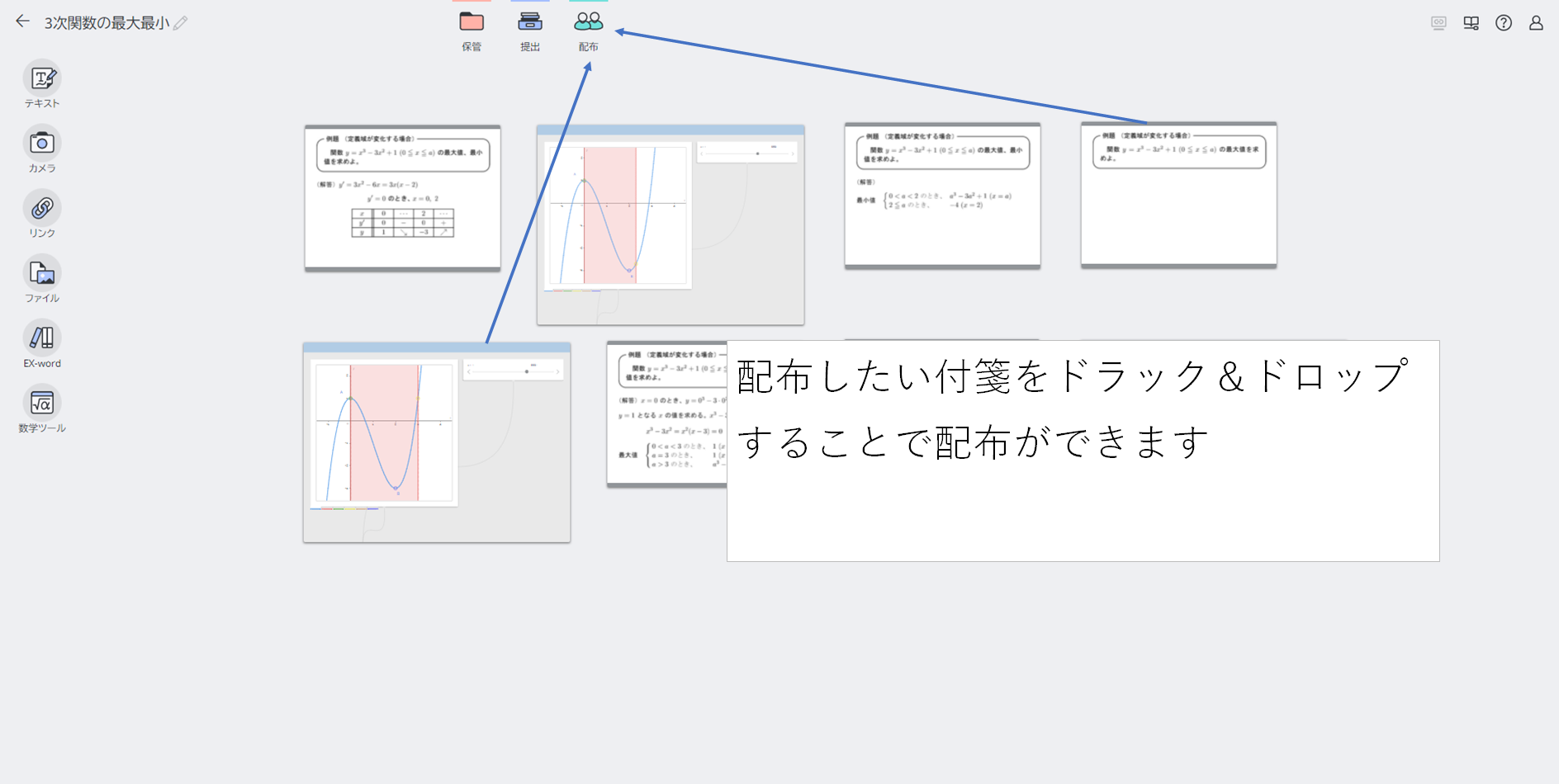
【POINT】グラフデータを生徒に配布することで、問題を解く時間をより多く確保できます
2-2: <生徒>グラフデータを受け取り、最大値を求めましょう
◇STEP3: 最大値の解法を解説しましょう
3-1: 数学ツール「ClassPad Math」を用いて最大値の解説を行いましょう
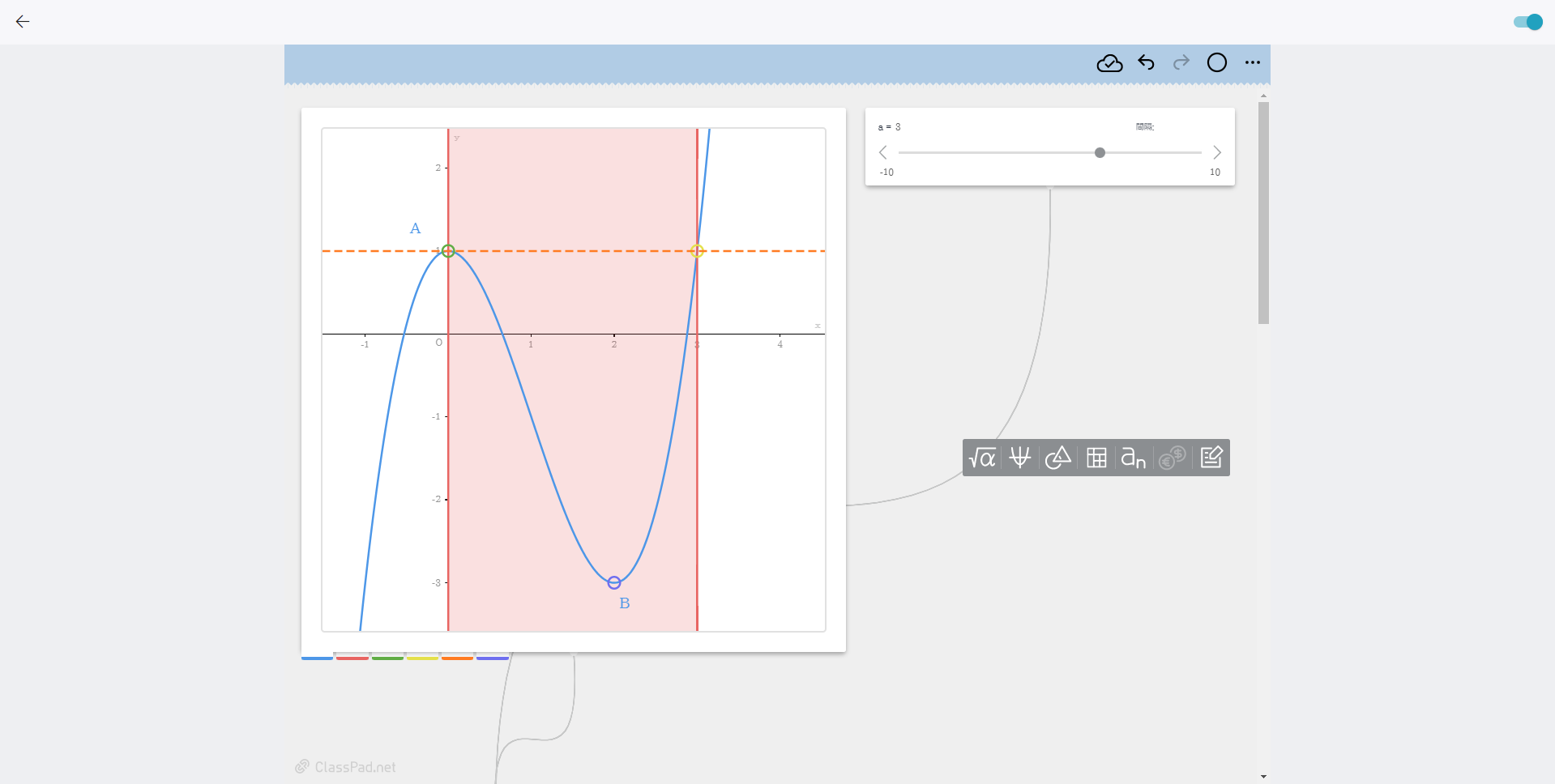
【POINT】a=3の時に、最大値を取るxの値が2つになることに注意をし、解説を行います
◇STEP4: 類題を解いてみましょう
4-1: <先生>生徒に類題およびグラフデータを配布します
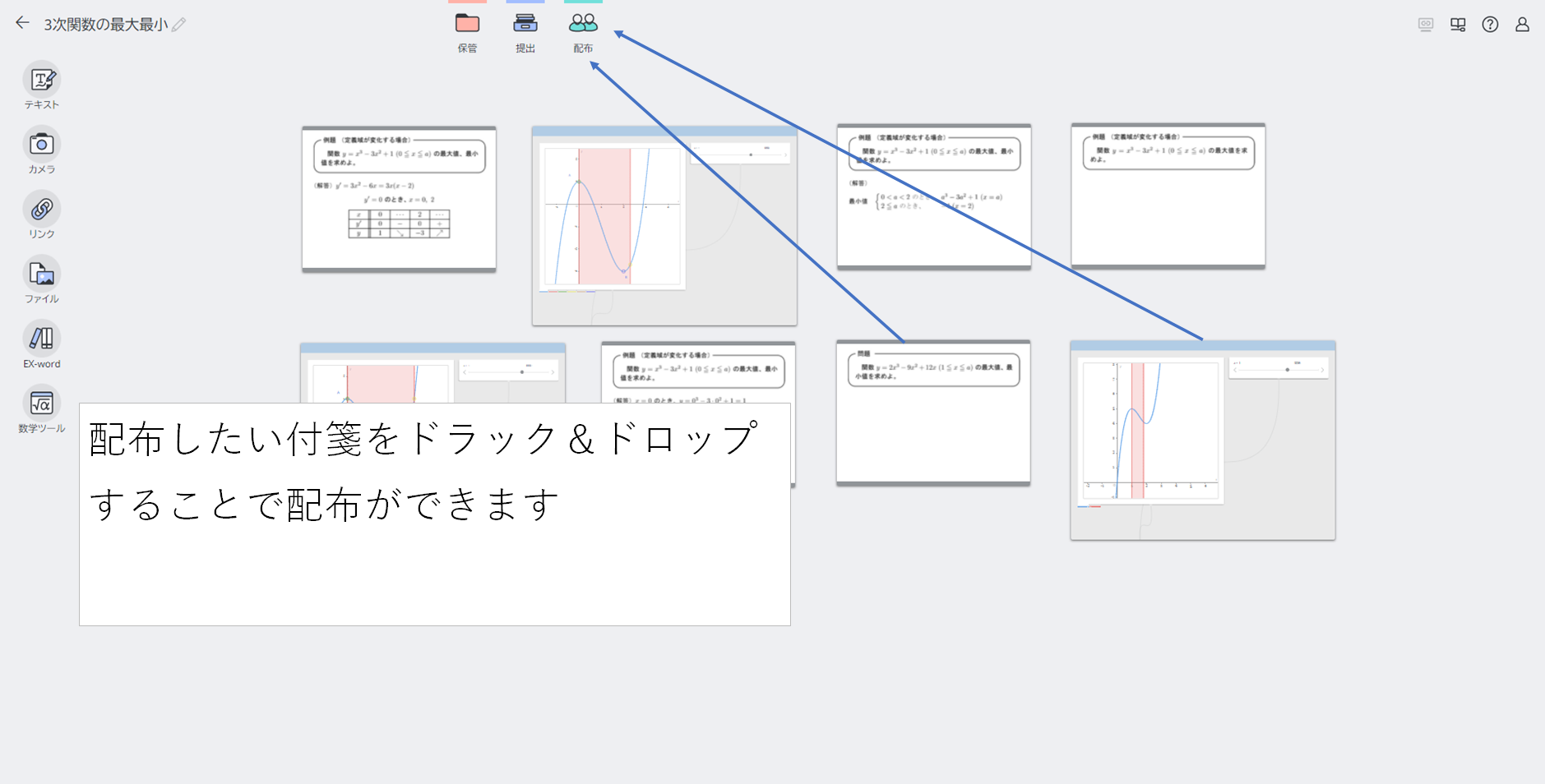
【POINT】類題のグラフデータを事前に準備をしておくことで、スムーズに類題の配布を行い事ができます
4-2: <生徒>配布されたデータを受け取り、類題に取り組みましょう


