Edistynyt

solve

Palauttaa yhtälön tai epäyhtälön juuren.
Syntaksi 1: solve(Exp/Eq/Ineq [, Muuttuja] [ ) ]

• “\(x\)” on oletus, kun ohitat ”[, Muuttuja]”.

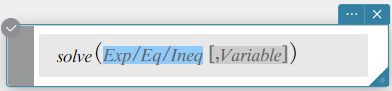
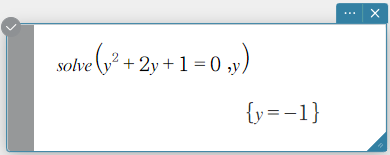
Syntaksi 2: solve(Exp/Eq/Ineq\(≠\), Muuttuja[, arvo, alaraja, yläraja] [ ) ]

• Tämä komento on voimassa vain yhtälöille ja \(≠\) lausekkeille, kun ”arvo” ja seuraavat kohteet sisältyvät siihen. Tässä tapauksessa tämä komento palauttaa likiarvon.
• Aito arvo palautetaan, kun ohitat ”arvo” ja sitä seuraavat kohteet. Jos aitoa arvoa ei voida saada kuitenkaan, likiarvo palautetaan yhtälöihin, jotka perustuvat vain oletukseen, että arvo = 0, alaraja = – ∞, ja yläraja = ∞.

Syntaksi 3: solve({Exp-1/Eq-1, …, Exp-N/Eq-N}, {Muuttuja-1, …, Muuttuja-N} [ ) ]

• Kun ”Exp” on ensimmäinen argumentti, yhtälö Exp = 0 on oletus.

Syntaksi 4:
Ratkaistavan vektoriyhtälön syöttäminen käyttämällä solve( komento sallii 2 kohteen (pisteiden, viivojen, tasojen tai pallojen) välisen suhteen). Tässä 4 tyypillistä syntaksien esimerkkiä on esillä vektoriyhtälön ratkaisemiseksi käyttämällä solve ( komento.

Alla olevissa syntakseissa Vct-1 – Vct-6 ovat sarakevektoreita kolmella (tai kahdella) elementillä, ja s, t, u ja v ovat parametreja.
solve(Vct-1 + s * Vct-2 [= Vct-3, {muuttuja-1}])

• Jos yhtälön oikea puoli (= Vct-3) ohitetaan yllä olevassa syntaksissa, oletetaan että kaikki oikean puolen elementit ovat 0 vektoreita.
  solve(Vct-1 + s * Vct-2 = Vct-3 + t * Vct-4, {muuttuja-1, muuttuja-2})
  solve(Vct-1 + s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5, {muuttuja-1, muuttuja-2, muuttuja-3})
  solve(Vct-1 + s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5 + v * Vct-6, {muuttuja-1, muuttuja-2, muuttuja-3, muuttuja-4})
• Muuttujat (muuttuja 1 – muuttuja 4) voidaan syöttää kunkin vektorin (Vct-1 – Vct-6) elementteihin neljässä yllä olevassa syntaksissa näiden muuttujien ratkaisemiseksi.
  

dSolve

Ratkaisee ensimmäisen, toisen tai kolmannen kertaluvun tavalliset differentiaaliyhtälöt tai ensimmäisen kertaluvun tavallisten differentiaaliyhtälöiden ryhmän.
Syntaksi: dSolve(Eq, riippumaton muuttuja, riippuva muuttuja [, alkuperäinen tila-1, alkuperäinen tila-2][, alkuperäinen tila-3, alkuperäinen tila-4][, alkuperäinen tila-5, alkuperäinen tila-6] [ ) ]
dSolve({Eq-1, Eq-2}, riippumaton muuttuja, {riippuva muuttuja-1, riippuva muuttuja-2} [, alkuperäinen tila-1, alkuperäinen tila-2, alkuperäinen tila-3, alkuperäinen tila-4] [ ) ]

• Jos ohitat alkuperäiset tilat, ratkaisu sisältää satunnaisia vakioita.
• Syötä kaikki alkuperäisten tilojen yhtälöt käyttämällä syntaksia Var = Exp. Kaikki alkuperäiset tilat, jotka käyttävät muuta syntaksia, ohitetaan.

taylor

Löytää Taylorin sarjan lausekkeelle tietyllä muuttujalla.
Syntaksi: taylor (Exp/List, Muuttuja, kertaluku [, keskipiste] [ ) ]

• Nolla on oletus, kun ohitat ”[, keskipisteen]”.

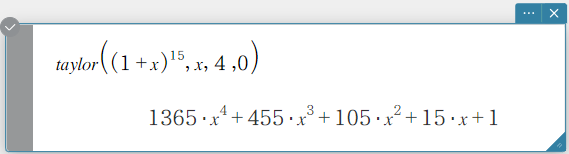
laplace, invLaplace

laplace on Laplace-muunnoksen komento ja invLaplace on käänteisen Laplace-muunnoksen komento.
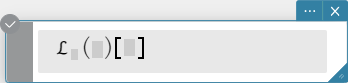
Syntaksi: laplace \(\mathcal{L}_t (f(t))[s]\)
　　\(f(t)\): lauseke
　　\(t\): Muuttuja, jonka suhteen lauseke muunnetaan
　　\(s\): muunnoksen parametri
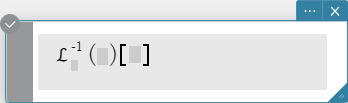
　　　invLaplace \(\mathcal{L}_s^{-1} (L(s))[t]\)
　　\(L(s)\): lauseke
　　\(s\): Muuttuja, jonka suhteen lauseke muunnetaan
　　\(t\): muunnoksen parametri

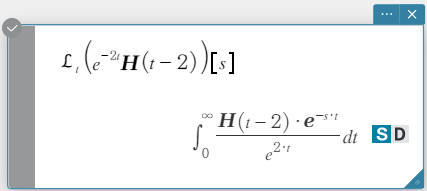
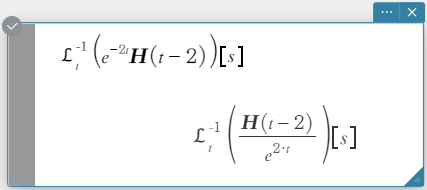
fourier, invFourier

fourier on Fourier-muunnoksen komento ja invFourier on käänteisen Fourier-muunnoksen komento.
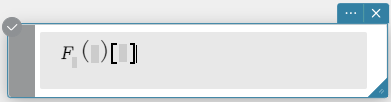
Syntaksi: fourier \(~ Ϝ_x (f(x))[w]\)
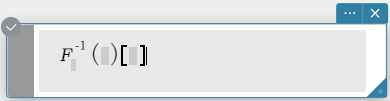
　　invFourier \(~ Ϝ_w^{-1} (f(w))[x]\)
　　\(x\): Muuttuja, jonka suhteen lauseke muunnetaan
　　\(w\): muunnoksen parametri

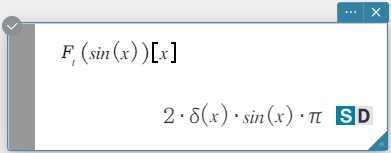
FFT, IFFT

FFT on Fourier-muunnoksen komento ja IFFT on käänteisen nopean Fourier-muunnoksen komento.
FFT:n ja IFT:n suorittamiseen tarvitaan \(2^n\) tietoarvo. FFT ja IFFT lasketaan numeerisesti.
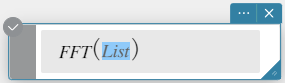
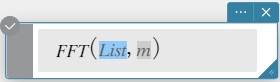
Syntaksi: FFT(list) tai FFT(list, m )
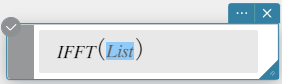
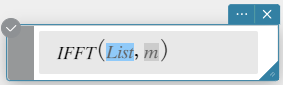
　　IFFT(list) tai IFFT(list, m)

• Tiedon koon on oltava \(2^n\) kohteelle n = 1, 2, 3, …
• Kohteen m arvo on valinnainen. Se voi olla väliltä 0 – 2, ilmaisten käytettävää FFT-parametriä: 0 (Signaalin käsittely), 1 (Puhdas matematiikka), 2 (Tietojen analyysi).