Tilastolliset laskutoimitukset

sisällysluettelo

Tilastolliset peruslaskutoimitukset
Tilastolaskentatietojen arvojen muokkaus
Tietojen arvojen valinta tilastollisia laskutoimituksia varten
Yksimuuttujaisten tilastollisten laskutoimitusten suorittaminen
Regressiokaavion piirtäminen
Histogrammin piirtäminen
Laatikko-jana-kaavion piirtäminen
Ympyräkuvaajan piirtäminen
Sirontakaaviotoiminnot
Yhden otoksen Z-testin suorittaminen
Tilastolliset laskutoimitukset ja kuvaajat

Tilastolliset peruslaskutoimitukset

• Arvojen syöttäminen tilastolaskentatietojen muistilappuun
  Tässä kohdassa näkyvässä esimerkissä alla olevan taulukon arvot syötetään tilastolaskentatietojen muistilapun soluihin A1–B5.

	A	B
1	\(0.5\)	\(-2.1\)
2	\(1.2\)	\(0.3\)
3	\(2.4\)	\(1.5\)
4	\(4.0\)	\(2.0\)
5	\(5.2\)	\(2.4\)

1. Napsauta muistilappuvalikosta kohtaa .
   
   Tämä tuo näkyviin tilastolaskentatietojen muistilapun.
   
   Voit syöttää tietoja soluun A1.
2. Syötä \(0.5\) soluun A1 ja paina sitten [Enter].
   Voit syöttää tietoja soluun A2.
3. Syötä \(1.2\) soluun A2 ja paina sitten [Enter].
   Voit syöttää tietoja soluun A3. Syötä vastaavasti tiedot soluun A5 saakka.
4. Napsauta solua B1.
   Voit syöttää tietoja soluun B1.
5. Syötä \(-2.1\) soluun B1 ja paina sitten [Enter].
   Voit syöttää tietoja soluun B2. Sarake C on myös luotu tässä vaiheessa (ks. alla oleva muistiinpano).
6. Syötä \(0.3\) soluun B2 ja paina sitten [Enter].
   Voit syöttää tietoja soluun B3. Syötä vastaavasti tiedot soluun B5 saakka.
   
   HUOMAUTUS
   Arvon syöttäminen äärimmäisenä oikealla olevaan sarakkeeseen lisää automaattisesti uuden sarakkeen sen oikealle puolelle.
   
   Sarakenimikkeiden (A, B, C,…) alapuolisia soluja voidaan käyttää kunkin sarakkeen luettelon nimeämiseen. Katso lisätietoja kappaleesta ”Luettelon nimeäminen”.

• Tietojen arvojen valinta tilastollisia laskutoimituksia varten

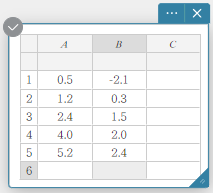
1. Käytä tätä toimintoa kohdan ”Arvojen syöttäminen tilastolaskentatietojen muistilappuun” mukaisesti datan arvojen syöttämiseen.
   

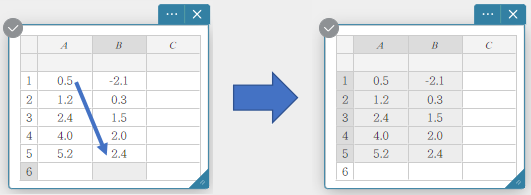
   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)

2. Raahaa solusta A1 soluun B5 tietokoneen hiirellä.
   Näin valitset solualueet solusta A1 soluun B5.
   
   HUOMAUTUS
   Voit valita koko sarakkeen napsauttamalla sarakkeen numeroa.
   Voit valita koko rivin napsauttamalla rivin numeroa.
   Voit napsauttaa tai vetää sarakkeiden numeroita ja käyttää sarakkeiden tietoja kuvaajan piirtämiseen.
   Tässä tapauksessa kuvaajan piirtämisen jälkeen voit myös käyttää kuvaajan muistilapun pudotusvalikkoa valitaksesi muita sarakenumeroita ja piirtääksesi kuvaajan uudelleen.
   

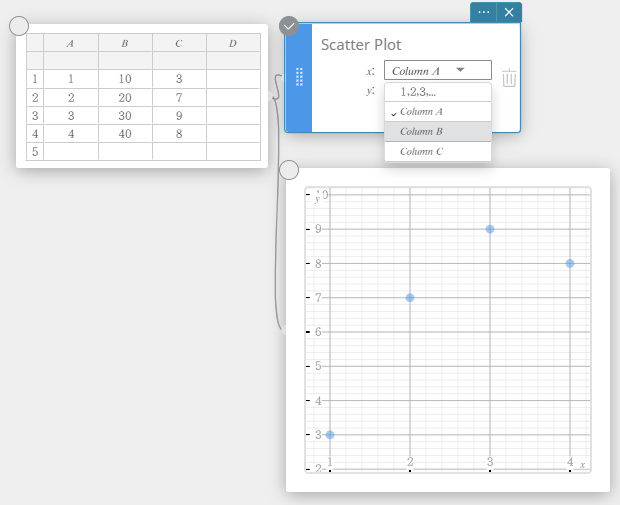
• Tilastollisten laskutoimitusten suorittaminen

Tässä esimerkissä suoritamme kaksimuuttujaisen tilastolaskennan laskutoimitukset ja piirrämme sirontakaavion ja lineaarisen regression kuvaajan.

1. Syötä alla olevan taulukon tietoarvot ja valitse sitten kaikki tiedot.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)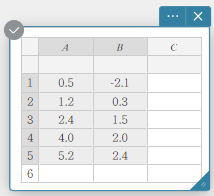

   

2. Napsauta näyttönäppäimistössä [Laskenta] – [Kaksimuuttujainen].
   
   Tämä näyttää kaksimuuttujaisen tilastollisen laskutoimituksen tulokset.
   
3. Napsauta näyttönäppäimistössä.
   
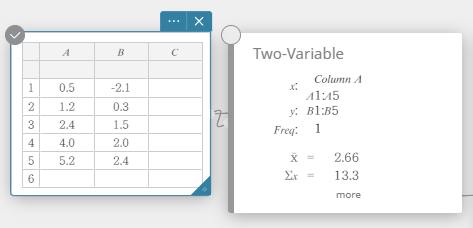
4. Napsauta näyttönäppäimistössä [Kuvaaja] – [Sirontakaavio].
   
   Tämä luo sirontakaavion muistilapun ja piirtää sirontakaavion samanaikaisesti kuvaajan muistilappuun.
   
5. Napsauta näyttönäppäimistössä.
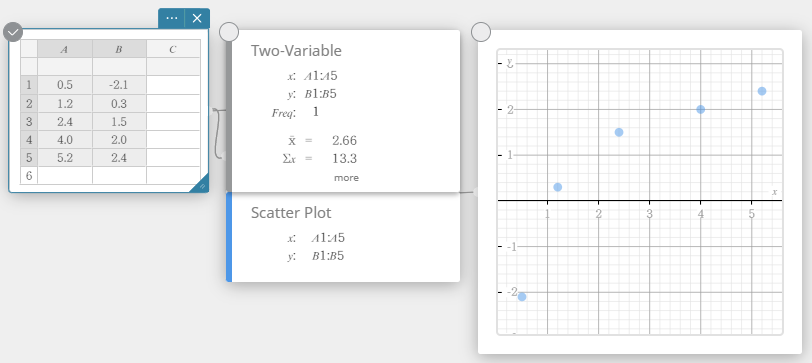
6. Napsauta näyttönäppäimistössä [Regressio] – [Lineaarinen regressio].
   
   Tämä luo lineaarisen regression muistilapun ja piirtää lineaarisen regression kuvaajan samanaikaisesti kuvaajan muistilappuun.
   

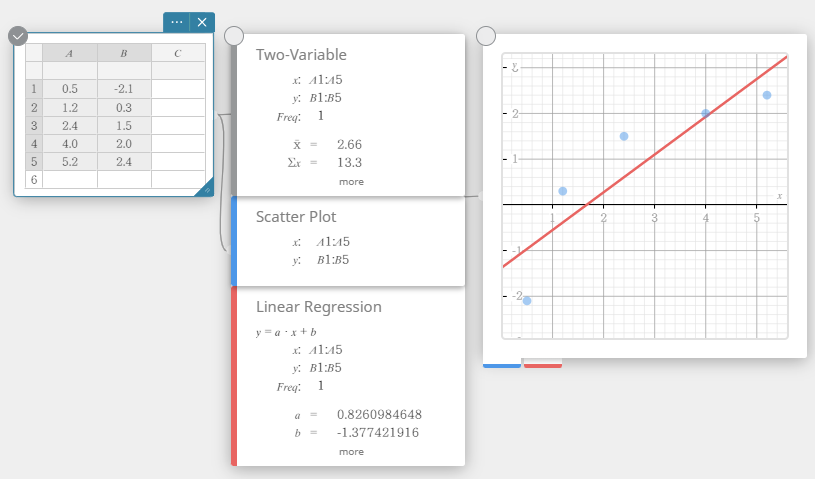
Tilastolaskentatietojen arvojen muokkaus

• Tietoarvojen korjaaminen

1. Napsauta solua, joka sisältää data-arvon, jota haluat korjata.
   
2. Syötä uusi data-arvo ja paina sen jälkeen [Enter].
   

• Rivin lisääminen

1. Napsauta hiiren oikealla painikkeella riviä, johon haluat lisätä uuden rivin.
   Tämä tuo näkyviin valikon.
   
2. Napsauta [Lisää].
   Tämä lisää rivin.
   

• Pylvään lisääminen

1. Napsauta hiiren oikealla painikkeella sarakkeen otsikkoa, johon haluat lisätä uuden sarakkeen.
   Tämä tuo näkyviin valikon.
   
2. Napsauta [Lisää].
   Tämä lisää sarakkeen.
   

• Rivin poistaminen

1. Napsauta hiiren oikealla painikkeella rivin numeroa, jonka haluat poistaa.
   Tämä tuo näkyviin valikon.
   
2. Napsauta [Poista].
   Tämä poistaa rivin.
   

• Sarakkeen poistaminen

1. Napsauta hiiren oikealla painikkeella sarakkeen otsikkoa, jonka haluat poistaa.
   Tämä tuo näkyviin valikon.
   
2. Napsauta [Poista].
   Tämä poistaa sarakkeen.
   

• Luettelon nimeäminen

Kun annat luettelolle nimen, voit käyttää nimeä testeissä ja muissa tilastollisissa laskutoimituksissa. Luetteloiden nimet syötetään sarakkeiden nimien alla oleviin soluihin.

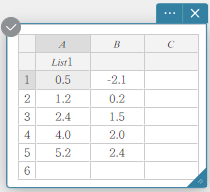
Esimerkki: Nimen ”List1” antaminen sarakkeelle A

1. Kaksoisnapsauta A:n alla olevaa solua.
   Tämä valitsee solun, jotta luettelon nimen voi syöttää.
   
2. Syötä luettelon nimi ”List1” ja paina [Enter].
   Tämä nimeää sarakkeen A luettelon nimeksi ”List1”.
   
   HUOMAUTUS
   Seuraavat säännöt koskevat luetteloiden nimiä.
   － Luetteloiden nimet voivat olla enintään 8 tavun pituisia.
   － Seuraavat kirjaimet on sallittu luettelon nimessä: Isot ja pienet kirjaimet, alaindeksit, numerot.
   － Listan nimet ovat merkkikokoriippuvaisia. Esimerkiksi kukin seuraavista käsitellään eri listan niminä: abc, Abc, aBc, ABC.

Tietojen arvojen valinta tilastollisia laskutoimituksia varten

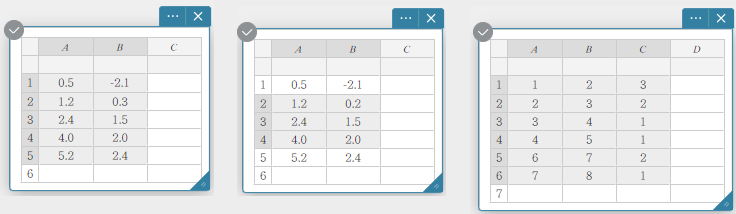
Voit valita solualueen valitsemalla haluamasi solut hiirellä.

Esimerkkejä tietojen valinnasta

HUOMAUTUS
Voit valita koko sarakkeen napsauttamalla sarakkeen numeroa.
Voit valita koko rivin napsauttamalla rivin numeroa.

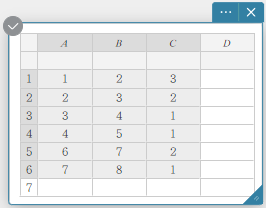
Tilastollisia laskutoimituksia voidaan suorittaa, jos valittujen solujen joukossa on yksi tai useampi tyhjä solu.
Tilastollisiin laskutoimituksiin voi käyttää enintään kolmea saraketta. Tilastollisia laskutoimituksia ei voida suorittaa, jos enemmän kuin kolme saraketta on valittu.

Yksimuuttujaisten tilastollisten laskutoimitusten suorittaminen

1. Syötä alla olevan taulukon tietoarvot, joista tiedot sarakkeeseen A ja frekvenssi sarakkeeseen B.
   

   Tiedot	Frekvenssi
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Raahaa solusta A1 soluun B5 valitaksesi niiden väliset solualueet.
   

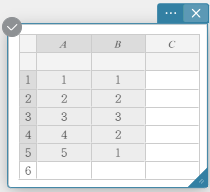
3. Napsauta näyttönäppäimistössä [Laskenta] – [Yksi muuttuja].
   Tämä näyttää yksimuuttujaisen tilastollisen laskutoimituksen tulokset.
   
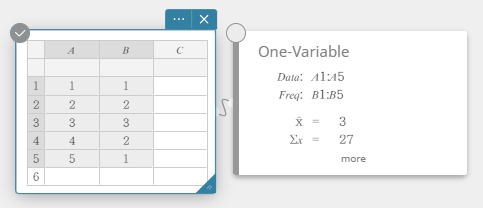
4. Näytä muut piilotetut laskutoimitusten tuloskohteet napsauttamalla [lisää] tilastollisten laskutoimitusten muistilapussa.
   Tämä näyttää piilotetut laskutoimituksen tulokset.
   Palauta tilastollisten laskutoimitusten muistilappu pienennetyn koon konfiguraatioon napsauttamalla [Piilota].
   

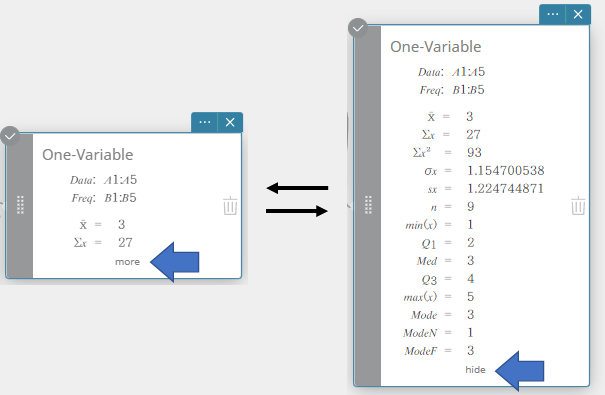
Kun suoritat yksimuuttujaisen tilastollisen laskutoimituksen, tulokset näkyvät alla.
\(\bar{\rm x}\)　　　otoskeskiarvo
\(\Sigma {\rm x}\)　　 tietojen summa
\(\Sigma {\rm x}^2\)　　 neliösumma
\(\sigma {\rm x}\)　　　perusjoukon standardipoikkeama
\({\rm sx}\)　　　 otoksen standardipoikkeama
\({\rm n}\)　　　　otoskoko
\({\rm min(x)}\)　minimi
\({\rm Q}_1\)　　　ensimmäinen kvartiili
\({\rm Med}\)　　 mediaani
\({\rm Q}_3\)　　　 kolmas kvartiili
\({\rm max(x)}\)　maksimi
\({\rm Mode}\)　　moodi
\({\rm ModeN}\)　 moodin lukumäärä
\({\rm ModeF}\)　moodin frekvenssi
When \({\rm Mode}\):lla on useita ratkaisuja, ne kaikki näytetään.

Regressiokaavion piirtäminen

Tässä esimerkissä käytämme alla olevia tietoarvoja sirontakaavion, lineaarisen regression kuvaajan ja 2. asteen regression kuvaajan piirtämiseen.

1. Syötä alla olevan taulukon tietoarvot ja valitse sitten kaikki tiedot.
   

   A	B
   \(1.0\)	\(1.0\)
   \(1.2\)	\(1.1\)
   \(1.5\)	\(1.2\)
   \(1.6\)	\(1.3\)
   \(1.9\)	\(1.4\)
   \(2.1\)	\(1.5\)
   \(2.4\)	\(1.6\)
   \(2.5\)	\(1.7\)
   \(2.7\)	\(1.8\)
   \(3.0\)	\(2.0\)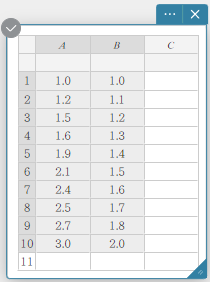

   

2. Napsauta näyttönäppäimistössä [Kuvaaja] – [Sirontakaavio].
   
   Tämä luo sirontakaavion muistilapun ja piirtää sirontakaavion samanaikaisesti kuvaajan muistilappuun.
   
3. Napsauta näyttönäppäimistössä.
   
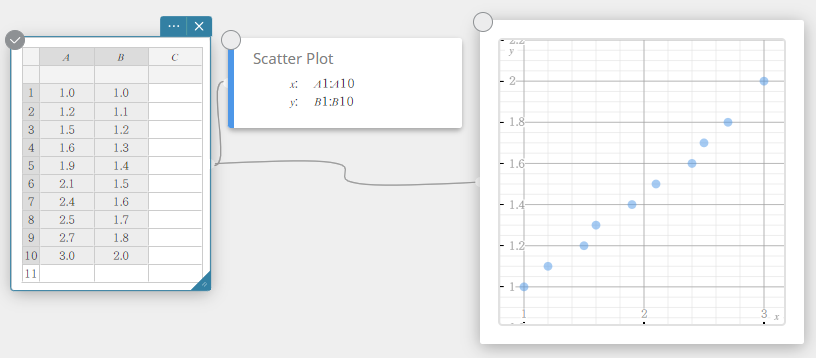
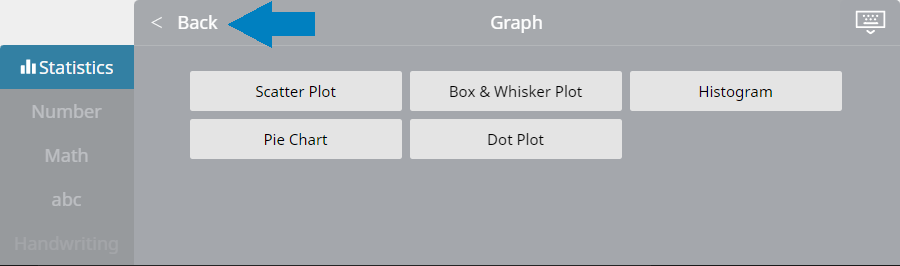
4. Napsauta näyttönäppäimistössä [Regressio] – [Lineaarinen regressio].
   
   Tämä luo lineaarisen regression muistilapun ja piirtää lineaarisen regression kuvaajan samanaikaisesti kuvaajan muistilappuun.
   
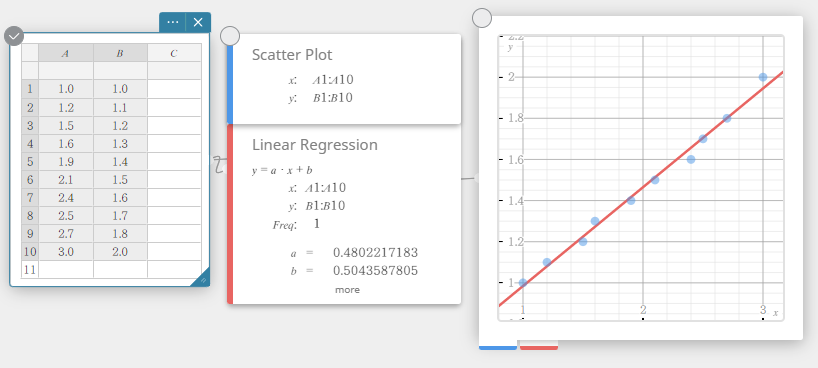
5. Napsauta näyttönäppäimistössä [2. asteen regressio].
   
   Tämä luo 2. asteen regression muistilapun ja piirtää 2. asteen regression kuvaajan samanaikaisesti kuvaajan muistilappuun.
   

Histogrammin piirtäminen

1. Syötä alla olevan taulukon tietoarvot, joista tiedot sarakkeeseen A ja frekvenssi sarakkeeseen B.
   

   Tiedot	Frekvenssi
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Raahaa solusta A1 soluun B5 valitaksesi niiden väliset solualueet.
   

3. Napsauta näyttönäppäimistössä [Kuvaaja] – [Histogrammi].
   Tämä luo histogrammin muistilapun ja piirtää histogrammin samanaikaisesti kuvaajan muistilappuun.
   
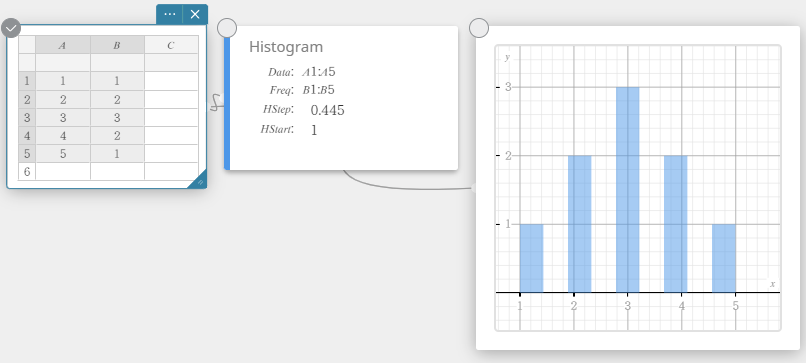
   HUOMAUTUS
   Voit halutessasi muuttaa histogrammin piirroksen aloitusarvoa (HStart) ja askelarvoa (HStep). Napsauta histogrammin muistilapussa HStart tai HStep, ja syötä sitten haluamasi arvo.
   

Laatikko-jana-kaavion piirtäminen

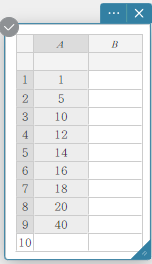
1. Syötä alla olevan taulukon tietoarvot sarakkeeseen A.
   

   A
   \(1\)
   \(5\)
   \(10\)
   \(12\)
   \(14\)
   \(16\)
   \(18\)
   \(20\)
   \(40\)

2. Raahaa solusta A1 soluun A9 valitaksesi niiden väliset solualueet.
   

3. Napsauta näyttönäppäimistössä [Kuvaaja] – [Laatikko-jana-piirros].
   Tämä luo laatikko-jana-piirroksen muistilapun ja piirtää samanaikaisesti laatikko-jana-piirroksen kuvaajan muistilappuun.
   
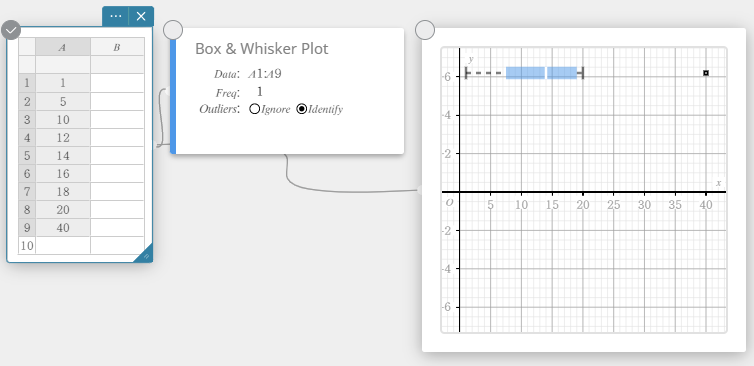
   HUOMAUTUS
   Voit halutessasi tuoda näyttöön poikkeavat arvot. Tee se valitsemalla [Tunnista] laatikko-jana-piirroksen muistilapun Poikkeavat arvot -kohdassa.
   

Ympyräkuvaajan piirtäminen

1. Syötä alla olevan taulukon tietoarvot sarakkeeseen A.
   

   A
   \(5\)
   \(10\)
   \(20\)
   \(30\)
   \(40\)

2. Raahaa solusta A1 soluun A5 valitaksesi niiden väliset solualueet.
   

3. Napsauta näyttönäppäimistössä [Kuvaaja] – [Ympyrädiagrammi].
   Tämä luo ympyrädiagrammin muistilapun ja piirtää ympyrädiagrammin kuvaajan erilliselle muistilapulle samanaikaisesti*.
   
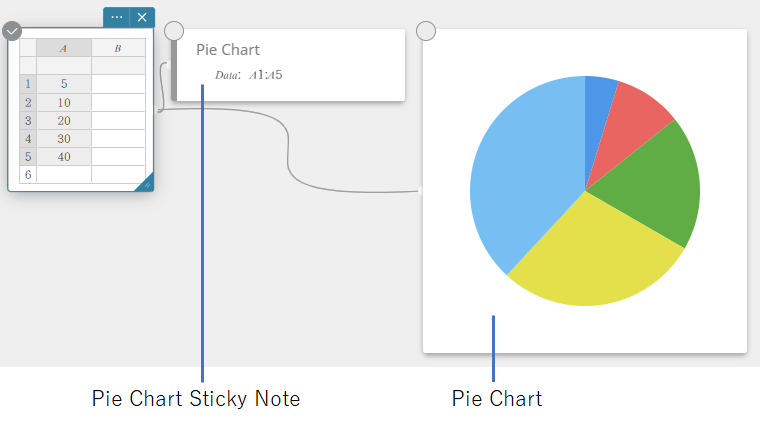
   *　Tämä piirtää kuvaajan kuvaajan muistilapulle. Muistilapun tyyppi on erilainen, kun ympyräkuvaaja piirretään muistilapulle.

Sirontakaaviotoiminnot

• Sirontakaavion pisteiden liikuttaminen

1. Syötä alla olevan taulukon tietoarvot sarakkeisiin A ja B.
   

   Tiedot	Frekvenssi
   \(0.5\)	\(-2.1\)
   \(1.2\)	\(0.3\)
   \(2.4\)	\(1.5\)
   \(4.0\)	\(2.0\)
   \(5.2\)	\(2.4\)

2. Raahaa solusta A1 soluun B5 valitaksesi niiden väliset solualueet.
   

3. Napsauta näyttönäppäimistössä [Kuvaaja] – [Sirontakaavio].
   Tämä luo sirontakaavion muistilapun ja kuvaajan muistilapun ja piirtää sirontakaavion kuvaajan muistilappuun.
   
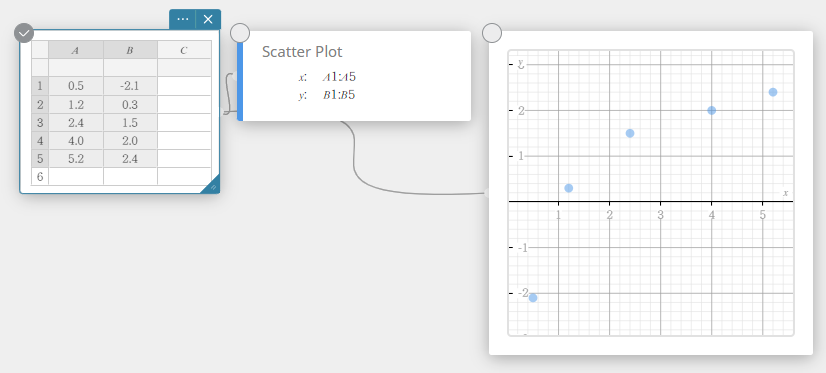
4. Liikuta sirontakaavion pistettä raahaamalla.
   Tämä muuttaa myös tilastolaskentatietojen muistilapun arvot kohteen koordinaatteihin.
   

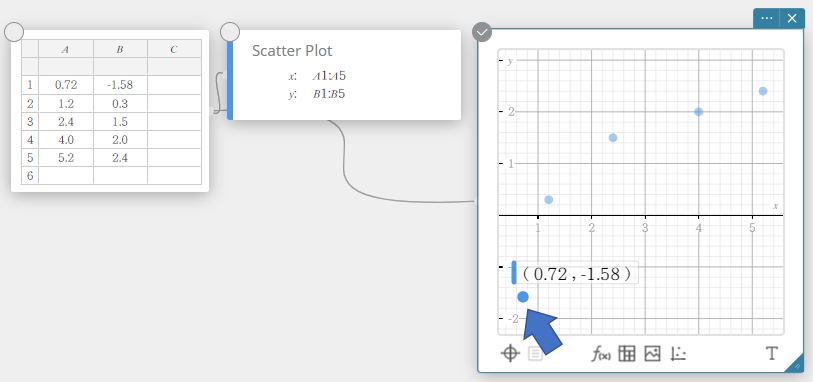
• Solun lukitseminen

HUOMAUTUS
Kun solu on lukittu, sen tietoarvo ei muutu, vaikka yrität liikuttaa sen sirontakaavion pistettä. Jos esimerkiksi lukitset sarakkeen A solun, vastaavaa sirontakaavion pistettä ei voi liikuttaa x-akselissa.

1. Jatka menetelmästä kohdassa ”Sirontakaavion pisteiden liikuttaminen” valitsemalla solu A1.
2. Napsauta tilastollisten laskutoimituksen muistilapussa.
   
3. Napsauta -kuvaketta kohdan [Lukitse] vieressä.
   Tämä lukitsee solut A1. Jos raahaat sirontakaavion pisteen, joka vastaa soluja A1 ja B1, liikuttaminen ei ole mahdollista x-akselilla.
   

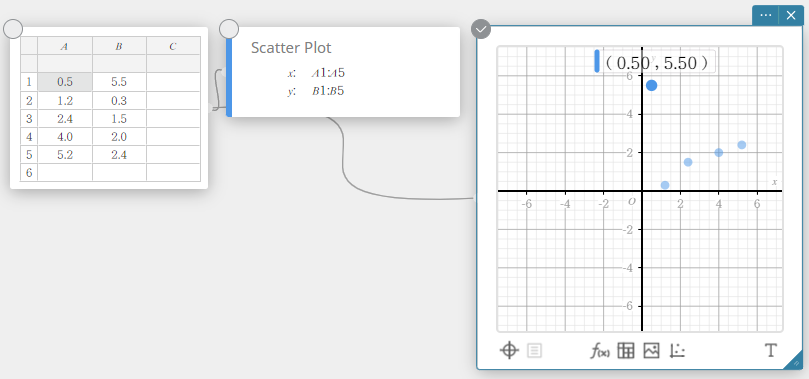
• Solun lukituksen poistaminen

1. Valitse lukittu solu, jonka lukituksen haluat poistaa.
2. Napsauta tilastollisten laskutoimituksen muistilapussa.
   
3. Napsauta -kuvaketta kohdan [Poista lukitus] vieressä.

Yhden otoksen Z-testin suorittaminen

• Määritellään tieto-otosten määrä ja suoritetaan yhden otoksen Z-testi

Esimerkki:
Otoskoko: \(n=48\)
Otoskeskiarvo: \(\overline{x}=24.5\)
Nollahypoteesi: \(\mu \ne 0\)
Standardipoikkeama: \(\sigma=3\)

1. Luo tilastolaskentatietojen muistilappu.
2. Napsauta näyttönäppäimistössä [Testi] – [Yhden otoksen Z-testi].
   
   Tämä luo yhden otoksen Z-testin muistilapun.
   
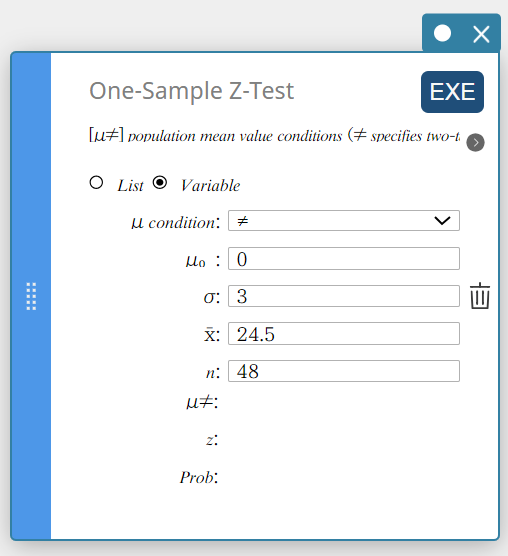
3. Tee asetukset alla olevan mukaisesti.
   \(\mu\) condition: Valitse ”\(\ne\)” esiin tulevasta valikosta.
   \(\mu_0\) : Syötä \(0\).
   \(\sigma\): Syötä \(3\).
   \(\overline{x}\) : Syötä \(24.5\).
   \(n\) : Syötä \(48\).
   
4. Napsauta [EXE].
   
   Tämä näyttää laskentatulokset ja kuvaajan.
   
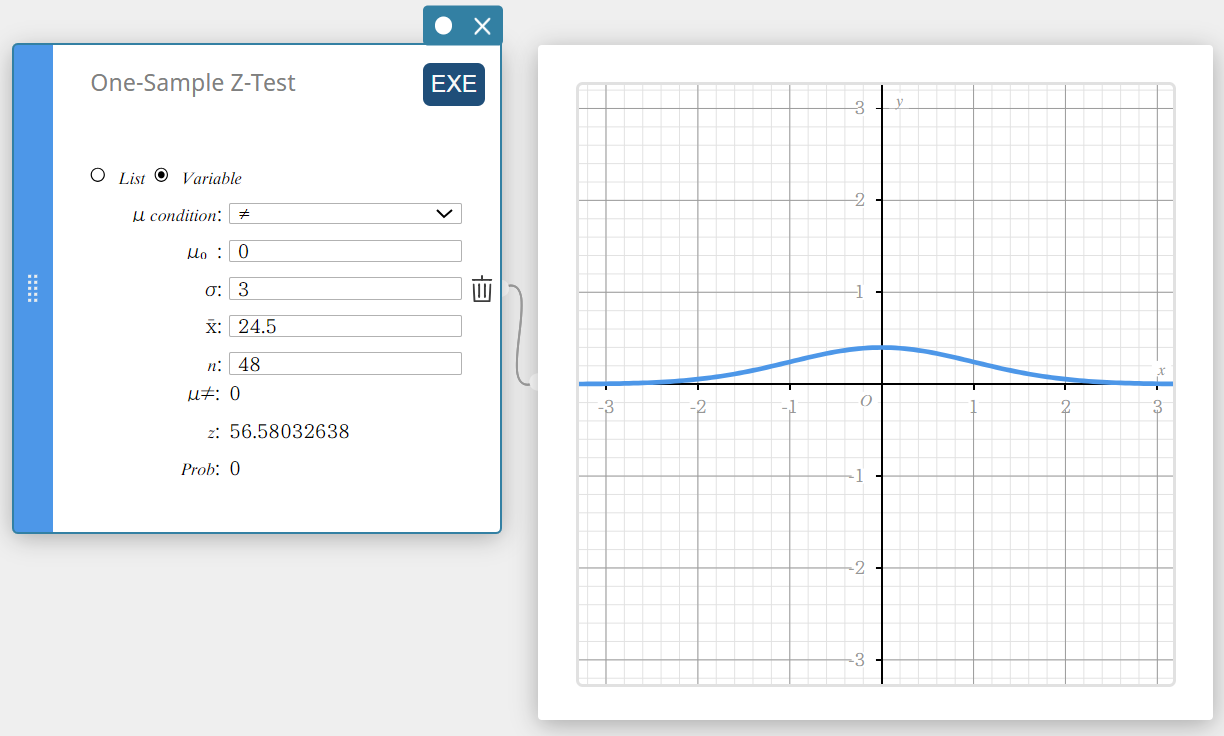
   \(\mu \ne\) perusjoukon keskiarvon ehto
   \(\rm z\) 　　\(\rm z\)-arvo
   Prob 　\(\rm p\)-arvo
   \(\overline{x}\) 　　otoskeskiarvo
   \(n\) 　　otoskoko

• Luetteloiden käyttäminen yhden otoksen Z-testin suorittamiseen

1. Syötä seuraava listan nimet: List 1 sarakkeeseen A, List 2 sarakkeeseen B.
2. Syötä tietoarvo alla olevaan taulukkoon.
   
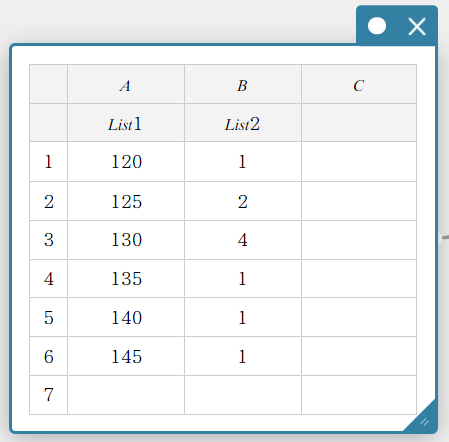
3. Vedä solusta A1 soluun B6 valitaksesi niiden väliset solualueet.
4. Napsauta näyttönäppäimistössä [Testi] – [Yhden otoksen Z-testi].
   
   Tämä luo yhden otoksen Z-testin muistilapun.
   
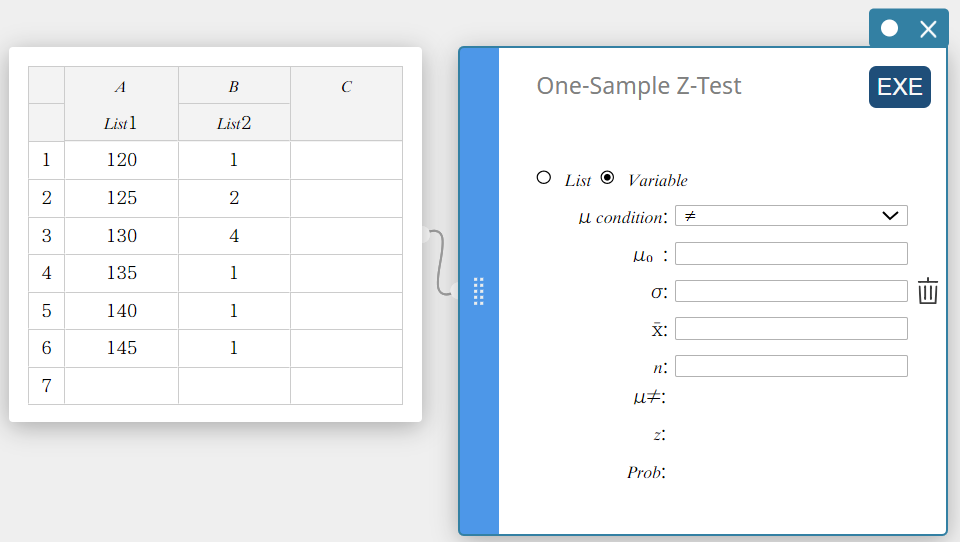
5. Napsauta ”List”.
   
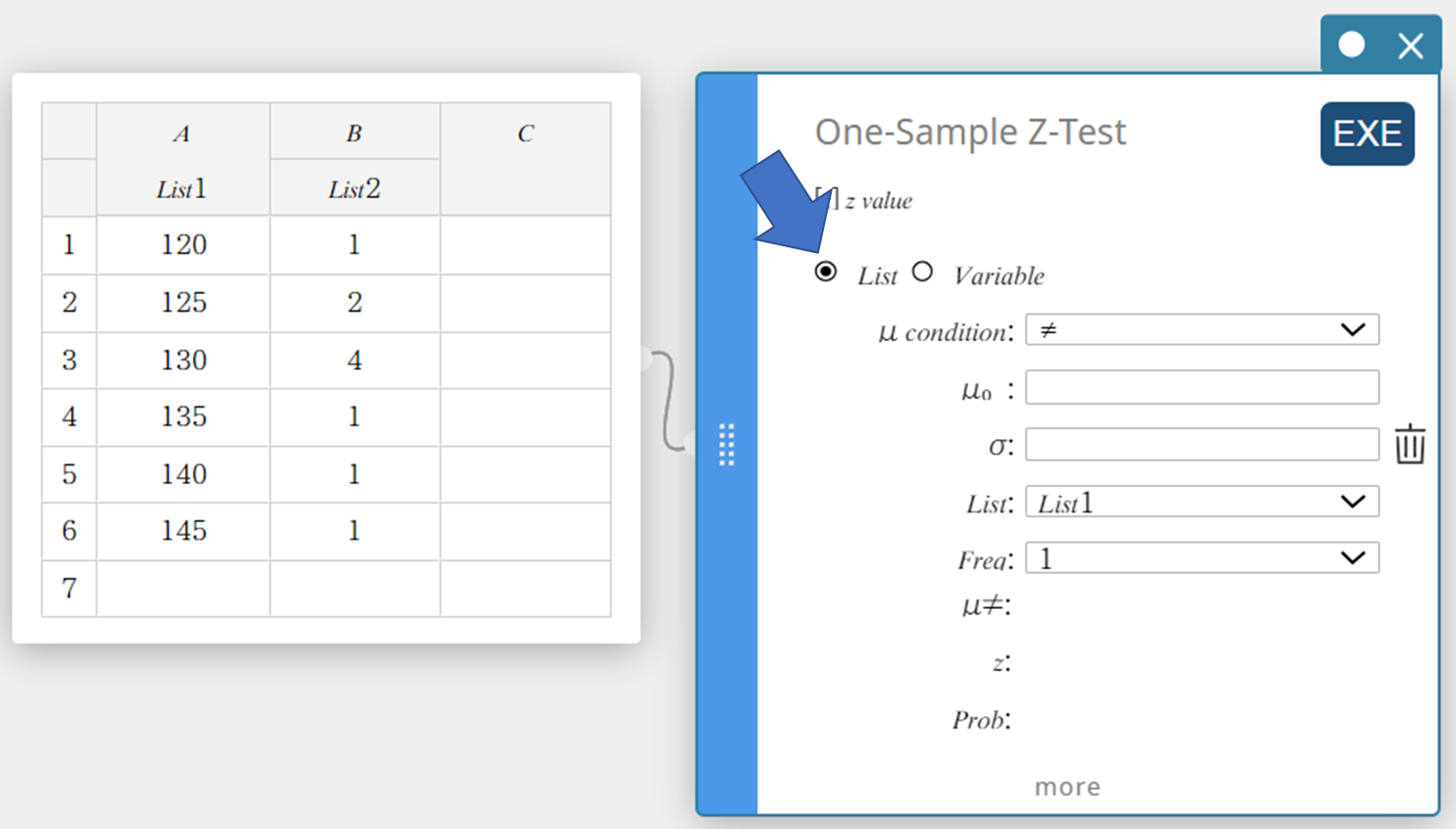
6. Tee asetukset alla olevan mukaisesti.
   \(\mu\) condition: Valitse ”\(\gt\)” esiin tulevasta valikosta.
   \(\mu_0\) : Syötä \(120\).
   \(\sigma\): Syötä \(19\).
   List: Valitse esiin tulevasta valikosta ”List1”.
   Frekvenssi: Valitse esiin tulevasta valikosta ”List2”.
   
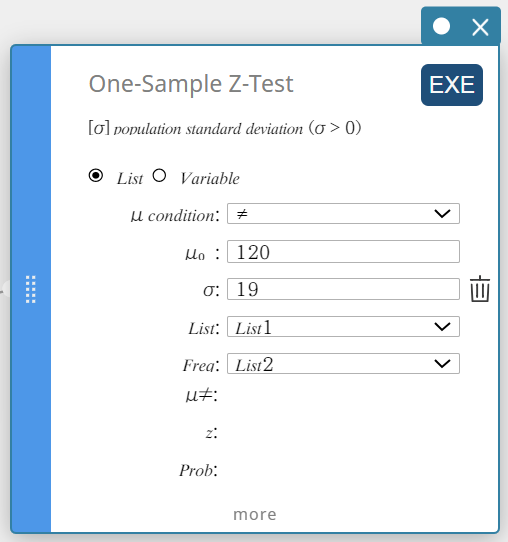
7. Napsauta [EXE].
   
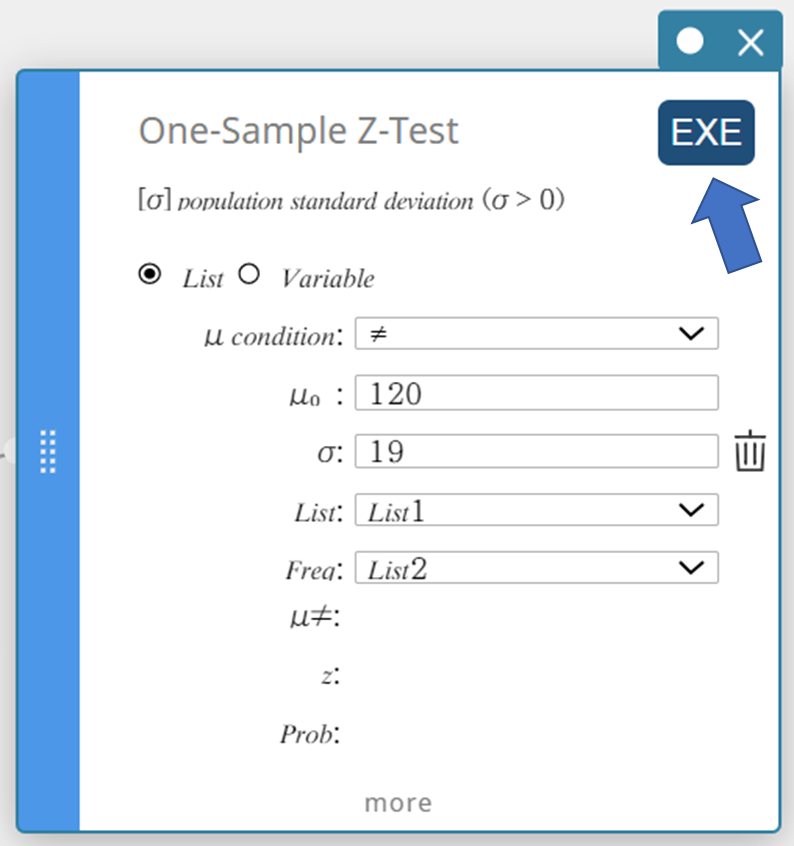
   Tämä näyttää laskentatulokset ja kuvaajan.
   
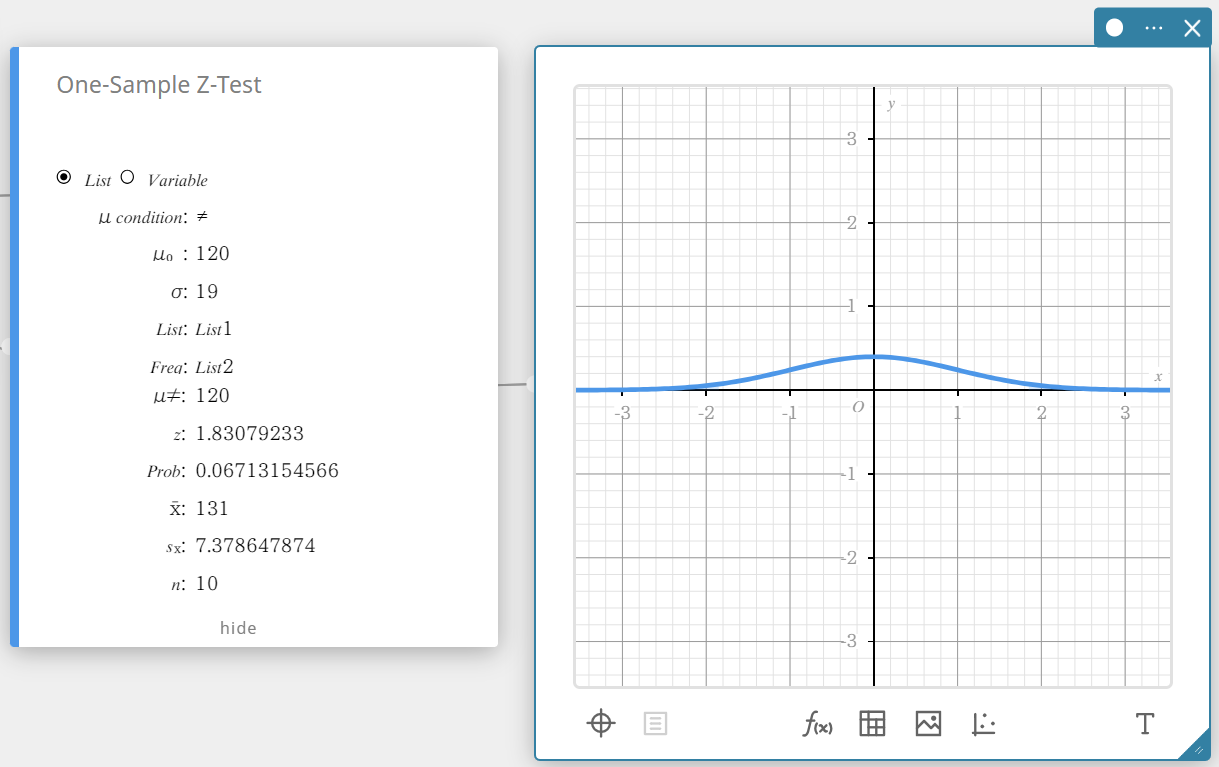
   \(\mu \gt\)　perusjoukon keskiarvon ehto
   \(\rm z\)　　　\(\rm z\)-arvo
   Prob　　\(\rm p\)-arvo
   \(\overline{x}\)　　　otoskeskiarvo
   \({\rm Sx}\)　　otoksen standardipoikkeama
   \(n\)　　　otoskoko

Tilastolliset laskutoimitukset ja kuvaajat

Tilastolliset laskutoimitukset

Yksimuuttujainen
Tämä näyttää yksimuuttujaisen tilastolaskennan laskentatulokset.

\(\bar{\rm x}\) … otoskeskiarvo
\(\Sigma {\rm x}\) … tietojen summa
\(\Sigma {\rm x}^2\) … neliösumma
\(\sigma {\rm x}\) … perusjoukon standardipoikkeama
\({\rm sx}\) … otoksen standardipoikkeama
\({\rm n}\) … otoskoko
\({\rm min(x)}\) … minimi
\({\rm Q}_1\) … ensimmäinen kvartiili
\({\rm Med}\) … mediaani
\({\rm Q}_3\) … kolmas kvartiili
\({\rm max(x)}\) … maksimi
\({\rm Mode}\) … moodi
\({\rm ModeN}\) … moodin lukumäärä
\({\rm ModeF}\) … moodin frekvenssi

Kun \({\rm Mode}\):lla on useita ratkaisuja, ne kaikki näytetään.

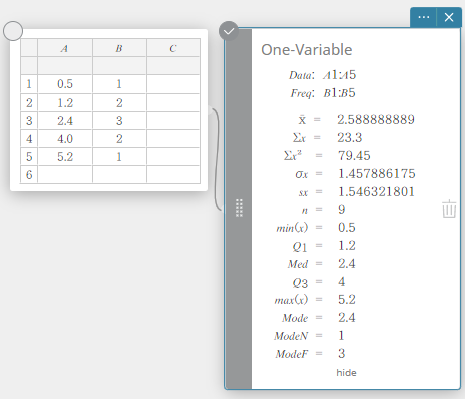
Kaksimuuttujainen
Tämä näyttää riippuvan muuttujan tilastolaskennan laskentatulokset.

\(\bar{\rm x}\) … otoskeskiarvo
\(\Sigma {\rm x}\) … tietojen summa
\(\Sigma {\rm x}^2\) … neliösumma
\(\sigma {\rm x}\) … perusjoukon standardipoikkeama
\({\rm sx}\) … otoksen standardipoikkeama
\({\rm n}\) … otoskoko
\(\bar{\rm y}\) … otoskeskiarvo
\(\Sigma {\rm y}\) … tietojen summa
\(\Sigma {\rm y}^2\) … neliösumma
\(\sigma {\rm y}\) … perusjoukon standardipoikkeama
\({\rm sy}\) … otoksen standardipoikkeama
\(\Sigma {\rm xy}\) … XList- ja YList-tietojen tulojen summa
\({\rm minX}\) … minimi
\({\rm maxX}\) … maksimi
\({\rm minY}\)… minimi
\({\rm maxY}\) … maksimi

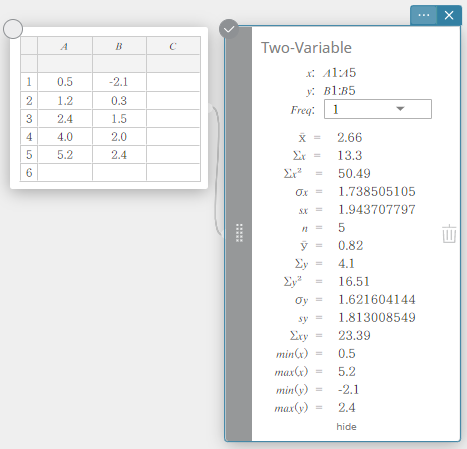
Regressiolaskutoimitukset ja kuvaajat

Lineaarinen regressio
Lineaarinen regressio käyttää pienimmän neliösumman menetelmää määrittääkseen yhtälön, joka sopii parhaiten tietopisteillesi, ja palauttaa arvot kaltevuudelle ja y-leikkauspisteelle. Tämän suhteen graafinen esitysmuoto on lineaarisen regression kuvaaja.

\(y = a \cdot x + b\)
\(a\) … regressiokerroin (kaltevuus)
\(b\) … regression vakiotermi (y-leikkauspiste)
\(r\) … korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

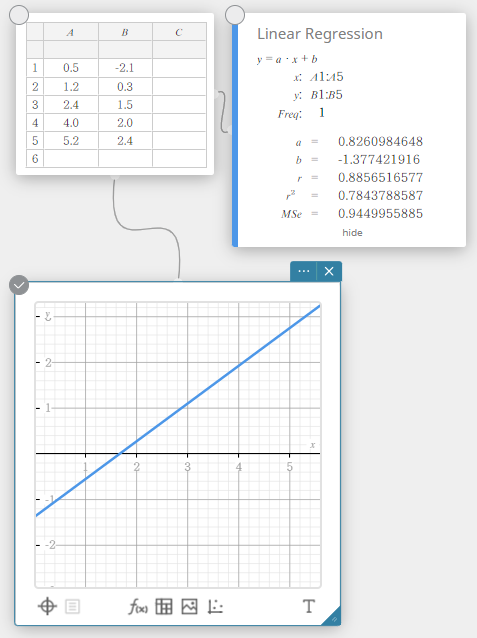
Med-Med-regressio
Kun epäilet, että tiedot sisältävät äärimmäisiä arvoja, voit käyttää Med-Med-kuvaajaa (joka perustuu mediaaneihin) lineaarisen regression kuvaajan sijaan. MedMed-kuvaaja muistuttaa lineaarisen regression kuvaajaa, mutta se myös minimoi äärimmäisten arvojen vaikutuksia.

\(y = a \cdot x + b\)
\(a\) … regressiokerroin (kaltevuus)
\(b\) … regression vakiotermi (y-leikkauspiste)

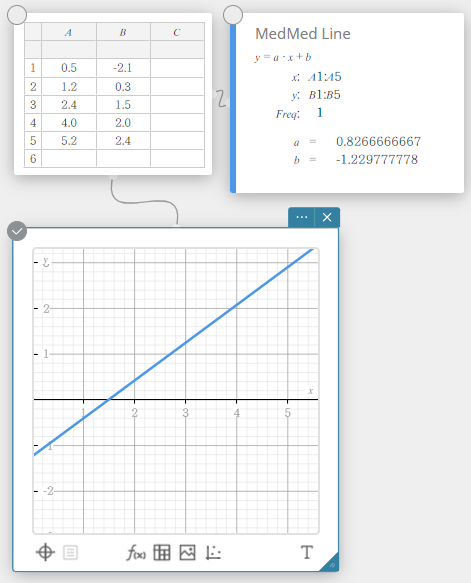
2. asteen regressio
2. asteen regression kuvaaja käyttää pienimmän neliösumman tapaa piirtääkseen käyrän, joka kulkee mahdollisimman monen tietopisteen läheisyydestä. Tämä kuvaaja voidaan ilmaista 2. asteen regressiolausekkeena.

\(y = a \cdot x^2 + b \cdot x + c\)
\(a\) … regression toinen kerroin
\(b\) … regression ensimmäinen kerroin
\(c\) … regression vakiotermi (y-leikkauspiste)
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

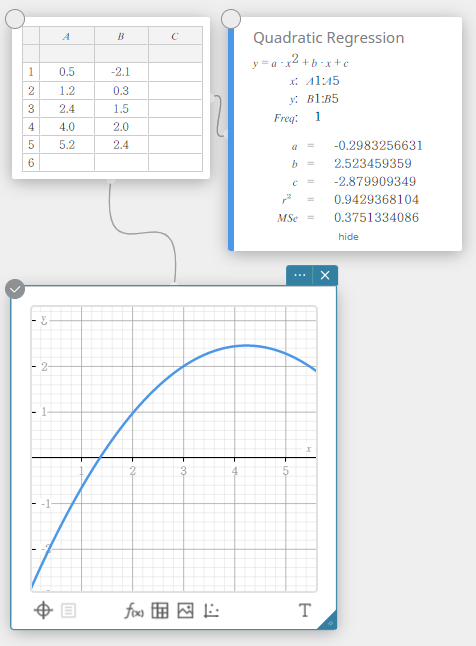
3. asteen regressio
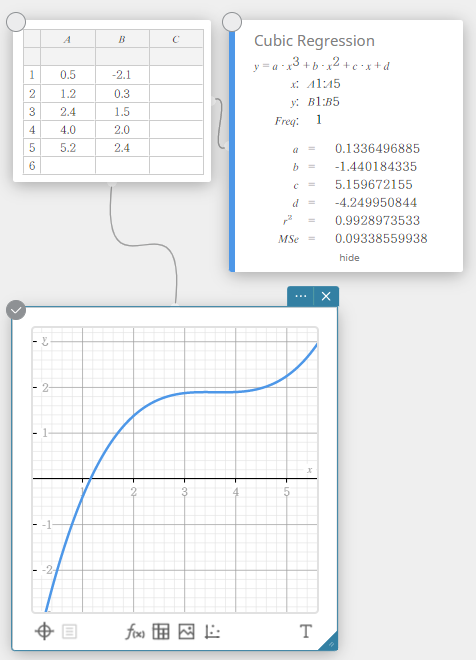
3. asteen regression kuvaaja käyttää pienimmän neliösumman tapaa piirtääkseen käyrän, joka kulkee mahdollisimman monen tietopisteen läheisyydestä. Tämä kuvaaja voidaan ilmaista 3. asteen regressiolausekkeena.

\(y = a \cdot x^3 + b \cdot x^2 + c \cdot x + d\)
\(a\) … regression kolmas kerroin
\(b\) … regression toinen kerroin
\(c\) … regression ensimmäinen kerroin
\(d\) … regression vakiotermi (y-leikkauspiste)
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

4. asteen regressio
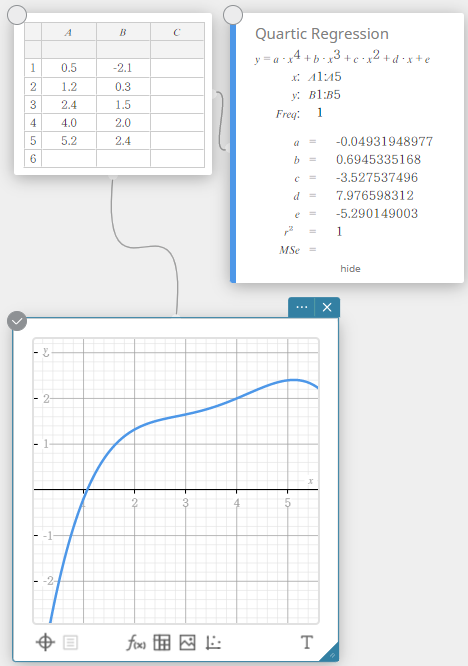
4. asteen regression kuvaaja käyttää pienimmän neliösumman tapaa piirtääkseen käyrän, joka kulkee mahdollisimman monen tietopisteen läheisyydestä. Tämä kuvaaja voidaan ilmaista 4. asteen regressiolausekkeena.

\(y = a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e\)
\(a\) … regression neljäs kerroin
\(b\) … regression kolmas kerroin
\(c\) … regression toinen kerroin
\(d\) … regression ensimmäinen kerroin
\(e\) … regression vakiotermi (y-leikkauspiste)
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

Logaritminen regressio
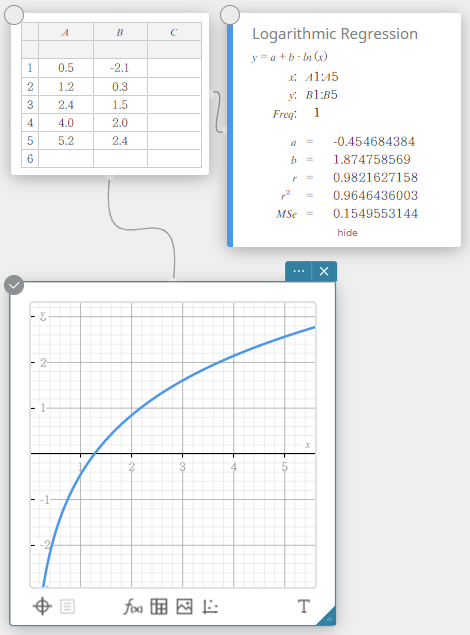
Logaritminen regressio ilmaisee \(y\):n logaritmisena \(x\)-funktiona. Normaali logaritminen regressiokaava on \(y=a+b \cdot \ln(x)\). Jos sanotaan \(X=\ln(x)\), kaavio vastaa lineaarisen regression kaavaa \(y=a+b \cdot X\).

\(y = a + b \cdot \ln(x)\)
\(a\) … regression vakiotermi
\(b\) … regression kerroin
\(r\) … korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

Eksponentiaalinen regressio
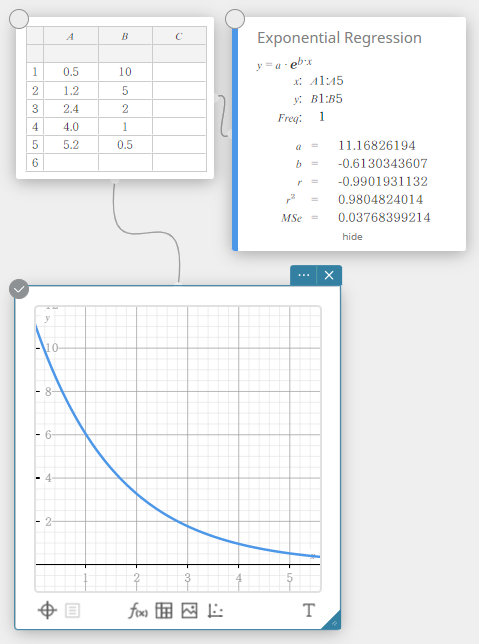
Eksponentiaalista regressiota voidaan käyttää, kun \(y\) on verrannollinen \(x\):n eksponentiaaliseen funktioon. Normaali eksponentiaalinen regressiokaava on \(y=a \cdot e^{b \cdot x}\). Jos otamme molempien sivujen logaritmit, tulos on \(\ln(y)=\ln(a)+b \cdot x\). Jos tämän jälkeen sanotaan, että \(Y=\ln(y)\) ja \(A=\ln(a)\), kaava vastaa lineaarisen regression kaavaa \(Y=A+b \cdot x\).

\(y = a \cdot e^{b \cdot x}\)
\(a\) … regression kerroin
\(b\) … regression vakiotermi
\(r\) … korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

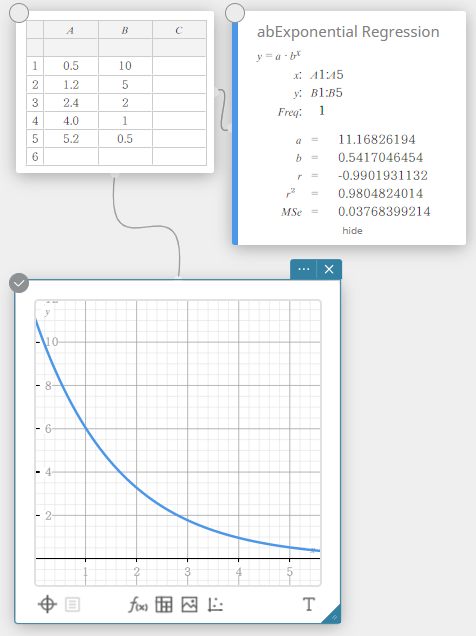
abEksponentiaalinen regressio
Eksponentiaalista regressiota voidaan käyttää, kun \(y\) on verrannollinen \(x\):n eksponentiaaliseen funktioon. Normaali eksponentiaalinen regressiokaava on tässä tapauksessa \(y=a \cdot b^x\). Jos otamme molempien sivujen luonnolliset logaritmit, tulos on \(\ln(y)=\ln(a)+(\ln(b)) \cdot x\). Jos tämän jälkeen sanotaan, että \(Y=\ln(y)\), \(A=\ln(a)\) ja \(B=\ln(b)\), kaava vastaa lineaarisen regression kaavaa \(Y=A+B \cdot x\).

\(y = a \cdot b^x\)
\(a\) … regression vakiotermi
\(b\) … regression kerroin
\(r\) … korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

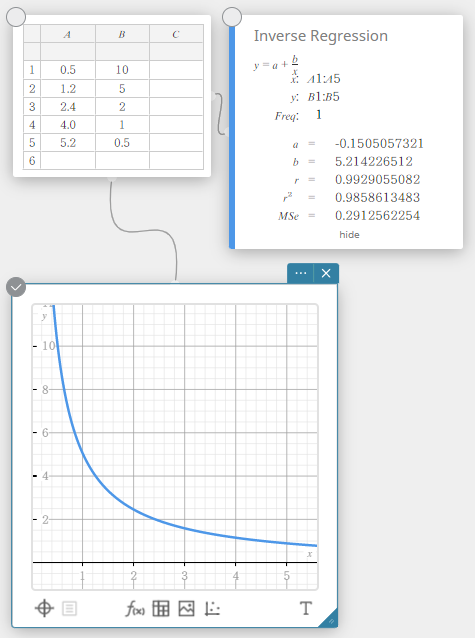
Käänteinen regressio
Käänteinen regressio ilmaisee \(y\):n käänteisenä \(x\)-funktiona. Normaali käänteinen regressiokaava on \(y=a+b/x\). Jos sanotaan \(X=1/x\), kaavio vastaa lineaarisen regression kaavaa \(y=a+b･X\).

\(y=a+b/x\)
\(a\) … regression vakiotermi
\(b\) … regression kerroin
\(r\) …. korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

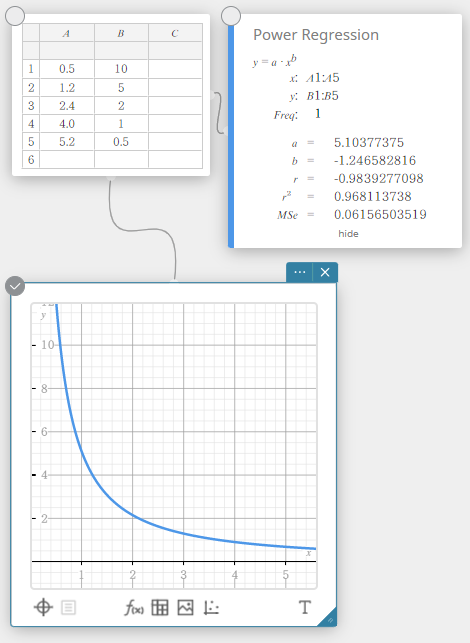
Potenssifunktion regressio
Potenssifunktion regressiota voidaan käyttää, kun \(y\) on verrannollinen \(x\):n potenssifunktioon. Normaali potenssifunktion regressiokaava on \(y=a \cdot x^b\). Jos otamme molempien sivujen luonnolliset logaritmit, tulos on \(\ln(y)=\ln(a)+b \cdot \ln(x)\). Jos tämän jälkeen sanotaan, että \(X=\ln(x)\), \(Y=\ln(y)\), ja \(A=\ln(a)\), kaava vastaa lineaarisen regression kaavaa \(Y=A+b \cdot X\).

\(y = a \cdot x^b\)
\(a\) … regression kerroin
\(b\) … regression potenssifunktio
\(r\) … korrelaatiokerroin
\(r^2\) … selitysaste
\({\rm MSe}\) … keskineliövirhe

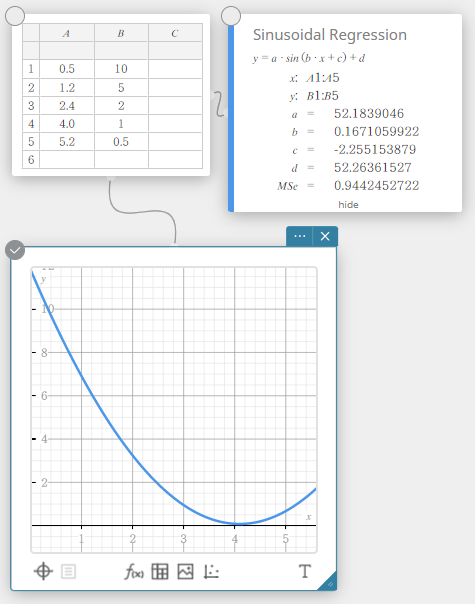
Siniregressio
Siniregressio on paras tiedoille, jotka toistuvat säännöllisesti määritetyllä aikavälillä ajan mittaan.

\(y = a \cdot \sin( b \cdot x + c ) + d\)
\(a\), \(b\), \(c\), \(d\) … regression kerroin
\({\rm MSe}\) … keskineliövirhe

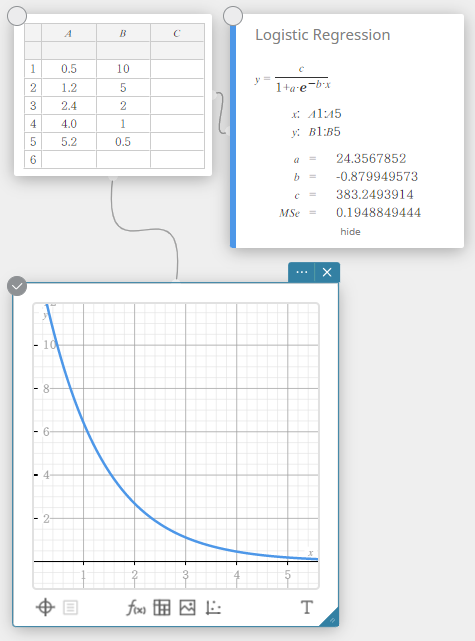
Logistinen regressio
Logistinen regressio on paras tiedoille, joiden arvot kasvavat jatkuvasti ajan mittaan, kunnes kyllästyspiste on saavutettu.

\(\displaystyle y=\frac{c}{1+a \cdot e^{-b \cdot x}}\)
\(a\), \(b\), \(c\) … regression kerroin
\({\rm MSe}\) … keskineliövirhe

Testit

1 otoksen Z-testi
Testaa yhden otoksen keskiarvoa vertaamalla sitä nollahypoteesin tunnettuun keskiarvoon, kun perusjoukon standardipoikkeama tunnetaan. 1 otoksen Z-testissä käytetään normaalijakaumaa.

\(Z=\displaystyle \frac{\overline{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) : otoskeskiarvo
\(\mu_{0}\) : oletettu perusjoukon keskiarvo
\(\sigma\) : perusjoukon standardipoikkeama
\(n\) : otoskoko

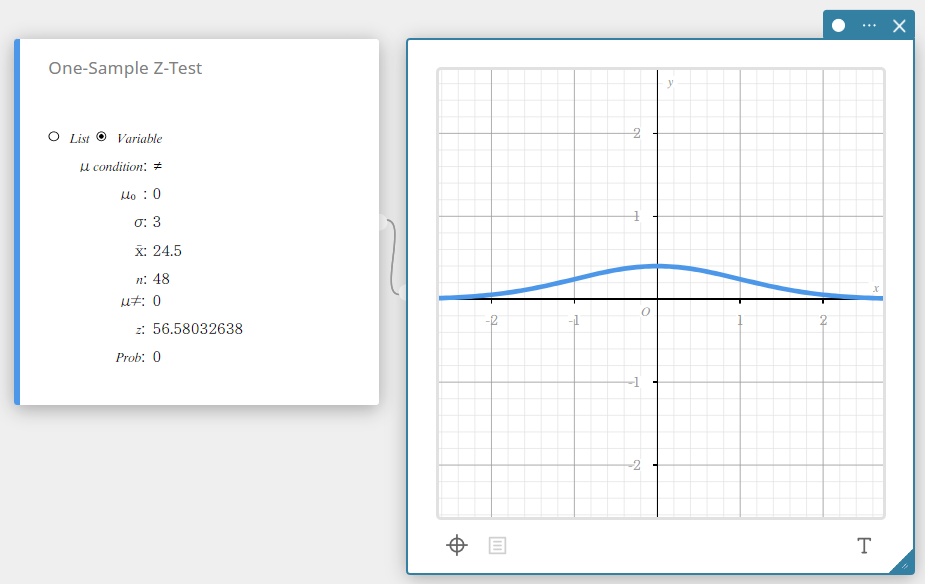
Tietotyyppi: Muuttuja

• Syötettävät termit
  \( \mu \) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  \( \mu_{0} \) : oletettu perusjoukon keskiarvo
  \( \sigma \) : perusjoukon standardipoikkeama（\( \sigma > 0 \)）
  \(\overline{x}\) : otoskeskiarvo
  \(n\) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \( \mu \neq \) : perusjoukon keskiarvon ehto
  \(z\) : z-arvo
  Prob : \(p\)-arvo

Tietotyyppi: Lista

• Syötettävät termit
  \( \mu \) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  \( \mu_{0} \) : oletettu perusjoukon keskiarvo
  \( \sigma \) : perusjoukon standardipoikkeama （\( \sigma > 0 \)）
  List : tietoluettelo
  Freq : frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  \( \mu \neq \) : perusjoukon keskiarvon ehto
  \(z\) : \(z\)-arvo
  Prob : \(p\)-arvo
  \( \overline{x} \) : otoskeskiarvo
  \( s_{x} \) : otoksen standardipoikkeama
  \( n \) : otoskoko

2 otoksen Z-testi
Testaa kahden keskiarvon välistä eroa, kun kahden perusjoukon standardipoikkeamat tunnetaan. 2 otoksen Z-testissä käytetään normaalijakaumaa.

\( Z=\displaystyle \frac{ \overline{x}_{1} – \overline{x}_{2} }{ \sqrt{\displaystyle \frac{{\sigma_{1}}^2}{n_{1}} +\displaystyle \frac{{\sigma_{2}}^2}{n_{2}} } } \)

\( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
\( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
\( \sigma_{1} \) : otoksen 1 perusjoukon standardipoikkeama
\( \sigma_{2} \) : otoksen 2 perusjoukon standardipoikkeama
\( n_{1} \) : otoksen 1 otoskoko
\( n_{2} \) : otoksen 2 otoskoko

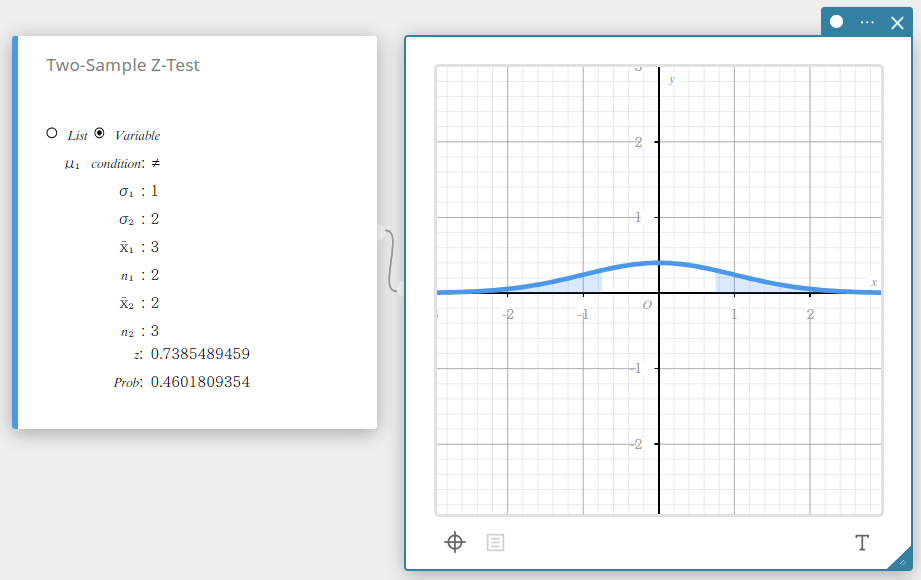
Tietotyyppi: Muuttuja

• Syötettävät termit
  \( \mu_{1} \) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  \( \sigma_{1} \) : otoksen 1 perusjoukon standardipoikkeama（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : otoksen 2 perusjoukon standardipoikkeama（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( n_{1} \) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( n_{2} \) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \(z\) : z-arvo
  Prob : \(p\)-arvo

Tietotyyppi: Lista

• Syötettävät termit
  \( \mu_{1} \) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  \( \sigma_{1} \) : otoksen 1 perusjoukon standardipoikkeama（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : otoksen 2 perusjoukon standardipoikkeama（\( \sigma_{2} > 0 \)）
  List(1) : luettelo, jossa otoksen 1 tiedot sijaitsevat
  List(2) : luettelo, jossa otoksen 2 tiedot sijaitsevat
  Freq(1) : otoksen 1 frekvenssi (1 tai luettelon nimi)
  Freq(2) : otoksen 2 frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  \(z\) : z-arvo
  Prob : \(p\)-arvo
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( s_{x_{1}} \) : otoksen 1 otoksen standardipoikkeama
  \( s_{x_{2}} \) : otoksen 2 otoksen standardipoikkeama
  \( n_{1} \) : otoksen 1 otoskoko
  \( n_{2} \) : otoksen 2 otoskoko

1 suht.os Z-testi (Yhden osuuden Z-testi)
Testaa yhden otoksen osuutta vertaamalla sitä nollahypoteesin tunnettuun osuuteen. Yhden osuuden Z-testissä käytetään normaalijakaumaa.

\(Z =\displaystyle \frac{\displaystyle \frac{x}{n} – p_{0} }{ \sqrt{\displaystyle \frac{ p_{0}(1-p_{0}) }{n} }}\)
\(p_{0}\) : odotettu otososuus
\(n\) : otoskoko

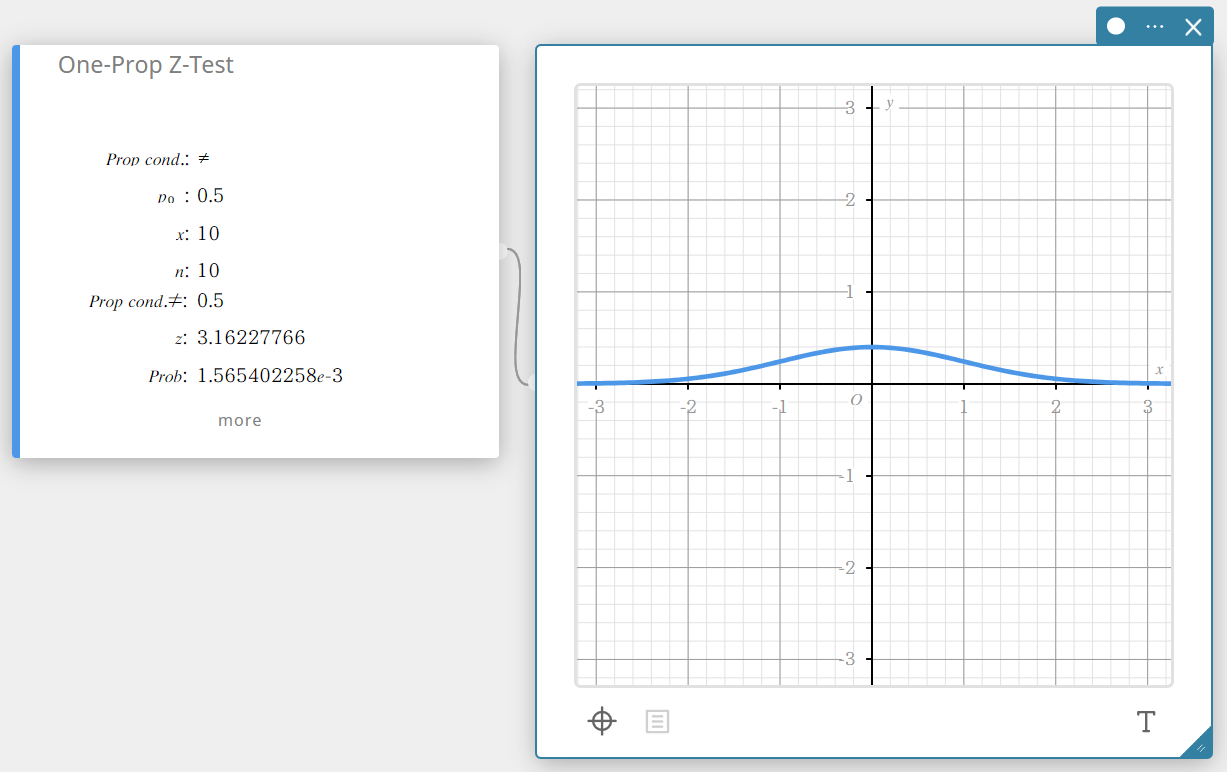
• Syötettävät termit
  Prop cond : otososuuden testausehto (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  \(p_{0}\) : odotettu otososuus（\( 0 < p_{0} < 1 \)）
  \(x\) : otosarvo (kokonaisluku, \( x \geq 0 \)）
  \(n\) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Prop Cond \(\neq\) : otososuuden testausehto
  \(z\) : z-arvo
  Prob : \(p\)-arvo
  \(\hat{p}\) : arvioitu otososuus

2 suht.os Z-testi (Kahden osuuden Z-testi)
Testaa kahden otososuuden välistä eroa. Kahden osuuden Z-testissä käytetään normaalijakaumaa.

\( Z =\displaystyle \frac{\displaystyle \frac{x_{1}}{n_{1}} -\displaystyle \frac{x_{2}}{n_{2}} }{ \sqrt{ \hat{p} \left(1-\hat{p} \right) \left(\displaystyle \frac{1}{n_{1}} +\displaystyle \frac{1}{n_{2}} \right) } }\)
\(x_{1}\) : otoksen 1 tietoarvo
\(x_{2}\) : otoksen 2 tietoarvo
\(n_{1}\) : otoksen 1 otoskoko
\(n_{2}\) : otoksen 2 otoskoko
\(\hat{p}\) : arvioitu otososuus

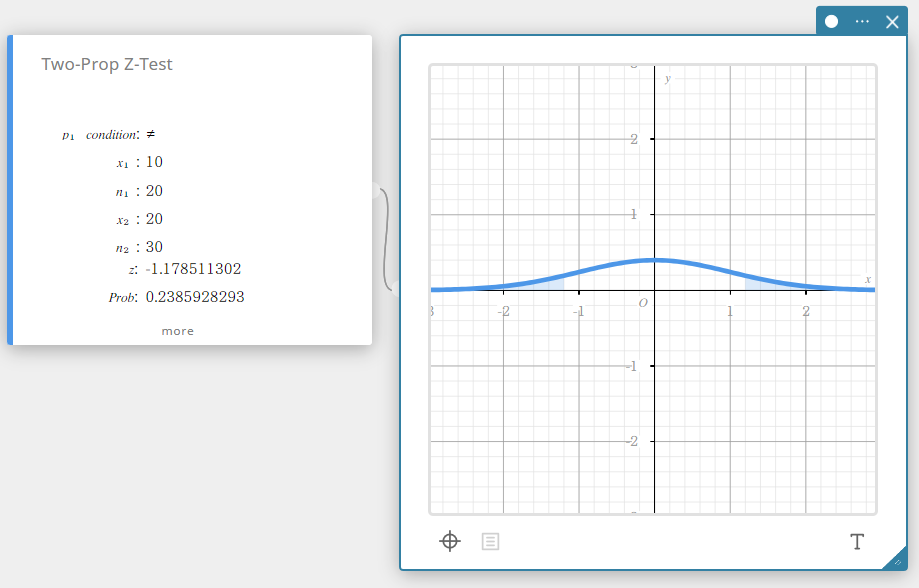
• Syötettävät termit
  \(p_{1}\) condition : otososuuden testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  \(x_{1}\) : otoksen 1 tietoarvo (kokonaisluku, \(x_{1}\) oltava pienempi tai yhtä suuri kuin \(n_{1}\))
  \(n_{1}\) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \(x_{2}\) : otoksen 2 tietoarvo (kokonaisluku, \(x_{2}\) oltava pienempi tai yhtä suuri kuin \(n_{2}\))
  \(n_{2}\) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \(z\) : z-arvo
  Prob : \(p\)-arvo
  \(\hat{p}_{1}\) : arvioitu osuus otoksesta 1
  \(\hat{p}_{2}\) : arvioitu osuus otoksesta 2
  \(\hat{p}\) : arvioitu otososuus

1 otoksen \(t\)-testi
Testaa yhden otoksen keskiarvoa vertaamalla sitä nollahypoteesin tunnettuun keskiarvoon, kun perusjoukon standardipoikkeamaa ei tunneta. 1 otoksen \(t\)-testissä käytetään \(t\) jakaumaa.

\(t =\displaystyle \frac{ \overline{x} – \mu_{0} }{\displaystyle \frac{ s_{x} }{ \sqrt{n} } }\)
\(\overline{x}\) : otoskeskiarvo
\(\mu_{0}\) : oletettu perusjoukon keskiarvo
\(s_{x}\) : otoksen standardipoikkeama
\(n\) : otoskoko

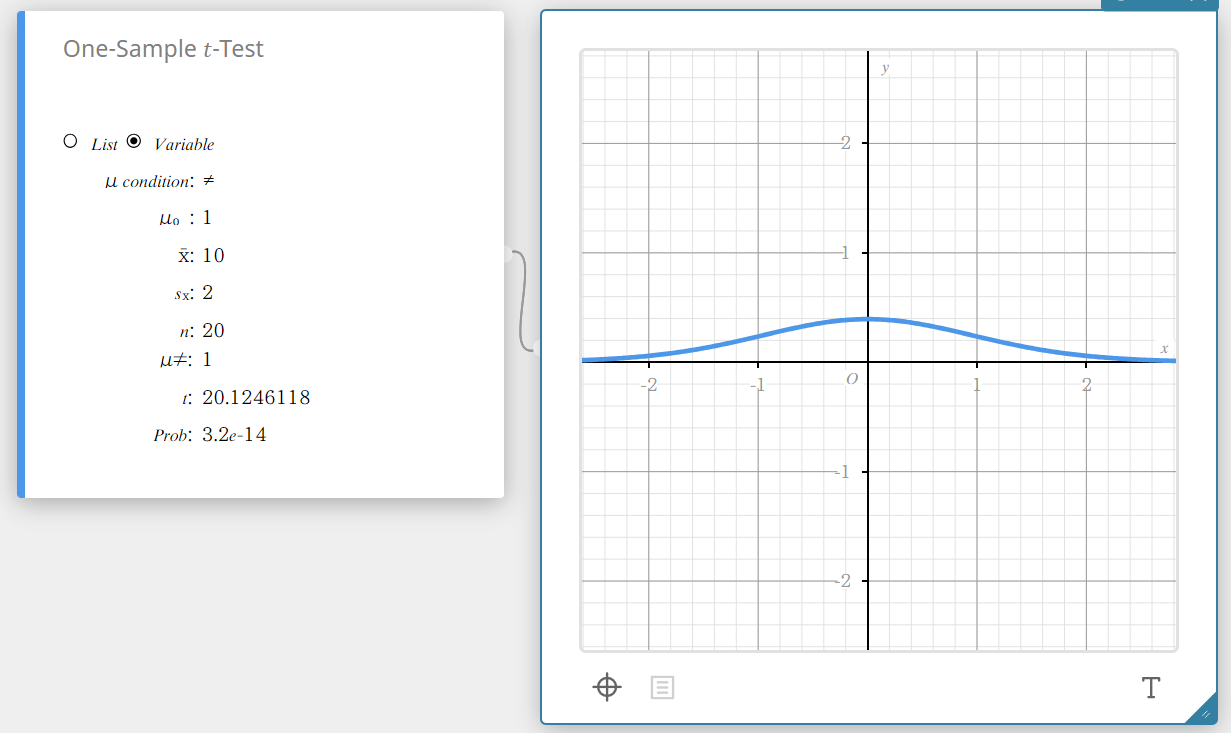
Tietotyyppi: Muuttuja

• Syötettävät termit
  \(\mu\) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  \(\mu_{0}\) : oletettu perusjoukon keskiarvo
  \(\overline{x}\) : otoskeskiarvo
  \(s_{x}\) : otoksen standardipoikkeama（\( s_{x} > 0 \)）
  \(n\) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \(\mu \ne\) : perusjoukon keskiarvon testausehdot
  \(t\) : \(t\)-arvo
  Prob : \(p\)-arvo

Tietotyyppi: Lista

• Syötettävät termit
  \(\mu\) condition : perusjoukon keskiarvon testausehdot (”\(\neq\) määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  \(\mu_{0}\) : oletettu perusjoukon keskiarvo
  List : tietoluettelo
  Freq : frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  \(\mu \ne\) : perusjoukon keskiarvon testausehdot
  \(t\) : \(t\)-arvo
  Prob : \(p\)-arvo
  \(\overline{x}\) : otoskeskiarvo
  \(s_{x}\) : otoksen standardipoikkeama
  \(n\) : otoskoko

2 otoksen \(t\)-testi
Testaa kahden keskiarvon välistä eroa, kun kahden perusjoukon standardipoikkeamia ei tunneta. 2 otoksen \(t\)-testissä käytetään \(t\) jakaumaa.

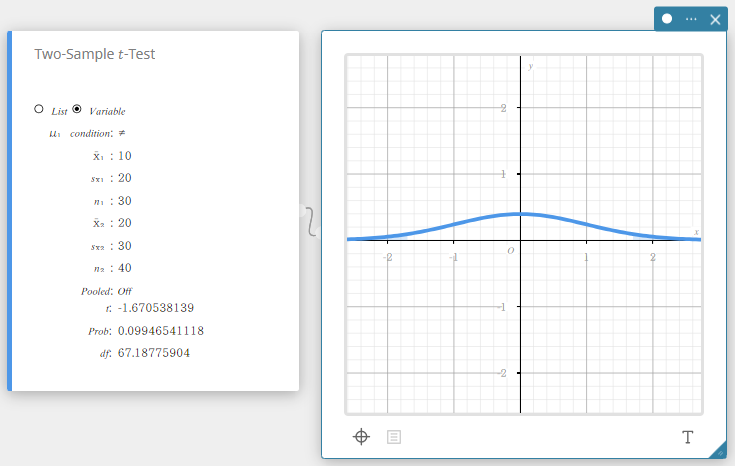
• Kun kahden perusjoukon standardipoikkeamat ovat samat (yhdistetty)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{{s_{p}}^2 \left(\displaystyle \frac{1}{n_1} + \displaystyle \frac{1}{n_2} \right)}}\)
  \(df=n_1+n_2-2\)
  \(s_p=\sqrt{ \displaystyle \frac{(n_1-1){s_{x_1}}^2 + (n_2-1){s_{x_2}}^2}{n_1+n_2-2} }\)

• Kun kahden perusjoukon standardipoikkeamat eivät ole samat (ei yhdistetty)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{\displaystyle \frac{{s_{x_1}}^2}{n_1} + \displaystyle \frac{{s_{x_2}}^2}{n_2}}}\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{(1-C)^2}{n_2-1}}\)
  \(C =\displaystyle \frac{\displaystyle \frac{{s_{x_1}}^2}{n_1}}{\displaystyle \frac{{s_{x_1}}^2}{n_1} +\displaystyle \frac{{s_{x_2}}^2}{n_2}}\)

\(x_1\): otoksen 1 tietojen otoskeskiarvo
\(x_2\): otoksen 2 tietojen otoskeskiarvo
\(s_{x_1}\) : otoksen 1 otoksen standardipoikkeama
\(s_{x_2}\) : otoksen 2 otoksen standardipoikkeama
\(s_p\) : yhdistetty otoksen standardipoikkeama
\(n_1\) : otoksen 1 otoskoko
\(n_2\) : otoksen 2 otoskoko

Tietotyyppi: Muuttuja

• Syötettävät termit
  \(\mu_1\) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  \(\overline{x}_1\) : otoksen 1 tietojen otoskeskiarvo
  \(s_{x_1}\) : otoksen 1 otoksen standardipoikkeama（\(s_{x_1} > 0\)）
  \(n_1\) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \(\overline{x}_2\) : otoksen 2 tietojen otoskeskiarvo
  \(s_{x_2}\) : otoksen 2 otoksen standardipoikkeama（\(s_{x_2} > 0\)）
  \(n_2\) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \(t\) : \(t\) -arvo
  Prob : \(p\) -arvo
  \(df\) : vapausasteet
  \(s_p\) : yhdistetty otoksen standardipoikkeama

Tietotyyppi: Lista

• Syötettävät termit
  \(\mu_1\) condition : perusjoukon keskiarvon testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  List(1) : luettelo, jossa otoksen 1 tiedot sijaitsevat
  List(2) : luettelo, jossa otoksen 2 tiedot sijaitsevat
  Freq(1) : otoksen 1 frekvenssi (1 tai luettelon nimi)
  Freq(2) : otoksen 2 frekvenssi (1 tai luettelon nimi)
  Pooled : Päällä (samat varianssit) tai Pois päällä (eri varianssit)

• Laskettavat termit
  \(t\) : \(t\)-arvo
  Prob : \(p\)-arvo
  \(df\) : vapausasteet
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( s_{x_{1}} \) : otoksen 1 otoksen standardipoikkeama
  \( s_{x_{2}} \) : otoksen 2 otoksen standardipoikkeama
  \(s_p\) : yhdistetty otoksen standardipoikkeama
  \( n_{1} \) : otoksen 1 otoskoko
  \( n_{2} \) : otoksen 2 otoskoko

Lin. reg \(t\)-testi (Lineaarisen regression \(t\)-testi)
Testaa paritettujen muuttujien välistä lineaarista suhdetta ( x , y ). Pienimmän neliösumman menetelmää käytetään määrittelemään a ja b, jotka ovat regressiokaavan kertoimia \(y = a + b \cdot x\). p -arvo on otoksen regression kaltevuuden todennäköisyys ( b ) edellyttäen, että nollahypoteesi on tosi, \(\beta = 0\). Lineaarisen regression \(t\) -testissä käytetään \(t\)-jakaumaa.

\(t=r\sqrt{\displaystyle \frac{n-2}{1-r^2}}\)
\( \displaystyle b=\left\{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) \right\} / \left\{\sum_{i=1}^n (x_i-\overline{x})^2 \right\}\)
\(a=\overline{y}-b\overline{x}\)

\(a\) : regression vakiotermi (y-leikkauspiste)
\(b\) : regressiokerroin (kaltevuus)
\(n\) : otoskoko（\(n \ge 3\)）
\(r\) : korrelaatiokerroin
\(r^2\) : determinaatiokerroin

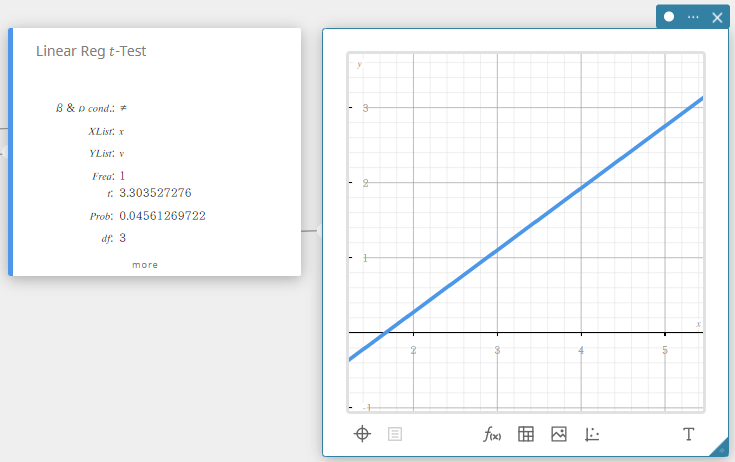
• Syötettävät termit
  \(\beta\ \&\ \rho\) cond : testausehdot (”\(\neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee alemman yksisuuntaisen testin, ”>” määrittelee ylemmän yksisuuntaisen testin.)
  XList : x -tietoluettelo
  YList : y -tietoluettelo
  Freq : frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  \(t\) : \(t\)-arvo
  Prob : \(p\)-arvoe
  \(df\) : vapausasteet
  \(a\) : regression vakiotermi (y-leikkauspiste)
  \(b\) : regressiokerroin (kaltevuus)
  se : pienimmän neliösumman regressiosuoraa koskevan arvion standardivirhe
  \(r\) : korrelaatiokerroin
  \(r^2\) : determinaatiokerroin
  SEb: pienimmän neliösumman kaltevuuden standardivirhe

\(\chi^2\)-testi
Testaa kahden matriisimuodon järjestetyn kategorisen muuttujan riippumattomuutta. Riippumattomuuden \(\chi^2\)-testi vertaa tarkasteltua matriisia odotettuun teoreettiseen matriisiin. \(\chi^2\)-testissä käytetään \(\chi^2\)-jakaumaa.

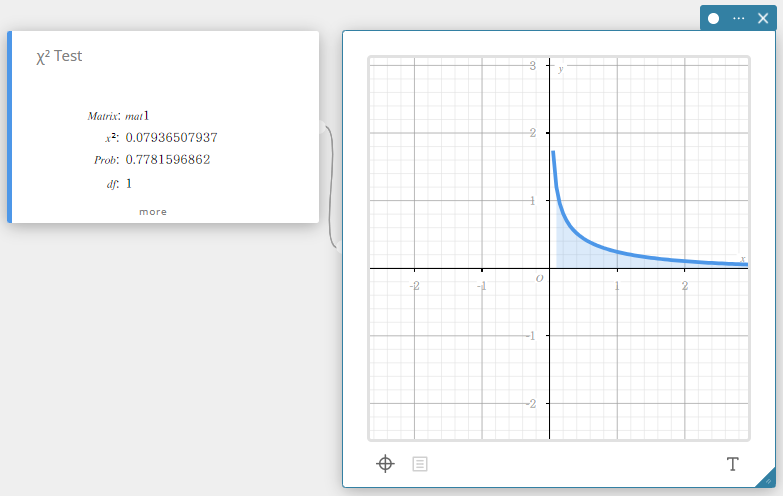
HUOMAUTUS
Matriisin vähimmäiskoko on 1×2. Jos matriisissa on vain yksi sarake, tapahtuu virhe.
Odotetun frekvenssin laskutoimituksen tulos tallennetaan järjestelmämuuttujaan nimeltä ”Odotettu”.

\( \chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{l} \displaystyle \frac{(x_{ij}-F_{ij})^2}{F_{ij}} \)
\( F_{ij}=\frac{{\displaystyle\sum_{i=1}^k}x_{ij}\times{\displaystyle\sum_{j=1}^lx_{ij}}}{{\displaystyle\sum_{i=1}^k}{\displaystyle\sum_{j=1}^l}x_{ij}} \)
\( x_{ij}\) : Tarkastellun matriisin rivin i, sarakkeen j elementti
\( F_{ij}\) : Odotetun matriisin rivin i, sarakkeen j elementti

• Syötettävät termit
  Matrix: matriisin nimi, joka sisältää havaitut arvot (positiiviset kokonaisluvut kaikissa 2×2 ja sitä suuremmissa matriiseissa; positiiviset reaaliluvut yhden rivin matriiseissa)

• Laskettavat termit
  \(\chi^2\) : \(\chi^2\)-arvo
  Prob : \(p\)-arvo
  \(df\) : vapausasteet
  Observed : tarkasteltujen arvojen syöttömatriisi
  Expected : odotettujen arvojen laskettu matriisi

\(\chi^2\) GOF-testi (\(\chi^2\) Yhteensopivuustesti)
Testaa, sopiiko otostietojen havaittu määrä tiettyyn jakaumaan. Sitä voidaan käyttää esimerkiksi määrittelemään yhdenmukaisuus normaalijakauman tai binomijakauman kanssa.

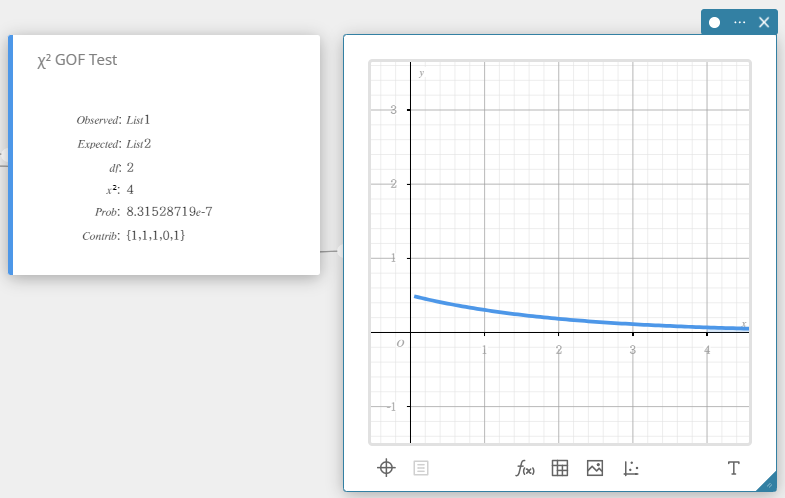
\(\chi^2=\sum_i^k \displaystyle \frac{ (O_i – E_i )^2 }{E_i}\)
\(Contrib = \left\{\displaystyle \frac{ (O_1 – E_1 )^2 }{E_1} \ \displaystyle \frac{ (O_2 – E_2 )^2 }{E_2} \cdots \displaystyle \frac{ (O_k – E_k )^2 }{E_k} \right\} \)

\(O_i\) : Tarkastellun luettelon i. elementti
\(E_i\) : Odotetun luettelon i. elementti

• Syötettävät termit
  Observed list : sen luettelon nimi, joka sisältää tarkastellut määrät (kaikki solut positiivisia kokonaislukuja)
  Expected list : sen luettelon nimi, joka on tarkoitettu odotetun frekvenssin tallentamiseen
  \(df\) : vapausasteet

• Laskettavat termit
  \(\chi^2\) : \(\chi^2\)-arvo
  Prob : \(p\)-arvo
  \(df\) : vapausasteet
  Contrib : sen luettelon nimi, joka määrittelee kunkin tarkastellun määrän vaikutuksen

2 otoksen F -testi
Testaa kahden riippumattoman otoksen otosvarianssien välistä suhdetta. 2 otoksen F -testissä käytetään F -jakaumaa.

\( F=\displaystyle \frac{{S_{x_1}}^2}{{S_{x_2}}^2}\)

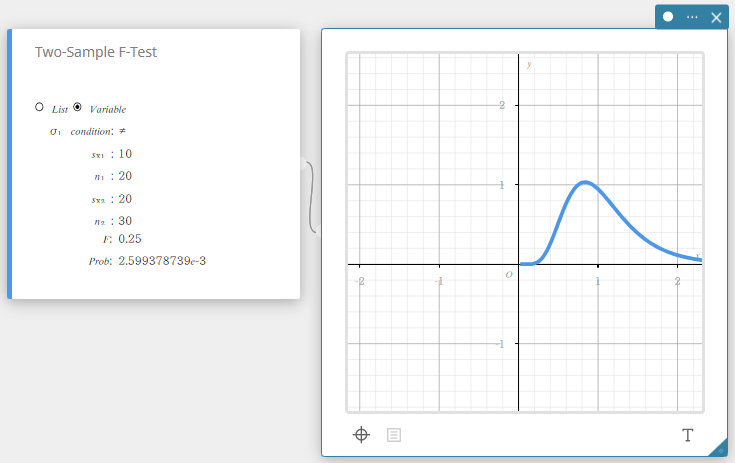
Tietotyyppi: Muuttuja

• Syötettävät termit
  \( \sigma_1\) condition: perusjoukon standardipoikkeaman testausehdot (”\( \neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  \( s_{x_1}\) : otoksen 1 otoksen standardipoikkeama（ \( s_{x_1} > 0\)）
  \( n_1\) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \( s_{x_2}\) : otoksen 2 otoksen standardipoikkeama（ \( s_{x_2} > 0\)）
  \( n_2\) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  \( F\) : F-arvo
  Prob : p-arvo

Tietotyyppi: Lista

• Syötettävät termit
  \( \sigma_1\) condition: perusjoukon standardipoikkeaman testausehdot (”\( \neq\)” määrittelee kaksisuuntaisen testin, ”<” määrittelee yksisuuntaisen testin, jossa otos 1 on pienempi kuin otos 2, ”>” määrittelee yksisuuntaisen testin, jossa otos 1 on suurempi kuin otos 2.)
  List(1) : luettelo, jossa otoksen 1 tiedot sijaitsevat
  List(2) : luettelo, jossa otoksen 2 tiedot sijaitsevat
  Freq(1) : otoksen 1 frekvenssi (1 tai luettelon nimi)
  Freq(2) : otoksen 2 frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  \( F\) : F-arvo
  Prob : p-arvo
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( s_{x_{1}} \) : otoksen 1 otoksen standardipoikkeama
  \( s_{x_{2}} \) : otoksen 2 otoksen standardipoikkeama
  \( n_{1} \) : otoksen 1 otoskoko
  \( n_{2} \) : otoksen 2 otoskoko

1-suunt ANOVA (Yksisuuntainen varianssianalyysi)
Testaa hypoteesia, jossa useampien perusjoukkojen keskiarvot ovat samat. Se vertaa yhden tai useamman ryhmän keskiarvoa yhden muuttujan tai tekijän perusteella.

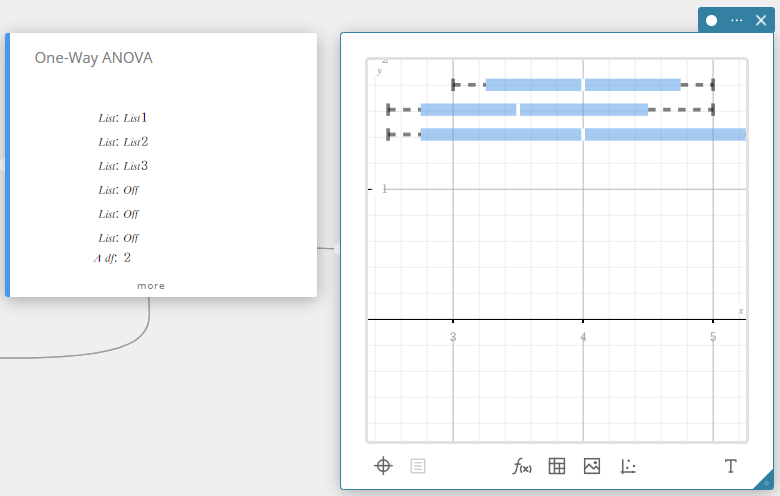
• Syötettävät termit
  FactorList(A) : luettelo, jossa sijaitsevat tekijän A tasot
  DependentList : luettelo, jossa sijaitsevat otoksen tiedot

• Laskettavat termit
  A df : tekijän A vapausasteet
  A MS : tekijän A keskineliö
  A SS : tekijän A neliöiden summa
  A F : F Tekijän A F -arvo
  A p : p Tekijän A p -arvo
  Err df : virheen vapausasteet
  Err MS : virheen keskineliö
  Err SS : virheen neliöiden summa

2-suunt ANOVA (Kaksisuuntainen varianssianalyysi)
Testaa hypoteesia, jossa useampien perusjoukkojen keskiarvot ovat samat. Se tutkii jokaisen muuttujan vaikutusta riippumattomasti ja niiden vaikutusta toisiinsa riippuvan muuttujan perusteella.

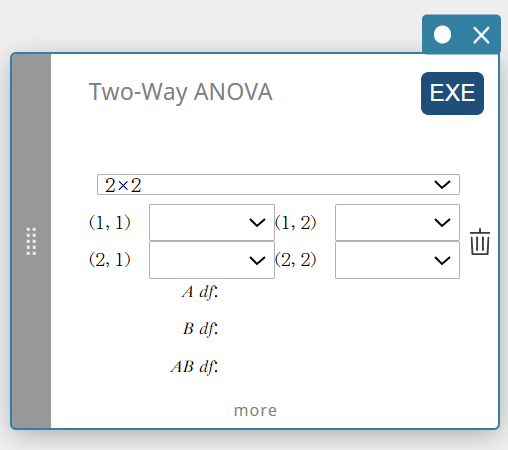
• Syötettävät termit
  2×2: tietotaulukon tyyppi
  FactorList(A) : luettelo, jossa sijaitsevat tekijän A tasot
  FactorList(B) : luettelo, jossa sijaitsevat tekijän B tasot
  DependentList: luettelo, jossa sijaitsevat otoksen tiedot

• Laskettavat termit
  A df : tekijän A vapausasteet
  A MS : tekijän A keskineliö
  A SS : tekijän A neliöiden summa
  A F : F Tekijän A F -arvo
  A p : p Tekijän A p -arvo
  B df : tekijän B vapausasteet
  B MS : tekijän B keskineliö
  B SS : tekijän B neliöiden summa
  B F : Tekijän B F-arvo
  B p : Tekijän B p-arvo
  AB df : tekijän A × tekijän B vapausasteet
  AB MS : tekijän A × tekijän B keskineliö
  AB SS : tekijän A × tekijän B neliöiden summa
  AB F : Tekijän A × tekijän B F-arvo
  AB p : Tekijän A × tekijän B p-arvo
  Err df : virheen vapausasteet
  Err MS : virheen keskineliö
  Err SS : virheen neliöiden summa

Luottamusvälit

1 otoksen Z-väli
Laskee perusjoukon keskiarvon luottamusvälin otoksen keskiarvon ja tunnetun perusjoukon standardipoikkeaman perusteella.

\(Lower = \overline{x}-Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(Upper = \overline{x}+Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(\alpha\) on merkitsevyystaso ja \(100(1 – \alpha)\%\) on luottamustaso. Kun luottamustaso on esimerkiksis \(95\%\), syötetään 0,95, joka tuottaa α = 1 – 0,95 = 0,05.

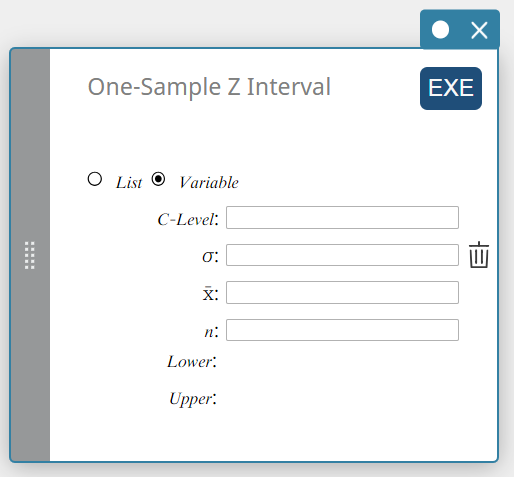
Tietotyyppi: Muuttuja

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : perusjoukon standardipoikkeama（\( \sigma > 0 \)）
  \( \overline{x} \) : otoskeskiarvo
  \( n \) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)

Tietotyyppi: Lista

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : perusjoukon standardipoikkeama（\( \sigma > 0 \)）
  List: luettelo, jossa otoksen tiedot sijaitsevat
  Freq : otoksen frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \( \overline{x} \) : otoskeskiarvo
  \( s_{x} \) : otoksen standardipoikkeama
  \( n \) : otoskoko

2 otoksen Z-väli
Laskee luottamusvälin perusjoukkojen keskiarvojen erolle otoskeskiarvojen eron perusteella, kun perusjoukkojen standardipoikkeamat tunnetaan.


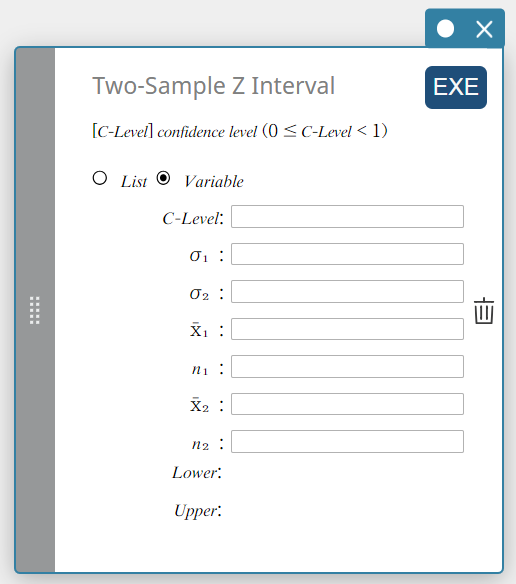
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)

Tietotyyppi: Muuttuja

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : otoksen 1 perusjoukon standardipoikkeama（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : otoksen 2 perusjoukon standardipoikkeama（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( n_{1} \) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( n_{2} \) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)

Tietotyyppi: Lista

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : otoksen 1 perusjoukon standardipoikkeama（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : otoksen 2 perusjoukon standardipoikkeama（\( \sigma_{2} > 0 \)）
  List(1) : luettelo, jossa otoksen 1 tiedot sijaitsevat
  List(2) : luettelo, jossa otoksen 2 tiedot sijaitsevat
  Freq(1) : otoksen 1 frekvenssi (1 tai luettelon nimi)
  Freq(2) : otoksen 2 frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( s_{x_{1}} \) : otoksen 1 otoksen standardipoikkeama
  \( s_{x_{2}} \) : otoksen 2 otoksen standardipoikkeama
  \( n_{1} \) : otoksen 1 otoskoko
  \( n_{2} \) : otoksen 2 otoskoko

1 suht.os Z-väli (Yhden osuuden Z-väli)
Laskee luottamusvälin perusjoukon osuudelle yhden otososuuden perusteella.


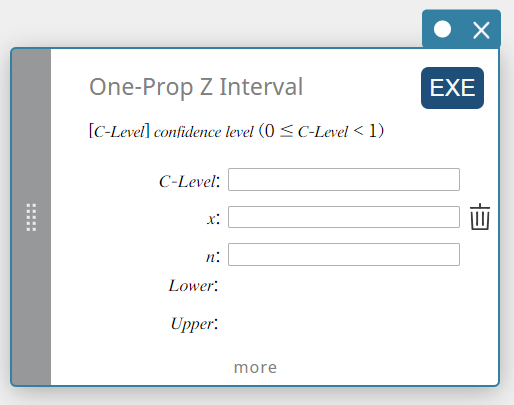
\(Lower =\displaystyle \frac{x}{n}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
\(Upper =\displaystyle \frac{x}{n}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( x \) : tiedot (0 tai positiivinen kokonaisluku)
  \( n \) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \(\hat{p}\) : arvioitu otososuus

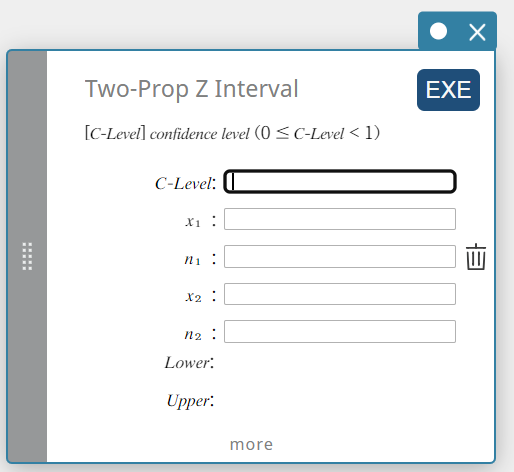
2 suht.os Z-väli (Kahden osuuden Z-väli)
Laskee luottamusvälin perusjoukkojen osuuksien erolle kahden osuuden z-välin eron perusteella.


\( Lower =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1- \displaystyle\frac{x_1}{n_1} \right) }{n_1} + \displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1- \displaystyle \frac{x_2}{n_2} \right) }{n_2} } \)
\( Upper =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1-\displaystyle \frac{x_1}{n_1} \right) }{n_1} +\displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1-\displaystyle\frac{x_2}{n_2} \right) }{n_2} } \)

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \(x_{1}\) : otoksen 1 tietoarvo (kokonaisluku, \(x_{1}\) oltava pienempi tai yhtä suuri kuin \(n_{1}\))
  \(n_{1}\) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \(x_{2}\) : otoksen 2 tietoarvo (kokonaisluku, \(x_{2}\) oltava pienempi tai yhtä suuri kuin \(n_{2}\))
  \(n_{2}\) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \(\hat{p}_{1}\) : arvioitu osuus otoksesta 1
  \(\hat{p}_{2}\) : arvioitu osuus otoksesta 2

1 otoksen \(t\)-väli
Laskee perusjoukon keskiarvon luottamusvälin otoksen keskiarvon ja otoksen standardipoikkeaman perusteella, kun perusjoukon standardipoikkeamaa ei tunneta.

\(Lower = \overline{x}-t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
\(Upper = \overline{x}+t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)

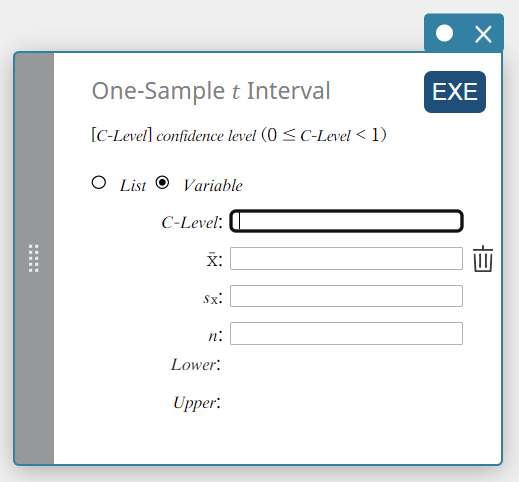
Tietotyyppi: Muuttuja

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x} \) : otoskeskiarvo
  \(s_{x}\) : otoksen standardipoikkeama（\( s_{x} \ge 0 \)）
  \(n\) : otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)

Tietotyyppi: Lista

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  List: luettelo, jossa otoksen tiedot sijaitsevat
  Freq : otoksen frekvenssi (1 tai luettelon nimi)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \( \overline{x} \) : otoskeskiarvo
  \( s_{x} \) : otoksen standardipoikkeama
  \( n \) : otoskoko

2 otoksen \(t\)-väli
Laskee luottamusvälin perusjoukkojen keskiarvojen erolle otoskeskiarvojen eron ja otoksen standardipoikkeamien perusteella, kun perusjoukkojen standardipoikkeamia ei tunneta.

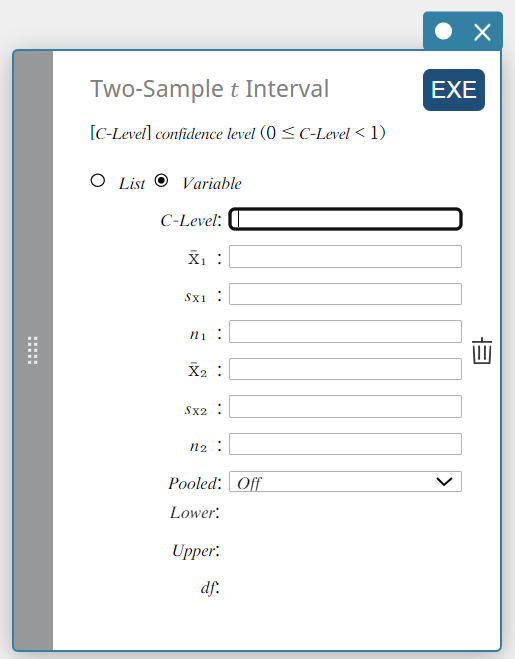
• Kun kahden perusjoukon standardipoikkeamat ovat samat (yhdistetty)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  

• Kun kahden perusjoukon standardipoikkeamat eivät ole samat (ei yhdistetty)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{ \left( 1-C \right) ^2}{n_2-1}}\)
  \(C=\displaystyle \frac{\displaystyle \frac{{S_{x_1}}^2}{n_1}}{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1} + \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  

Tietotyyppi: Muuttuja

• Syötettävät termit
  C-Level : luottamustaso（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \(s_{x_1}\) : otoksen 1 otoksen standardipoikkeama（\(s_{x_1} \ge 0\)）
  \( n_{1} \) : otoksen 1 otoskoko (positiivinen kokonaisluku)
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \(s_{x_2}\) : otoksen 2 otoksen standardipoikkeama（\(s_{x_2} \ge 0\)）
  \( n_{2} \) : otoksen 2 otoskoko (positiivinen kokonaisluku)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \(df\) : vapausasteet
  \(s_p\) : yhdistetty otoksen standardipoikkeama

Tietotyyppi: Lista

• Syötettävät termit
  C-Level : luottamustaso (\(0 \le\) C-Level \(\lt 1\)）
  List(1) : luettelo, jossa otoksen 1 tiedot sijaitsevat
  List(2) : luettelo, jossa otoksen 2 tiedot sijaitsevat
  Freq(1) : otoksen 1 frekvenssi (1 tai luettelon nimi)
  Freq(2) : otoksen 2 frekvenssi (1 tai luettelon nimi)
  Pooled : Päällä (samat varianssit) tai Pois päällä (eri varianssit)

• Laskettavat termit
  Lower : välin alaraja (vasen reuna)
  Upper : välin yläraja (oikea reuna)
  \(df\) : vapausasteet
  \( \overline{x}_{1} \) : otoksen 1 tietojen otoskeskiarvo
  \( \overline{x}_{2} \) : otoksen 2 tietojen otoskeskiarvo
  \( s_{x_{1}} \) : otoksen 1 otoksen standardipoikkeama
  \( s_{x_{2}} \) : otoksen 2 otoksen standardipoikkeama
  \(s_p\) : yhdistetty otoksen standardipoikkeama
  \( n_{1} \) : otoksen 1 otoskoko
  \( n_{2} \) : otoksen 2 otoskoko

Jakauma

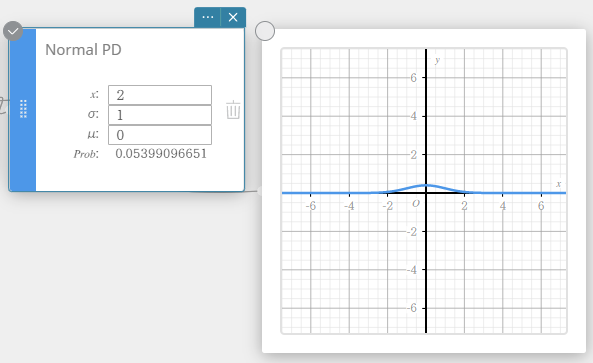
Normaali PD (Normaali todennäköisyystiheys)
Laskee tietyn arvon normaalin todennäköisyystiheyden.
Määritelmät σ = 1 ja μ= 0 tuottavat standardin normaalijakauman.

\(\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \qquad (\sigma>0)\)

• Syötettävät termit
  \( x \) : tietoarvo
  \( \sigma \) : perusjoukon standardipoikkeama (\( \sigma > 0 \))
  \( \mu \) : perusjoukon keskiarvo

• Laskettavat termit
  Prob : normaali todennäköisyystiheys

Normaali CD (Normaali kumulatiivinen jakauma)
Laskee normaalijakauman kumulatiivisen todennäköisyyden alarajan ( a ) ja ylärajan välillä ( b ).

\(\displaystyle p=\frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{ \scriptscriptstyle -\frac{(x-\mu)^2}{2\sigma^2} }dx\)

• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \( \sigma \) : perusjoukon standardipoikkeama (\( \sigma > 0 \))
  \(\mu\) : perusjoukon keskiarvo

• Laskettavat termit
  Prob : normaalijakauman todennäköisyys p
  z Low : standardoidun alarajan z-arvo
  z Up : standardoidun ylärajan z-arvo

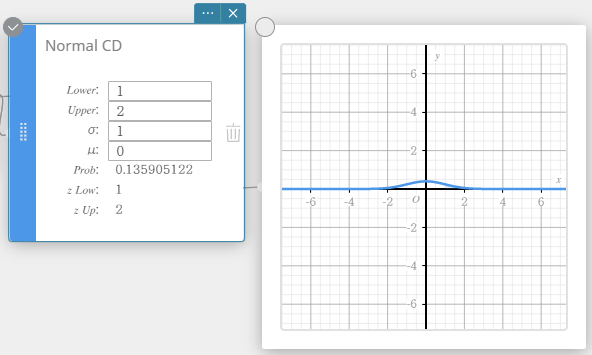
Studentin \(t\) PD (Studentin \(t\)-todennäköisyystiheys)
Laskee Studentin t-todennäköisyystiheyden tietylle arvolle.


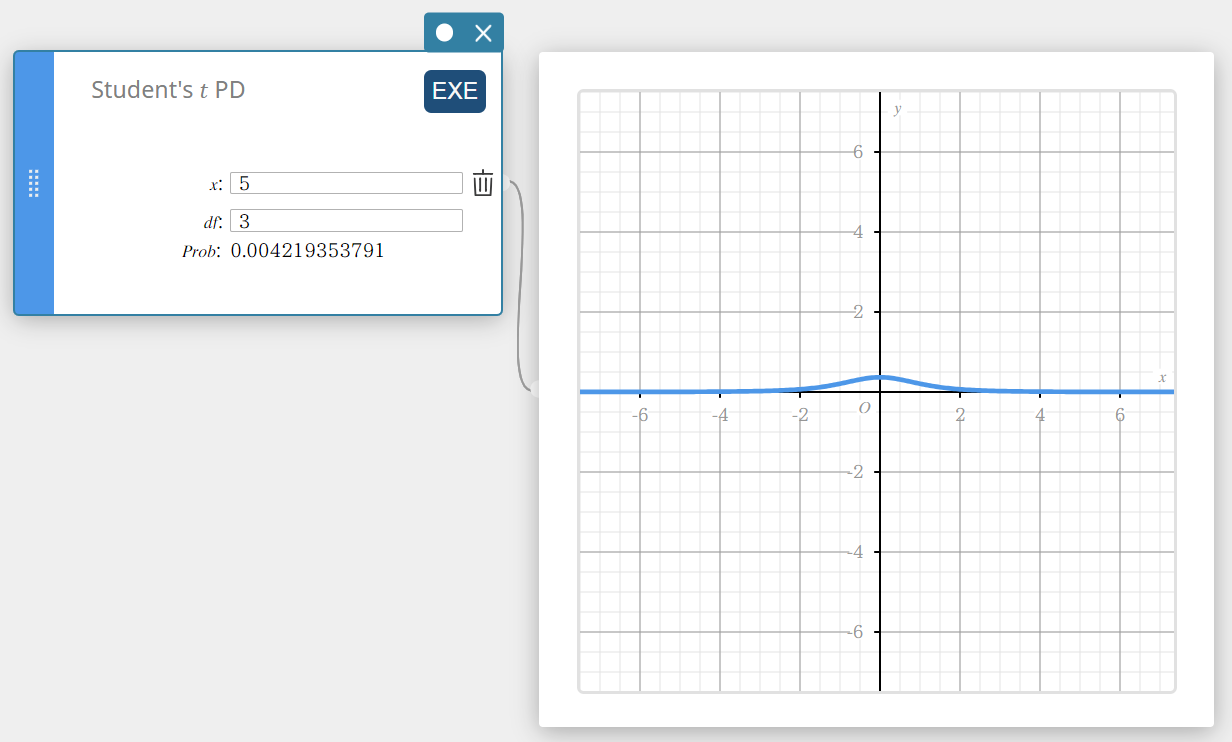
\(f(x)=\frac{\Gamma\left({\displaystyle\frac{df+1}2}\right)}{\Gamma\left({\displaystyle\frac{df}2}\right)}\times\frac{\left(1+{\displaystyle\frac{x^2}{df}}\right)^{-{\displaystyle\frac{df+1}2}}}{\sqrt{\pi\cdot df}}\)

• Syötettävät termit
  \( x \) : tietoarvo
  \(df\) : vapausasteet（\(df \gt 0\)）

• Laskettavat termit
  Prob : Studentin t-todennäköisyystiheys

Studentin \(t\) CD (Studentin \(t\) -kumulatiivinen jakauma)
Laskee Studentin t-jakauman kumulatiivisen todennäköisyyden alarajan ( a ) ja ylärajan ( b ) välillä.


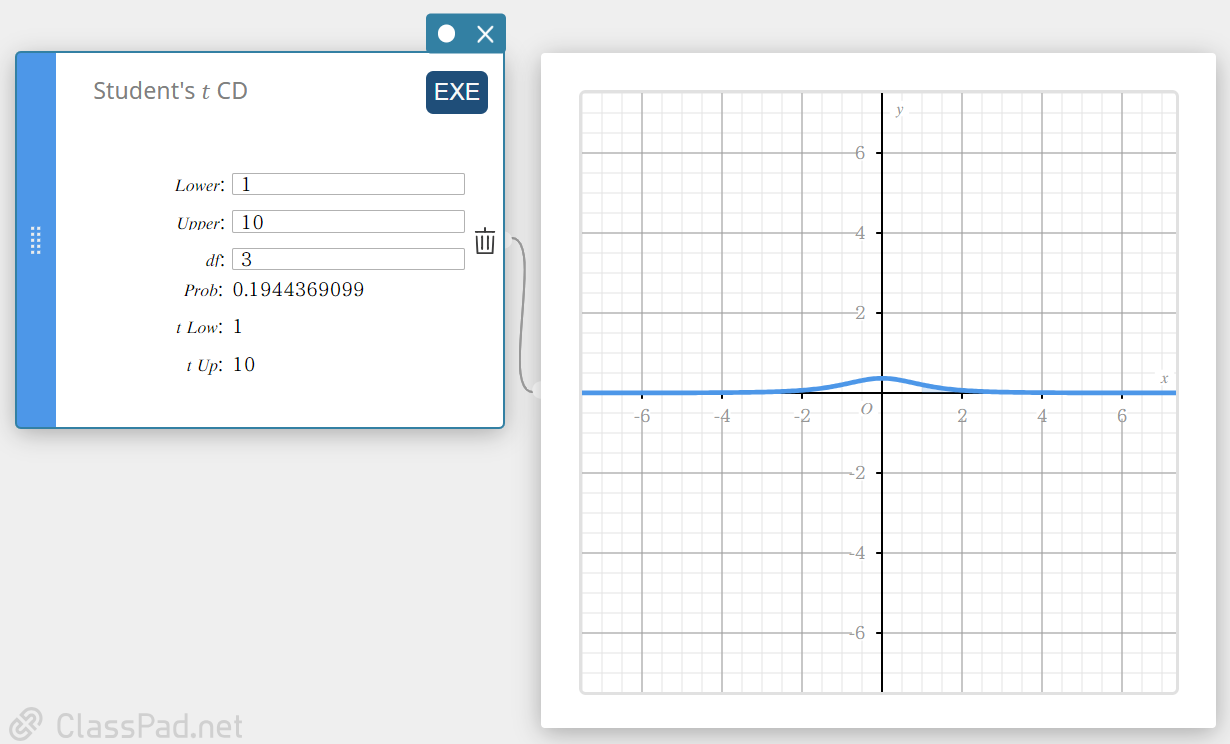
\( p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{df+1}{2} \right) }{\Gamma \left(\displaystyle \frac{df}{2} \right) \sqrt{\pi \cdot df}}\int_a^b \left(\displaystyle 1+\frac{x^2}{df} \right) ^{-\displaystyle\frac{df+1}{2}}dx \)

• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \(df\) : vapausasteet（\(df \gt 0\)）

• Laskettavat termit
  Prob : Studentin t-jakauma
  t Low : syötetyn alarajan arvo
  t Up : syötetyn ylärajan arvo

\(\chi^2\) PD (\(\chi^2\)-todennäköisyystiheys)
Laskee tietyn arvon \(\chi^2\):n todennäköisyystiheyden.


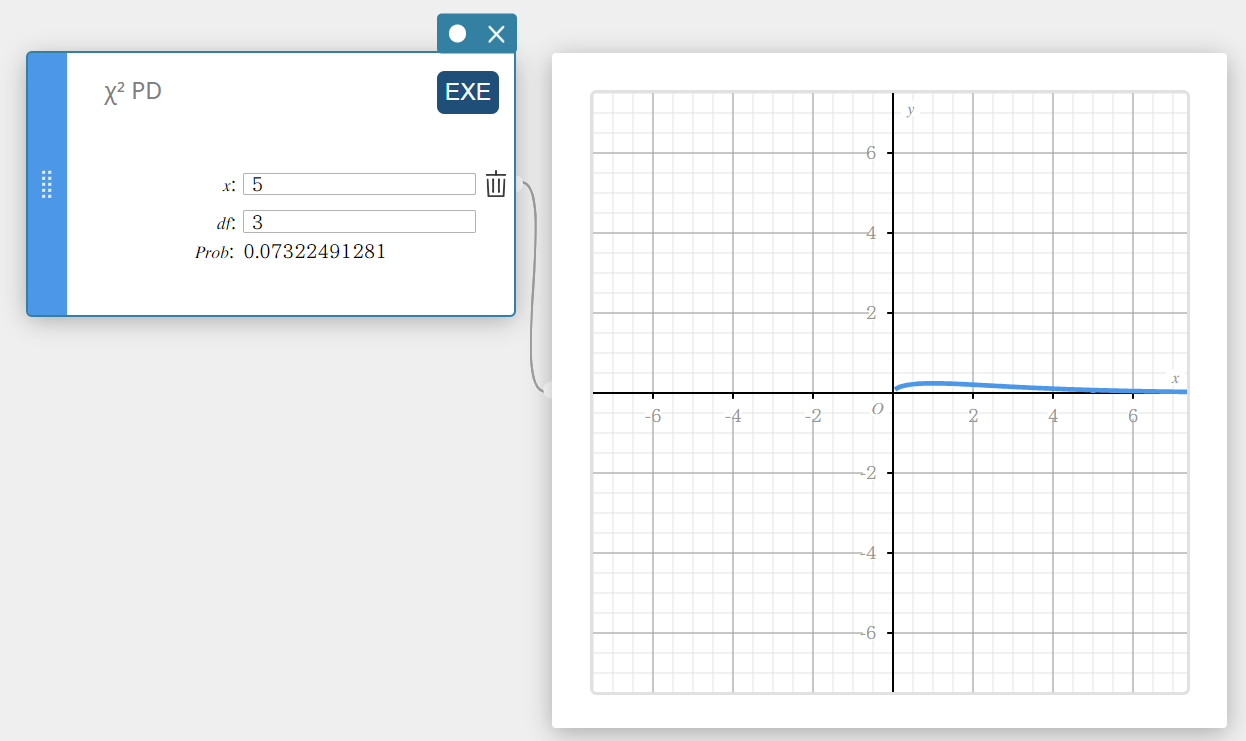
\(f \left( x \right) =\displaystyle\frac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}\)

• Syötettävät termit
  \( x \) : tietoarvo
  \(df\) : vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  Prob : \(\chi^2\):n todennäköisyystiheys

\(\chi^2\) CD (\(\chi^2\)-kumulatiivinen jakauma)
Laskee \(\chi^2\)-jakauman kumulatiivisen todennäköisyyden alarajan ja ylärajan välillä.


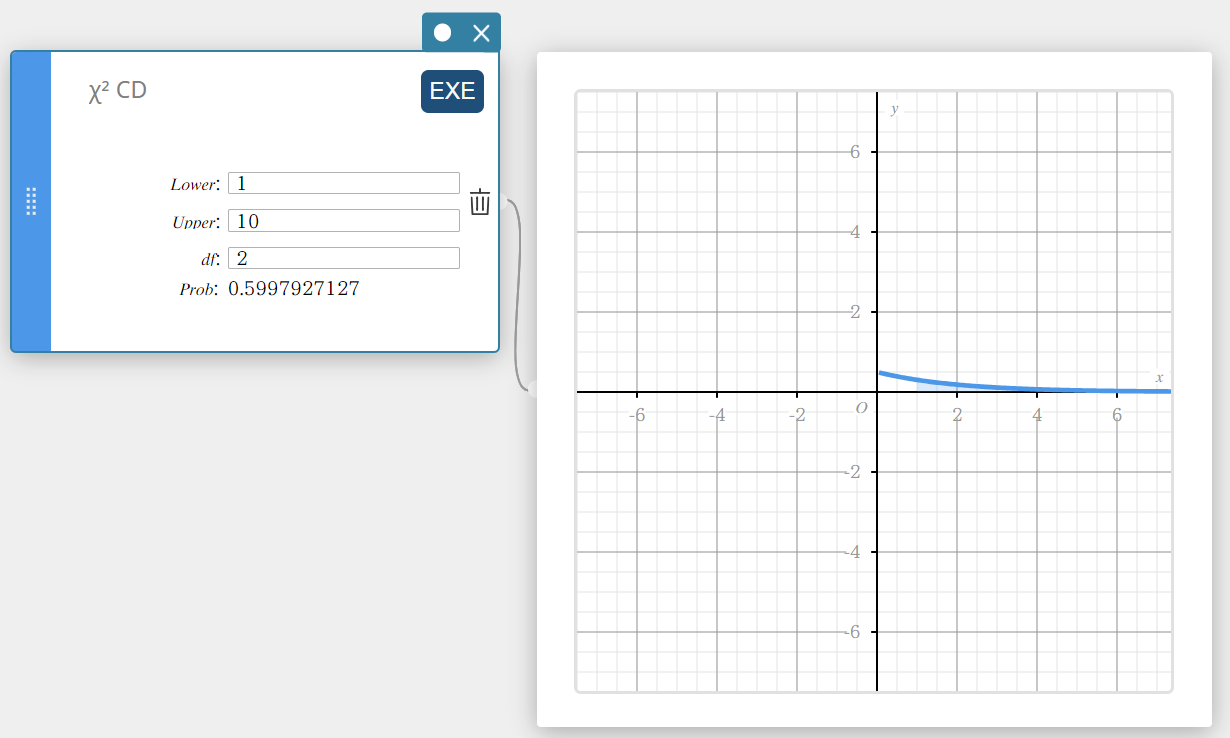
\(p=\cfrac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}\int_a^b x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}dx\)

• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \(df\) : vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  Prob : \(\chi^2\)-jakauman todennäköisyys

F PD (F-todennäköisyystiheys)
Laskee tietyn arvon F-todennäköisyystiheyden.


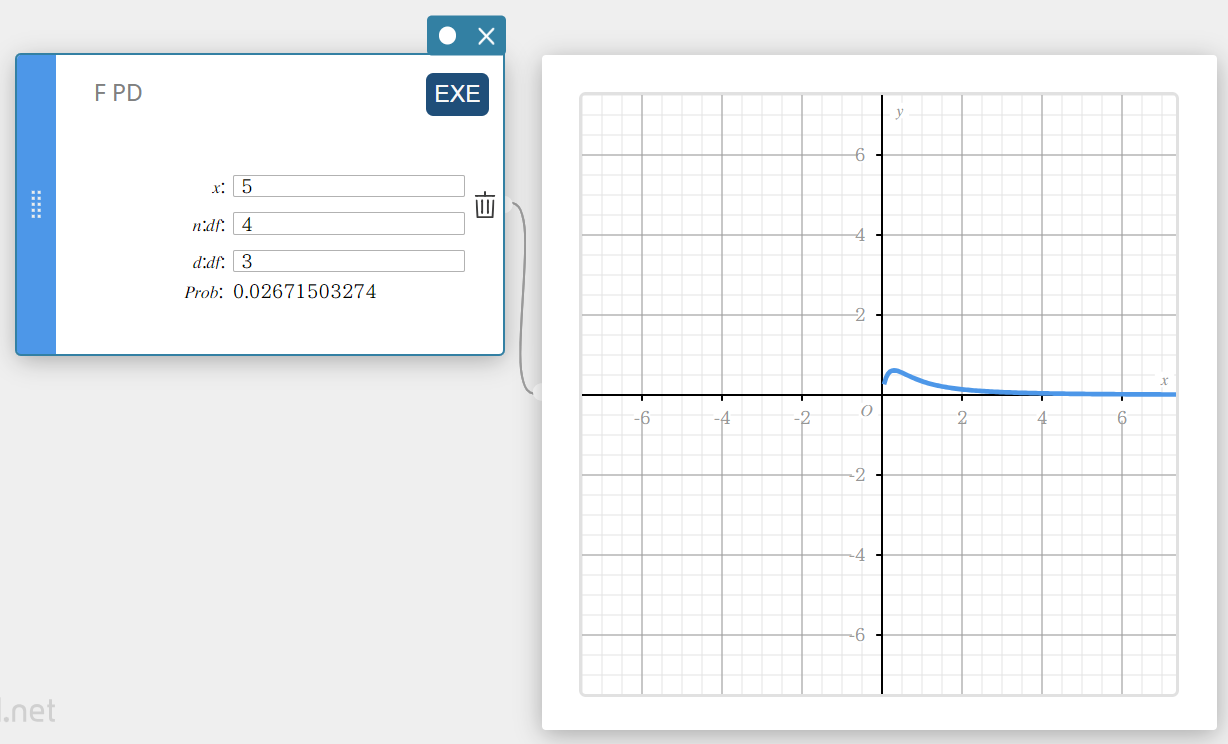
\(f(x)=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}\)

• Syötettävät termit
  \( x \) : tietoarvo
  \( n:df \) : osoittajan vapausasteet (positiivinen kokonaisluku)
  \( d:df \) : nimittäjän vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  Prob : F-todennäköisyystiheys

F CD (F-kumulatiivinen jakauma)
PalauttaaF-jakauman kumulatiivisen todennäköisyyden alarajan ja ylärajan välillä.


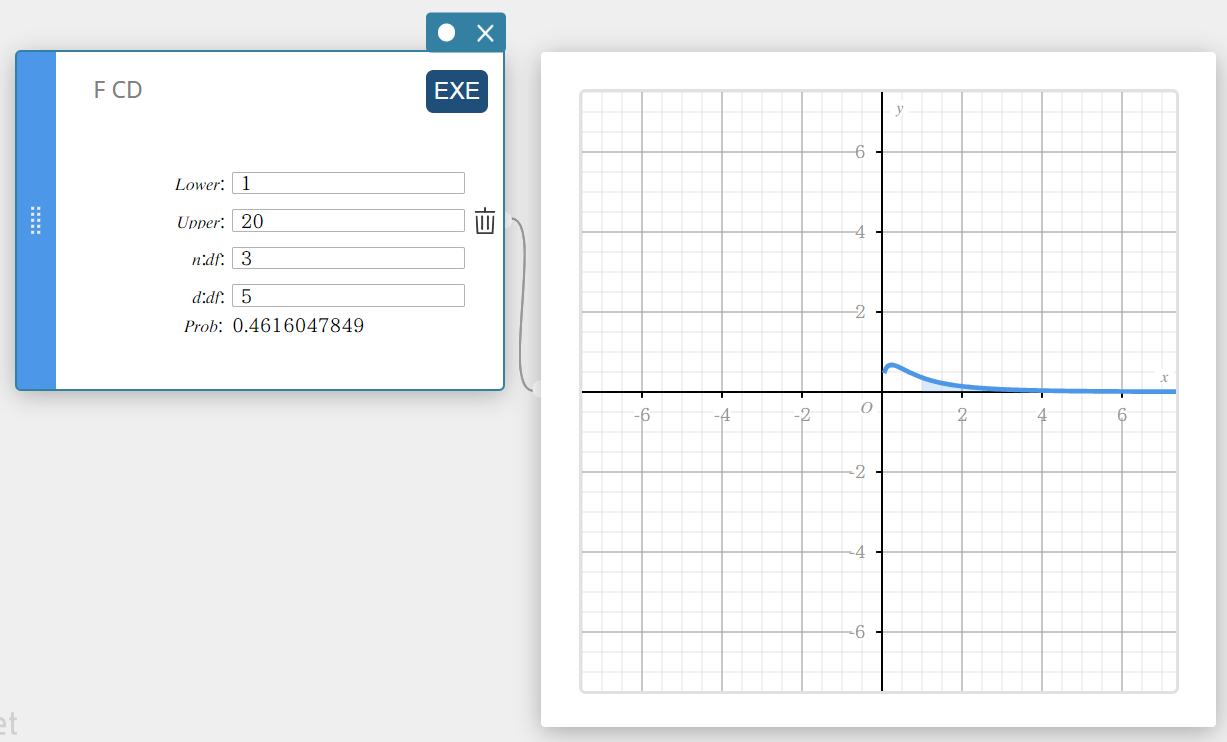
\(p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}\int_a^b x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}dx\)

• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \( n:df \) : osoittajan vapausasteet (positiivinen kokonaisluku)
  \( d:df \) : nimittäjän vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  Prob : F-jakauman todennäköisyys

Binomi-PD (Binomijakauman todennäköisyys)
Laskee binomijakauman todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.


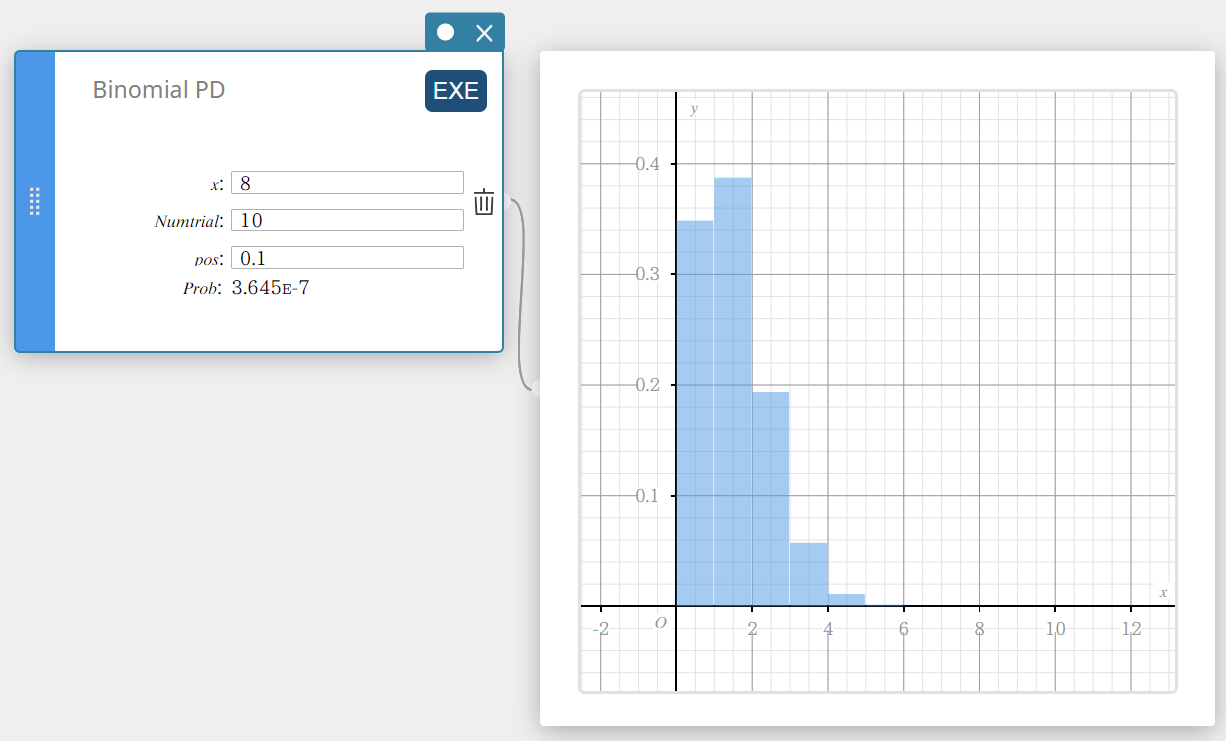
\(f(x)={}_nC_xp^x(1-p)^{n-x} \quad (x=0,1, \cdots,n)\)

\(p\) : onnistumisen todennäköisyys（(0 \(≤\) p \(≤\) 1)
\(n\) : kokeiden määrä

• Syötettävät termit
  \( x \) : tietty koe (kokonaisluku välillä 0 ja n )
  Numtrial : kokeiden lukumäärä n (kokonaisluku, n ≥ 0)
  pos : onnistumisen todennäköisyys p (0 \(≤\) p \(≤\) 1)

• Laskettavat termit
  Prob : binomijakauman todennäköisyys

Binomi-CD (Kumulatiivinen binomijakauma)
Laskee binomijakauman kumulatiivisen todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

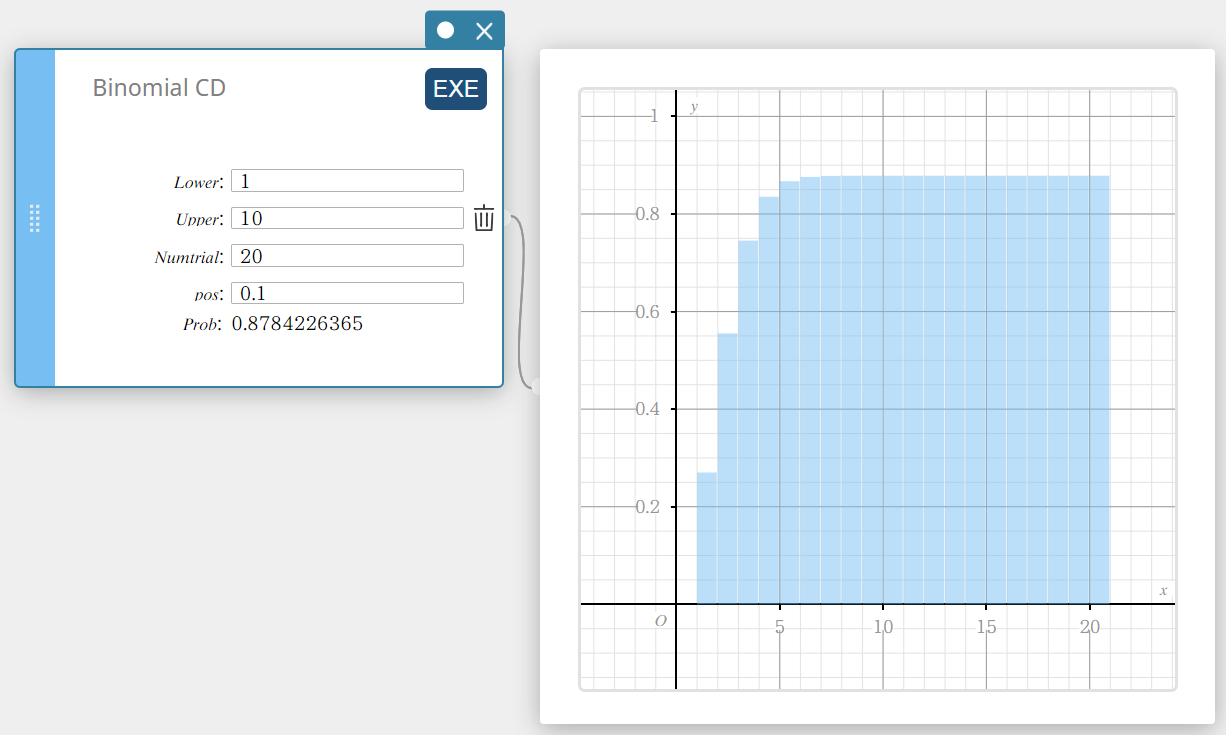
• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  Numtrial : kokeiden lukumäärä n (kokonaisluku, n \(≥\) 1)
  pos : onnistumisen todennäköisyyss p (0 \(≤\) p \(≤\) 1)

• Laskettavat termit
  Prob : binomijakauman kumulatiivinen todennäköisyys

Poisson PD (Poissonin jakauman todennäköisyys)
Laskee Poissonin jakauman todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

\(f(x)=\displaystyle\frac{e^{-\lambda} \lambda^x}{x!} \qquad (x=0,1,2,\cdots)\)

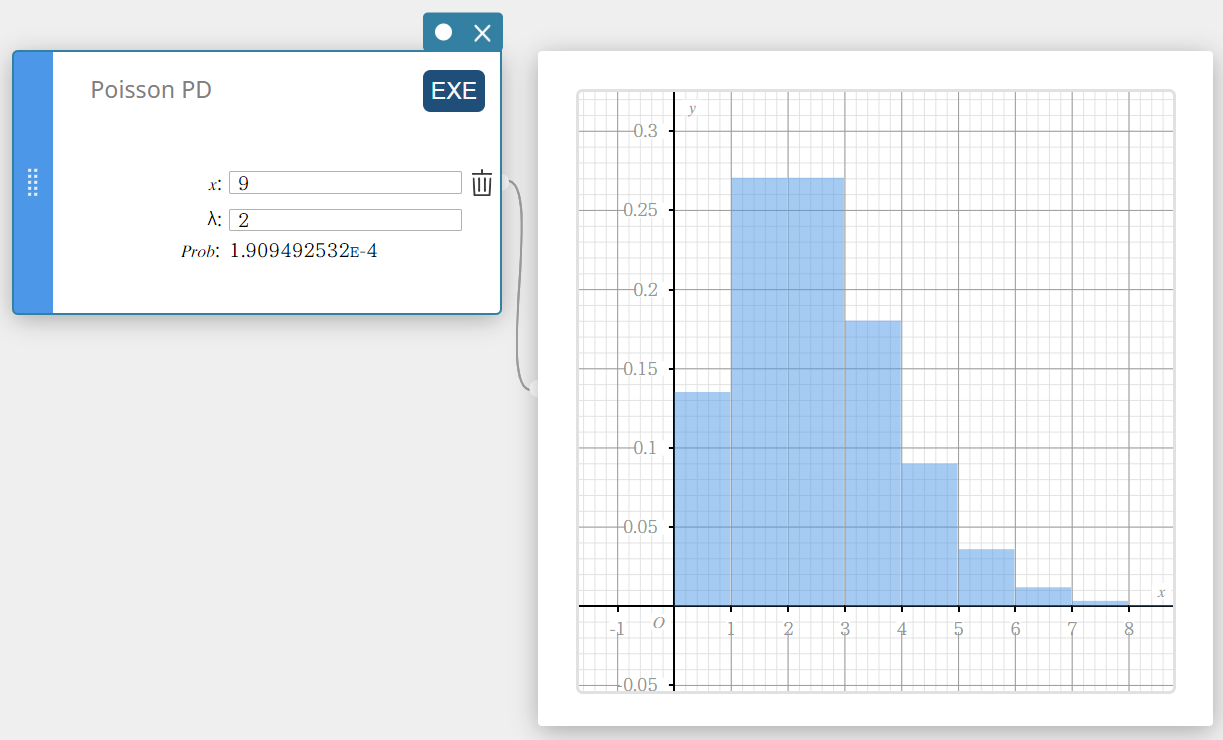
• Syötettävät termit
  \( x \) : tietty koe (kokonaisluku, x \(≥\) 0)
  \( \lambda \) : keskiarvo（\(\lambda \gt 0\)）
• Laskettavat termit
  Prob : Poissonin todennäköisyys

Poisson CD (Poissonin kumulatiivinen jakauma)
Laskee Poissonin jakauman kumulatiivisen todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

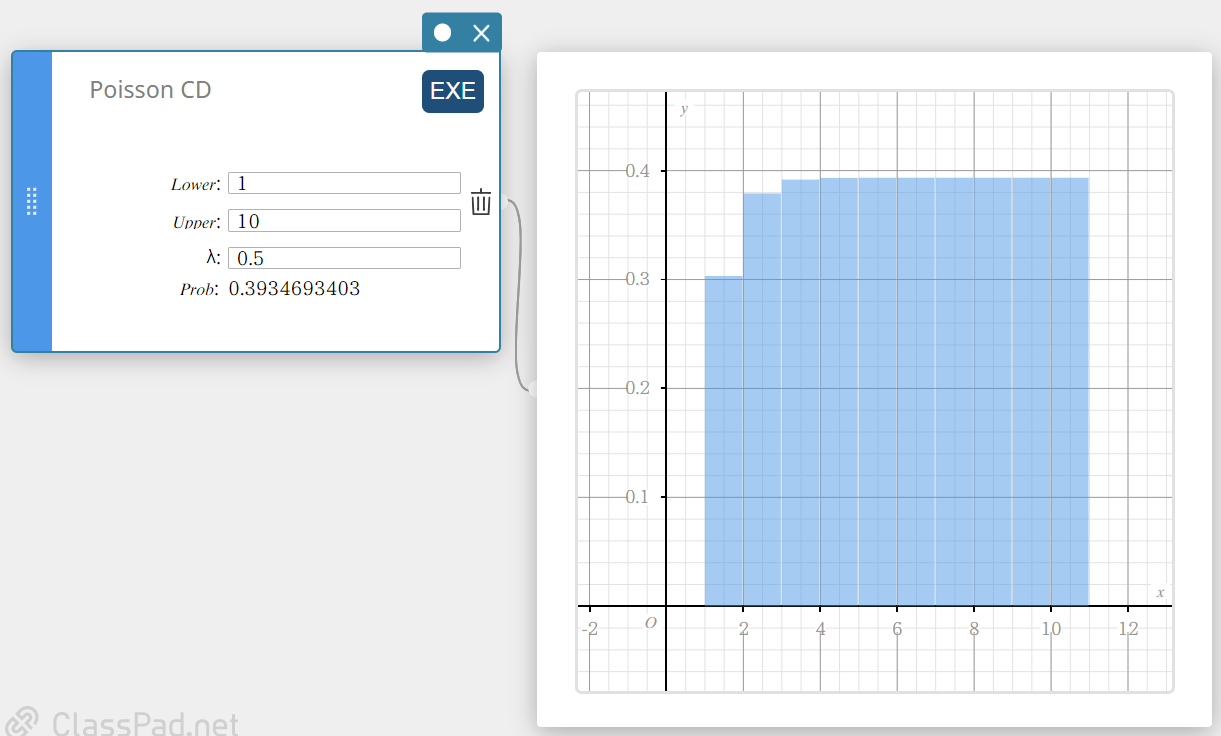
• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \( \lambda \) : keskiarvo（\(\lambda \gt 0\)）

• Laskettavat termit
  Prob : Poissonin kumulatiivinen todennäköisyys

Geometr. PD (Geometrisen jakauman todennäköisyys)
Laskee geometrisen jakauman todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

\( f(x)=p(1-p)^{x-1} \qquad (x=1,2,3,\cdots) \)

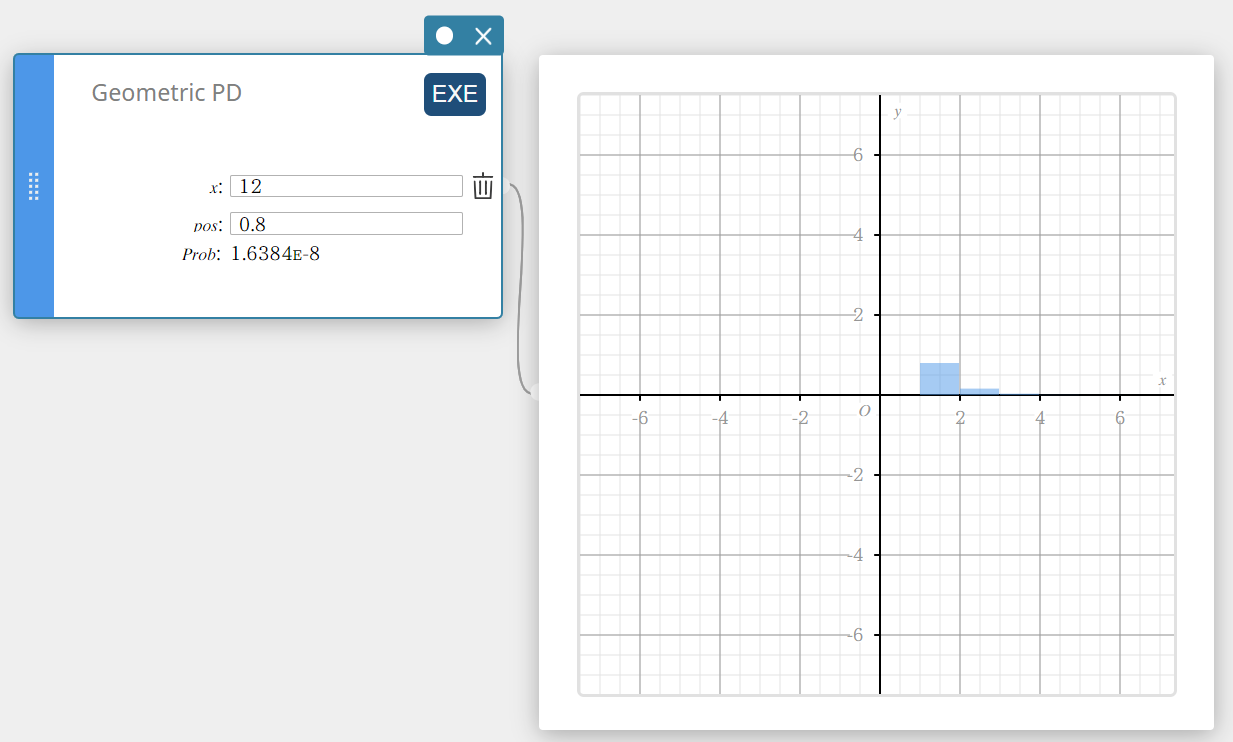
• Syötettävät termit
  \( x \) : tietty koe (positiivinen kokonaisluku)
  pos : onnistumisen todennäköisyys p (0 \(≤\) p \(≤\) 1)

• Laskettavat termit
  Prob : geometrinen todennäköisyys

Geometr. CD (Kumulatiivinen geometrinen jakauma)
Laskee geometrisen jakauman kumulatiivisen todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

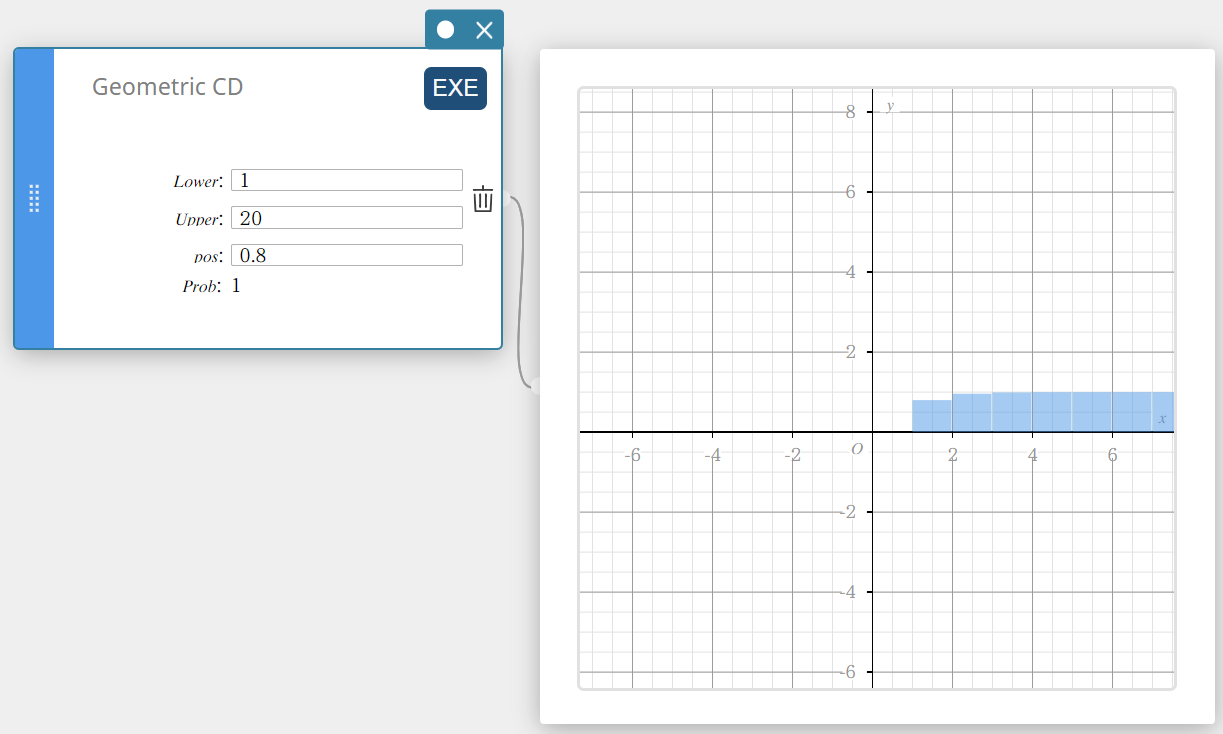
• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  pos : onnistumisen todennäköisyys p (0 \(≤\) p \(≤\) 1)

• Laskettavat termit
  Prob : geometrinen kumulatiivinen todennäköisyys

Hypergeom. PD (Hypergeometrisen jakauman todennäköisyys)
Laskee hypergeometrisen jakauman todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

\( prob = \displaystyle\frac{ {}_MC_x \times {}_{N-M}C_{n-x} }{ {}_NC_n } \)

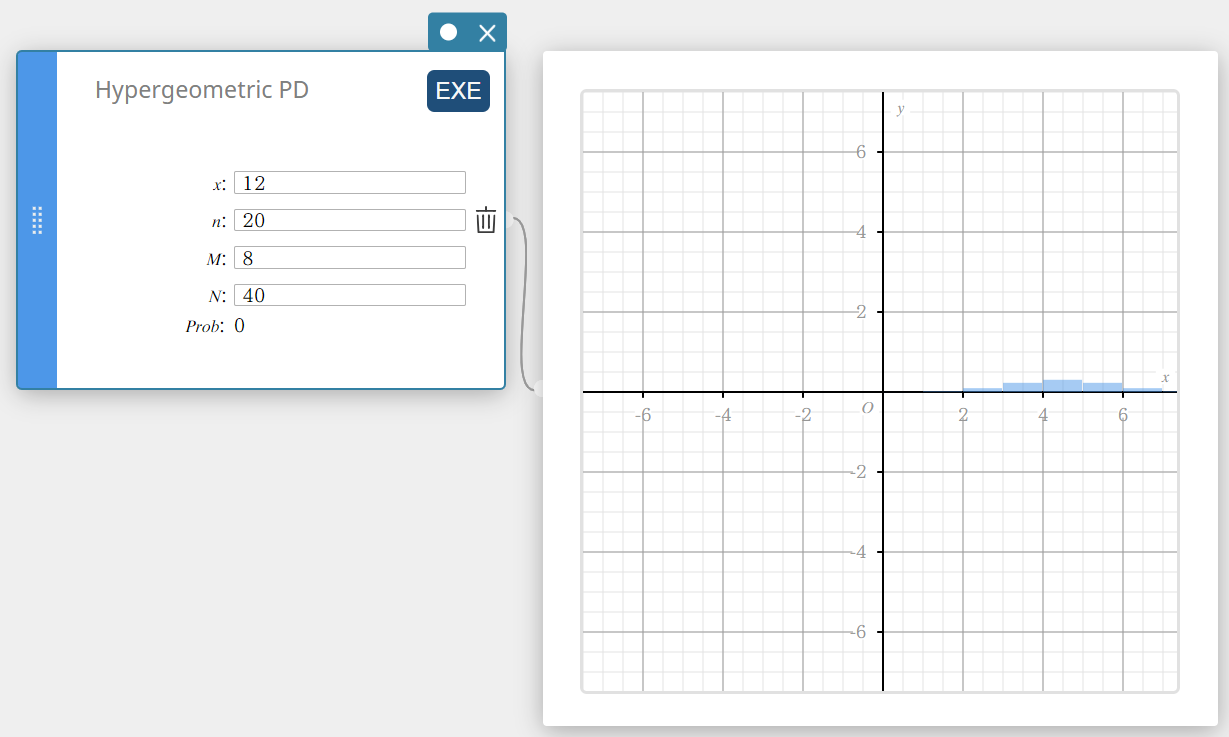
• Syötettävät termit
  \(x\) : tietty koe (kokonaisluku)
  \(n\) : perusjoukosta tehtävien kokeiden lukumäärä (0 \(≤\) n kokonaisluku)
  \(M\) : onnistumisten määrä perusjoukossa (0 \(≤\) M kokonaisluku)
  \(N\) : perusjoukon koko ( n \(≤\) N , M \(≤\) N kokonaisluku)

• Laskettavat termit
  Prob : hypergeometrinen todennäköisyys

Hypergeom. CD (Kumulatiivinen hypergeometrinen jakauma)
Laskee hypergeometrisen jakauman kumulatiivisen todennäköisyyden sille, että onnistuminen tapahtuu tietyssä kokeessa.

\( prob = \sum_{i=Lower}^{Upper}\displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

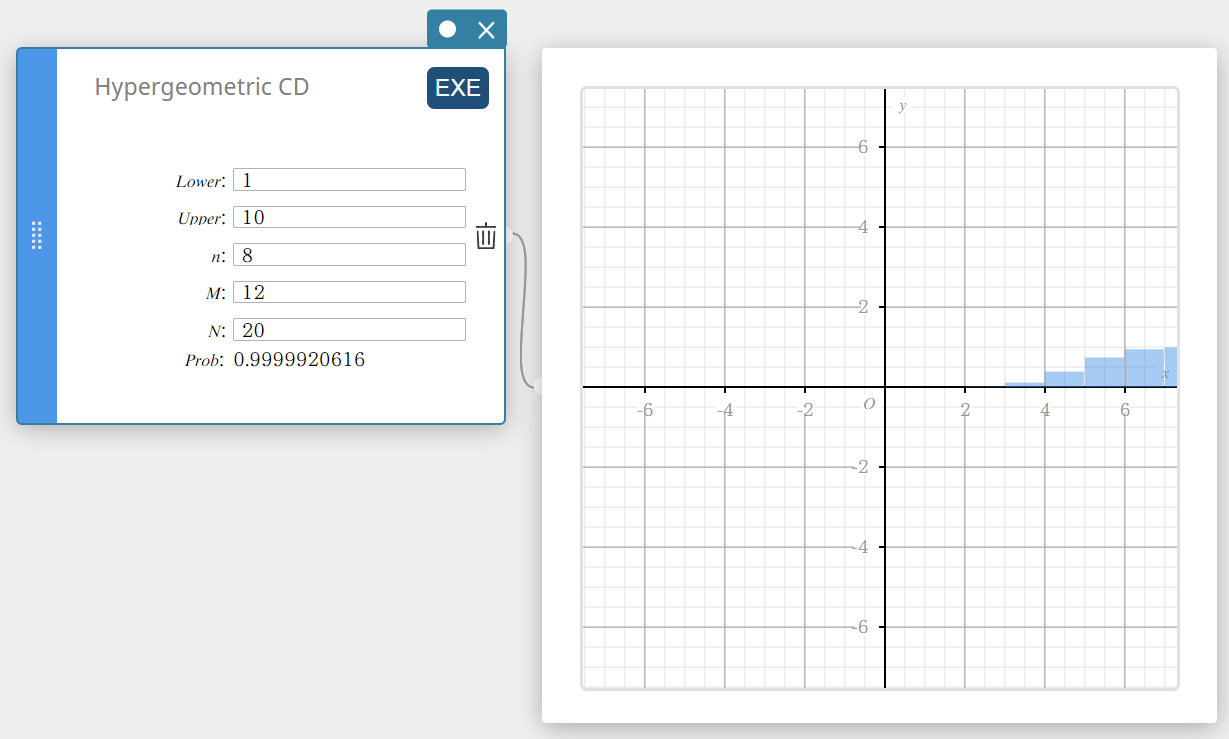
• Syötettävät termit
  Lower : alaraja
  Upper : yläraja
  \(n\) : perusjoukosta tehtävien kokeiden lukumäärä (0 \(≤\) n kokonaisluku)
  \(M\) : onnistumisten määrä perusjoukossa (0 \(≤\) M kokonaisluku)
  \(N\) : perusjoukon koko ( n \(≤\) N , M \(≤\) N kokonaisluku)

• Laskettavat termit
  Prob : hypergeometrinen kumulatiivinen todennäköisyys

Käänt norm CD (Käänteinen normaali kumulatiivinen jakauma)
Laskee normaalijakauman kumulatiivisen todennäköisyyden raja-arvon(-t) tietyille arvoille.

Tail: Left
\( \int_{-\infty}^{\alpha}f(x)dx=p \)
Ylärajan α on palautettu.

Tail: Right
\( \int_{\alpha}^{+\infty}f(x)dx=p \)
Alarajan α on palautettu.

Tail: Keskus
\( \int_{\alpha}^{\beta}f(x)dx=p \qquad \left( \mu=\displaystyle\frac{\alpha+\beta}{2} \right) \)
Alarajan α ja ylärajan β ovat palautettuja.

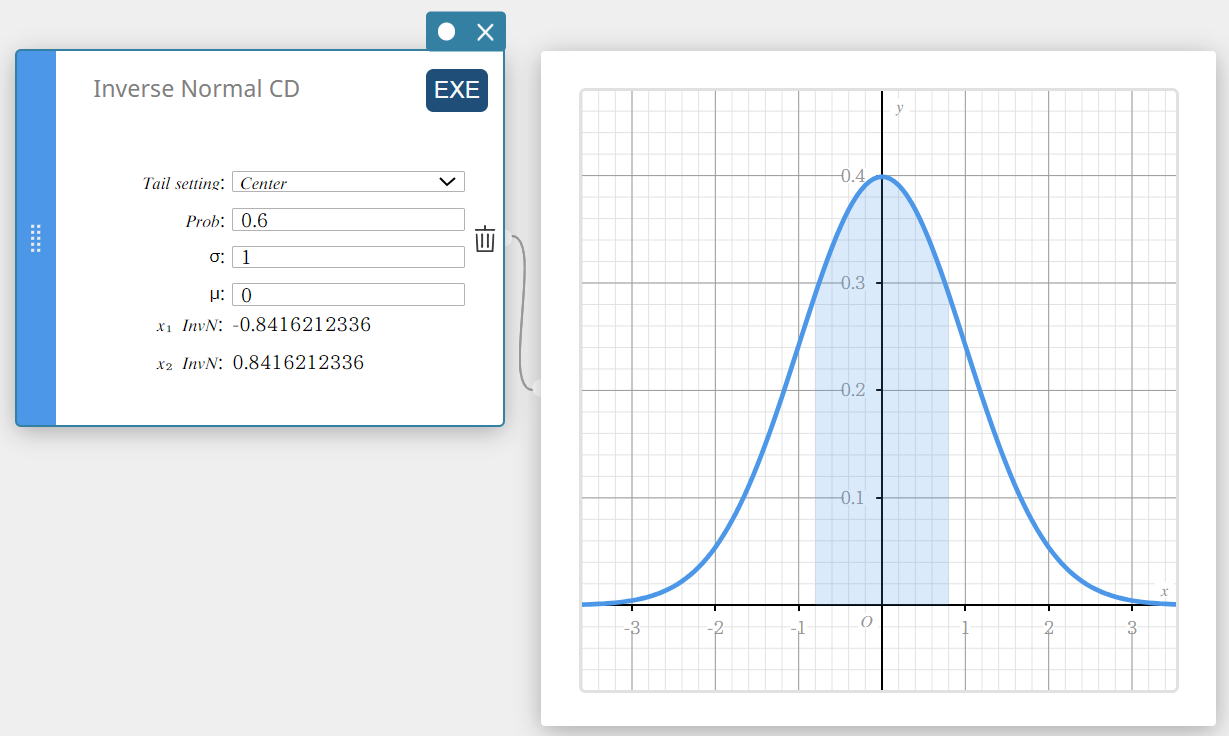
• Syötettävät termit
  Tail -asetus: todennäköisyysarvon suunnan määrittely (Center, Left, Right)
  Prob : todennäköisyysarvo (0 \(≤\) Area \(≤\) 1)
  \( \sigma \) : perusjoukon standardipoikkeama（\( \sigma > 0 \)）
  \( \mu \) : perusjoukon keskiarvo

• Laskettavat termit
  \(x_1 {\rm InvN}\) : Yläraja, kun Tail: Left
       Alaraja, kun Tail: Right tai Tail:Center
  \(x_2 {\rm InvN}\) : Yläraja, kun Tail: Center

Käänt. t CD (Käänteinen Studentin t-kumulatiivinen jakauma)
Laskee Studentin t-kumulatiivisen todennäköisyyden jakauman alaraja-arvon tietyille arvoille.

\( \int_{\alpha}^{+\infty}f(x)=p \)

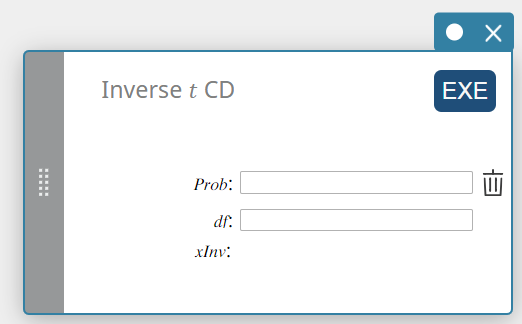
• Syötettävät termit
  Prob : t-kumulatiivinen todennäköisyys (0 \(≤\) Area \(≤\) 1)
  \(df\) : vapausasteet (df > 0)

• Laskettavat termit
  xInv: Studentin t-kumulatiivisen todennäköisyyden jakauman alaraja-arvo

Käänt. \(\chi^2\) CD (Käänteinen \(\chi^2\)-kumulatiivinen binomijakauma)

Laskee \(\chi^2\)-kumulatiivisen todennäköisyyden jakauman alaraja-arvon tietyille arvoille.

\( \int_{\alpha}^{+\infty}f(x)=p \)

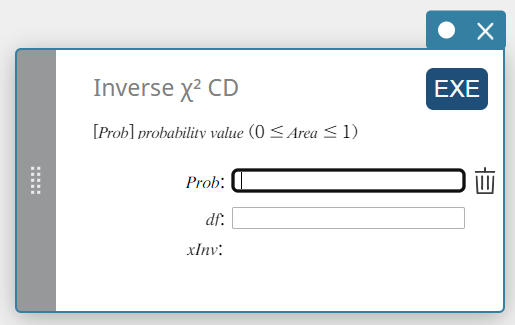
• Syötettävät termit
  Prob : \(\chi^2\)-kumulatiivinen todennäköisyys (0 \(≤\) Area \(≤\) 1)
  \(df\) : vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  \(x {\rm Inv}\) : \(\chi^2\)-kumulatiivisen todennäköisyyden jakauman alaraja-arvo

Käänt. F CD (Käänteinen F-kumulatiivinen jakauma)
Laskee F-kumulatiivisen todennäköisyyden jakauman alaraja-arvon tietyille arvoille.

\( \int_{\alpha}^{+\infty}f(x)=p \)

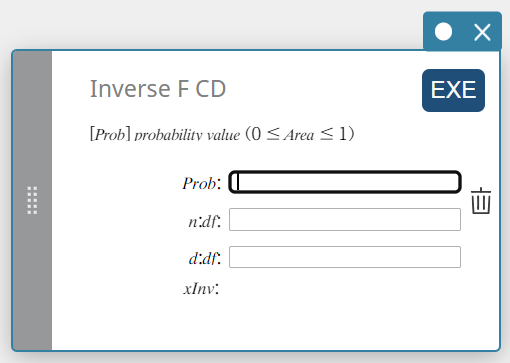
• Syötettävät termit
  Prob : F-kumulatiivinen todennäköisyys (0 \(≤\) Area \(≤\) 1)
  \(n:df\) : osoittajan vapausasteet (positiivinen kokonaisluku)
  \(d:df\) : nimittäjän vapausasteet (positiivinen kokonaisluku)

• Laskettavat termit
  xInv: F-kumulatiivisen todennäköisyyden jakauman alaraja-arvo

Käänt. binomi-CD (Käänteinen kumulatiivinen binomijakauma)
Laskee binomin kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärän tietyille arvoille.

\( \sum_{x=0}^{m}f(x)\ge prob \)

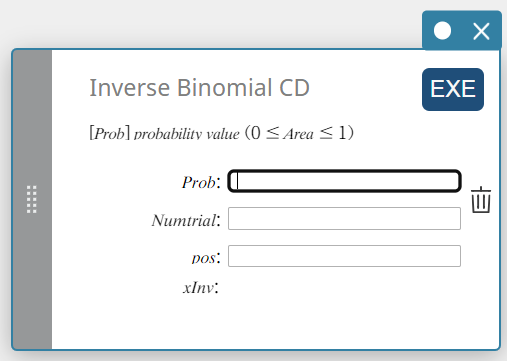
• Syötettävät termit
  Prob : binomin kumulatiivinen todennäköisyys \(\le 1\)）
  Numtrial : kokeiden lukumäärä n (kokonaisluku, n \(≥\) 0)
  pos : onnistumisen todennäköisyys p (0 \(≤\) p \(≤\) 1)

• Laskettavat termit
  xInv : F-kumulatiivisen todennäköisyyden jakauman alaraja-arvo

Käänt. Poisson CD (Käänteinen Poissonin kumulatiivinen jakauma)
Laskee Poissonin kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärän tietyille arvoille.

\( \sum_{x=0}^{m}f(x)\ge prob \)

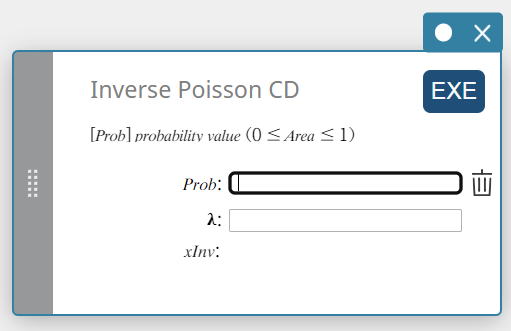
• Syötettävät termit
  Prob : Poissonin kumulatiivinen todennäköisyys（\(0 \le\) Area \(\le 1\)）
  \( \lambda \) : keskiarvo（\(\lambda \gt 0\)）

• Laskettavat termit
  xInv : Poissonin kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärä (ylärajan arvo)

Käänt. Geom. CD (Käänteinen geometrinen kumulatiivinen jakauma)
Laskee geometrisen kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärän tietyille arvoille.

\( \sum_{x=0}^{m}f(x)\ge prob \)

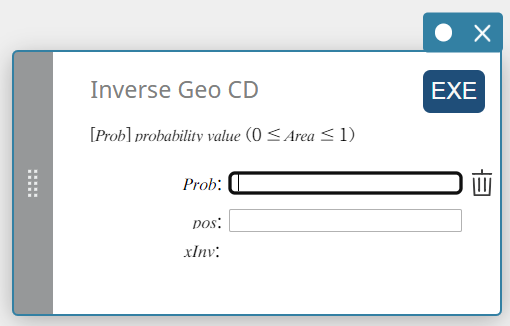
• Syötettävät termit
  Prob : geometrinen kumulatiivinen todennäköisyys（\(0 \le\) Area \(\le 1\)）
  pos : onnistumisen todennäköisyys p（\(0 \le p \le 1\)）

• Laskettavat termit
  xInv : Geometrisen kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärä (ylärajan arvo)

Käänt. hypergeometrin. (Käänteinen hypergeometrinen kumulatiivinen jakauma)
Laskee hypergeometrisen kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärän tietyille arvoille.

\( prob \le \sum_{i=0}^{X} \displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

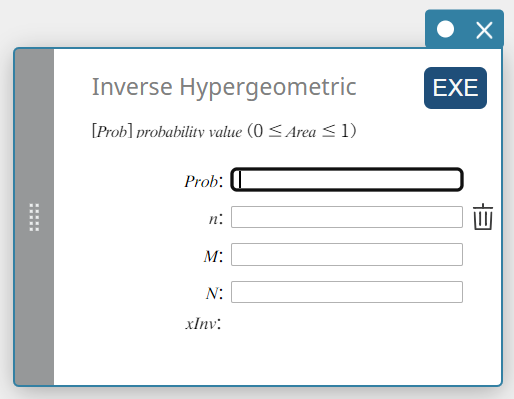
• Syötettävät termit
  Prob : hypergeometrinen kumulatiivinen todennäköisyys（\(0 \le\) Area \(\le 1\)）
  \(n\) : perusjoukosta tehtävien kokeiden lukumäärä (0 \(≤\) n kokonaisluku)
  \(M\) : onnistumisten määrä perusjoukossa (0 \(≤\) M kokonaisluku)
  \(N\) : perusjoukon koko ( n \(≤\) N , M \(≤\) N kokonaisluku)

• Laskettavat termit
  xInv: Hypergeometrisen kumulatiivisen todennäköisyyden jakauman kokeiden minimimäärä (ylärajan arvo)

Muut tilastolliset kuvaajat

Sirontakaavio
Tämä piirros vertailee tietojen kumulatiivista suhdetta normaalin jakauman kumulatiiviseen suhteeseen. Jos sirontakaavio on lähellä suoraa viivaa, tiedot ovat lähellä normaalia. Erkaneminen suorasta viivasta ilmaisee erkanemista normaalista.

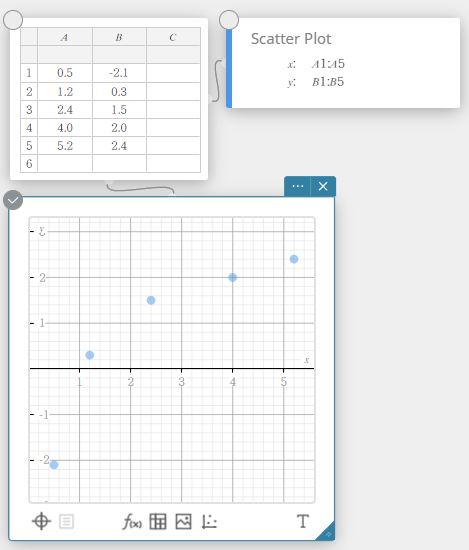
Laatikko-jana-piirros
Tämän tyyppisellä kuvaajalla näet, kuinka suuret määrät tietokohteita ryhmitellään tiettyihin alueisiin. Laatikko sisältää kaikki alueen tiedot ensimmäisestä kvartiilista (\({\rm Q}_1\)) kolmanteen kvartiiliin (\({\rm Q}_3\)), mediaaniin (\({\rm Med}\)) piirretyllä viivalla. Viivat (whiskers) laajenevat boxin molemmista päistä tietojen minimiin (\({\rm minX}\)) ja maksimiin (\({\rm maxX}\)) asti.

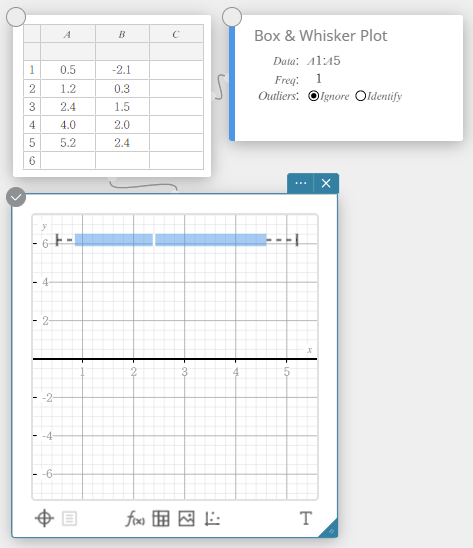
Histogrammi
Histogrammi näyttää kunkin tietoluokan frekvenssin (frekvenssijakauma) suorakulmaisena pylväänä. Luokat ovat horisontaalisella akselilla, ja frekvenssi on vertikaalisella akselilla. Voit tarvittaessa muuttaa histogrammin aloitusarvoa (\(HStart\)) ja askelarvoa (\(HStep\)).

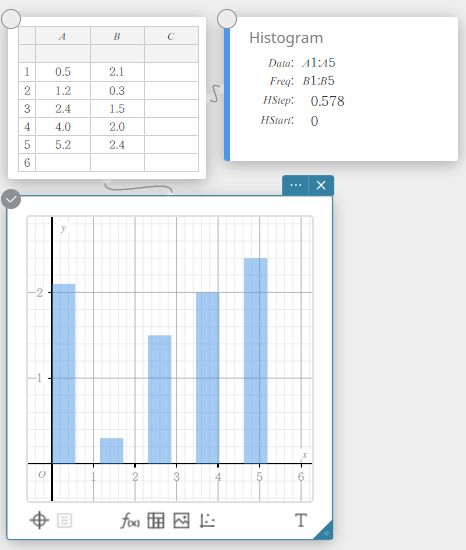
Ympyrädiagrammi
Voit piirtää ympyrädiagrammin perustuen tietyn listan tietoihin.

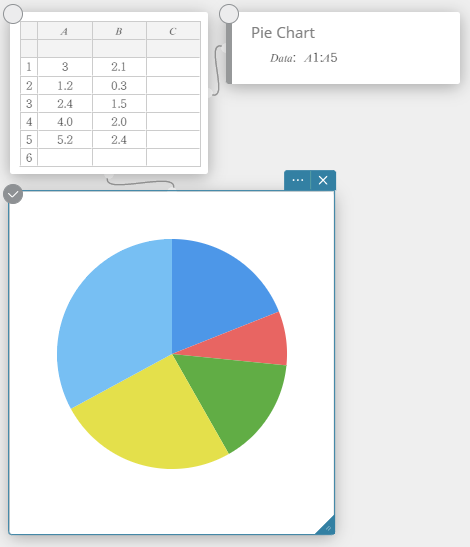
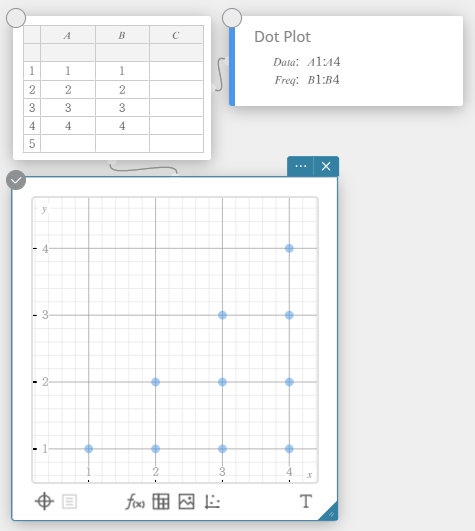
Pistekuvio
Sarakkeen A (horisontaalinen akseli) arvot kuvaavat luokkanumeroita, kun taas sarakkeen B (vertikaalinen akseli) arvot kuvaavat kunkin luokan tietopisteen laskua. Piste asetetaan luokkaan kullekin tietopisteelle.