solve 
Retorna a solução de uma equação ou inequação.
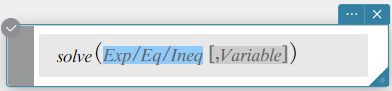
Sintaxe 1: solve(Exp/Eq/Ineq [, Variável] [ ) ]
- “\(x\)” é o padrão quando você omite “[, Variável]”.
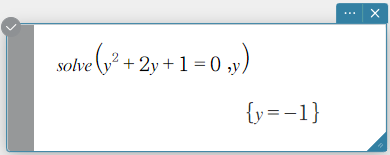
Sintaxe 2: solve(Exp/Eq/Ineq\(≠\), Variável[, valor, limite inferior, limite superior] [ ) ]
- Este comando é válido apenas para equações e expressões \(≠\) quando “valor” e os itens seguintes estão incluídos. Nesse caso, este comando retorna um valor aproximado.
- Um valor verdadeiro é retornado quando você omite “valor” e os itens que o seguem. No entanto, quando um valor verdadeiro não pode ser obtido, um valor aproximado é retornado para equações apenas com base na suposição de que valor = 0, limite inferior = – ∞ e limite superior = ∞.


Sintaxe 3: solve({Exp-1/Eq-1, …, Exp-N/Eq-N}, {Variável-1, …, Variávele-N} [ ) ]
- Quando “Exp” é o primeiro argumento, a equação Exp = 0 é presumida.

Sintaxe 4:
Inserir uma equação vetorial no comando solve( permite que a relação entre 2 objetos (pontos, linhas, planos ou esferas) seja resolvida. Aqui, 4 exemplos típicos de sintaxe são mostrados para resolver uma equação vetorial usando o comando solve(.
A sintaxe abaixo mostra um vetor coluna com 3 (ou 2) elementos entre Vct-1 e Vct-6), com s, t, u e v como parâmetros.
solve(Vct-1 + s * Vct-2 [= Vct-3, {Variável-1}])
- Se o lado direito da equação (= Vct-3) for omitido na sintaxe acima, assume-se que todos os elementos do lado direito são 0 vetores.
solve(Vct-1 + s * Vct-2 = Vct-3 + t * Vct-4, {Variável-1, Variável-2})
solve(Vct-1 + s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5, {Variável-1, Variável-2, Variável-3})
solve(Vct-1 + s* Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5 + v * Vct-6, {Variável-1, Variável-2, Variável-3, Variável-4}) - Variáveis (variável 1 a variável 4) podem ser inseridas nos elementos de cada vetor (Vct-1 a Vct-6) nas quatro sintaxes acima para resolver essas variáveis.

dSolve 
Resolve equações diferenciais ordinárias de primeira, segunda ou terceira ordem, ou um sistema de equações diferenciais de primeira ordem.
Sintaxe: dSolve(Eq, variável independente, variável dependente [, condição inicial-1, condição inicial-2][, condição inicial-3, condição inicial-4][, condição inicial-5, condição inicial-6][ ) ]
dSolve({Eq-1, Eq-2}, independent variable, {dependent variable-1, dependent variable-2} [, initial condition-1, initial condition-2, initial condition-3, initial condition-4] [ ) ]
- Se você omitir as condições iniciais, a solução incluirá constantes arbitrárias.
- Insira todas as equações de condições iniciais usando a sintaxe Var = Exp. Qualquer condição inicial que utilize qualquer outra sintaxe será ignorada.


taylor 
Encontra um polinômio de Taylor para uma expressão em relação a uma variável específica.
Sintaxe: taylor (Exp/List, Variable, ordem [, ponto central] [ ) ]
- Zero é o padrão quando você omite “[, ponto central]”.

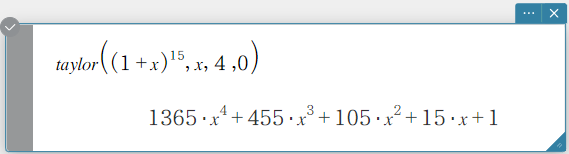
laplace, invLaplace 
“laplace” é o comando para a transformada de Laplace e “invLaplace” é o comando para o inverso da transformada de Laplace.
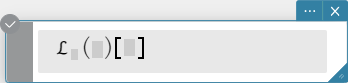
Sintaxe: laplace \(\mathcal{L}_t (f(t))[s]\)
\(f(t)\): Fórmula
\(t\): Variável em relação à qual a expressão é transformada
\(s\): parâmetro da transformação
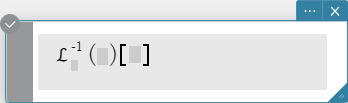
invLaplace \(\mathcal{L}_s^{-1} (L(s))[t]\)
\(L(s)\): Fórmula
\(s\): Variável em relação à qual a expressão é transformada
\(t\): parâmetro da transformação
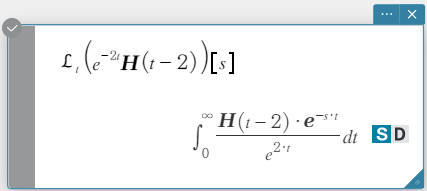
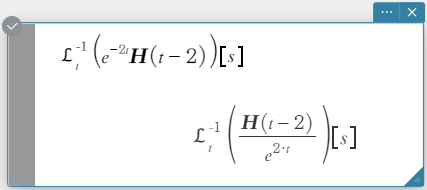
fourier, invFourier 
“fourier” é o comando para a transformada de Fourier e “invFourier” é o comando para a transformada inversa de Fourier.
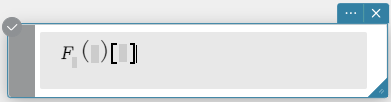
Sintaxe: fourier \(~ Ϝ_x (f(x))[w]\)
invFourier \(~ Ϝ_w^{-1} (f(w))[x]\)
\(x\): Variável em relação à qual a expressão é transformada
\(w\): parâmetro da transformação
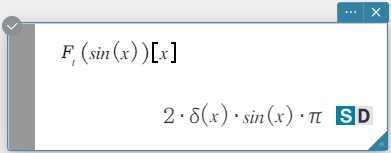

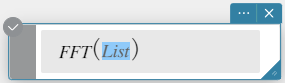
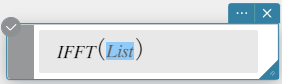
FFT, IFFT 
“FFT” é o comando para a transformada rápida de Fourier e “IFFT” é o comando para a transformada rápida inversa de Fourier.
O valor de dados \(2^n\) é necessário para executar FFT e IFT. FFT e IFFT são calculados numericamente.
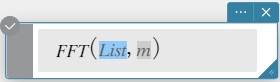
Sintaxe: FFT(list) ou FFT(list, m)
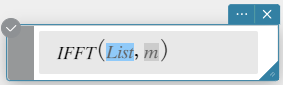
IFFT(list) ou IFFT(list, m)
- O tamanho dos dados deve ser \(2^n\) para n = 1, 2, 3, …
- O valor para m é opcional. Pode ser de 0 a 2, indicando o parâmetro FFT a ser utilizado: 0 (Processamento de Sinal), 1 (Matemática Pura), 2 (Análise de Dados).