Cálculos estatísticos

índice

Operações básicas de cálculo estatístico
Editando valores de dados estatísticos
Selecionando valores de dados para cálculo estatístico
Realizando cálculos estatísticos de uma variável
Desenhando um gráfico de regressão
Desenhando um histograma
Desenhando um diagrama de caixa e bigode
Desenhando um gráfico circular
Operações de gráfico de dispersão
Realizando um teste Z de uma amostra
Cálculos estatísticos e gráficos

Operações básicas de cálculo estatístico

• Para inserir valores em uma nota adesiva de dados estatísticos
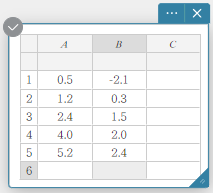
  No exemplo mostrado nesta seção, os valores dos dados na tabela abaixo são inseridos nas células A1 a B5 de uma nota adesiva de Dados Estatísticos.

	A	B
1	\(0.5\)	\(-2.1\)
2	\(1.2\)	\(0.3\)
3	\(2.4\)	\(1.5\)
4	\(4.0\)	\(2.0\)
5	\(5.2\)	\(2.4\)

1. Clique no cardápio de notas adesivas.
   
   Isso exibe uma nota adesiva de dados estatísticos.
   
   A célula A1 é selecionada para entrada neste momento.
2. Digite \(0.5\) na célula A1 e pressione [Enter].
   A célula A2 é selecionada para entrada.
3. Digite \(1.2\) na célula A2 e pressione [Enter].
   A célula A3 é selecionada para entrada. Da mesma forma, insira os dados até a célula A5.
4. Clique na célula B1.
   A célula B1 é selecionada para entrada.
5. Digite \(-2.1\) na célula B1 e pressione [Enter].
   A célula B2 é selecionada para entrada. A coluna C também é criada neste ponto (ver MEMORANDO abaixo).
6. Digite \(0.3\) na célula B2 e pressione [Enter].
   A célula B3 é selecionada para entrada. Da mesma forma, insira os dados até a célula B5.　　
   
   MEMORANDO
   Inserir um valor na coluna mais à direita adiciona automaticamente uma nova coluna à direita dela.
   
   As células sob os rótulos das colunas (A, B, C,…) podem ser usadas para inserir um nome de lista para cada coluna. Para obter detalhes, consulte “Atribuindo um nome a uma lista”.

• Seleção de valores de dados para cálculo estatístico

1. Use o procedimento em “Inserindo valores em uma nota adesiva de dados estatísticos” para inserir valores de dados.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)

2. Use o mouse do computador para arrastar da célula A1 para a célula B5.
   Isso seleciona o intervalo de células da célula A1 até a célula B5.
   
   MEMORANDO
   Você pode selecionar uma coluna inteira clicando no número da coluna.
   Você pode selecionar uma linha inteira clicando no número da linha.
   Você pode clicar ou arrastar os números das colunas e usar os dados dessas colunas para desenhar um gráfico.
   Nesse caso, após desenhar o gráfico, você também pode usar a lista suspensa da nota adesiva do gráfico para selecionar outros números de coluna e redesenhar o gráfico.
   

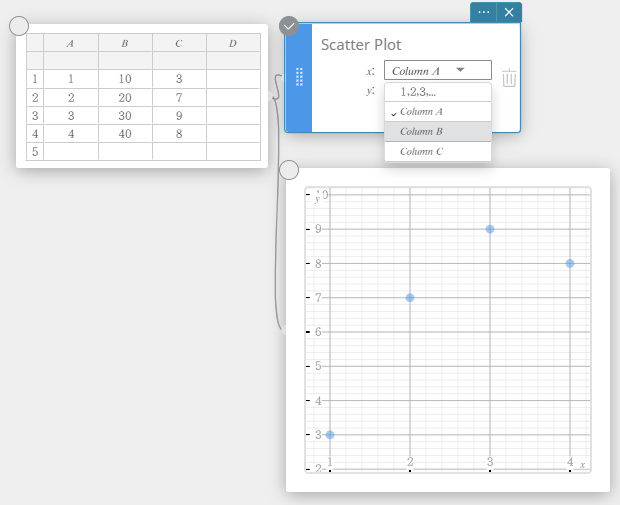
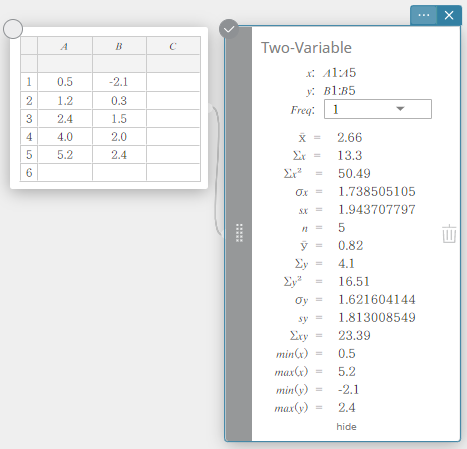
• Realização de cálculos estatísticos

Neste exemplo, realizamos cálculos estatísticos de duas variáveis e desenhamos um gráfico de dispersão e um gráfico de regressão linear.

1. Insira os valores dos dados na tabela abaixo e selecione todos os dados.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)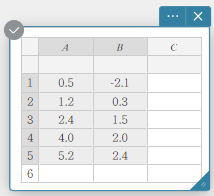

   

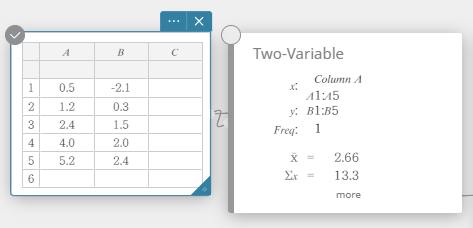
2. No teclado do Programas, clique em [Cálculo] – [Duas variáveis].
   
   Isso exibe resultados de cálculos estatísticos de duas variáveis.
   
3. Clique no teclado do Programas.
   
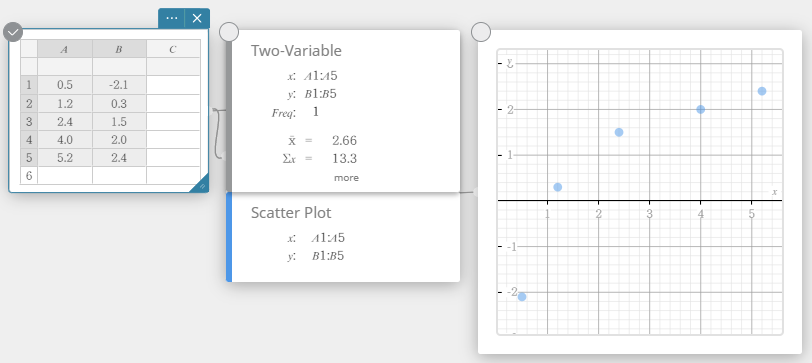
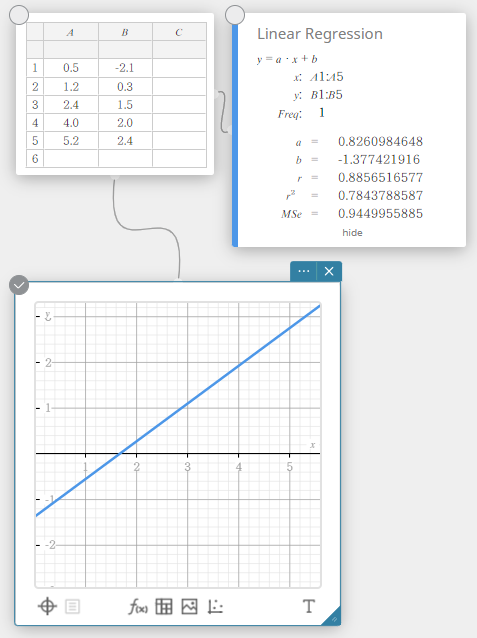
4. No teclado do Programas, clique em [Gráfico] – [Gráfico de dispersão].
   
   Isso cria uma nota adesiva do gráfico de dispersão e simultaneamente desenha um gráfico de dispersão na nota adesiva do gráfico.
   
5. Clique no teclado do Programas.
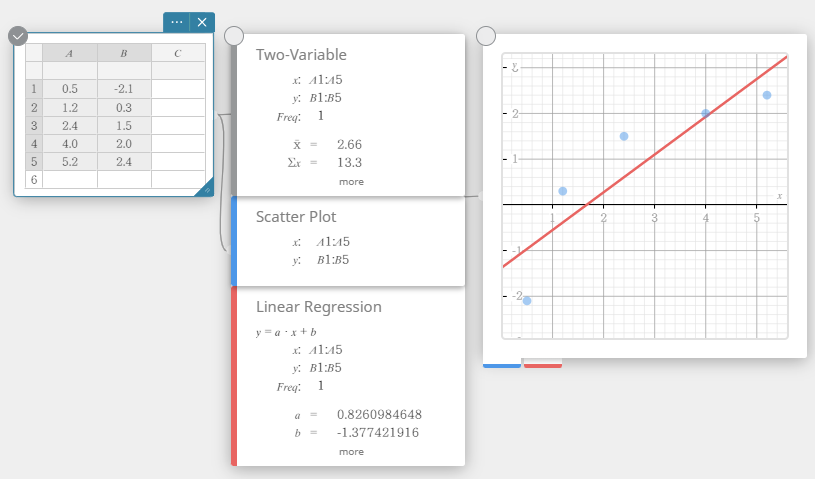
6. No teclado do Programas, clique em [Regressão] – [Regressão linear].
   
   Isso cria uma nota adesiva de regressão linear e simultaneamente desenha um gráfico de regressão linear na nota adesiva do gráfico.
   

Editando valores de dados estatísticos

• Para corrigir valores de dados

1. Clique na célula que contém o valor dos dados que deseja corrigir.
   
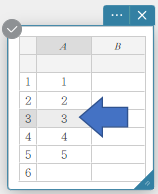
2. Insira o novo valor dos dados e pressione [Enter].
   

• Para inserir uma linha

1. Clique com o botão direito no número da linha onde deseja inserir uma nova linha.
   Isso exibe um cardápio.
   
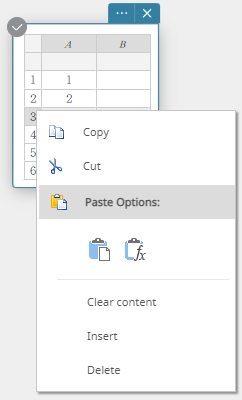
2. Clique [Inserir].
   Isso insere uma linha.
   

• Para inserir uma coluna

1. Clique com o botão direito no cabeçalho da coluna onde deseja inserir uma nova coluna.
   Isso exibe um cardápio.
   
2. Clique [Inserir].
   Isso insere uma coluna.
   

• Para excluir uma linha

1. Clique com o botão direito no número da linha que deseja excluir.
   Isso exibe um cardápio.
   
2. Clique [Excluir].
   Isso exclui a linha.
   

• Para excluir uma coluna

1. Clique com o botão direito no cabeçalho da coluna que deseja excluir.
   Isso exibe um cardápio.
   
2. Clique [Excluir].
   Isso exclui a coluna.
   

• Atribuindo um nome a uma lista

Depois de atribuir um nome a uma lista, você poderá usá-lo em testes e outros cálculos estatísticos. Os nomes das listas são inseridos nas células abaixo dos nomes das colunas.

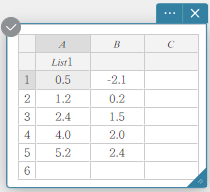
Exemplo: Para atribuir o nome “Lista1” à coluna A

1. Clique duas vezes na célula abaixo de A.
   Isso seleciona a célula para entrada do nome da lista.
   
2. Insira o nome da lista “Lista1” e pressione [Enter].
   Isso atribui “Lista1” como o nome da lista da coluna A.
   
   MEMORANDO
   As regras a seguir se aplicam a nomes de listas.
   － Os nomes das listas podem ter até 8 bytes de comprimento.
   － Os seguintes caracteres são permitidos em um nome de lista: caracteres maiúsculos e minúsculos, caracteres subscritos, números.
   － Os nomes das listas diferenciam maiúsculas de minúsculas. Por exemplo, cada um dos itens a seguir é tratado como um nome de lista diferente: abc, Abc, aBc, ABC.

Selecionando valores de dados para cálculo estatístico

Você pode selecionar um intervalo de células arrastando o ponteiro do rato sobre elas.

Exemplos de seleção de dados

MEMORANDO
Você pode selecionar uma coluna inteira clicando no número da coluna.
Você pode selecionar uma linha inteira clicando no número da linha.

Cálculos estatísticos poderão ser realizados se o intervalo de células selecionadas incluir uma ou mais células em branco.
Até três colunas podem ser usadas para cálculos estatísticos. Cálculos estatísticos não poderão ser realizados se mais de três colunas forem selecionadas.

Realizando cálculos estatísticos de uma variável

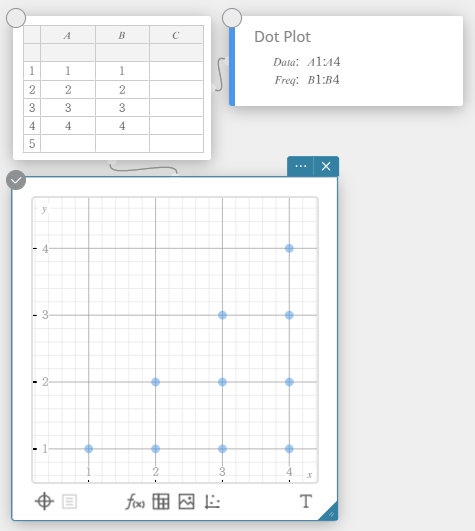
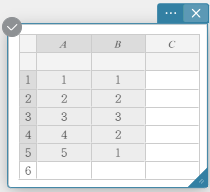
1. Insira os valores dos dados na tabela abaixo, com dados na coluna A e frequência na coluna B.
   

   Dados	Frequência
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Arraste da célula A1 para a célula B5 para selecionar o intervalo de células entre elas.
   

3. No teclado do software, clique em [Cálculo] – [Uma variável].
   Isso exibe resultados de cálculos estatísticos de uma variável.
   
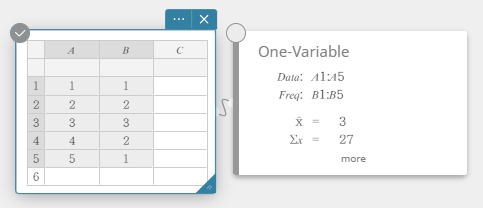
4. Para exibir outros itens de resultados de cálculo ocultos, clique em [mais] na nota adesiva de Cálculo Estatístico.
   Isso exibe os resultados ocultos do cálculo.
   Para retornar a nota adesiva de Cálculo Estatístico à sua configuração de tamanho reduzido, clique em [ocultar].
   

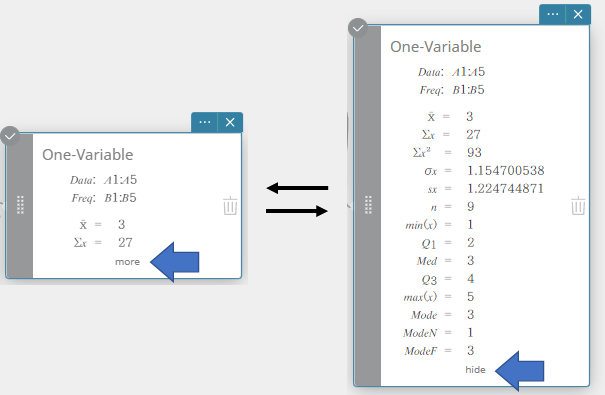
A execução de um cálculo estatístico de uma variável exibe os resultados abaixo.
\(\bar{\rm x}\)　　　média da amostra
\(\Sigma {\rm x}\)　　 soma de dados
\(\Sigma {\rm x}^2\)　　 soma dos quadrados
\(\sigma {\rm x}\)　　　desvio padrão da população
\({\rm sx}\)　　　 desvio padrão da amostra
\({\rm n}\)　　　　tamanho da amostra
\({\rm min(x)}\)　mínimo
\({\rm Q}_1\)　　　primeiro quartil
\({\rm Med}\)　　 Mediana
\({\rm Q}_3\)　　　 terceiro quartil
\({\rm max(x)}\)　máximo
\({\rm Mode}\)　　modo
\({\rm ModeN}\)　 número de itens do modo de dados
\({\rm ModeF}\)　frequência do modo de dados
Quando \({\rm Mode}\) tem múltiplas soluções, todas elas são exibidas.

Desenhando um gráfico de regressão

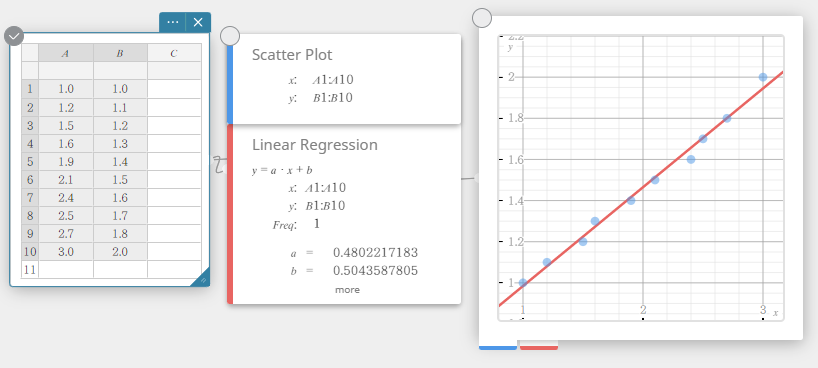
Neste exemplo, usaremos os valores dos dados abaixo para desenhar um gráfico de dispersão, um gráfico de regressão linear e um gráfico de regressão quadrática.

1. Insira os valores dos dados na tabela abaixo e selecione todos os dados.
   

   A	B
   \(1.0\)	\(1.0\)
   \(1.2\)	\(1.1\)
   \(1.5\)	\(1.2\)
   \(1.6\)	\(1.3\)
   \(1.9\)	\(1.4\)
   \(2.1\)	\(1.5\)
   \(2.4\)	\(1.6\)
   \(2.5\)	\(1.7\)
   \(2.7\)	\(1.8\)
   \(3.0\)	\(2.0\)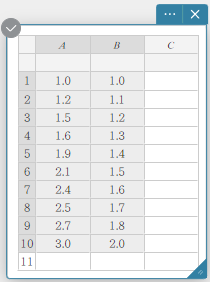

   

2. No teclado do Programas, clique em [Gráfico] – [Gráfico de dispersão].
   
   Isso cria uma nota adesiva do gráfico de dispersão e simultaneamente desenha um gráfico de dispersão na nota adesiva do gráfico.
   
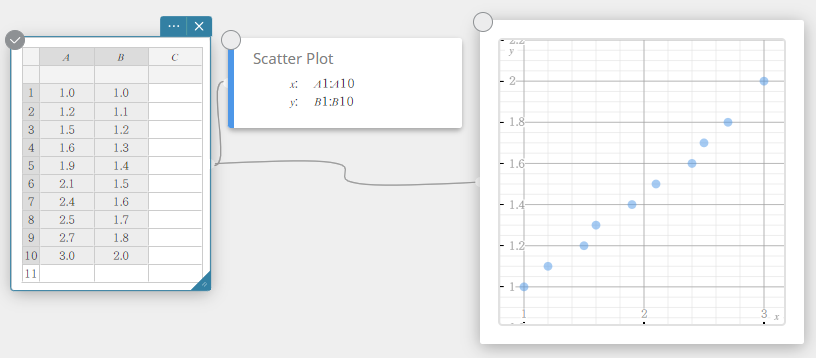
3. Clique no teclado do Programas.
   
4. No teclado do Programas, clique em [Regressão] – [Regressão linear].
   
   Isso cria uma nota adesiva de regressão linear e simultaneamente desenha um gráfico de regressão linear na nota adesiva do gráfico.
   
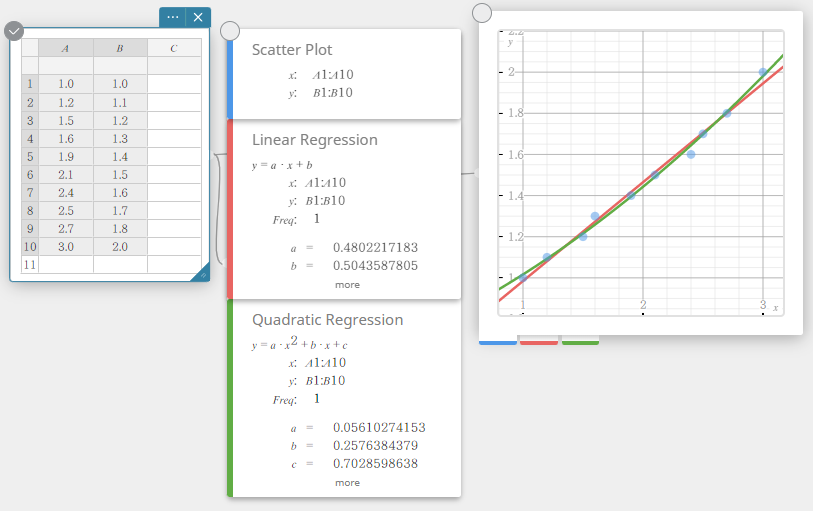
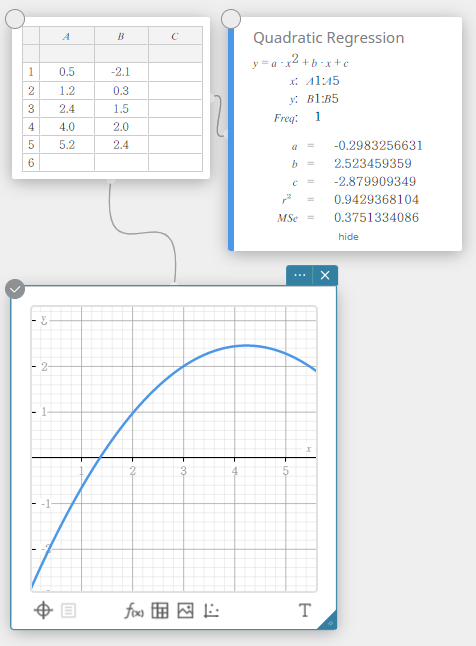
5. No teclado do Programas, clique em [Regressão Quadrática].
   
   Isso cria uma nota adesiva de regressão quadrática e simultaneamente desenha um gráfico de regressão quadrática na nota adesiva do gráfico.
   

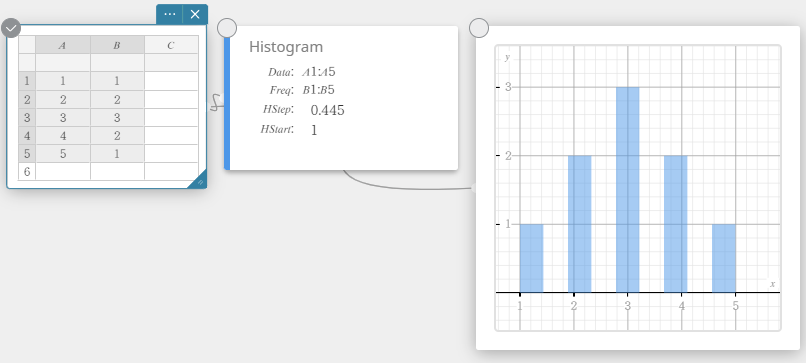
Desenhando um histograma

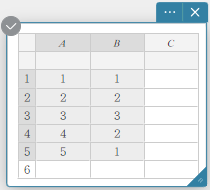
1. Insira os valores dos dados na tabela abaixo, com dados na coluna A e frequência na coluna B.
   

   Dados	Frequência
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Arraste da célula A1 para a célula B5 para selecionar o intervalo de células entre elas.
   

3. No teclado do Programas, clique em [Gráfico] – [Histograma].
   Isso cria uma nota adesiva do histograma e simultaneamente desenha um histograma na nota adesiva do gráfico.
   
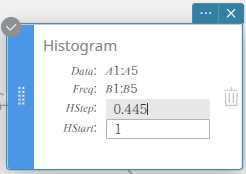
   MEMORANDO
   Você pode alterar o valor inicial do desenho do histograma (HIniciar) e o valor do passo (HSetapa). Na nota adesiva do histograma, clique em HIniciar ou HSetapa e insira o valor desejado.
   

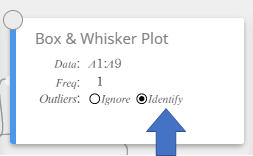
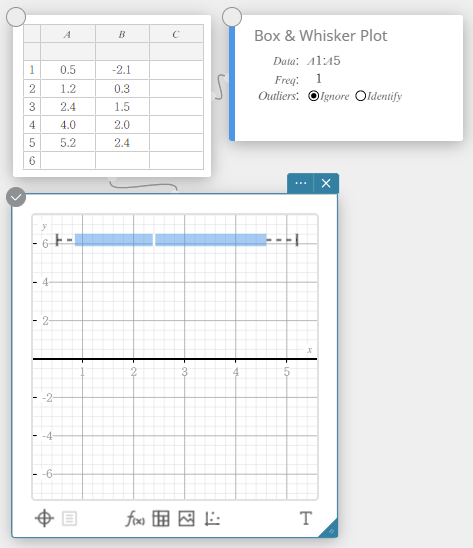
Desenhando um diagrama de caixa e bigode

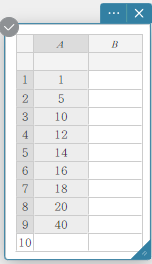
1. Insira os valores dos dados na tabela abaixo na coluna A.
   

   A
   \(1\)
   \(5\)
   \(10\)
   \(12\)
   \(14\)
   \(16\)
   \(18\)
   \(20\)
   \(40\)

2. Arraste da célula A1 para a célula A9 para selecionar o intervalo de células entre elas.
   

3. No teclado do Programas, clique em [Gráfico] – [Gráfico de caixa e bigode].
   Isso cria uma nota adesiva de gráfico de caixa e bigode e simultaneamente desenha um diagrama de caixa e bigode na nota adesiva do gráfico.
   
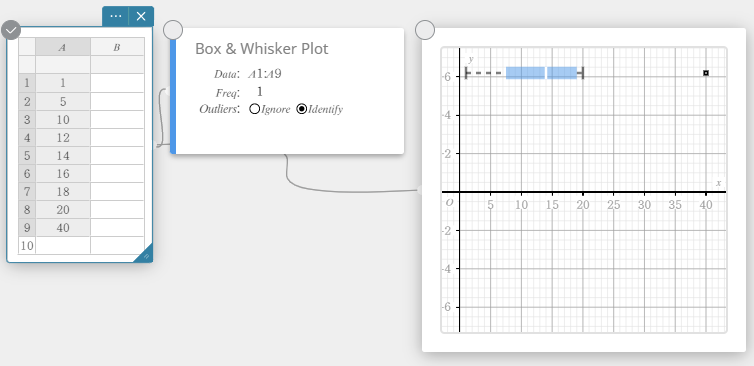
   MEMORANDO
   Você pode exibir valores discrepantes. Para fazer isso, selecione [Identificar] para o item Outliers do nota adesiva Gráfico de caixa e bigode.
   

Desenhando um gráfico circular

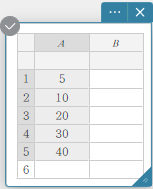
1. Insira os valores dos dados na tabela abaixo na coluna A.
   

   A
   \(5\)
   \(10\)
   \(20\)
   \(30\)
   \(40\)

2. Arraste da célula A1 para a célula A5 para selecionar o intervalo de células entre elas.
   

3. No teclado do Programas, clique em [Gráfico] – [Gráfico de pizza].
   Isso cria uma nota adesiva de gráfico de pizza e simultaneamente desenha um gráfico de pizza em uma nota adesiva separada*.
   
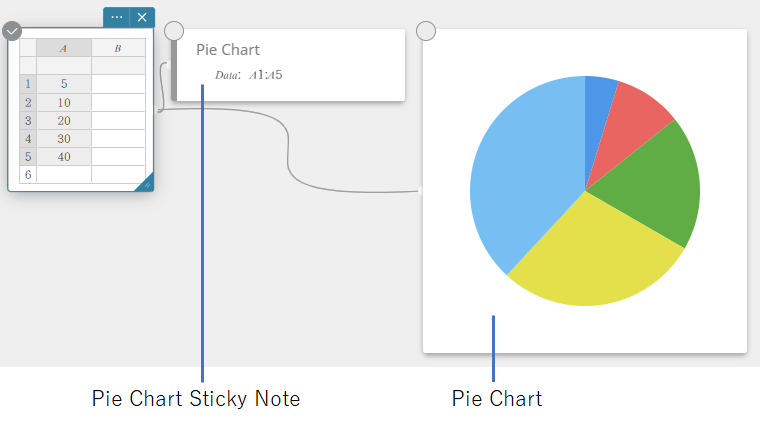
   *　Isso desenha o gráfico na nota adesiva do Gráfico. O tipo é diferente quando um gráfico circular é desenhado no nota adesiva.

Operações de gráfico de dispersão

• Para mover os pontos de um gráfico de dispersão

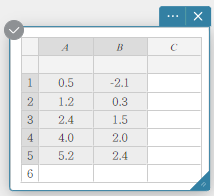
1. Insira os valores dos dados da tabela abaixo nas colunas A e B.
   

   Dados	Frequência
   \(0.5\)	\(-2.1\)
   \(1.2\)	\(0.3\)
   \(2.4\)	\(1.5\)
   \(4.0\)	\(2.0\)
   \(5.2\)	\(2.4\)

2. Arraste da célula A1 para a célula B5 para selecionar o intervalo de células entre elas.
   

3. No teclado do Programas, clique em [Gráfico] – [Gráfico de dispersão].
   Isso cria uma nota adesiva de gráfico de dispersão e uma nota adesiva de gráfico, e desenha um gráfico de dispersão na nota adesiva de gráfico.
   
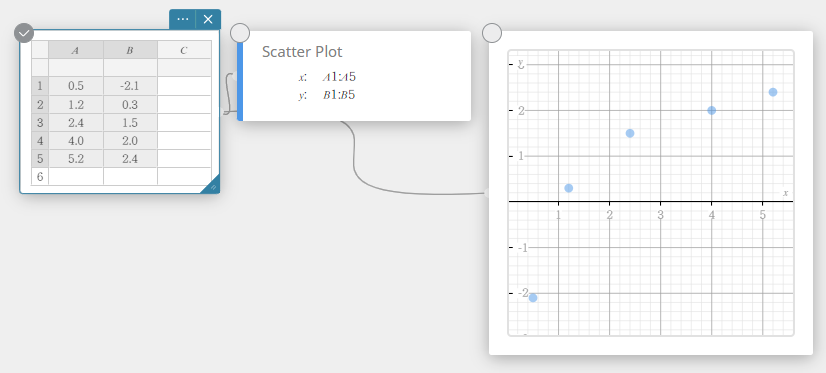
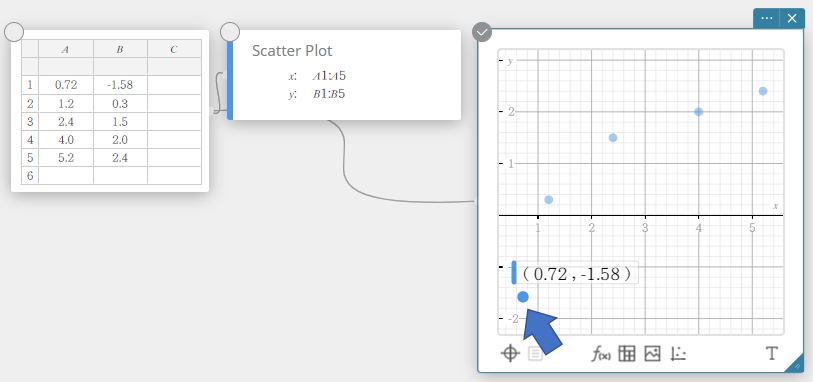
4. Para mover um ponto do gráfico de dispersão, arraste-o.
   Isso também alterará os valores das notas adesivas dos Dados Estatísticos para as coordenadas do destino.
   

• Para bloquear uma célula

MEMORANDO
Quando uma célula está bloqueada, seu valor de dados não será alterado, mesmo se você tentar mover o ponto do gráfico de dispersão. Por exemplo, se você bloquear uma célula da coluna A, o ponto do gráfico de dispersão correspondente não poderá ser movido ao longo do eixo x.

1. Continuando com o procedimento descrito em “Para mover os pontos de um gráfico de dispersão”, selecione a célula A1.
2. Clique no notas adesivas de Cálculo Estatístico.
   
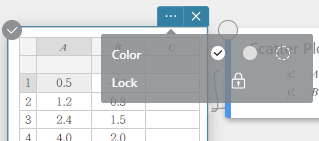
3. Clique no ícone ao lado [Bloquear].
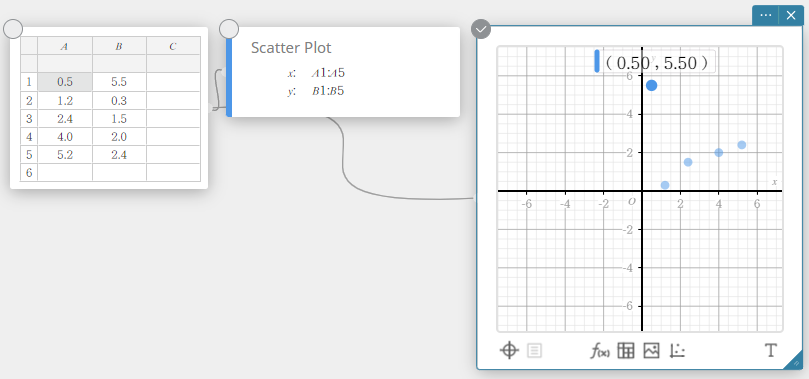
   Isso bloqueia as células A1. Se você arrastar o ponto do gráfico de dispersão que corresponde às células A1 e B1, o movimento ao longo do eixo x não será possível.
   

• Para desbloquear uma célula

1. Selecione a célula bloqueada que deseja desbloquear.
2. Clique no nota adesiva de Cálculo Estatístico.
   
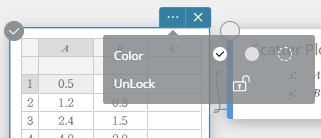
3. Clique no ícone ao lado [Desbloquear].

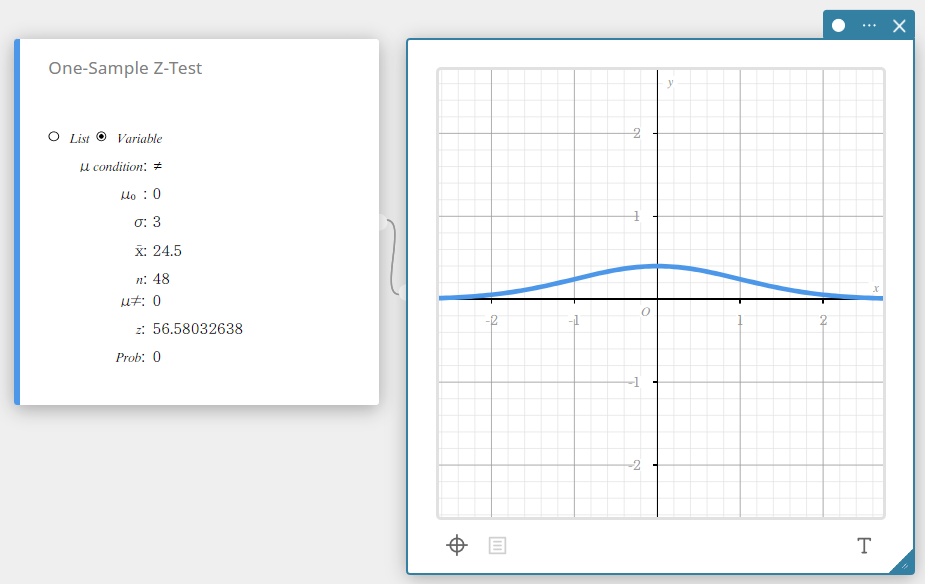
Realizando um teste Z de uma amostra

• Para especificar o número de amostras de dados e, em seguida, realizar um teste Z de uma amostra

Exemplo:
Tamanho da amostra: \(n=48\)
Média da amostra: \(\overline{x}=24.5\)
Hipótese nula: \(\mu \ne 0\)
Desvio padrão: \(\sigma=3\)

1. Crie uma nota adesiva de dados estatísticos.
2. No teclado do Programas, clique em [Teste] – [Teste Z de uma amostra].
   
   Isso cria uma nota adesiva de teste Z de uma amostra.
   
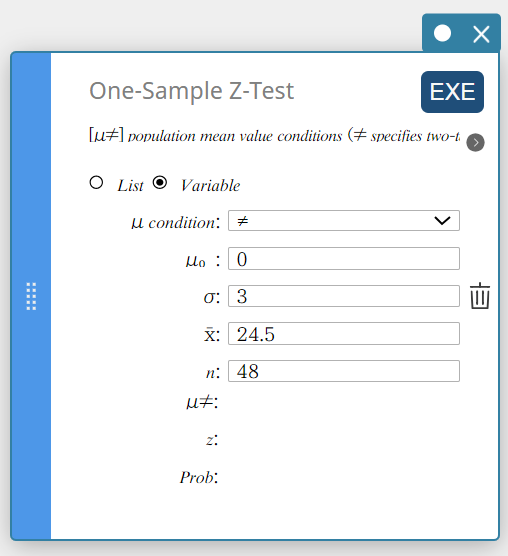
3. Defina as configurações conforme mostrado abaixo.
   \(\mu\) condição: No menu que aparece, selecione “\(\ne\)”.
   \(\mu_0\) : Entrada \(0\).
   \(\sigma\): Entrada \(3\).
   \(\overline{x}\) : Entrada \(24.5\).
   \(n\) : Entrada \(48\).
   
4. Clique [EXE].
   
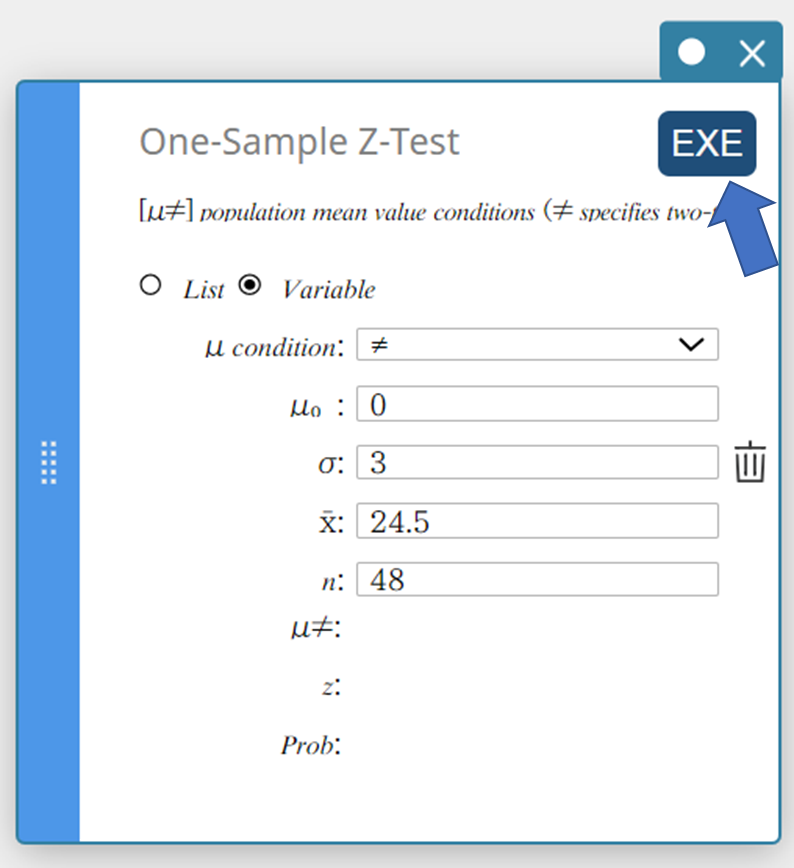
   Isso exibe os resultados do cálculo e o gráfico.
   
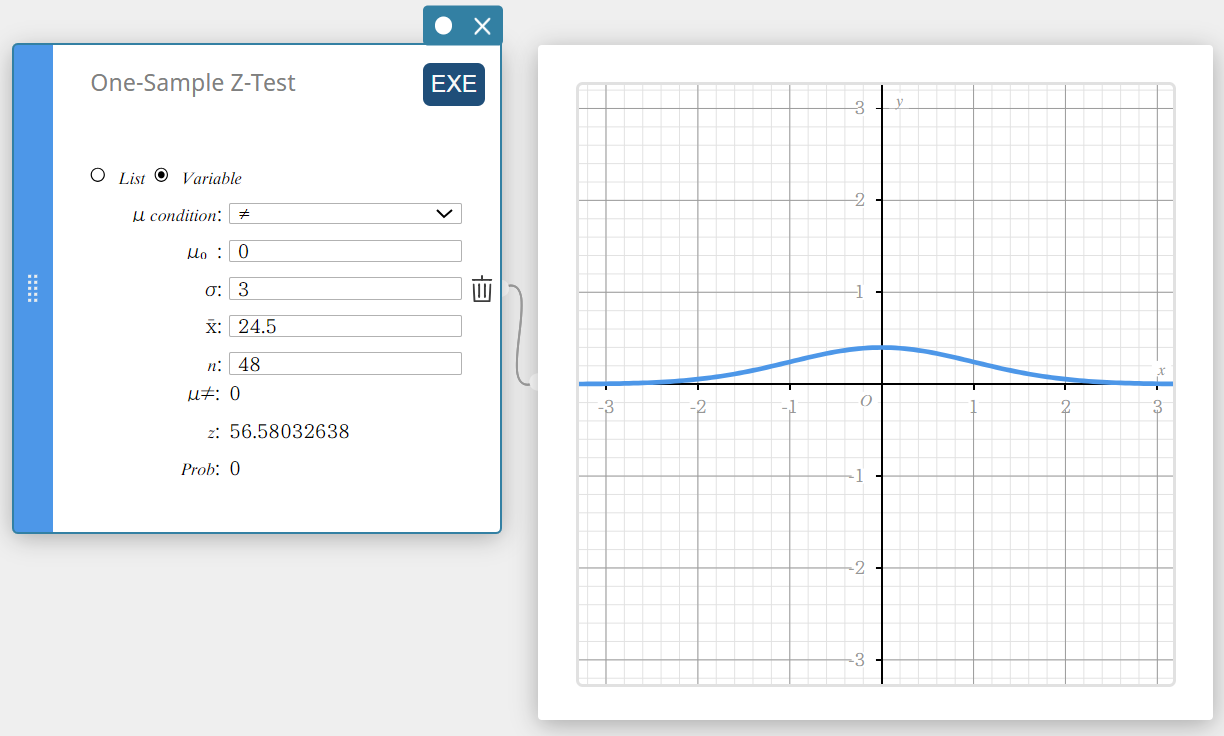
   \(\mu \ne\) condição de valor médio da população
   \(\rm z\) 　　\(\rm z\) valor
   Problema 　\(\rm p\) valor
   \(\overline{x}\) 　　média da amostra
   \(n\) 　　tamanho da amostra

• Para usar listas para realizar um teste Z de uma amostra

1. Insira os seguintes nomes de lista: Lista 1 para coluna A, Lista 2 para coluna B.
2. Insira o valor dos dados na tabela abaixo.
   
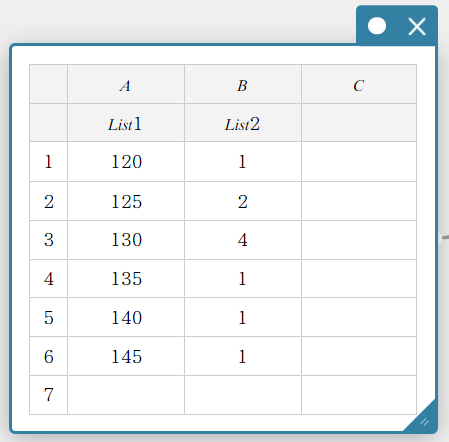
3. Arraste da célula A1 para a célula B6 para selecionar o intervalo de células.
4. No teclado do Programas, clique em [Teste] – [Teste Z de uma amostra].
   
   Isso cria uma nota adesiva de teste Z de uma amostra.
   
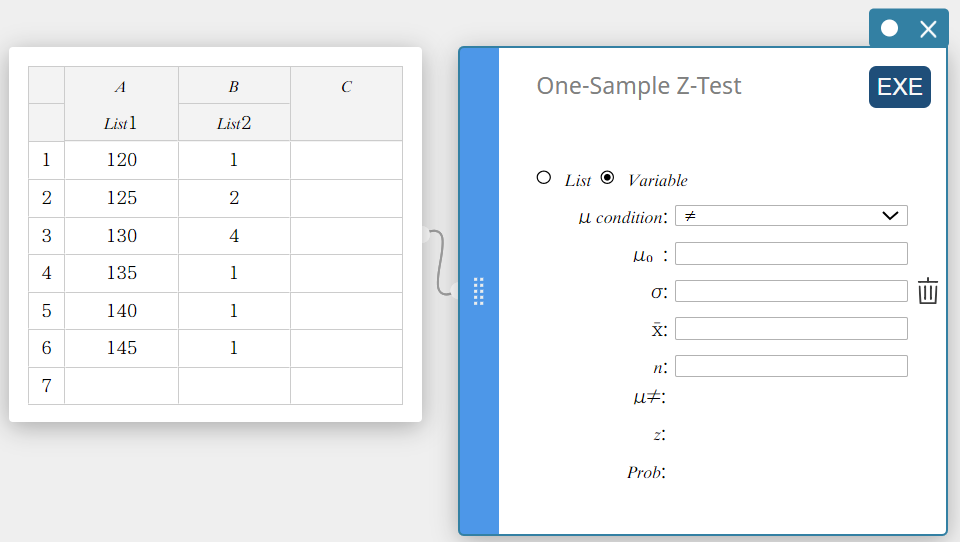
5. Clique em “Lista”.
   
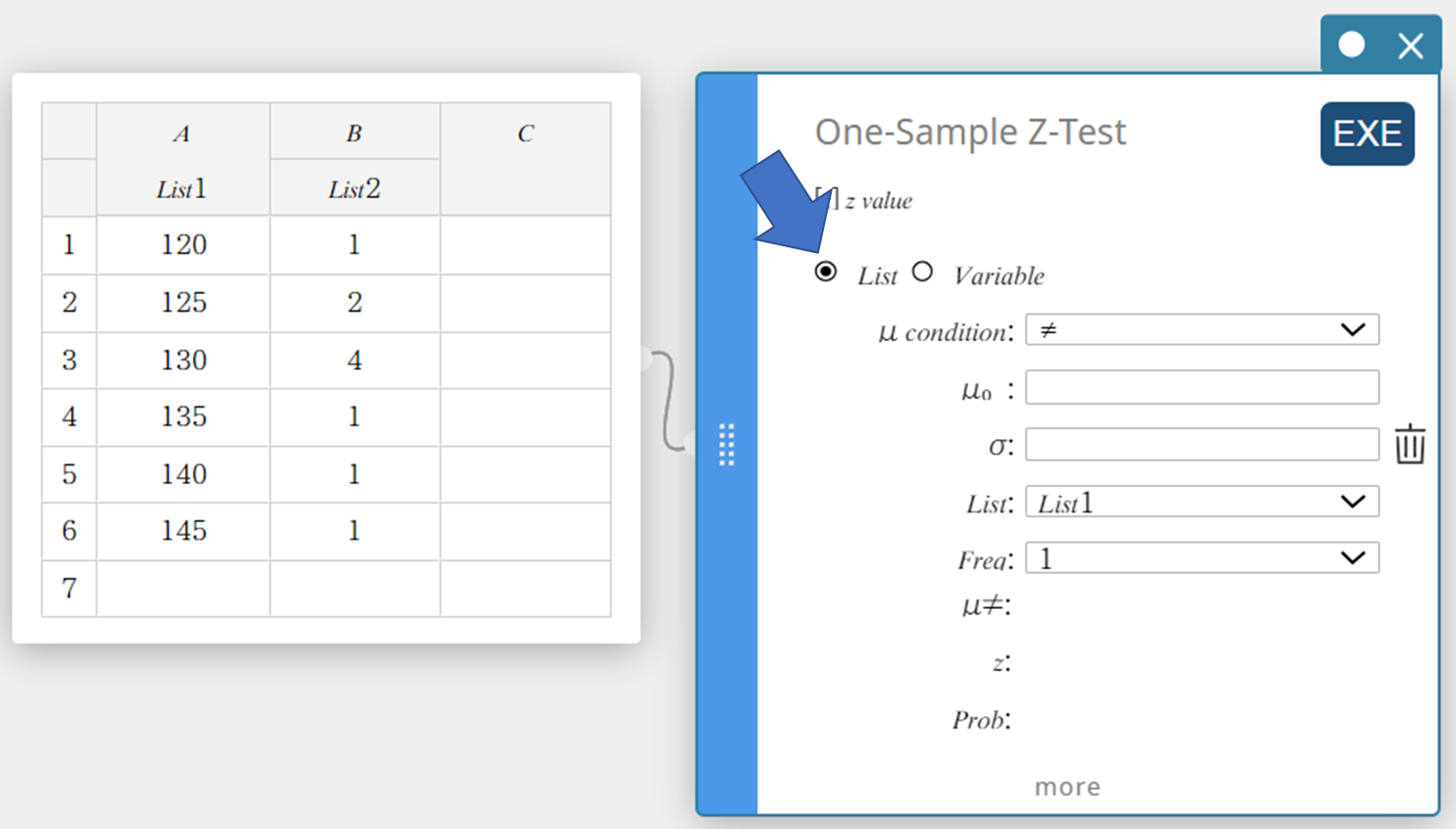
6. Defina as configurações conforme mostrado abaixo.
   \(\mu\) condição: No cardápio que aparece, selecione “\(\gt\)”.
   \(\mu_0\) : Entrada \(120\).
   \(\sigma\): Entrada \(19\).
   Lista: No cardápio que aparece, selecione “Lista1”.
   Frequência: No cardápio que aparece, selecione “Lista2”.
   
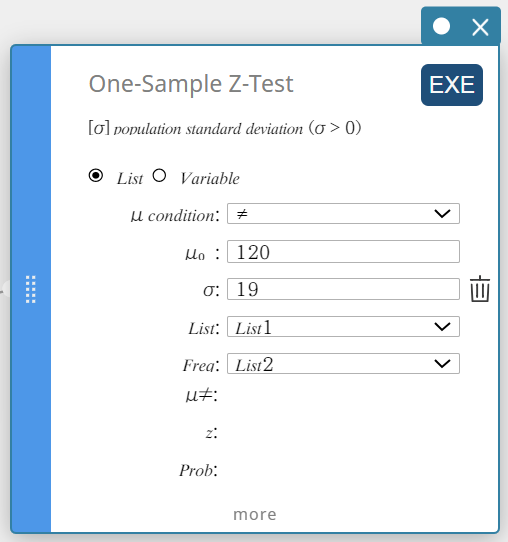
7. Clique [EXE].
   
   Isso exibe os resultados do cálculo e o gráfico.
   
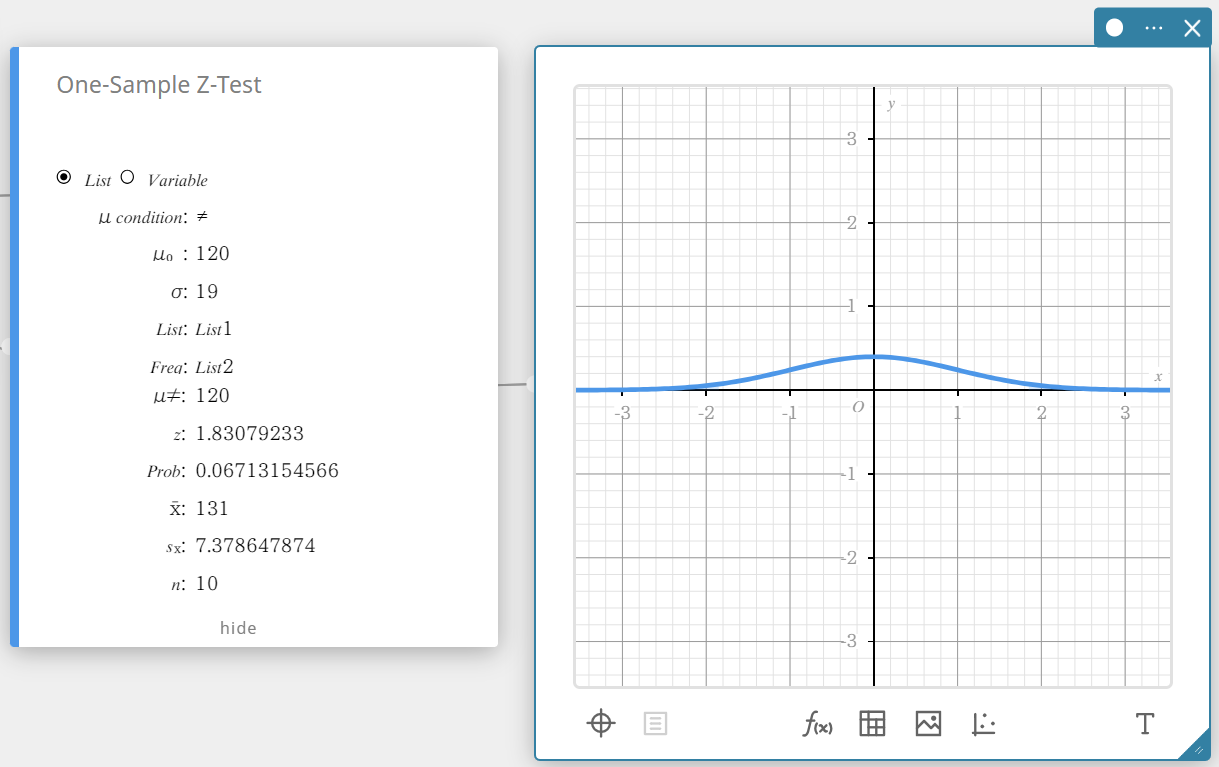
   \(\mu \gt\)　condição de valor médio da população
   \(\rm z\)　　　\(\rm z\) valor
   Problema　　\(\rm p\) valor
   \(\overline{x}\)　　　média da amostra
   \({\rm Sx}\)　　desvio padrão da amostra
   \(n\)　　　tamanho da amostra

Cálculos estatísticos e gráficos

Cálculos estatísticos

Uma variável
Isso exibe os resultados do cálculo de estatísticas de uma variável.

\(\bar{\rm x}\) … média da amostra
\(\Sigma {\rm x}\) … soma de dados
\(\Sigma {\rm x}^2\) … soma dos quadrados
\(\sigma {\rm x}\) … desvio padrão da população
\({\rm sx}\) … desvio padrão da amostra
\({\rm n}\) … tamanho da amostra
\({\rm min(x)}\) … mínimo
\({\rm Q}_1\) … primeiro quartil
\({\rm Med}\) … mediana
\({\rm Q}_3\) … terceiro quartil
\({\rm max(x)}\) … máximo
\({\rm Mode}\) … modo
\({\rm ModeN}\) … número de itens do modo de dados
\({\rm ModeF}\) … frequência do modo de dados

Quando \({\rm Mode}\) tem múltiplas soluções, todas elas são exibidas.

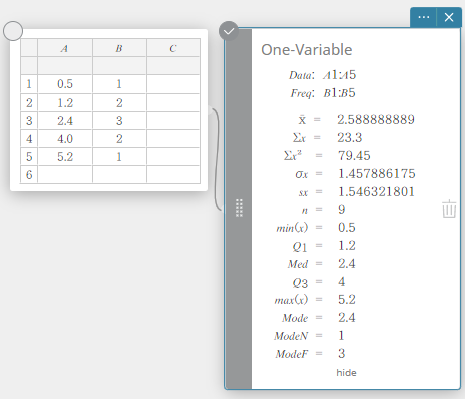
Duas Variáveis
Isso exibe os resultados do cálculo das estatísticas de variáveis binárias.

\(\bar{\rm x}\) … média da amostra
\(\Sigma {\rm x}\) … soma de dados
\(\Sigma {\rm x}^2\) … soma dos quadrados
\(\sigma {\rm x}\) … desvio padrão da população
\({\rm sx}\) … desvio padrão da amostra
\({\rm n}\) … tamanho da amostra
\(\bar{\rm y}\) … média da amostra
\(\Sigma {\rm y}\) … soma de dados
\(\Sigma {\rm y}^2\) … soma dos quadrados
\(\sigma {\rm y}\) … desvio padrão da população
\({\rm sy}\) … desvio padrão da amostra
\(\Sigma {\rm xy}\) … soma dos dados dos produtos Lista XL e Lista Y
\({\rm minX}\) … mínimo
\({\rm maxX}\) … máximo
\({\rm minY}\)… mínimo
\({\rm maxY}\) … máximo

Cálculos e gráficos de regressão

Regressão linear
A regressão linear usa o método dos mínimos quadrados para determinar a equação que melhor se ajusta aos seus pontos de dados e retorna valores para a inclinação e a interceptação em y. A representação gráfica desta relação é um gráfico de regressão linear.

\(y = a \cdot x + b\)
\(a\) … coeficiente de regressão (inclinação)
\(b\) … termo constante de regressão (interceptação y)
\(r\) … coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

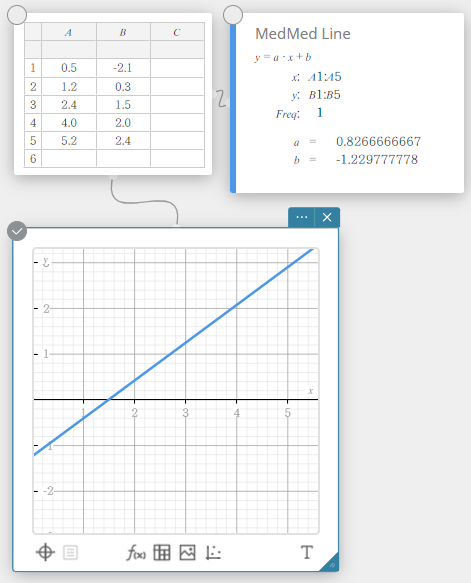
Regressão Med-Med
Quando você suspeita que os dados contêm valores extremos, você deve usar o gráfico Med-Med (que é baseado em medianas) no lugar do gráfico de regressão linear. O gráfico Med-Med é semelhante ao gráfico de regressão linear, mas também minimiza os efeitos de valores extremos.

\(y = a \cdot x + b\)
\(a\) … coeficiente de regressão (inclinação)
\(b\) … termo constante de regressão (interceptação y)

Regressão Quadrática
O gráfico de regressão quadrática usa o método dos mínimos quadrados para desenhar uma curva que passa pela vizinhança de tantos pontos de dados quanto possível. Este gráfico pode ser expresso como uma expressão de regressão quadrática.

\(y = a \cdot x^2 + b \cdot x + c\)
\(a\) … segundo coeficiente de regressão
\(b\) … primeiro coeficiente de regressão
\(c\) … termo constante de regressão (interceptação y)
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … coeficiente de determinação

Regressão Cúbica
O gráfico de regressão cúbica usa o método dos mínimos quadrados para desenhar uma curva que passa pela vizinhança de tantos pontos de dados quanto possível. Este gráfico pode ser expresso como uma expressão de regressão cúbica.

\(y = a \cdot x^3 + b \cdot x^2 + c \cdot x + d\)
\(a\) … terceiro coeficiente de regressão
\(b\) … segundo coeficiente de regressão
\(c\) … primeiro coeficiente de regressão
\(d\) … termo constante de regressão (interceptação y)
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

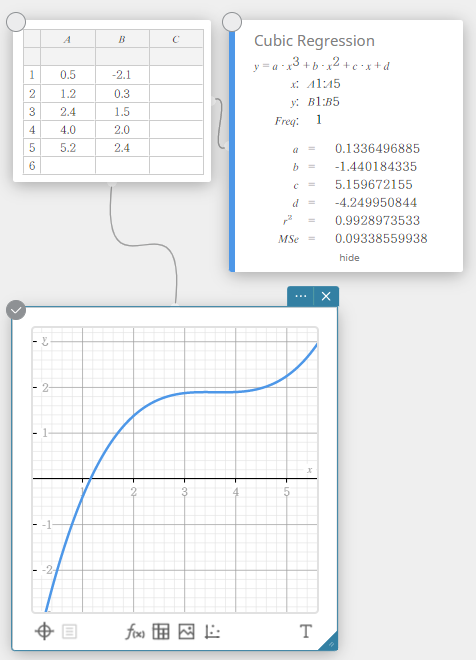
Regressão quártica
O gráfico de regressão quártica usa o método dos mínimos quadrados para desenhar uma curva que passa pela vizinhança de tantos pontos de dados quanto possível. Este gráfico pode ser expresso como uma expressão de regressão quártica.

\(y = a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e\)
\(a\) … quarto coeficiente de regressão
\(b\) … terceiro coeficiente de regressão
\(c\) … segundo coeficiente de regressão
\(d\) … primeiro coeficiente de regressão
\(e\) … termo constante de regressão (interceptação y)
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

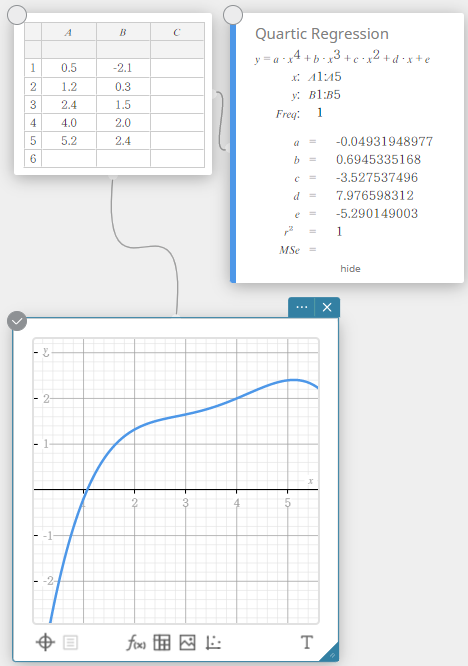
Regressão Logarítmica
A regressão logarítmica expressa \(y\) como uma função logarítmica de \(x\). A fórmula de regressão logarítmica normal é \(y=a+b \cdot \ln(x)\). Se dissermos isso \(X=\ln(x)\), então esta fórmula corresponde à fórmula de regressão linear \(y=a+b \cdot X\).

\(y = a + b \cdot \ln(x)\)
\(a\) … termo constante de regressão
\(b\) … Coeficiente de regressão
\(r\) … coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

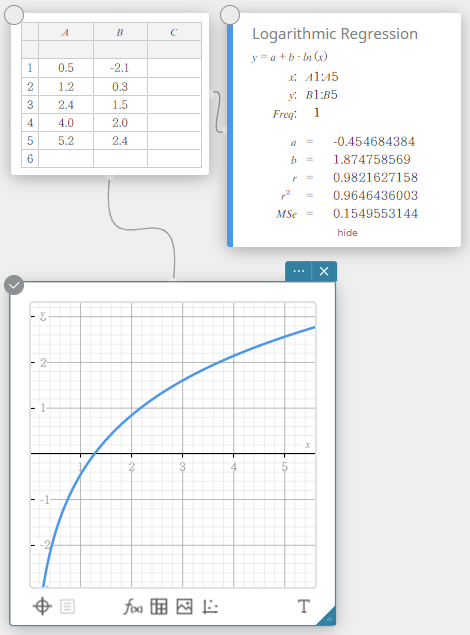
Regressão Exponencial
A regressão exponencial pode ser usada quando \(y\) é proporcional à função exponencial de \(x\). A fórmula de regressão exponencial normal é \(y=a \cdot e^{b \cdot x}\). Se obtivermos os logaritmos de ambos os lados, obtemos \(\ln(y)=\ln(a)+b \cdot x\). A seguir, se dissermos que \(Y=\ln(y)\) e \(A=\ln(a)\), a fórmula corresponde à fórmula de regressão linear \(Y=A+b \cdot x\).

\(y = a \cdot e^{b \cdot x}\)
\(a\) … Coeficiente de regressão
\(b\) … termo constante de regressão
\(r\) … coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

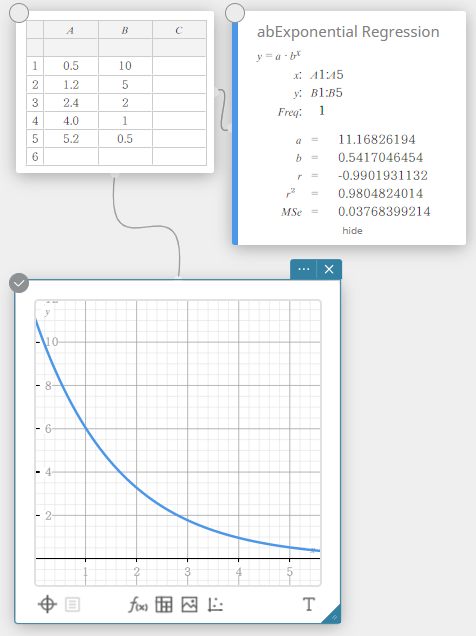
abRegressão Exponencial
A regressão exponencial pode ser usada quando \(y\) é proporcional à função exponencial de \(x\). A fórmula de regressão exponencial normal neste caso é \(y=a \cdot b^x\). Se tomarmos os logaritmos naturais de ambos os lados, obtemos \(\ln(y)=\ln(a)+(\ln(b)) \cdot x\). A seguir, se dissermos que \(Y=\ln(y)\), \(A=\ln(a)\) e \(B=\ln(b)\), a fórmula corresponde à fórmula de regressão linear \(Y=A+B \cdot x\).

\(y = a \cdot b^x\)
\(a\) … termo constante de regressão
\(b\) … Coeficiente de regressão
\(r\) … coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

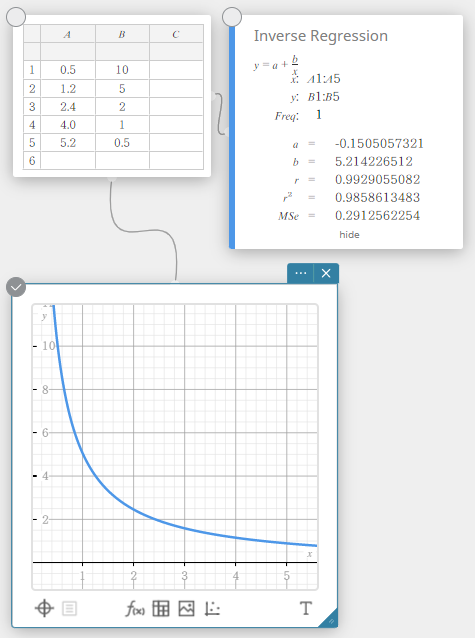
Regressão Inversa
A regressão inversa expressa \(y\) como uma função inversa de \(x\). A fórmula de regressão inversa normal é \(y=a+b/x\). Se dissermos isso \(X=1/x\), então esta fórmula corresponde à fórmula de regressão linear \(y=a+b･X\).

\(y=a+b/x\)
\(a\) … termo constante de regressão
\(b\) … Coeficiente de regressão
\(r\) …. coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

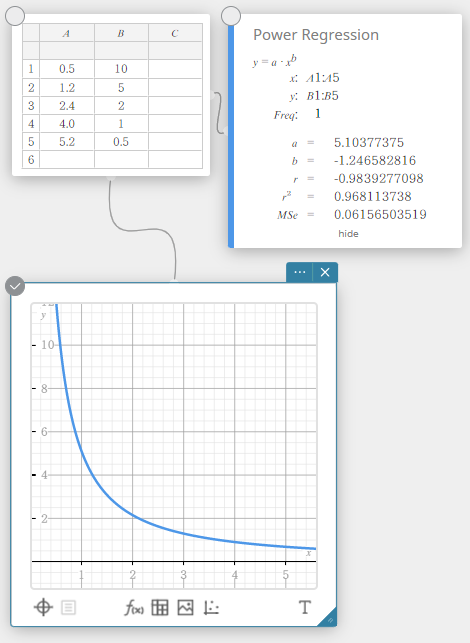
Regressão de potência
A regressão de potência pode ser usada quando \(y\) é proporcional à potência de \(x\). A fórmula normal de regressão de potência é \(y=a \cdot x^b\). Se obtivermos os logaritmos naturais de ambos os lados, obtemos \(\ln(y)=\ln(a)+b \cdot \ln(x)\). A seguir, se dissermos que \(X=\ln(x)\), \(Y=\ln(y)\), e \(A=\ln(a)\), a fórmula corresponde à fórmula de regressão linear \(Y=A+b \cdot X\).

\(y = a \cdot x^b\)
\(a\) … Coeficiente de regressão
\(b\) … poder de regressão
\(r\) … coeficiente de correlação
\(r^2\) … coeficiente de determinação
\({\rm MSe}\) … erro quadrático médio

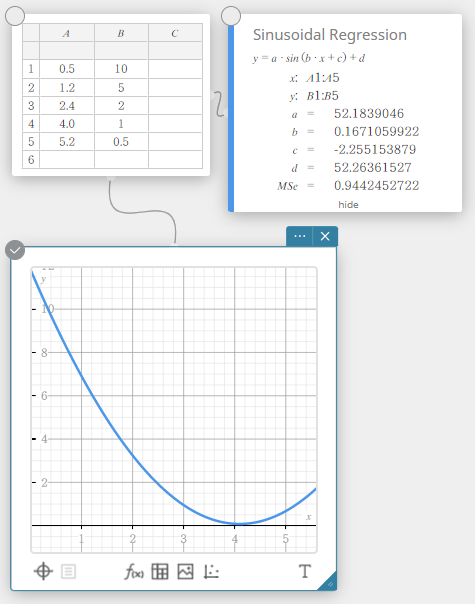
Regressão sinusoidal
A regressão sinusoidal é melhor para dados que se repetem em um intervalo fixo regular ao longo do tempo.

\(y = a \cdot \sin( b \cdot x + c ) + d\)
\(a\), \(b\), \(c\), \(d\) … Coeficiente de regressão
\({\rm MSe}\) … erro quadrático médio

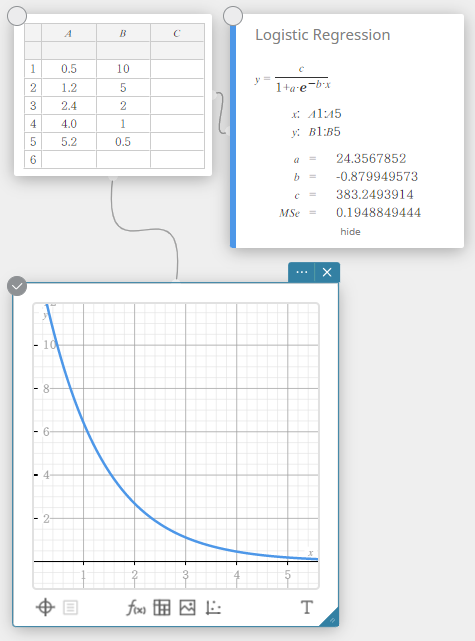
Regressão Logística
A regressão logística é melhor para dados cujos valores aumentam continuamente ao longo do tempo, até atingir um ponto de saturação.

\(\displaystyle y=\frac{c}{1+a \cdot e^{-b \cdot x}}\)
\(a\), \(b\), \(c\) … Coeficiente de regressão
\({\rm MSe}\) … erro quadrático médio

Testes

Teste Z de uma amostra
Testa uma média amostral única em relação à média conhecida da hipótese nula quando o desvio padrão da população é conhecido. A distribuição normal é usada para o teste Z de uma amostra.

\(Z=\displaystyle \frac{\overline{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) : média da amostra
\(\mu_{0}\) : média populacional presumida
\(\sigma\) : desvio padrão da população
\(n\) : tamanho da amostra

Tipo de dados: Variável

• Termos de entrada
  \( \mu \) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  \( \mu_{0} \) : média populacional presumida
  \( \sigma \) : desvio padrão da população（\( \sigma > 0 \)）
  \(\overline{x}\) : média da amostra
  \(n\) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  \( \mu \neq \) : condição de valor médio da população
  \(z\) : valor z
  Problema : \(p\) valor

Tipo de dados: Lista

• Termos de entrada
  \( \mu \) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  \( \mu_{0} \) : média populacional presumida
  \( \sigma \) : desvio padrão da população （\( \sigma > 0 \)）
  Lista : lista de dados
  Frequencia : frequência (1 ou nome da lista)

• Termos de saída
  \( \mu \neq \) : condição de valor médio da população
  \(z\) : \(z\) valor
  Problema : \(p\) valor
  \( \overline{x} \) : média da amostra
  \( s_{x} \) : desvio padrão da amostra
  \( n \) : tamanho da amostra

Teste Z de duas amostras
Testa a diferença entre duas médias quando os desvios padrão das duas populações são conhecidos. A distribuição normal é usada para o teste Z de duas amostras.

\( Z=\displaystyle \frac{ \overline{x}_{1} – \overline{x}_{2} }{ \sqrt{\displaystyle \frac{{\sigma_{1}}^2}{n_{1}} +\displaystyle \frac{{\sigma_{2}}^2}{n_{2}} } } \)

\( \overline{x}_{1} \) : média amostral dos dados da amostra 1
\( \overline{x}_{2} \) : média amostral dos dados da amostra 2
\( \sigma_{1} \) : desvio padrão populacional da amostra 1
\( \sigma_{2} \) : desvio padrão populacional da amostra 2
\( n_{1} \) : tamanho da amostra 1
\( n_{2} \) : tamanho da amostra 2

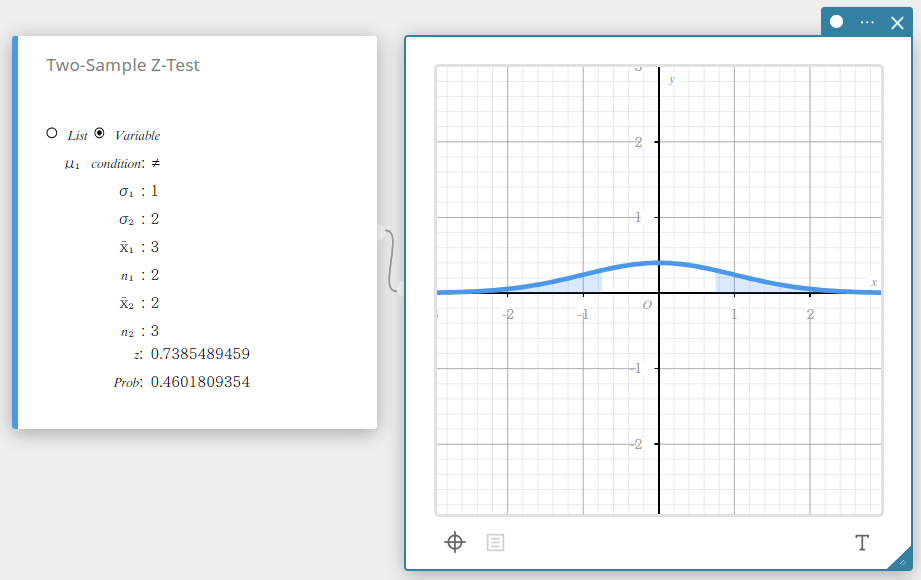
Tipo de dados: Variável

• Termos de entrada
  \( \mu_{1} \) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2).
  \( \sigma_{1} \) : desvio padrão populacional da amostra 1 （\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : desvio padrão populacional da amostra 2（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( n_{1} \) : tamanho da amostra 1 (número inteiro positivo)
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( n_{2} \) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  \(z\) : valor z
  Problema : \(p\) valor

Tipo de dados: Lista

• Termos de entrada
  \( \mu_{1} \) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2).
  \( \sigma_{1} \) : desvio padrão populacional da amostra 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : desvio padrão populacional da amostra 2（\( \sigma_{2} > 0 \)）
  Lista(1): lista onde os dados da amostra 1 estão localizados
  Lista(2): lista onde os dados da amostra 2 estão localizados
  Frequência(1): frequência da amostra 1 (1 ou nome da lista)
  Frequência(2): frequência da amostra 2 (1 ou nome da lista)

• Termos de saída
  \(z\) : valor z
  Problema : \(p\) valor
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( s_{x_{1}} \) : desvio padrão amostral da amostra 1
  \( s_{x_{2}} \) : desvio padrão amostral da amostra 2
  \( n_{1} \) : tamanho da amostra 1
  \( n_{2} \) : tamanho da amostra 2

Teste Z de uma proporção (Teste Z de uma proporção)
Testa uma única proporção de amostra em relação à proporção conhecida da hipótese nula. A distribuição normal é usada para o Teste Z de Uma Proporção.

\(Z =\displaystyle \frac{\displaystyle \frac{x}{n} – p_{0} }{ \sqrt{\displaystyle \frac{ p_{0}(1-p_{0}) }{n} }}\)
\(p_{0}\) : proporção esperada da amostra
\(n\) : tamanho da amostra

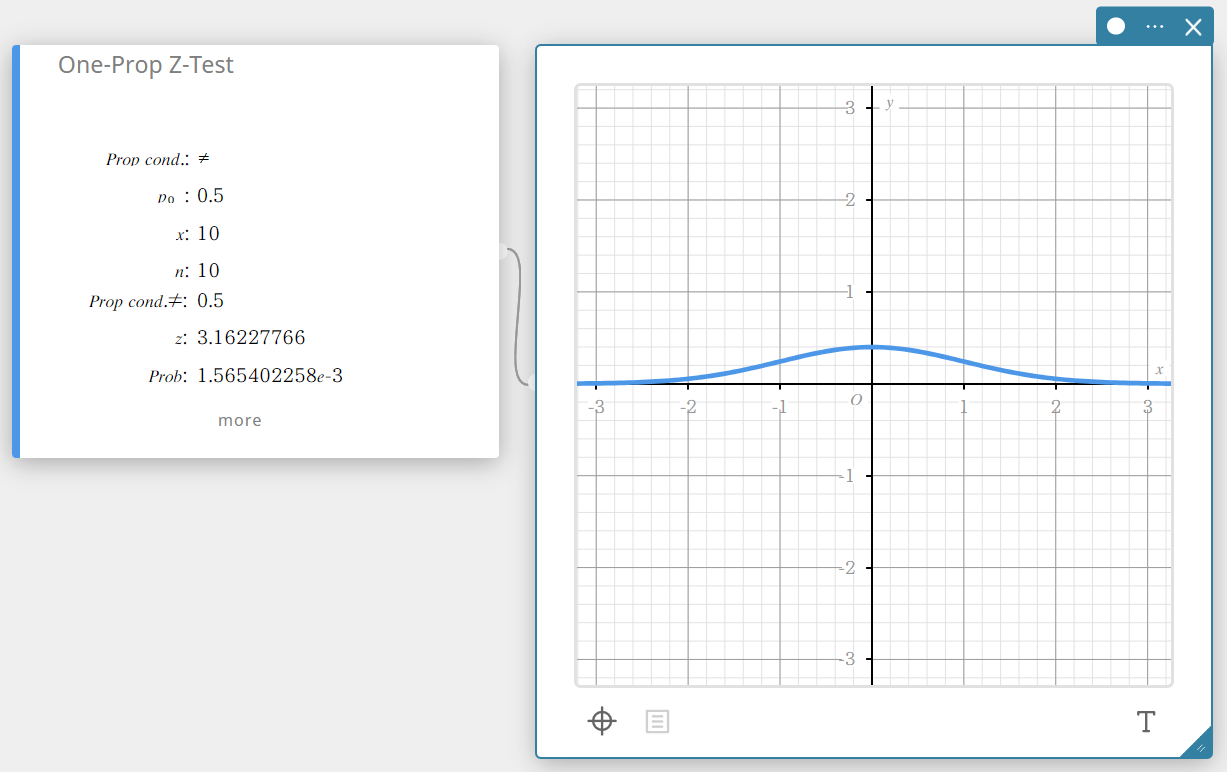
• Termos de entrada
  Condição da hélice : condição de teste de proporção de amostra (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  \(p_{0}\) : proporção esperada da amostra（\( 0 < p_{0} < 1 \)）
  \(x\) : valor da amostra (inteiro, \( x \geq 0 \)）
  \(n\) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  Condição de hélice \(\neq\) : condição de teste de proporção de amostra
  \(z\) : valor z
  Problema : \(p\) valor
  \(\hat{p}\) : proporção amostral estimada

Teste Z de duas proporções (Teste Z de duas proporções)
Testa a diferença entre duas proporções de amostra. A distribuição normal é usada para o Teste Z de Duas Proporções.

\( Z =\displaystyle \frac{\displaystyle \frac{x_{1}}{n_{1}} -\displaystyle \frac{x_{2}}{n_{2}} }{ \sqrt{ \hat{p} \left(1-\hat{p} \right) \left(\displaystyle \frac{1}{n_{1}} +\displaystyle \frac{1}{n_{2}} \right) } }\)
\(x_{1}\) : valor dos dados da amostra 1
\(x_{2}\) : valor dos dados da amostra 2
\(n_{1}\) : tamanho da amostra 1
\(n_{2}\) : tamanho da amostra 2
\(\hat{p}\) : proporção amostral estimada

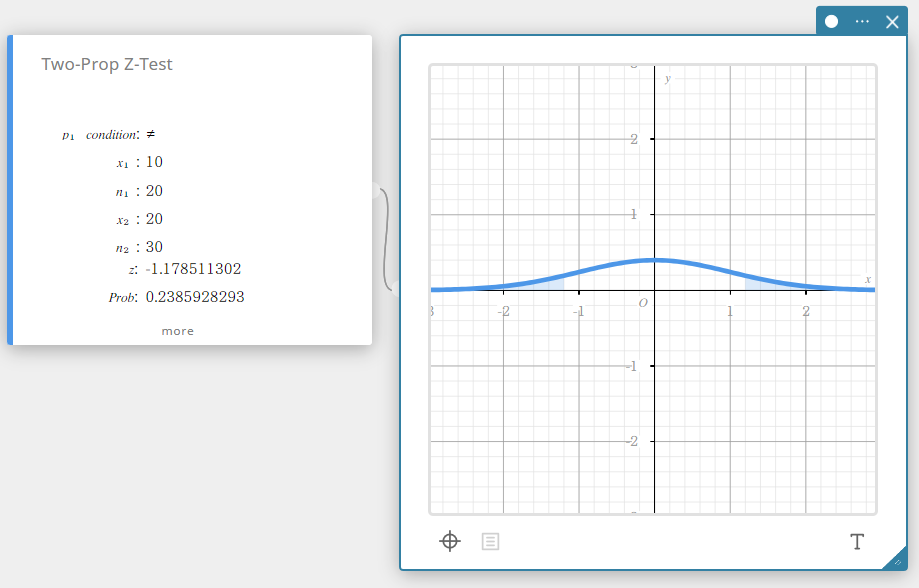
• Termos de entrada
  \(p_{1}\) condição: condições de teste de proporção de amostra (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2.)
  \(x_{1}\) : valor dos dados da amostra 1 (inteiro, \(x_{1}\) deve ser menor ou igual a \(n_{1}\))
  \(n_{1}\) : tamanho da amostra 1 (número inteiro positivo)
  \(x_{2}\) : valor dos dados da amostra 2 (inteiro, \(x_{2}\) deve ser menor ou igual a \(n_{2}\))
  \(n_{2}\) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  \(z\) : valor z
  Problema : \(p\) valor
  \(\hat{p}_{1}\) : proporção estimada da amostra 1
  \(\hat{p}_{2}\) : proporção estimada da amostra 2
  \(\hat{p}\) : proporção amostral estimada

Uma amostra \(t\) -Teste
Testa uma média amostral única em relação à média conhecida da hipótese nula quando o desvio padrão da população é desconhecido. A distribuição \(t\) é usada para o teste \(t\) de uma amostra.

\(t =\displaystyle \frac{ \overline{x} – \mu_{0} }{\displaystyle \frac{ s_{x} }{ \sqrt{n} } }\)
\(\overline{x}\) : média da amostra
\(\mu_{0}\) : média populacional presumida
\(s_{x}\) : desvio padrão da amostra
\(n\) : tamanho da amostra

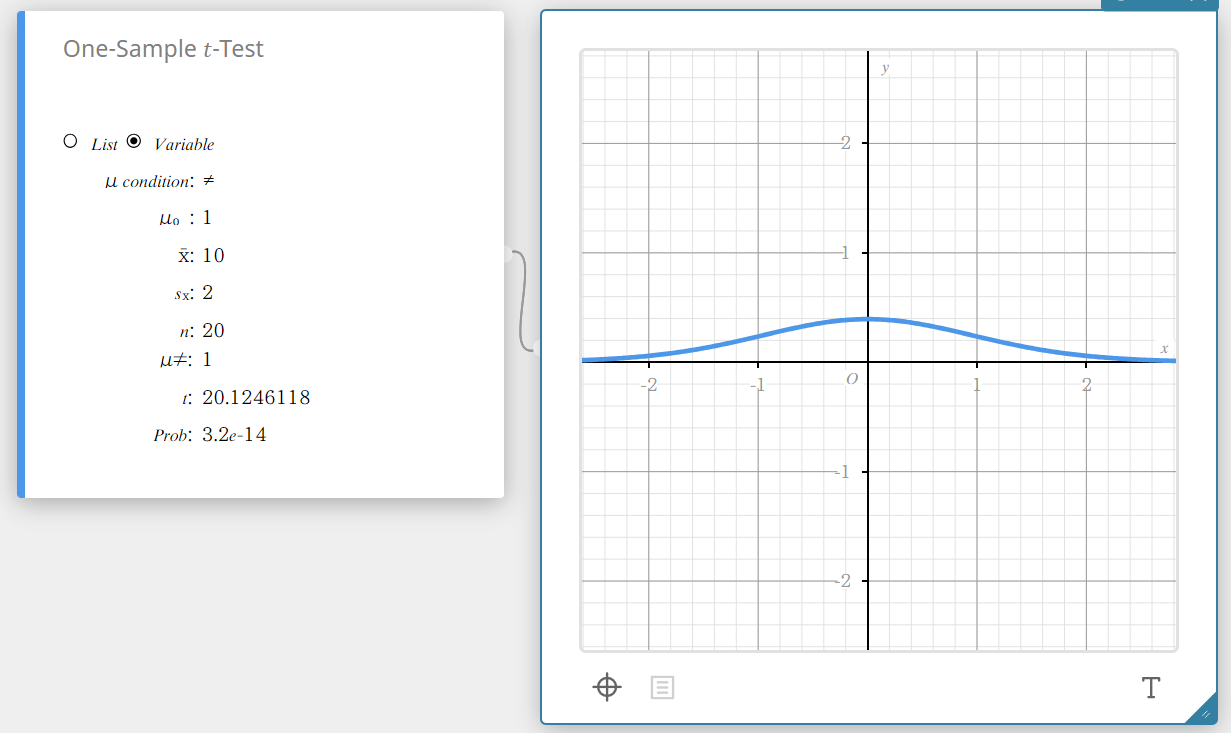
Tipo de dados: Variável

• Termos de entrada
  \(\mu\) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  \(\mu_{0}\) : média populacional presumida
  \(\overline{x}\) : média da amostra
  \(s_{x}\) : desvio padrão da amostra（\( s_{x} > 0 \)）
  \(n\) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  \(\mu \ne\) : condições de teste do valor médio da população
  \(t\) : \(t\) valor
  Problema : \(p\) valor

Tipo de dados: Lista

• Termos de entrada
  \(\mu\) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  \(\mu_{0}\) : média populacional presumida
  Lista : lista de dados
  Frequencia : frequência (1 ou nome da lista)

• Termos de saída
  \(\mu \ne\) : condições de teste do valor médio da população
  \(t\) : \(t\) valor
  Problema : \(p\) valor
  \(\overline{x}\) : média da amostra
  \(s_{x}\) : desvio padrão da amostra
  \(n\) : tamanho da amostra

Teste \(t\) de duas amostras
Testa a diferença entre duas médias quando os desvios padrão das duas populações são desconhecidos. A distribuição \(t\) é usada para o teste \(t\) de duas amostras.

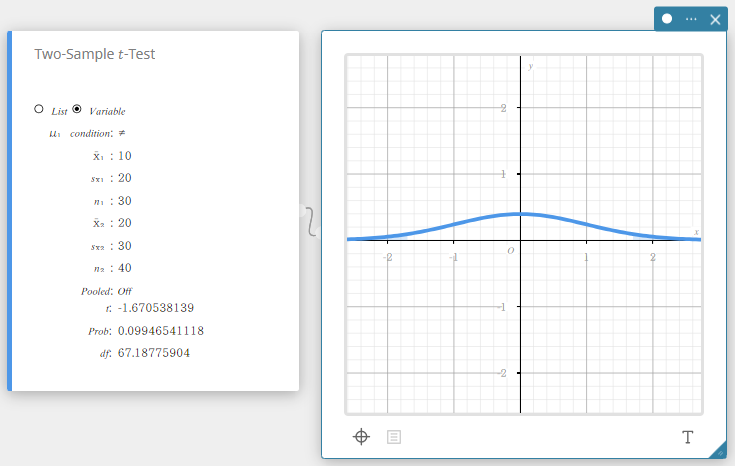
• Quando os dois desvios padrão populacionais são iguais (agrupados)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{{s_{p}}^2 \left(\displaystyle \frac{1}{n_1} + \displaystyle \frac{1}{n_2} \right)}}\)
  \(df=n_1+n_2-2\)
  \(s_p=\sqrt{ \displaystyle \frac{(n_1-1){s_{x_1}}^2 + (n_2-1){s_{x_2}}^2}{n_1+n_2-2} }\)

• Quando os dois desvios padrão da população não são iguais (não agrupados)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{\displaystyle \frac{{s_{x_1}}^2}{n_1} + \displaystyle \frac{{s_{x_2}}^2}{n_2}}}\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{(1-C)^2}{n_2-1}}\)
  \(C =\displaystyle \frac{\displaystyle \frac{{s_{x_1}}^2}{n_1}}{\displaystyle \frac{{s_{x_1}}^2}{n_1} +\displaystyle \frac{{s_{x_2}}^2}{n_2}}\)

\(x_1\): média amostral dos dados da amostra 1
\(x_2\): média amostral dos dados da amostra 2
\(s_{x_1}\) : desvio padrão amostral da amostra 1
\(s_{x_2}\) : desvio padrão amostral da amostra 2
\(s_p\) : desvio padrão da amostra agrupada
\(n_1\) : tamanho da amostra 1
\(n_2\) : tamanho da amostra 2

Tipo de dados: Variável

• Termos de entrada
  \(\mu_1\) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2.)
  \(\overline{x}_1\) : média amostral dos dados da amostra 1
  \(s_{x_1}\) : desvio padrão amostral da amostra 1（\(s_{x_1} > 0\)）
  \(n_1\) : tamanho da amostra 1 (número inteiro positivo)
  \(\overline{x}_2\) : média amostral dos dados da amostra 2
  \(s_{x_2}\) : desvio padrão amostral da amostra 2（\(s_{x_2} > 0\)）
  \(n_2\) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  \(t\) : \(t\) valor
  Problema : \(p\) valor
  \(df\) : graus de liberdade
  \(s_p\) : desvio padrão da amostra agrupada

Tipo de dados: Lista

• Termos de entrada
  \(\mu_1\) condição: condições de teste do valor médio da população (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2.)
  Lista(1) : lista onde os dados da amostra 1 estão localizados
  Lista(2) : lista onde os dados da amostra 2 estão localizados
  Frequência(1) : frequência da amostra 1 (1 ou nome da lista)
  Frequência(2) : frequência da amostra 2 (1 ou nome da lista)
  Agrupados : Ativado (variâncias iguais) ou Desativado (variâncias desiguais)

• Termos de saída
  \(t\) : \(t\) valor
  Problema : \(p\) valor
  \(df\) : graus de liberdade
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( s_{x_{1}} \) : desvio padrão amostral da amostra 1
  \( s_{x_{2}} \) : desvio padrão amostral da amostra 2
  \(s_p\) : desvio padrão da amostra agrupada
  \( n_{1} \) : tamanho da amostra 1
  \( n_{2} \) : tamanho da amostra 2

Registro Linear \(t\) -Teste (Regressão Linear \(t\) -Teste)
Testa a relação linear entre as variáveis emparelhadas ( x , y ). O método dos mínimos quadrados é usado para determinar aeb, que são os coeficientes da fórmula de regressão \(y = a + b \cdot x\). O valor p é a probabilidade da inclinação da regressão da amostra ( b ) desde que a hipótese nula seja verdadeira, \(\beta = 0\). A distribuição t é usada para o teste de regressão linear \(t\).

\(t=r\sqrt{\displaystyle \frac{n-2}{1-r^2}}\)
\( \displaystyle b=\left\{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) \right\} / \left\{\sum_{i=1}^n (x_i-\overline{x})^2 \right\}\)
\(a=\overline{y}-b\overline{x}\)

\(a\) : termo constante de regressão (interceptação y)
\(b\) : coeficiente de regressão (inclinação)
\(n\) : tamanho da amostra（\(n \ge 3\)）
\(r\) : coeficiente de correlação
\(r^2\) : coeficiente de determinação

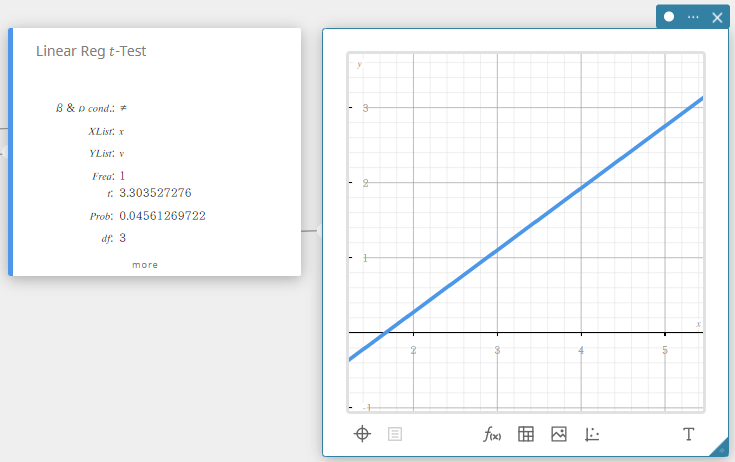
• Termos de entrada
  \(\beta\ \&\ \rho\) condição: condições de teste (“\(\neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal inferior, “>” especifica o teste unicaudal superior.)
  Lista XL : x -lista de dados
  Lista Y : y -lista de dados
  Frequencia : frequência (1 ou nome da lista)

• Termos de saída
  \(t\) : \(t\) valor
  Problema : \(p\) valor
  \(df\) : graus de liberdade
  \(a\) : termo constante de regressão (interceptação y)
  \(b\) : coeficiente de regressão (inclinação)
  se : erro padrão de estimativa sobre a linha de regressão de mínimos quadrados
  \(r\) : coeficiente de correlação
  \(r^2\) : coeficiente de determinação
  SEb: erro padrão da inclinação dos mínimos quadrados

\(\chi^2\) Teste
Testa a independência de duas variáveis categóricas dispostas em forma de matriz. O teste de independência \(\chi^2\) compara a matriz observada com a matriz teórica esperada. A distribuição \(\chi^2\) é usada para o teste \(\chi^2\).

MEMORANDO
O tamanho mínimo da matriz é 1×2. Ocorre um erro se a matriz tiver apenas uma coluna.
O resultado do cálculo da frequência esperada é armazenado na variável de sistema denominada “Esperado”.

\( \chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{l} \displaystyle \frac{(x_{ij}-F_{ij})^2}{F_{ij}} \)
\( F_{ij}=\frac{{\displaystyle\sum_{i=1}^k}x_{ij}\times{\displaystyle\sum_{j=1}^lx_{ij}}}{{\displaystyle\sum_{i=1}^k}{\displaystyle\sum_{j=1}^l}x_{ij}} \)
\( x_{ij}\) : O elemento na linha i, coluna j da matriz observada
\( F_{ij}\) : O elemento na linha i, coluna j da matriz esperada

• Termos de entrada
  Matriz: nome da matriz contendo valores observados (números inteiros positivos em todas as células para matrizes 2×2 e maiores; números reais positivos para matrizes de uma linha)

• Termos de saída
  \(\chi^2\) : \(\chi^2\) valor
  Problema : \(p\) valor
  \(df\) : graus de liberdade
  Observado: a matriz de entrada dos valores observados
  Esperado: a matriz calculada de valores esperados

\(\chi^2\) Teste GOF (\(\chi^2\) Teste de qualidade de ajuste)
Testa se a contagem observada de dados amostrais se ajusta a uma determinada distribuição. Por exemplo, pode ser usado para determinar a conformidade com distribuição normal ou distribuição binomial.


\(\chi^2=\sum_i^k \displaystyle \frac{ (O_i – E_i )^2 }{E_i}\)
\(Contrib = \left\{\displaystyle \frac{ (O_1 – E_1 )^2 }{E_1} \ \displaystyle \frac{ (O_2 – E_2 )^2 }{E_2} \cdots \displaystyle \frac{ (O_k – E_k )^2 }{E_k} \right\} \)

\(O_i\) : O i-ésimo elemento da lista observada
\(E_i\) : O i-ésimo elemento da lista esperada

• Termos de entrada
  Lista observada: nome da lista contendo contagens observadas (todas as células são números inteiros positivos)
  Lista esperada: nome da lista que serve para salvar a frequência esperada
  \(df\) : graus de liberdade

• Termos de saída
  \(\chi^2\) : \(\chi^2\) valor
  Problema : \(p\) valor
  \(df\) : graus de liberdade
  Contrib: nome da lista especificando a contribuição de cada contagem observada

Teste F de duas amostras
Testa a razão entre as variâncias amostrais de duas amostras aleatórias independentes. A distribuição F é usada para o teste F de duas amostras.

\( F=\displaystyle \frac{{S_{x_1}}^2}{{S_{x_2}}^2}\)

Tipo de dados: Variável

• Termos de entrada
  \( \sigma_1\) condição: condições de teste de desvio padrão da população (“\( \neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2.)
  \( s_{x_1}\) : desvio padrão amostral da amostra 1（ \( s_{x_1} > 0\)）
  \( n_1\) : tamanho da amostra 1 (número inteiro positivo)
  \( s_{x_2}\) : desvio padrão amostral da amostra 2（ \( s_{x_2} > 0\)）
  \( n_2\) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  \( F\) : Valor F
  Problema: valor p

Tipo de dados: Lista

• Termos de entrada
  \( \sigma_1\) condição: condições de teste de desvio padrão da população (“\( \neq\)” especifica o teste bicaudal, “<” especifica o teste unicaudal onde a amostra 1 é menor que a amostra 2, “>” especifica o teste unicaudal onde a amostra 1 é maior que a amostra 2.)
  Lista(1) : lista onde os dados da amostra 1 estão localizados
  Lista(2) : lista onde os dados da amostra 2 estão localizados
  Frequência(1) : frequência da amostra 1 (1 ou nome da lista)
  Frequência(2) : frequência da amostra 2 (1 ou nome da lista)

• Termos de saída
  \( F\) : Valor F
  Problema: valor p
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( s_{x_{1}} \) : desvio padrão amostral da amostra 1
  \( s_{x_{2}} \) : desvio padrão amostral da amostra 2
  \( n_{1} \) : tamanho da amostra 1
  \( n_{2} \) : tamanho da amostra 2

ANOVA unidirecional (análise de variância unidirecional)
Testa a hipótese de que as médias populacionais de múltiplas populações são iguais. Compara a média de um ou mais grupos com base em uma variável ou fator independente.

• Termos de entrada
  Lista de Fatores(A) : lista onde os níveis do Fator A estão localizados
  DependentList: lista onde os dados de amostra estão localizados

• Termos de saída
  A df : graus de liberdade do Fator A
  A MS : quadrado médio do Fator A
  A SS : soma dos quadrados do Fator A
  A F : valor F do Fator A
  A p : valor p do Fator A
  Err df : graus de liberdade de erro
  Err MS : quadrado médio do erro
  Err SS : soma dos quadrados do erro

ANOVA bidirecional (análise de variância bidirecional)
Testa a hipótese de que as médias populacionais de múltiplas populações são iguais. Ele examina o efeito de cada variável de forma independente, bem como sua interação entre si com base em uma variável dependente.

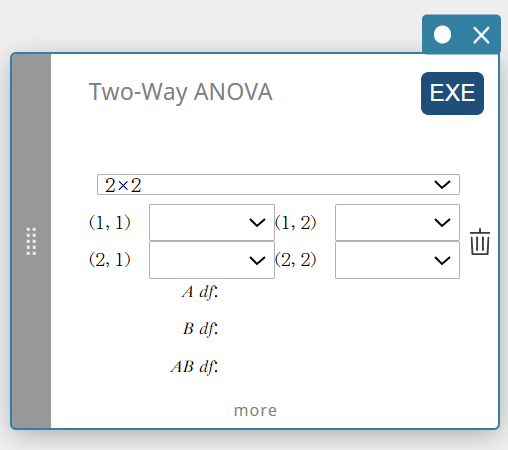
• Termos de entrada
  2×2: tipo de tabela de dados
  Lista de Fatores(A) : lista onde os níveis do Fator A estão localizados
  Lista de Fatores(B) : lista onde os níveis do Fator B estão localizados
  Lista Dependente : lista onde os dados de amostra estão localizados

• Termos de saída
  A df : graus de liberdade do Fator A
  A MS : quadrado médio do Fator A
  A SS : soma dos quadrados do Fator A
  A F : valor F do Fator A
  A p : valor p do Fator A
  B df : graus de liberdade do Fator B
  B MS : quadrado médio do Fator B
  B SS : soma dos quadrados do Fator B
  B F : valor F do Fator B
  B p : valor p do Fator B
  AB df : graus de liberdade do Fator A × Fator B
  AB MS : quadrado médio do Fator A × Fator B
  AB SS : soma dos quadrados do Fator A × Fator B
  AB F : valor F do Fator A × Fator B
  AB p : valor p do Fator A × Fator B
  Err df : graus de liberdade de erro
  Err MS : quadrado médio do erro
  Err SS : soma dos quadrados do erro

Intervalos de confiança

Intervalo Z de uma amostra
Calcula o intervalo de confiança para a média populacional com base em uma média amostral e um desvio padrão populacional conhecido.

\(Lower = \overline{x}-Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(Upper = \overline{x}+Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(\alpha\) é o nível de significância, e \(100(1 – \alpha)\%\) é o nível de confiança. Quando o nível de confiança é \(95\%\), por exemplo, você inseriria 0.95, que produz α = 1 – 0.95 = 0.05.

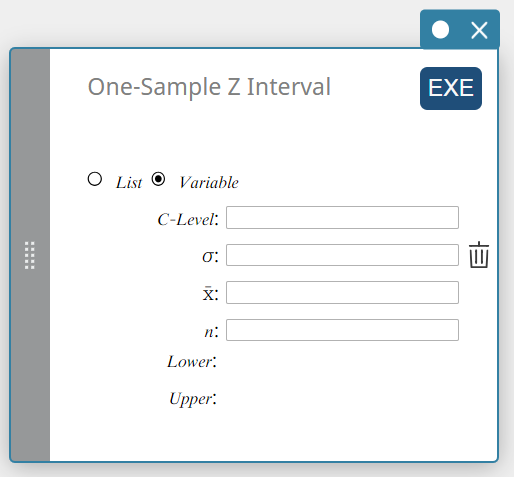
Tipo de dados: Variável

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \sigma \) : desvio padrão da população（\( \sigma > 0 \)）
  \( \overline{x} \) : média da amostra
  \( n \) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)

Tipo de dados: Lista

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \sigma \) : desvio padrão da população（\( \sigma > 0 \)）
  Lista: lista onde os dados de amostra estão localizados
  Frequencia : frequência da amostra (1 ou nome da lista)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \( \overline{x} \) : média da amostra
  \( s_{x} \) : desvio padrão da amostra
  \( n \) : tamanho da amostra

Intervalo Z de duas amostras
Calcula o intervalo de confiança para a diferença entre as médias populacionais com base na diferença entre as médias amostrais quando os desvios padrão da população são conhecidos.


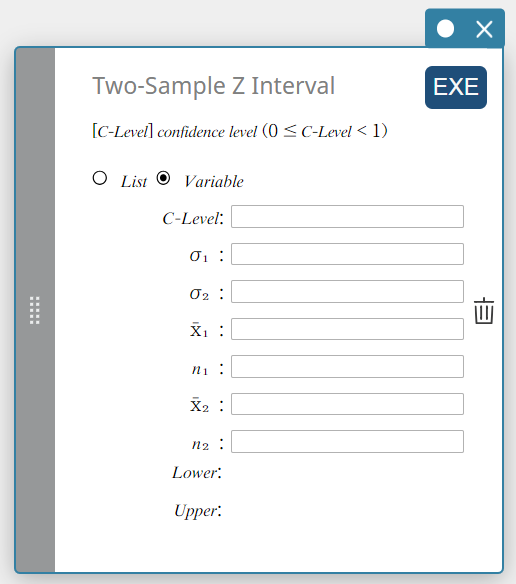
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)

Tipo de dados: Variável

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \sigma_{1} \) : desvio padrão populacional da amostra 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : desvio padrão populacional da amostra 2（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( n_{1} \) : tamanho da amostra 1 (número inteiro positivo)
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( n_{2} \) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)

Tipo de dados: Lista

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \sigma_{1} \) : desvio padrão populacional da amostra 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : desvio padrão populacional da amostra 2（\( \sigma_{2} > 0 \)）
  Lista(1) : lista onde os dados da amostra 1 estão localizados
  Lista(2) : lista onde os dados da amostra 2 estão localizados
  Frequência(1) : frequência da amostra 1 (1 ou nome da lista)
  Frequência(2) : frequência da amostra 2 (1 ou nome da lista)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( s_{x_{1}} \) : desvio padrão amostral da amostra 1
  \( s_{x_{2}} \) : desvio padrão amostral da amostra 2
  \( n_{1} \) : tamanho da amostra 1
  \( n_{2} \) : tamanho da amostra 2

Intervalo Z de uma proporção (intervalo Z de uma proporção)
Calcula o intervalo de confiança para a proporção da população com base em uma proporção de amostra única.


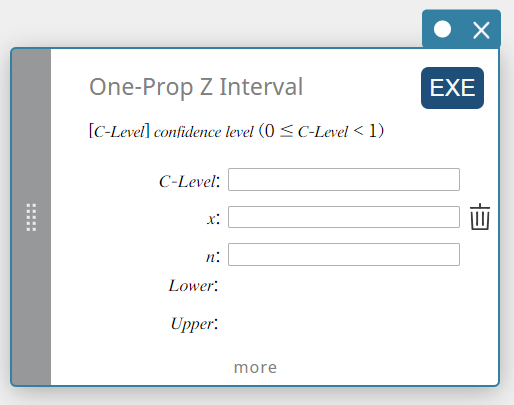
\(Lower =\displaystyle \frac{x}{n}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
\(Upper =\displaystyle \frac{x}{n}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( x \) : dados (0 ou número inteiro positivo)
  \( n \) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \(\hat{p}\) : proporção amostral estimada

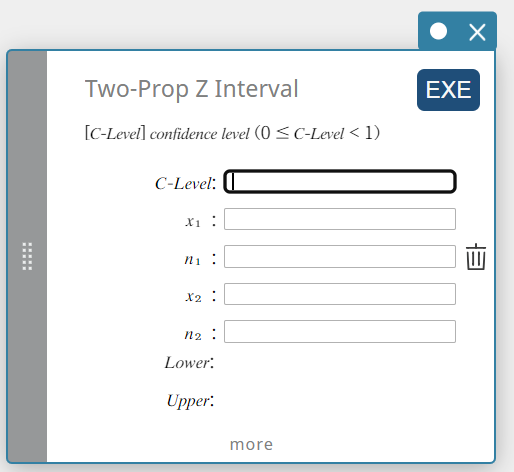
Intervalo Z de duas proporções (intervalo Z de duas proporções)
Calcula o intervalo de confiança para a diferença entre as proporções populacionais com base na diferença entre o intervalo Z de duas proporções.


\( Lower =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1- \displaystyle\frac{x_1}{n_1} \right) }{n_1} + \displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1- \displaystyle \frac{x_2}{n_2} \right) }{n_2} } \)
\( Upper =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1-\displaystyle \frac{x_1}{n_1} \right) }{n_1} +\displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1-\displaystyle\frac{x_2}{n_2} \right) }{n_2} } \)

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \(x_{1}\) : valor dos dados da amostra 1 (inteiro, \(x_{1}\) deve ser menor ou igual a \(n_{1}\))
  \(n_{1}\) : tamanho da amostra 1 (número inteiro positivo)
  \(x_{2}\) : valor de dados da amostra 2 (inteiro, \(x_{2}\) deve ser menor ou igual a \(n_{2}\))
  \(n_{2}\) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \(\hat{p}_{1}\) : proporção estimada da amostra 1
  \(\hat{p}_{2}\) : proporção estimada da amostra 2

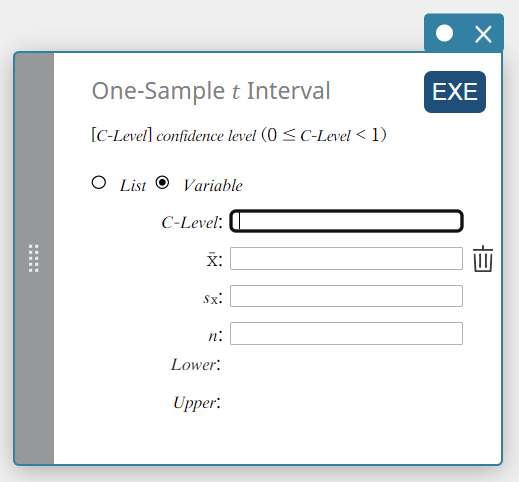
Intervalo \(t\) de uma amostra
Calcula o intervalo de confiança para a média populacional com base em uma média amostral e um desvio padrão amostral quando o desvio padrão populacional não é conhecido.

\(Lower = \overline{x}-t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
\(Upper = \overline{x}+t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)

Tipo de dados: Variável

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \overline{x} \) : média da amostra
  \(s_{x}\) : desvio padrão da amostra（\( s_{x} \ge 0 \)）
  \(n\) : tamanho da amostra (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)

Tipo de dados: Lista

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  Lista: lista onde os dados de amostra estão localizados
  Frequencia : frequência da amostra (1 ou nome da lista)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \( \overline{x} \) : média da amostra
  \( s_{x} \) : desvio padrão da amostra
  \( n \) : tamanho da amostra

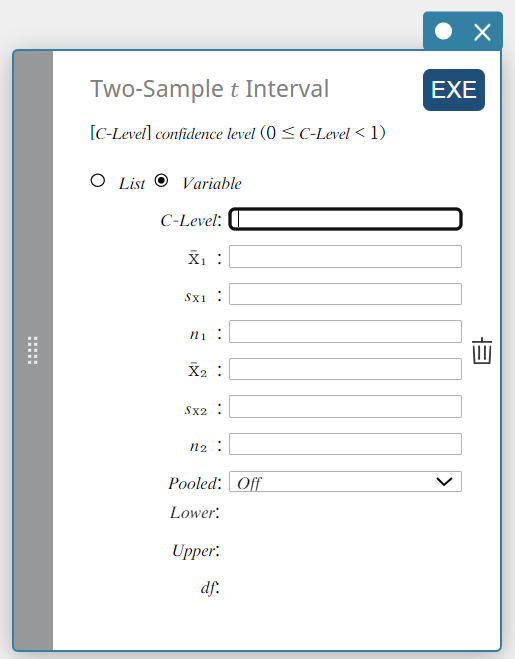
Intervalo \(t\) de duas amostras
Calcula o intervalo de confiança para a diferença entre as médias populacionais com base na diferença entre as médias amostrais e os desvios padrão amostrais quando os desvios padrão populacionais não são conhecidos.

• Quando os dois desvios padrão populacionais são iguais (agrupados)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  

• Quando os dois desvios padrão da população não são iguais (não agrupados)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{ \left( 1-C \right) ^2}{n_2-1}}\)
  \(C=\displaystyle \frac{\displaystyle \frac{{S_{x_1}}^2}{n_1}}{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1} + \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  

Tipo de dados: Variável

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \(s_{x_1}\) : desvio padrão amostral da amostra 1（\(s_{x_1} \ge 0\)）
  \( n_{1} \) : tamanho da amostra 1 (número inteiro positivo)
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \(s_{x_2}\) : desvio padrão amostral da amostra 2（\(s_{x_2} \ge 0\)）
  \( n_{2} \) : tamanho da amostra 2 (número inteiro positivo)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \(df\) : graus de liberdade
  \(s_p\) : desvio padrão da amostra agrupada

Tipo de dados: Lista

• Termos de entrada
  Nível C : nível de confiança（\(0 \le\) Nível C \(\lt 1\)）
  Lista(1) : lista onde os dados da amostra 1 estão localizados
  Lista(2) : lista onde os dados da amostra 2 estão localizados
  Frequência(1) : frequência da amostra 1 (1 ou nome da lista)
  Frequência(2) : frequência da amostra 2 (1 ou nome da lista)
  Agrupados : Ativado (variâncias iguais) ou Desativado (variâncias desiguais)

• Termos de saída
  Inferior: limite inferior do intervalo (borda esquerda)
  Superior: limite superior do intervalo (borda direita)
  \(df\) : graus de liberdade
  \( \overline{x}_{1} \) : média amostral dos dados da amostra 1
  \( \overline{x}_{2} \) : média amostral dos dados da amostra 2
  \( s_{x_{1}} \) : desvio padrão amostral da amostra 1
  \( s_{x_{2}} \) : desvio padrão amostral da amostra 2
  \(s_p\) : desvio padrão da amostra agrupada
  \( n_{1} \) : tamanho da amostra 1
  \( n_{2} \) : tamanho da amostra 2

Distribuição

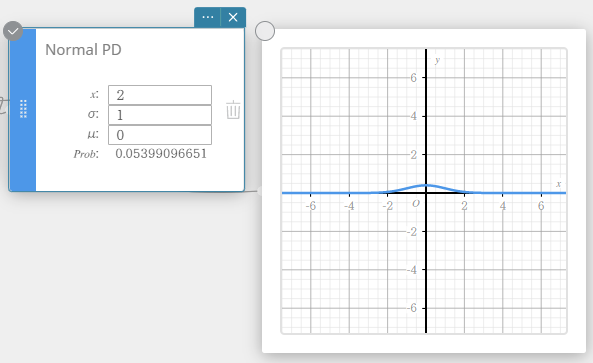
PD normal (densidade de probabilidade normal)
Calcula a densidade de probabilidade normal para um valor especificado.
Especificar σ = 1 e μ= 0 produz distribuição normal padrão.

\(\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \qquad (\sigma>0)\)

• Termos de entrada
  \( x \) : valor dos dados
  \( \sigma \) : desvio padrão da população (\( \sigma > 0 \)）
  \( \mu \) : média populacional

• Termos de saída
  Problema: densidade de probabilidade normal

CD normal (distribuição cumulativa normal)
Calcula a probabilidade cumulativa de uma distribuição normal entre um limite inferior ( a ) e um limite superior ( b ).

\(\displaystyle p=\frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{ \displaystyle -\frac{(x-\mu)^2}{2\sigma^2}}dx\)

• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \( \sigma \) : desvio padrão da população (\( \sigma > 0 \)）
  \(\mu\) : média populacional

• Termos de saída
  Problema : probabilidade de distribuição normal p
  z Baixo: valor limite inferior padronizado z
  z Acima: valor limite superior padronizado z

PD do aluno \(t\) (densidade de probabilidade do aluno \(t\))
Calcula a densidade de probabilidade t de Student para um valor especificado.


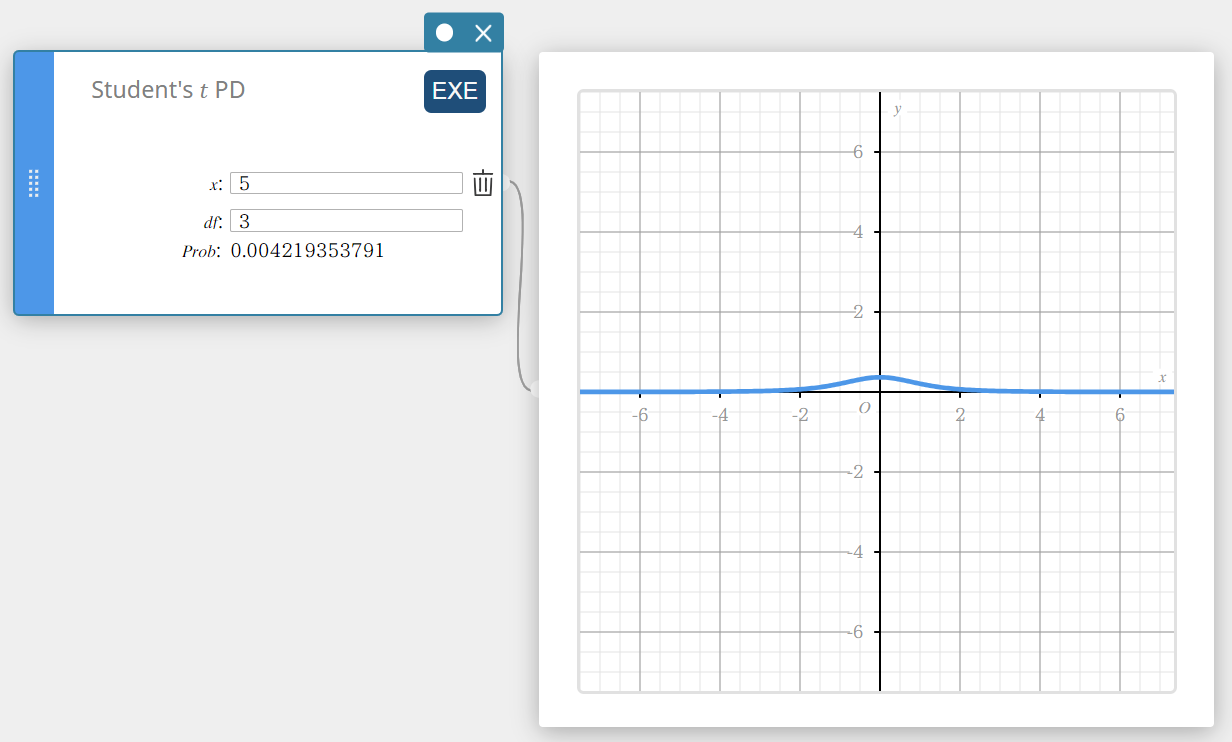
\(f(x)=\frac{\Gamma\left({\displaystyle\frac{df+1}2}\right)}{\Gamma\left({\displaystyle\frac{df}2}\right)}\times\frac{\left(1+{\displaystyle\frac{x^2}{df}}\right)^{-{\displaystyle\frac{df+1}2}}}{\sqrt{\pi\cdot df}}\)

• Termos de entrada
  \( x \) : valor dos dados
  \(df\) : graus de liberdade（\(df \gt 0\)）

• Termos de saída
  Problema : Densidade de probabilidade t do aluno

CD do aluno \(t\) (Distribuição cumulativa do aluno \(t\))
Calcula a probabilidade cumulativa de uma distribuição t de Student entre um limite inferior ( a ) e um limite superior ( b ).


\( p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{df+1}{2} \right) }{\Gamma \left(\displaystyle \frac{df}{2} \right) \sqrt{\pi \cdot df}}\int_a^b \left(\displaystyle 1+\frac{x^2}{df} \right) ^{-\displaystyle\frac{df+1}{2}}dx \)

• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \(df\) : graus de liberdade（\(df \gt 0\)）

• Termos de saída
  Problema : Distribuição t do aluno
  t Baixo: valor do limite inferior inserido
  t Acima : valor do limite superior inserido

\(\chi^2\) PD (\(\chi^2\) Densidade de probabilidade)
Calcula a densidade de probabilidade \(\chi^2\) para um valor especificado.


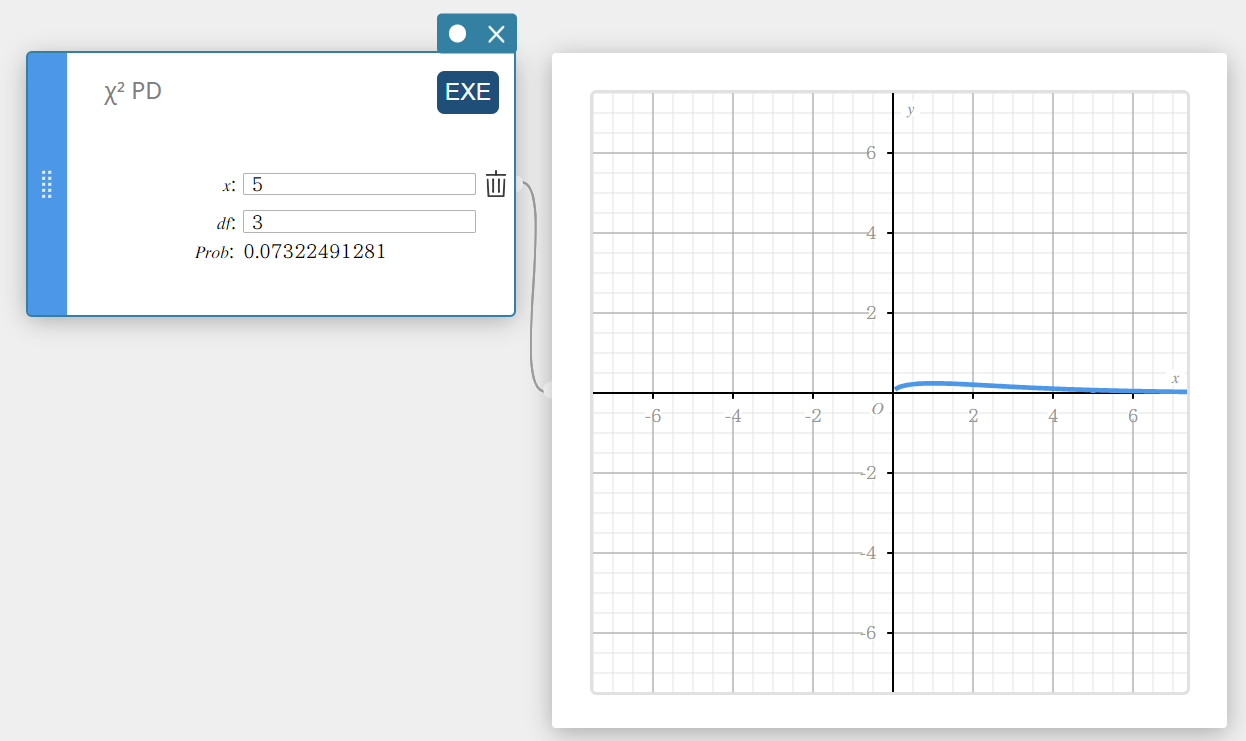
\(f \left( x \right) =\displaystyle\frac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}\)

• Termos de entrada
  \( x \) : valor dos dados
  \(df\) : graus de liberdade (número inteiro positivo)

• Termos de saída
  Problema : \(\chi^2\) densidade de probabilidade

\(\chi^2\) CD (\(\chi^2\) Distribuição Cumulativa)
Calcula a probabilidade cumulativa de uma distribuição \(\chi^2\) entre um limite inferior e um limite superior.


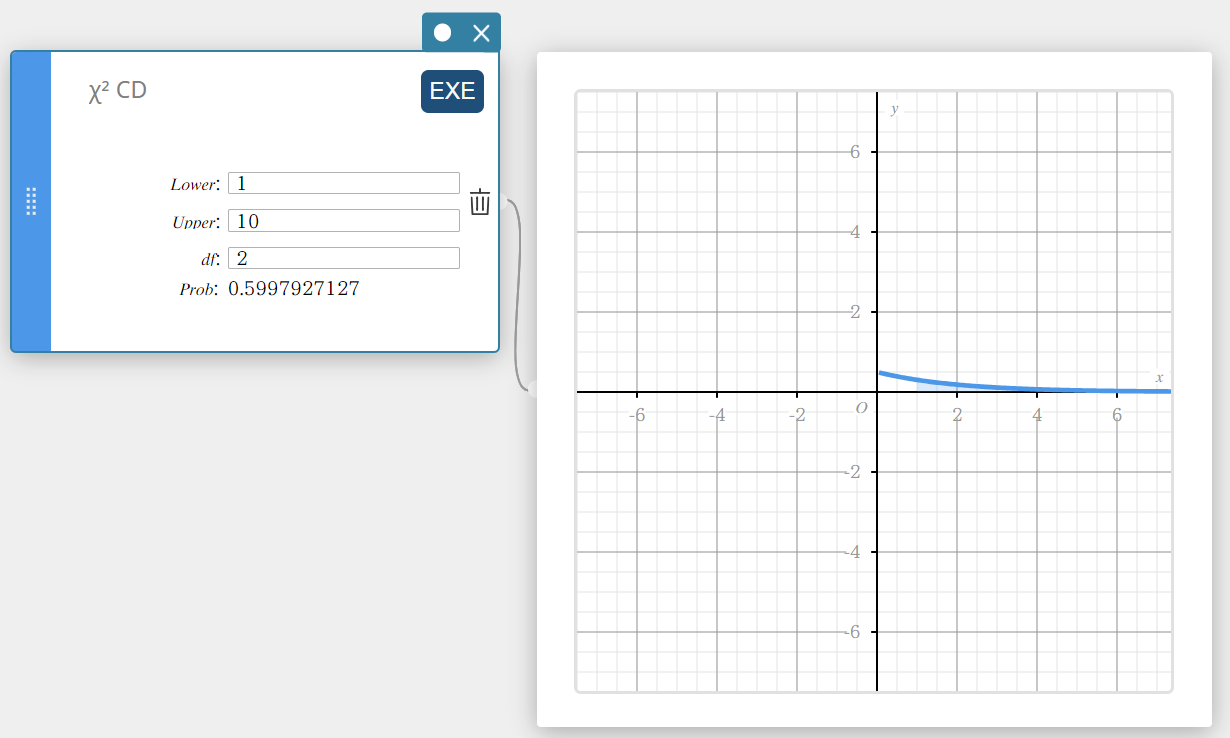
\(p=\cfrac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}\int_a^b x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}dx\)

• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \(df\) : graus de liberdade (número inteiro positivo)

• Termos de saída
  Problema : \(\chi^2\) probabilidade de distribuição

F PD (F densidade de probabilidade)
Calcula a densidade de probabilidade F para um valor especificado.


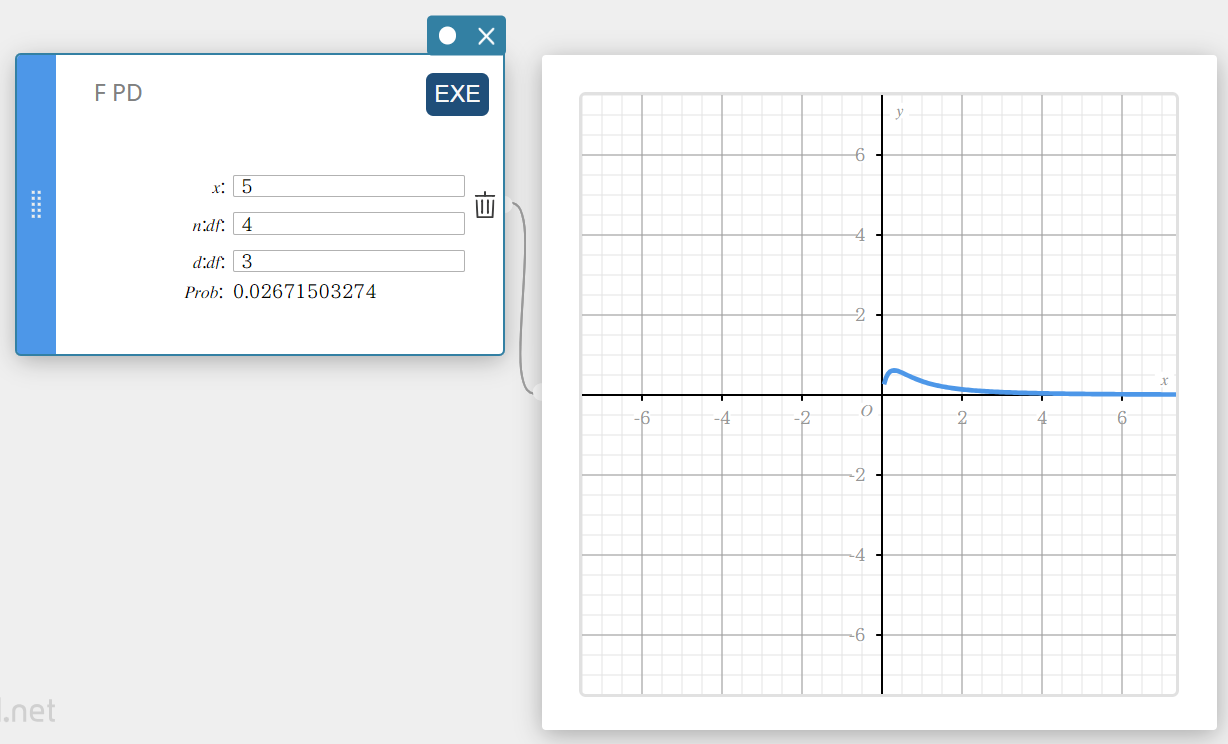
\(f(x)=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}\)

• Termos de entrada
  \( x \) : valor dos dados
  \( n:df \) : graus de liberdade do numerador (número inteiro positivo)
  \( d:df \) : graus de liberdade do denominador (número inteiro positivo)

• Termos de saída
  Problema : Densidade de probabilidade F

F CD (F Distribuição Cumulativa)
Calcula a probabilidade cumulativa de uma distribuiçãoF entre um limite inferior e um limite superior.


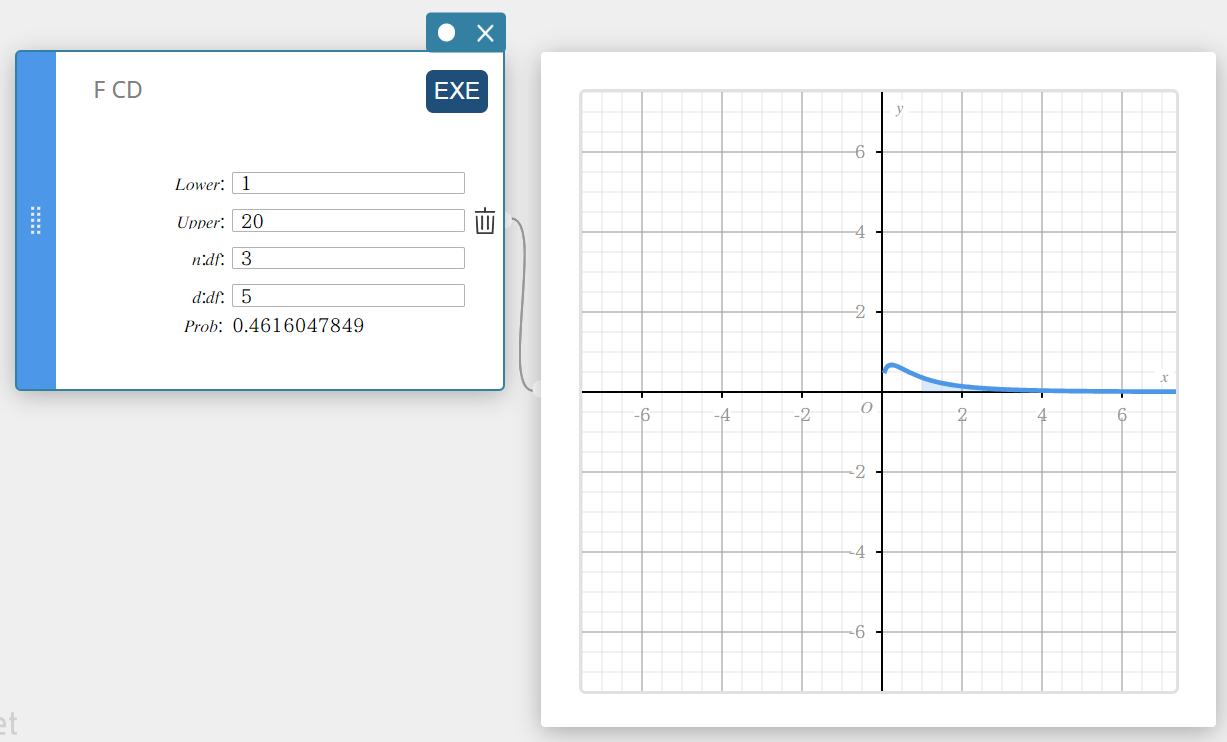
\(p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}\int_a^b x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}dx\)

• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \( n:df \) : graus de liberdade do numerador (número inteiro positivo)
  \( d:df \) : graus de liberdade do denominador (número inteiro positivo)

• Termos de saída
  Problema : F probabilidade de distribuição

PD binomial (probabilidade de distribuição binomial)
Calcula a probabilidade em uma distribuição binomial de que ocorrerá sucesso em uma tentativa específica.


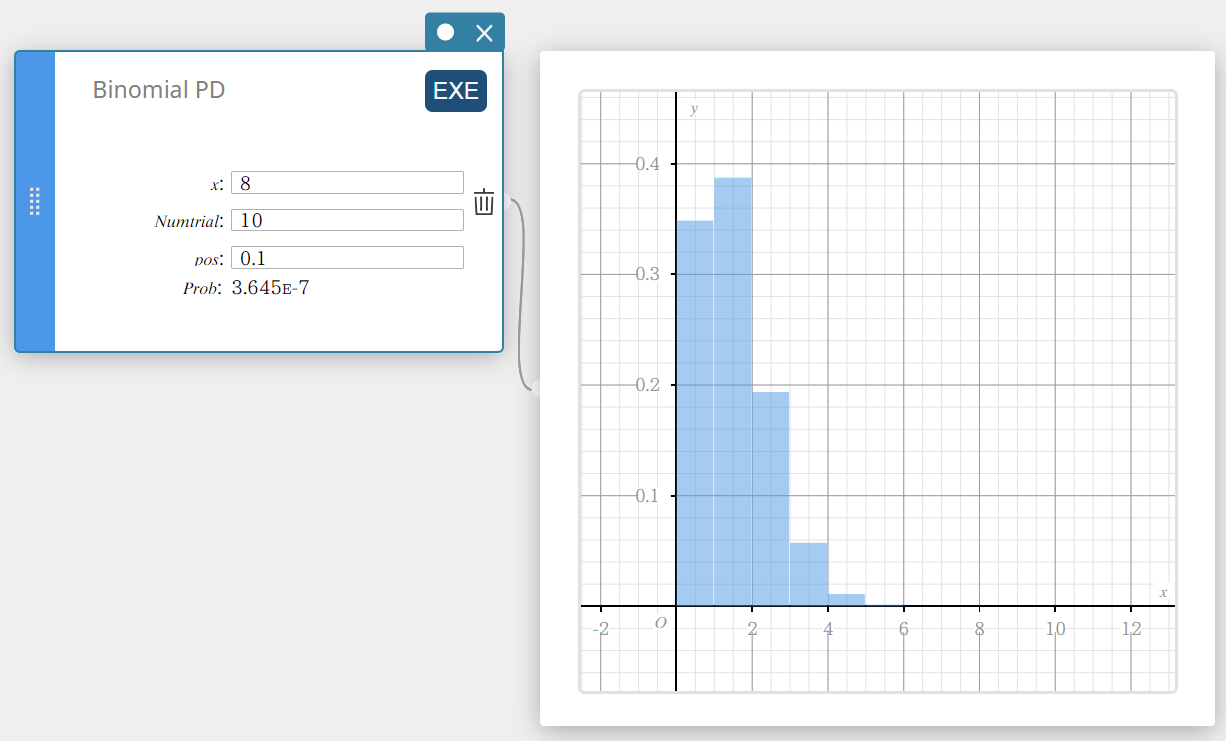
\(f(x)={}_nC_xp^x(1-p)^{n-x} \quad (x=0,1, \cdots,n)\)

\(p\) : probabilidade de sucesso（(0 \(≤\) p \(≤\) 1)
\(n\) : número de tentativas

• Termos de entrada
  \( x \) : tentativa especificada (número inteiro de 0 a n)
  Numtrial : número de tentativas n (inteiro, n ≥ 0)
  posição : probabilidade de sucesso p (0 \(≤\) p \(≤\) 1)

• Termos de saída
  Problema : probabilidade binomial

CD binomial (distribuição cumulativa binomial)
Calcula a probabilidade cumulativa em uma distribuição binomial de que o sucesso ocorrerá em ou antes de uma tentativa específica.

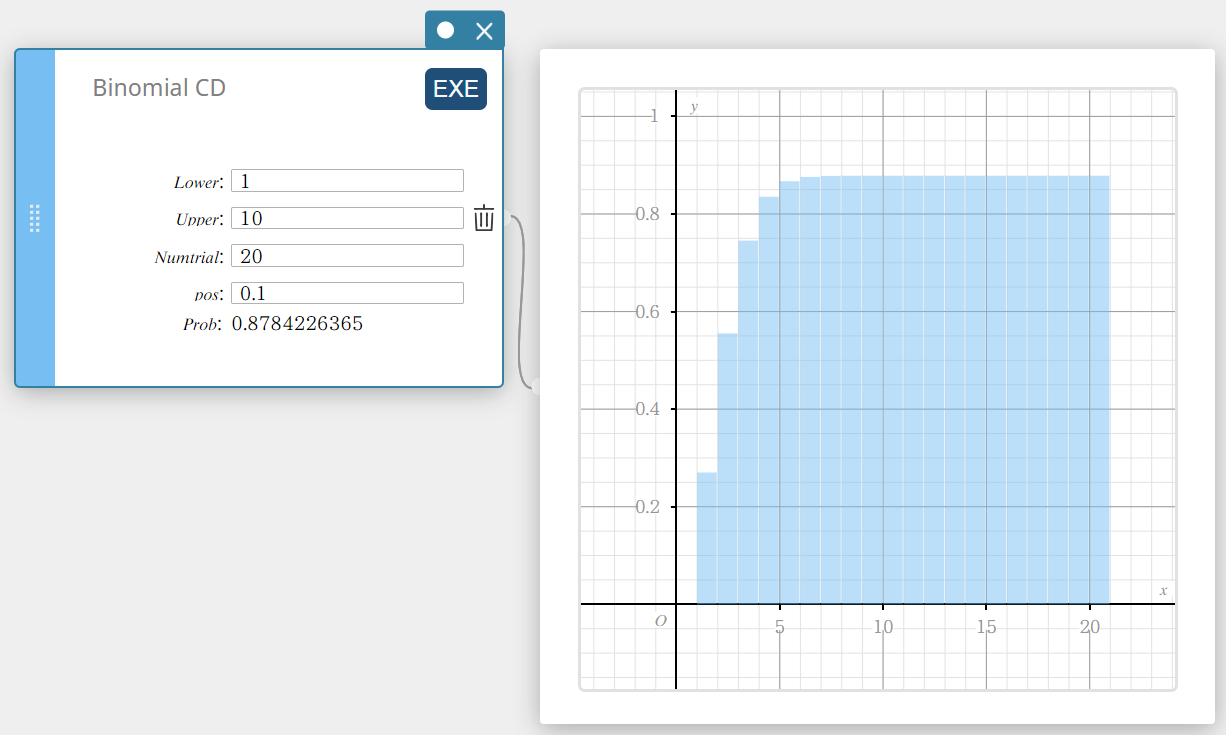
• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  Numtrial: número de tentativas n (inteiro, n \(≥\) 1)
  posição: probabilidade de sucesso p (0 \(≤\) p \(≤\) 1)

• Termos de saída
  Problema: probabilidade cumulativa binomial

Poisson PD (Probabilidade de Distribuição de Poisson)
Calcula a probabilidade em uma distribuição de Poisson de que ocorrerá sucesso em uma tentativa específica.

\(f(x)=\displaystyle\frac{e^{-\lambda} \lambda^x}{x!} \qquad (x=0,1,2,\cdots)\)

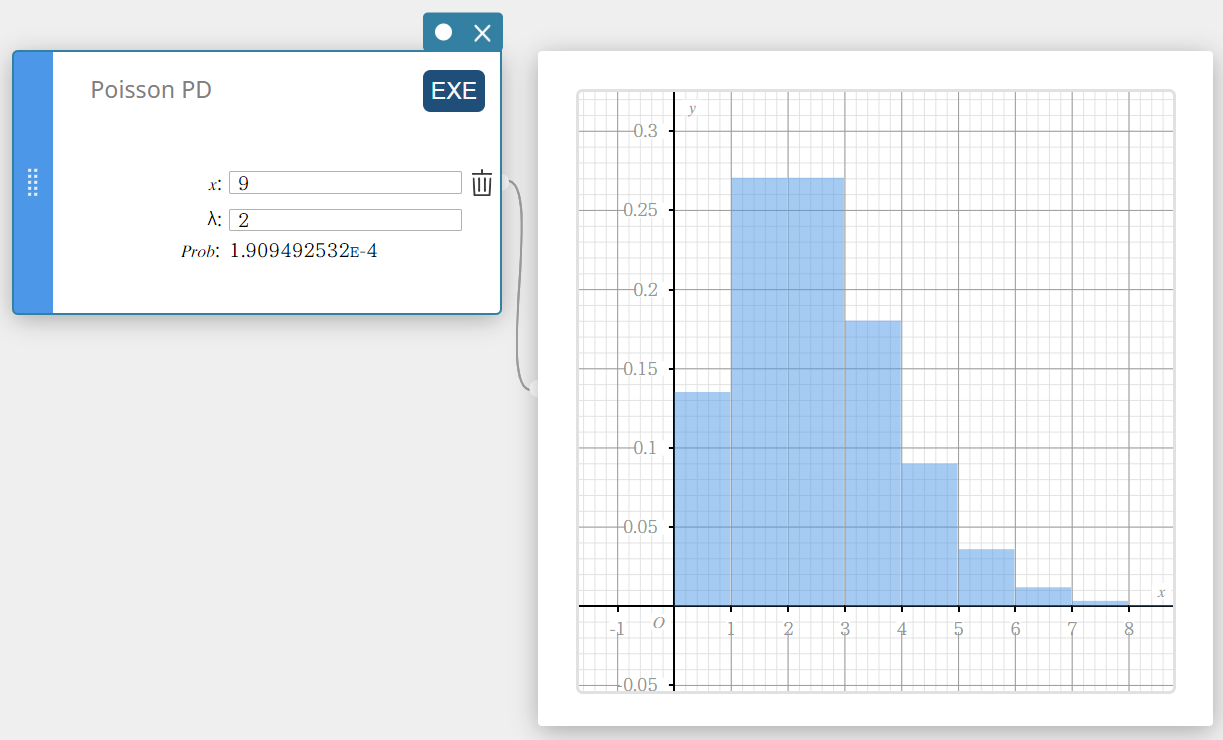
• Termos de entrada
  \( x \) : teste especificado (inteiro, x \(≥\) 0)
  \( \lambda \) : média（\(\lambda \gt 0\)）

• Termos de saída
  Problema: probabilidade de Poisson

CD Poisson (Distribuição Cumulativa Poisson)
Calcula a probabilidade cumulativa em uma distribuição de Poisson de que o sucesso ocorrerá em ou antes de uma tentativa específica.

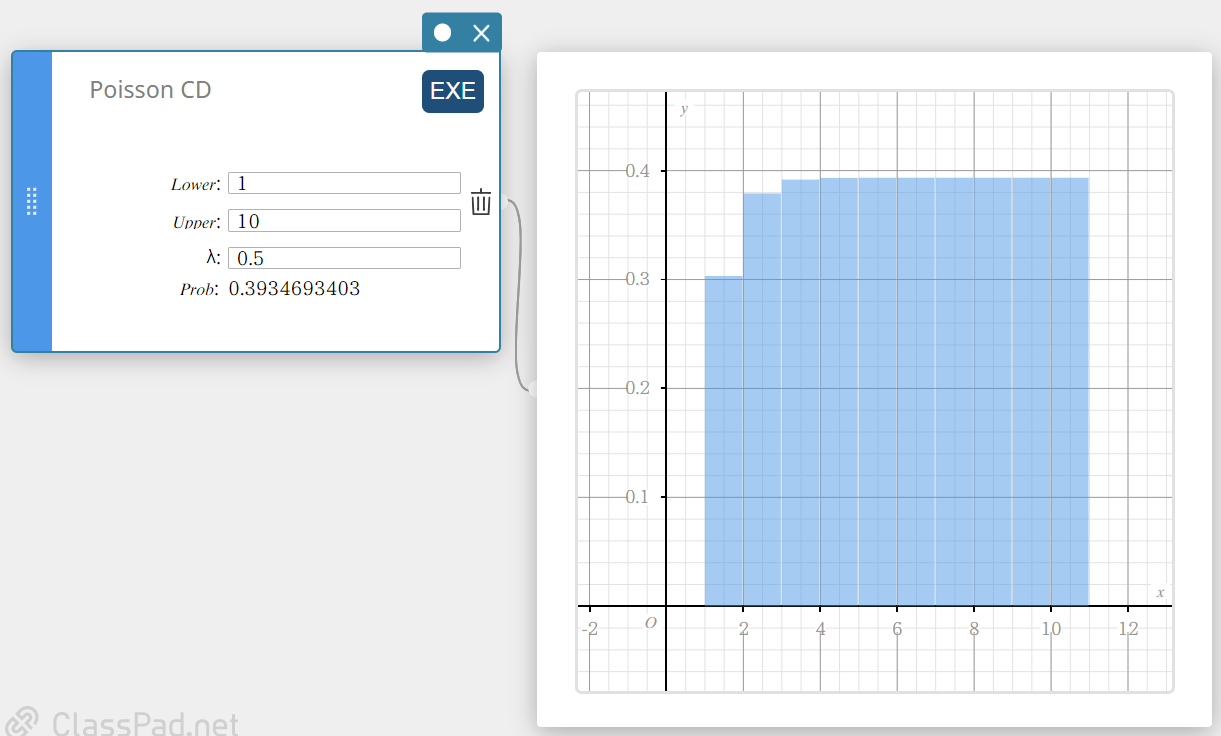
• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \( \lambda \) : média（\(\lambda \gt 0\)）

• Termos de saída
  Problema: probabilidade cumulativa de Poisson

PD Geométrica (Probabilidade de Distribuição Geométrica)
Calcula a probabilidade em uma distribuição geométrica de que o sucesso ocorrerá em uma tentativa específica.

\( f(x)=p(1-p)^{x-1} \qquad (x=1,2,3,\cdots) \)

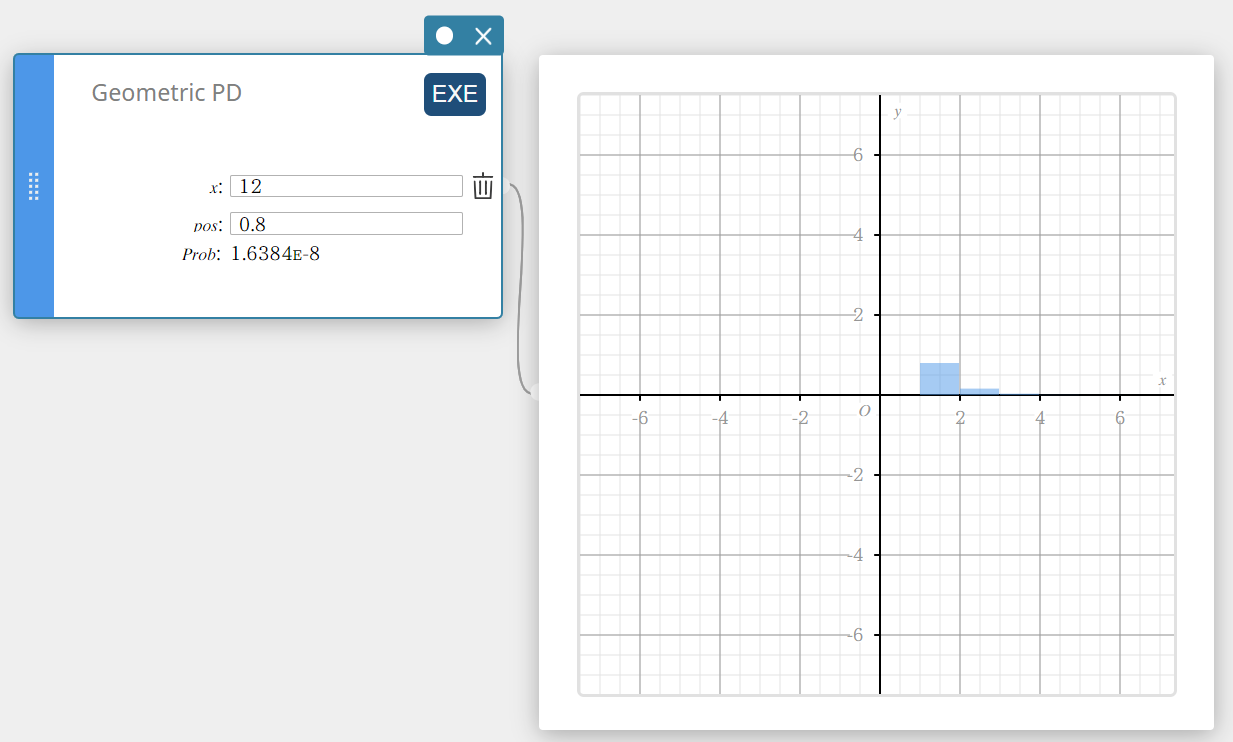
• Termos de entrada
  \( x \) : tentativa especificada (número inteiro positivo)
  posição: probabilidade de sucesso p (0 \(≤\) p \(≤\) 1)

• Termos de saída
  Problema: probabilidade geométrica

CD Geométrico (Distribuição Geométrica Cumulativa)
Calcula a probabilidade cumulativa em uma distribuição geométrica de que o sucesso ocorrerá em ou antes de uma tentativa específica.

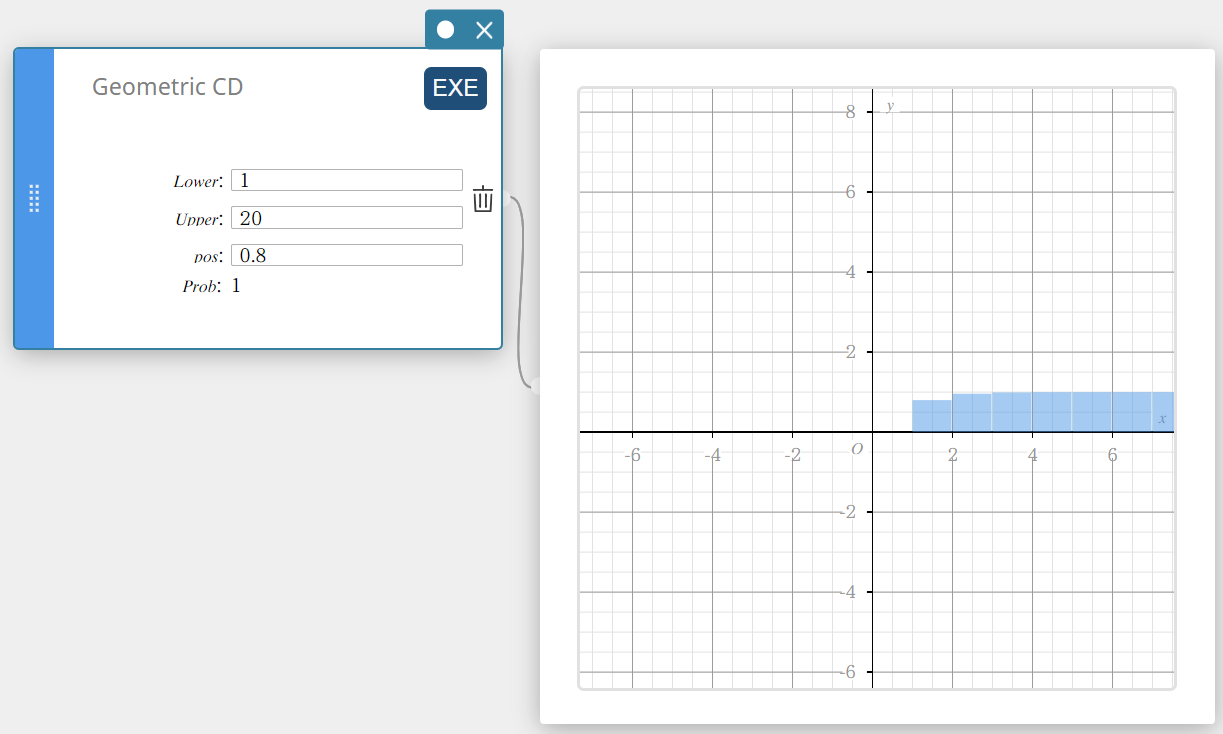
• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  posição: probabilidade de sucesso p (0 \(≤\) p \(≤\) 1)

• Termos de saída
  Problema: probabilidade cumulativa geométrica

PD Hipergeométrica (Probabilidade de Distribuição Hipergeométrica)
Calcula a probabilidade em uma distribuição hipergeométrica de que o sucesso ocorrerá em uma tentativa específica.

\( prob = \displaystyle\frac{ {}_MC_x \times {}_{N-M}C_{n-x} }{ {}_NC_n } \)

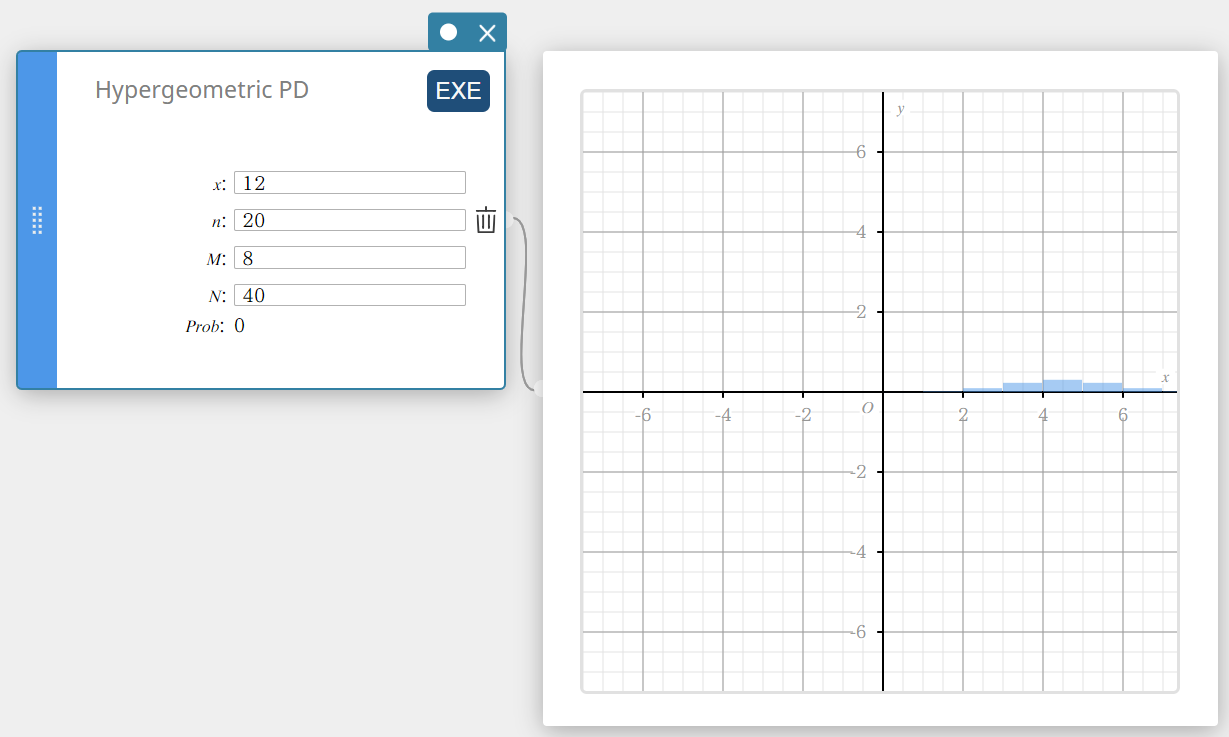
• Termos de entrada
  \(x\) : tentativa especificada (inteiro)
  \(n\) : número de ensaios da população (0 \(≤\) n inteiro)
  \(M\) : número de sucessos na população (0 \(≤\) M inteiro)
  \(N\) : tamanho da população ( n \(≤\) N , M \(≤\) N inteiro)

• Termos de saída
  Problema: probabilidade hipergeométrica

CD Hipergeométrico (Distribuição Cumulativa Hipergeométrica)
Calcula a probabilidade cumulativa em uma distribuição hipergeométrica de que o sucesso ocorrerá em ou antes de uma tentativa específica.

\( prob = \sum_{i=Lower}^{Upper}\displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

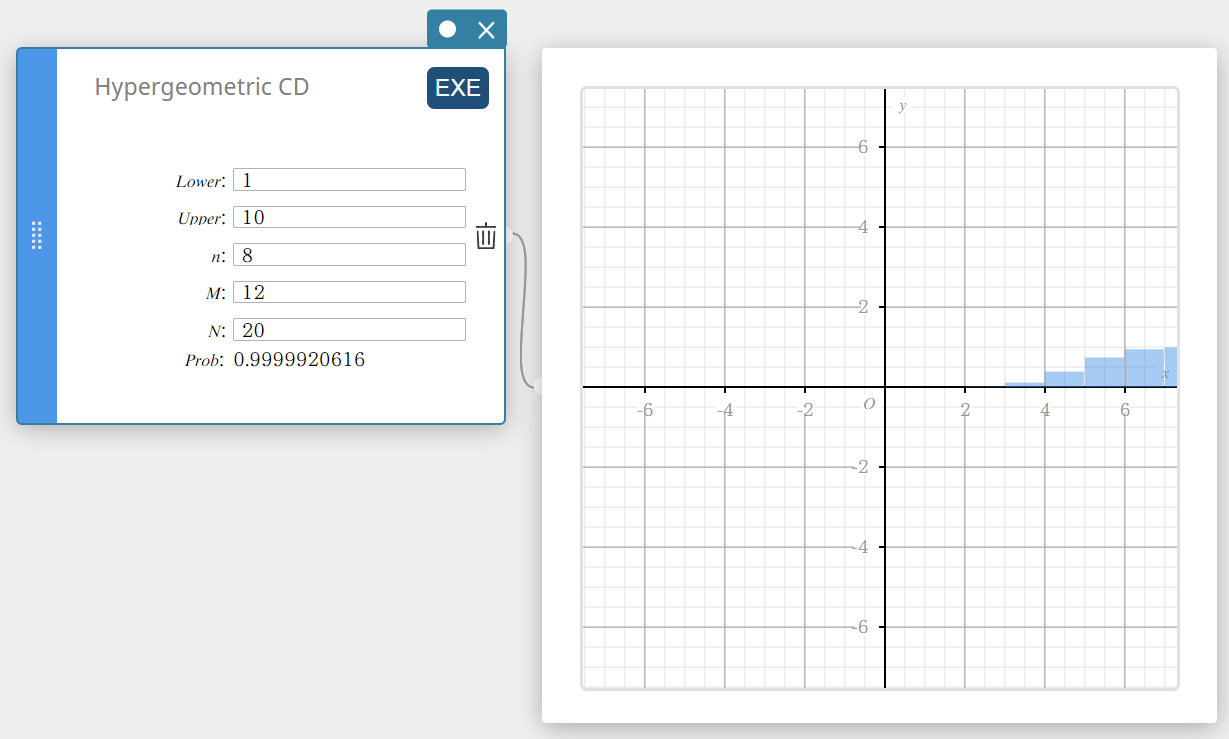
• Termos de entrada
  Inferior: limite inferior
  Superior: limite superior
  \(n\) : número de ensaios da população (0 \(≤\) n inteiro)
  \(M\) : número de sucessos na população (0 \(≤\) M inteiro)
  \(N\) : tamanho da população ( n \(≤\) N , M \(≤\) N inteiro)

• Termos de saída
  Problema: probabilidade cumulativa hipergeométrica

CD Normal Inverso (Distribuição Cumulativa Normal Inversa)
Calcula o(s) valor(es) limite de uma distribuição de probabilidade cumulativa normal para valores especificados.

Cauda: Esquerda
\( \int_{-\infty}^{\alpha}f(x)dx=p \)
O limite superior α é retornado.

Cauda: Direita
\( \int_{\alpha}^{+\infty}f(x)dx=p \)
O limite inferior α é retornado.

Cauda: Centro
\( \int_{\alpha}^{\beta}f(x)dx=p \qquad \left( \mu=\displaystyle\frac{\alpha+\beta}{2} \right) \)
O limite inferior α e o limite superior β são retornados.

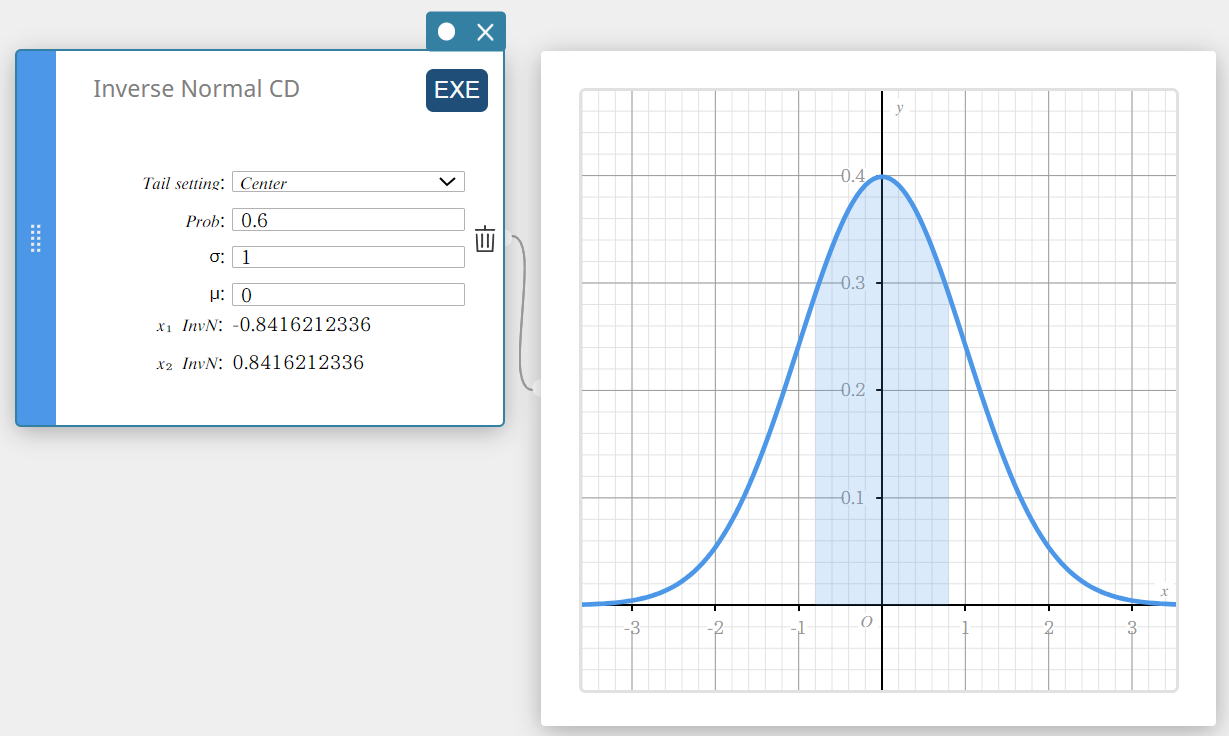
• Termos de entrada
  Configuração da cauda: especificação da cauda do valor de probabilidade (Centro, Esquerda, Direita)
  Problema: valor de probabilidade (0 \(≤\) Área \(≤\) 1)
  \( \sigma \) : desvio padrão da população（\( \sigma > 0 \)）
  \( \mu \) : média populacional

• Termos de saída
  \(x_1 {\rm InvN}\) : Limite superior quando Cauda: Esquerda
       Limite inferior quando Cauda: Direita ou Cauda: Centro
  \(x_2 {\rm InvN}\) : Limite superior quando Cauda: Centro

CD t inverso (distribuição cumulativa t inversa do aluno)
Calcula o valor do limite inferior de uma distribuição de probabilidade cumulativa t de Student para valores especificados.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Termos de entrada
  Problema: t probabilidade cumulativa (0 \(≤\) Área \(≤\) 1)
  \(df\) : graus de liberdade (df > 0)

• Termos de saída
  xInv: O valor do limite inferior de um Aluno’s t distribuição de probabilidade cumulativa

CD Inverso \(\chi^2\) (Distribuição Cumulativa Inversa \(\chi^2\))

Calcula o valor do limite inferior de um \(\chi^2\) distribuição de probabilidade cumulativa para valores especificados.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Termos de entrada
  Problema: \(\chi^2\) probabilidade cumulativa (0 \(≤\) Área \(≤\) 1)
  \(df\) : graus de liberdade (número inteiro positivo)

• Termos de saída
  \(x {\rm Inv}\) : O valor do limite inferior de um \(\chi^2\) distribuição de probabilidade cumulativa

CD F inverso (distribuição cumulativa F inversa)
Calcula o valor do limite inferior de uma distribuição de probabilidade cumulativa F para valores especificados.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Termos de entrada
  Problema: F probabilidade cumulativa (0 \(≤\) Área \(≤\) 1)
  \(n:df\) : graus de liberdade do numerador (número inteiro positivo)
  \(d:df\) : graus de liberdade do denominador (número inteiro positivo)

• Termos de saída
  xInv: O valor do limite inferior de uma distribuição de probabilidade cumulativa F

CD Binomial Inverso (Distribuição Cumulativa Binomial Inversa)
Calcula o número mínimo de tentativas de uma distribuição de probabilidade cumulativa binomial para valores especificados.

\( \sum_{x=0}^{m}f(x)\ge prob \)

• Termos de entrada
  Problema: probabilidade cumulativa binomial（\(0 \le\) Área \(\le 1\)）
  Numtrial: número de tentativas n (inteiro, n \(≥\) 0)
  posição: probabilidade de sucesso p (0 \(≤\) p \(≤\) 1)

• Termos de saída
  xInv: O valor do limite inferior de uma distribuição de probabilidade cumulativa F

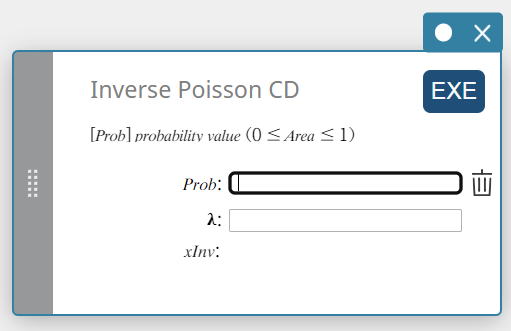
CD de Poisson Inverso (Distribuição Cumulativa de Poisson Inversa)
Calcula o número mínimo de tentativas de uma distribuição de probabilidade cumulativa de Poisson para valores especificados.

\( \sum_{x=0}^{m}f(x)\ge prob \)

• Termos de entrada
  Problema: probabilidade cumulativa de Poisson（\(0 \le\) Área \(\le 1\)）
  \( \lambda \) : média（\(\lambda \gt 0\)）

• Termos de saída
  xInv: O número mínimo de tentativas (o valor do limite superior) de uma distribuição de probabilidade cumulativa de Poisson

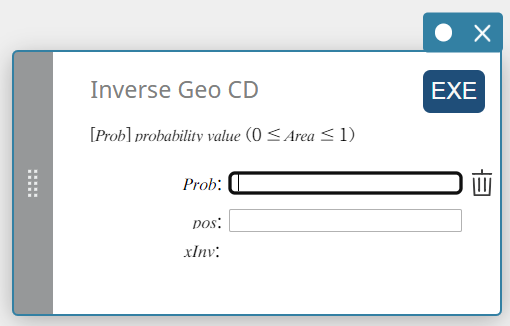
CD geográfico inverso (distribuição cumulativa geométrica inversa)
Calcula o número mínimo de tentativas de uma distribuição geométrica de probabilidade cumulativa para valores especificados.

\( \sum_{x=0}^{m}f(x)\ge prob \)

• Termos de entrada
  Problema: probabilidade cumulativa geométrica（\(0 \le\) Área \(\le 1\)）
  posição: probabilidade de sucesso p（\(0 \le p \le 1\)）

• Termos de saída
  xInv: O número mínimo de tentativas (o valor do limite superior) de uma distribuição geométrica de probabilidade cumulativa

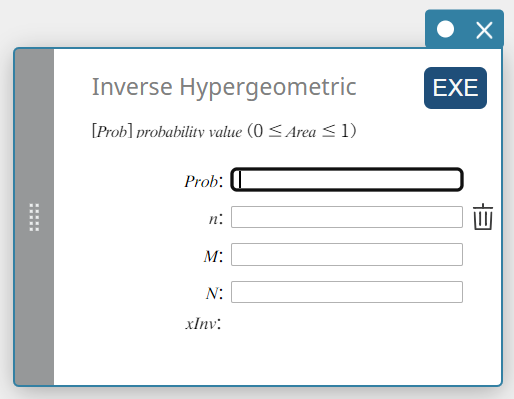
Hipergeométrica Inversa (Distribuição Cumulativa Hipergeométrica Inversa)
Calcula o número mínimo de tentativas de uma distribuição de probabilidade cumulativa hipergeométrica para valores especificados.

\( prob \le \sum_{i=0}^{X} \displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

• Termos de entrada
  Problema: probabilidade cumulativa hipergeométrica（\(0 \le\) Área \(\le 1\)）
  \(n\) : número de ensaios da população (0 \(≤\) n inteiro)
  \(M\) : número de sucessos na população (0 \(≤\) M inteiro)
  \(N\) : tamanho da população ( n \(≤\) N , M \(≤\) N inteiro)

• Termos de saída
  xInv: O número mínimo de tentativas (o valor do limite superior) de uma distribuição de probabilidade cumulativa hipergeométrica

Outros gráficos estatísticos

Gráfico de dispersão
Este gráfico compara a proporção acumulada de dados com uma proporção acumulada de distribuição normal. Se o gráfico de dispersão estiver próximo de uma linha reta, os dados serão aproximadamente normais. Um desvio da linha reta indica um afastamento da normalidade.

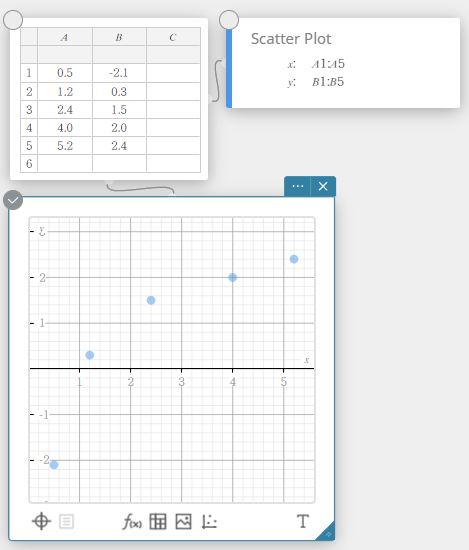
Gráfico de caixa e bigode
Este tipo de gráfico permite ver como um grande número de itens de dados está agrupado em intervalos específicos. Uma caixa inclui todos os dados em uma área do primeiro quartil (\({\rm Q}_1\)) para o terceiro quartil (\({\rm Q}_3\)), com uma linha desenhada na mediana (\({\rm Med}\)). Linhas (chamadas bigodes) estendem-se de cada extremidade da caixa até o mínimo (\({\rm minX}\)) e máximo (\({\rm maxX}\)) dos dados.

Histograma
Um histograma mostra a frequência (distribuição de frequência) de cada classe de dados como uma barra retangular. As classes estão no eixo horizontal, enquanto a frequência está no eixo vertical. Se necessário, você pode alterar o valor inicial (\(HStart\)) e valor do passo (\(HStep\)) do histograma.

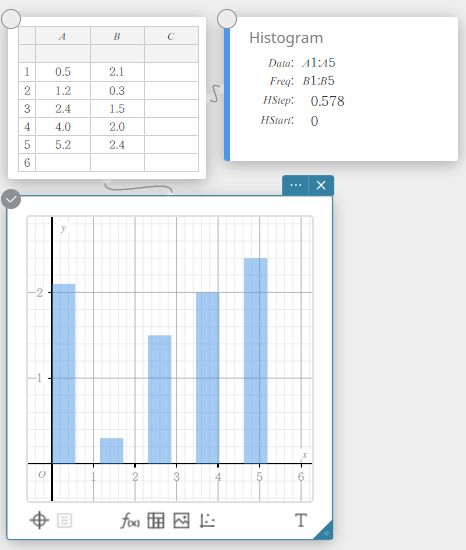
Gráfico de pizza
Você pode desenhar um gráfico circular com base nos dados de uma lista específica.

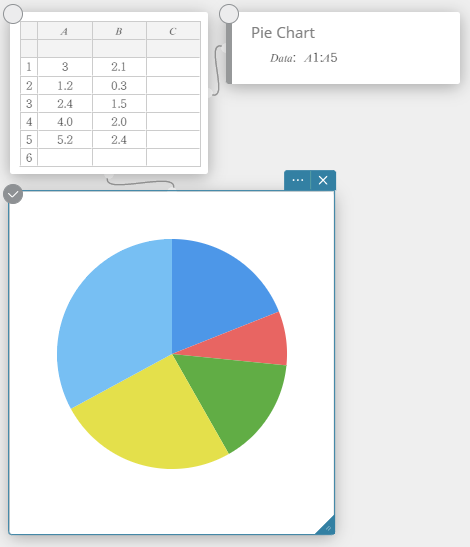
Gráfico de pontos
Os valores na Coluna A (eixo horizontal) representam números de compartimento, enquanto os valores na Coluna B (eixo vertical) representam a contagem de pontos de dados em cada compartimento. Um ponto é plotado para cada ponto de dados em uma caixa.