Geavanceerd

solve

Geeft de oplossing van een vergelijking of ongelijkheid weer.
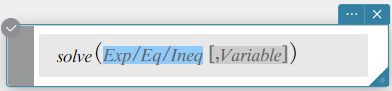
Syntax 1: solve(Exp/Eq/Ineq [, variabele] [ ) ]

• “\(x\)” is de standaard wanneer u “[, Variabele]” weglaat.

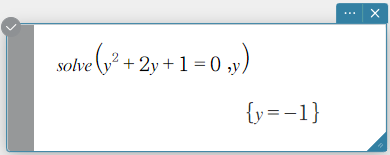
Syntax 2: solve(Exp/Eq/Ineq\(≠\), Variabele[, waarde, ondergrens, bovengrens] [ ) ]

• Deze opdracht is alleen geldig voor vergelijkingen en \(≠\) uitdrukkingen wanneer “waarde” en de items die erop volgen ingesloten zijn. In dat geval geeft deze opdracht een geschatte waarde weer.
• Een juiste waarde wordt weergegeven wanneer u “waarde” en de daaropvolgende items weglaat. Wanneer een juiste waarde echter niet kan worden verkregen, wordt een geschatte waarde weergegeven voor uitsluitend vergelijkingen op basis van de aanname dat waarde = 0, ondergrens = – ∞ en bovengrens = ∞.

Syntax 3: solve({Exp-1/Eq-1, …, Exp-N/Eq-N}, {Variabele-1, …, Variabele-N} [ ) ]

• Wanneer “Exp” het eerste argument is, wordt de vergelijking Exp = 0 verondersteld.

Syntax 4:
Door een vectorvergelijking binnen de solve(-opdracht in te voeren kunt u de relatie tussen 2 objecten (punten, lijnen, vlakken of bollen) berekenen. Hier worden 4 typische voorbeelden van syntax getoond voor het berekenen van een vectorvergelijking met de solve(-opdracht.

De onderstaande syntax toont een kolomvector met 3 (of 2) elementen tussen Vct-1 en Vct-6), met s, t, u en v als de parameters.
solve(Vct-1 + s * Vct-2 [= Vct-3, {variabele-1}])

• Als de rechterkant van de vergelijking (= Vct-3) in bovenstaande syntax wordt weggelaten, wordt verondersteld dat alle elementen aan de rechterkant 0-vectoren zijn.
  solve(Vct-1 + s * Vct-2 = Vct-3 + t * Vct-4, {variabele-1, variabele-2})
  solve(Vct-1 + s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5, {variabele-1, variabele-2, variabele-3})
  solve(Vct-1 + s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5 + v * Vct-6, {variabele-1, variabele-2, variabele-3, variabele-4})
• Variabelen (variabele 1 tot en met variabele 4) kunnen worden ingevoerd in de elementen van elke vector (Vct-1 tot en met Vct-6) in de vier bovenstaande syntaxen die voor die variabelen moeten worden berekend.
  

dSolve

Lost gewone differentiaalvergelijkingen van de eerste, tweede of derde orde op, of een systeem van differentiaalvergelijkingen van de eerste orde.
Syntax: dSolve(Eq, onafhankelijke variabele, afhankelijke variabele [, initiële voorwaarde-1, initiële voorwaarde-2][, initiële voorwaarde-3, initiële voorwaarde-4][, initiële voorwaarde-5, initiële voorwaarde-6] [ ) ]
dSolve({Eq-1, Eq-2}, onafhankelijke variabele, {afhankelijke variabele-1, afhankelijke variabele-2} [, initiële voorwaarde-1, initiële voorwaarde-2, initiële voorwaarde-3, initiële voorwaarde-4] [ ) ]

• Als u de initiële voorwaarden weglaat, bevat de oplossing willekeurige constanten.
• Voer alle vergelijkingen van initiële voorwaarden in die de syntax Var = Exp gebruiken. Elke initiële voorwaarde die een andere syntax gebruikt, wordt genegeerd.

taylor

Zoekt een Taylor-multinominiaal voor een uitdrukking met betrekking tot een specifieke variabele.
Syntax: taylor (Exp/List, variabele, volgorde [,middelpunt] [ ) ]

• Nul is de standaard wanneer u “[, middelpunt]” weglaat.

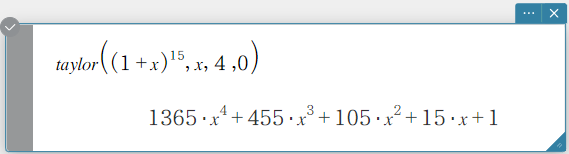
laplace, invLaplace

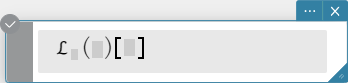
“laplace” is de opdracht voor de Laplace-transformatie en invLaplace is de opdracht voor het omgekeerde van Laplace-transformatie.
Syntax: laplace \(\mathcal{L}_t (f(t))[s]\)
　　\(f(t)\): uitdrukking
　　\(t\): Variabele volgens dewelke de uitdrukking wordt getransformeerd
　　\(s\): parameter van de transformatie
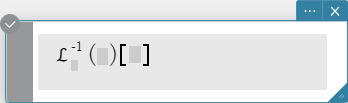
　　　invLaplace \(\mathcal{L}_s^{-1} (L(s))[t]\)
　　\(L(s)\): uitdrukking
　　\(s\): Variabele volgens dewelke de uitdrukking wordt getransformeerd
　　\(t\): parameter van de transformatie

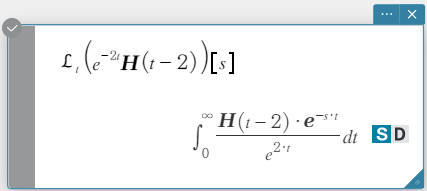
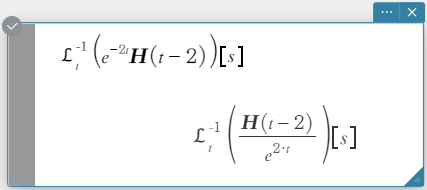
fourier, invFourier

“fourier” is de opdracht voor de Fourier-transformatie en “invFourier” is de opdracht voor de omgekeerde Fourier-transformatie.
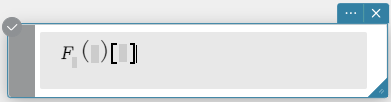
Syntax: fourier \(~ Ϝ_x (f(x))[w]\)
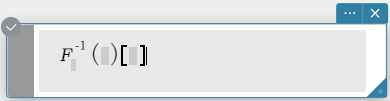
　　invFourier \(~ Ϝ_w^{-1} (f(w))[x]\)
　　\(x\): Variabele volgens dewelke de uitdrukking wordt getransformeerd
　　\(w\): parameter van de transformatie

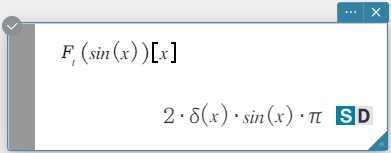
FFT, IFFT

“FFT” is de opdracht voor de snelle Fourier-transformatie en “IFFT” is de opdracht voor de omgekeerde snelle Fourier-transformatie.
De \(2^n\) gegevenswaarde is vereist voor FFT en IFT. FFT en IFFT worden numeriek berekend.
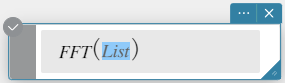
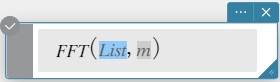
Syntax: FFT(list) of FFT(list, m)
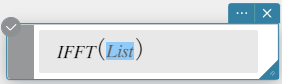
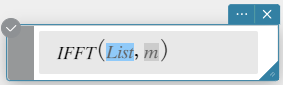
　　IFFT(list) of IFFT(list, m)

• De gegevensgrootte moet \(2^n\) zijn voor n = 1, 2, 3, …
• De waarde voor m is optioneel. Ze kan van 0 tot 2 bedragen en geeft aan welke FFT-parameter moet worden gebruikt: 0 (Signaalverwerking), 1 (Zuivere wiskunde), 2 (Gegevensanalyse).