Statistische berekeningen

inhoudsopgave

Basisbewerkingen van statistische berekeningen
Statistische gegevenswaarden bewerken
Gegevenswaarden voor een statistische berekening selecteren
Statistische berekeningen met één variabele uitvoeren
Een regressiegrafiek tekenen
Een histogram tekenen
Een box-en-whiskerdiagram tekenen
Een cirkelgrafiek tekenen
Bewerkingen van spreidingsdiagram
Een Z-test van één steekproef uitvoeren
Statistische berekeningen en grafieken

Basisbewerkingen van statistische berekeningen

• Waarden invoeren in een sticky note voor statistische gegevens
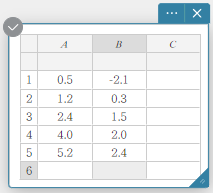
  In het voorbeeld in dit gedeelte worden de gegevenswaarden uit de onderstaande tabel ingevoerd in de cellen A1 t/m B5 van een sticky note voor statistische gegevens.

	A	B
1	\(0.5\)	\(-2.1\)
2	\(1.2\)	\(0.3\)
3	\(2.4\)	\(1.5\)
4	\(4.0\)	\(2.0\)
5	\(5.2\)	\(2.4\)

1. Klik op in het menu voor sticky notes.
   
   Er verschijnt een sticky note voor statistische gegevens.
   
   Cel A1 wordt geselecteerd voor invoer op dit moment.
2. Voer \(0.5\) in cel A1 in en druk vervolgens op [Enter].
   Cel A2 wordt geselecteerd voor invoer.
3. Voer \(1.2\) in cel A2 in en druk vervolgens op [Enter].
   Cel A3 wordt geselecteerd voor invoer. Voer op dezelfde wijze de gegevens in tot en met cel A5.
4. Klik op cel B1.
   Cel B1 wordt geselecteerd voor invoer.
5. Voer \(-2.1\) in cel B1 in en druk vervolgens op [Enter].
   Cel B2 wordt geselecteerd voor invoer. Kolom C zal nu ook worden aangemaakt (zie onderstaande OPMERKING).
6. Voer \(0.3\) in cel B2 in en druk vervolgens op [Enter].
   Cel B3 wordt geselecteerd voor invoer. Voer op dezelfde wijze de gegevens in tot en met cel B5.
   
   OPMERKING
   Wanneer u een waarde invoert in de meest rechtse kolom, wordt er automatisch een kolom toegevoegd rechts ervan.
   
   U kunt de cellen onder de kolomlabels (A, B, C, …) gebruiken om een lijstnaam voor elke kolom in te voeren. Zie voor details “Een naam aan een lijst toewijzen”.

• Gegevenswaarden voor een statistische berekening selecteren

1. Volg de procedure onder “Waarden invoeren in een sticky note voor statistische gegevens” om gegevenswaarden in te voeren.
   

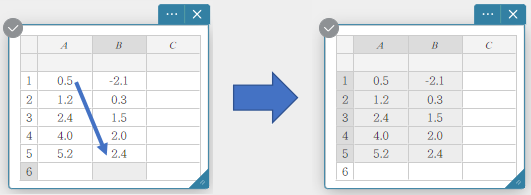
   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)

2. Sleep met uw computermuis van cel A1 naar cel B5.
   Hiermee selecteert u het celbereik van cel A1 tot en met cel B5.
   

OPMERKING
U kunt een volledige kolom selecteren door op het kolomnummer ervan te klikken.
U kunt een volledige rij selecteren door op het rijnummer ervan te klikken.
U kunt klikken of slepen tussen kolomnummers en de gegevens in die kolommen gebruiken om een grafiek te tekenen.
In dit geval kunt u na het tekenen van de grafiek ook de vervolgkeuzelijst van de sticky note van de grafiek gebruiken om andere kolomnummers te selecteren en de grafiek opnieuw te tekenen.

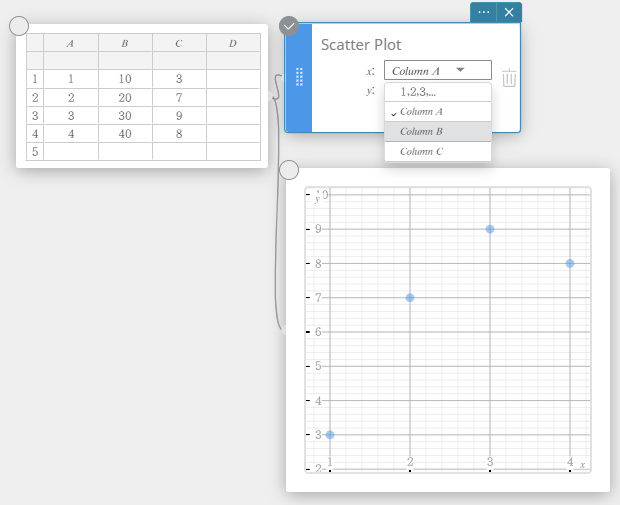
• Statistische berekeningen uitvoeren

In dit voorbeeld voeren we statistische berekeningen met twee variabelen uit en tekenen we een spreidingsdiagram en een lineaire regressiegrafiek.

1. Voer de gegevenswaarden in de onderstaande tabel in en selecteer vervolgens alle gegevens.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)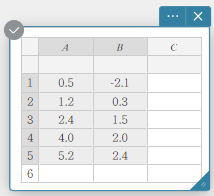

   

2. Klik op het schermtoetsenbord op [Berekening] – [Twee-variabelen].
   
   De resultaten van statistische berekeningen met twee variabelen worden weergegeven.
   
3. Klik op het schermtoetsenbord op .
   
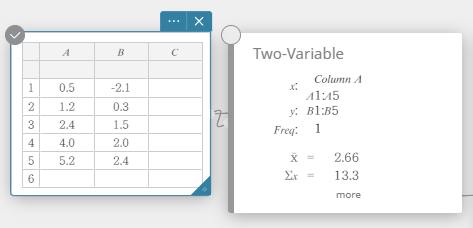
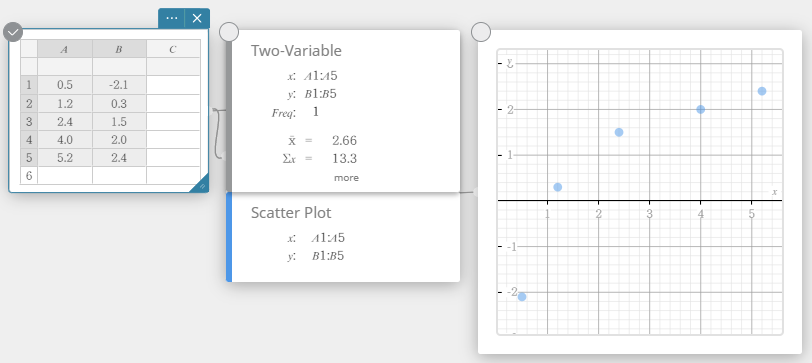
4. Klik op het schermtoetsenbord op [Grafiek] – [Spreidingsdiagram].
   
   Er wordt een sticky note voor een spreidingsdiagram aangemaakt en tegelijkertijd wordt er een scheidingsdiagram op de sticky note voor grafieken getekend.
   
5. Klik op het schermtoetsenbord op .
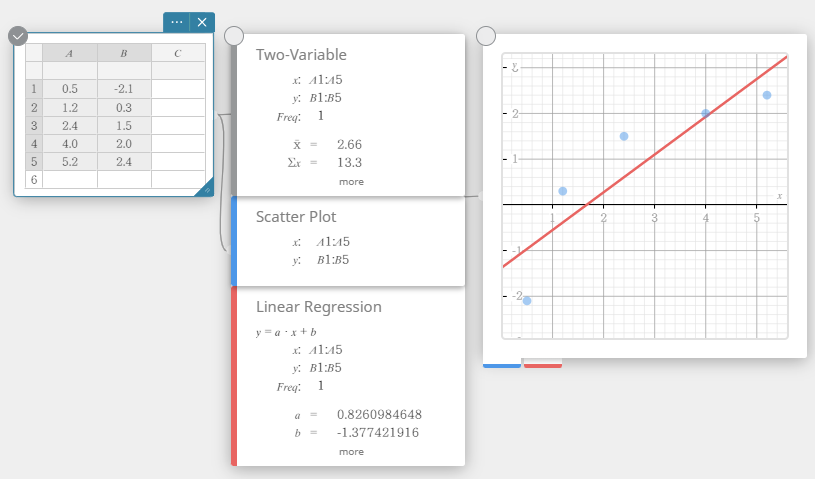
6. Klik op het schermtoetsenbord op [Regressie] – [Lineaire regressie].
   
   Er wordt een sticky note voor lineaire regressie aangemaakt en tegelijkertijd wordt er een lineaire regressiegrafiek op de sticky note voor grafieken getekend.
   

Statistische gegevenswaarden bewerken

• Gegevenswaarden corrigeren

1. Klik op de cel die de gegevenswaarde bevat die u wilt verbeteren.
   
2. Voer de nieuwe gegevenswaarde in en druk vervolgens op [Enter].
   

• Een rij invoegen

1. Klik met de rechtermuisknop op het nummer van de rij waar u een nieuwe rij wilt invoegen.
   Er verschijnt een menu.
   
2. Klik op [Insert].
   Er wordt een rij ingevoegd.
   

• Een kolom invoegen

1. Klik met de rechtermuisknop op de hoofding van de kolom waar u een nieuwe kolom wilt invoegen.
   Er verschijnt een menu.
   
2. Klik op [Insert].
   Er wordt een kolom ingevoegd.
   

• Een rij wissen

1. Klik met de rechtermuisknop op het nummer van de rij die u wilt wissen.
   Er verschijnt een menu.
   
2. Klik op [Delete].
   De rij wordt gewist.
   

• Een kolom wissen

1. Klik met de rechtermuisknop op de hoofding van de kolom die u wilt wissen.
   Er verschijnt een menu.
   
2. Klik op [Delete].
   De kolom wordt gewist.
   

• Een naam aan een lijst toewijzen

Wanneer u een naam aan een lijst toewijst, kunt u de naam gebruiken in tests en andere statistische berekeningen. Namen van lijsten worden ingevoerd in de cellen onder de kolomnamen.

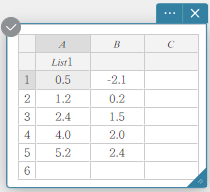
Voorbeeld: De naam “List1” aan kolom A toewijzen

1. Dubbelklik op de cel onder A.
   De cel wordt geselecteerd voor invoer van de lijstnaam.
   
2. Voer de lijstnaam “List1” in en druk vervolgens op [Enter].
   “List1” wordt ingesteld als lijstnaam van kolom A.
   
   OPMERKING
   De volgende regels zijn van toepassing op lijstnamen.
   － Lijstnamen kunnen max. 8 bytes lang zijn.
   － De volgende tekens mogen in een lijstnaam worden gebruikt: Hoofdletters en kleine letters, subscript tekens en cijfers.
   － Lijstnamen zijn hoofdlettergevoelig. Zo wordt bijvoorbeeld elk van de volgende namen beschouwd als een andere lijstnaam: abc, Abc, aBc, ABC.

Gegevenswaarden voor een statistische berekening selecteren

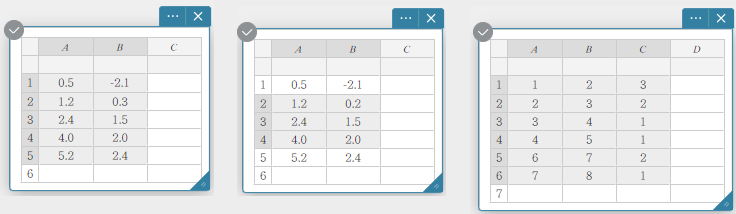
U kunt een celbereik selecteren door de muisaanwijzer erover te slepen.

Voorbeelden van gegevensselectie

OPMERKING
U kunt een volledige kolom selecteren door op het kolomnummer ervan te klikken.
U kunt een volledige rij selecteren door op het rijnummer ervan te klikken.

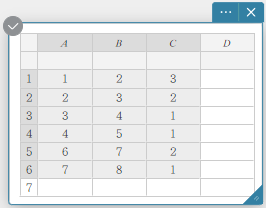
Statistische berekeningen kunnen worden uitgevoerd als het bereik van geselecteerde cellen één of meer lege cellen bevat.
Maximaal drie kolommen kunnen voor statistische berekeningen worden gebruikt. Statistische berekeningen kunnen niet worden uitgevoerd als er meer dan drie kolommen geselecteerd zijn.

Statistische berekeningen met één variabele uitvoeren

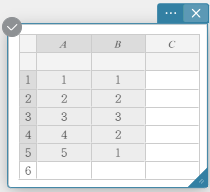
1. Voer de gegevenswaarden in de onderstaande tabel in, met de gegevens in kolom A en de frequentie in kolom B.
   

   Data	Frequency
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Sleep van cel A1 tot cel B5 om het celbereik ertussen te selecteren.
   

3. Klik op het schermtoetsenbord op [Berekening] – [Eén-variabele].
   De resultaten van statistische berekeningen met één variabele worden getoond.
   
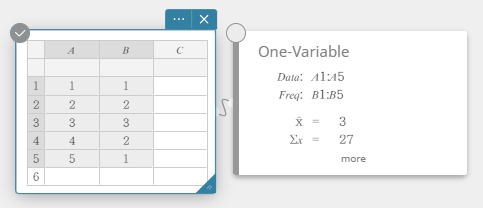
4. Om andere verborgen items van de berekeningsresultaten te tonen, klikt u op [meer] op de sticky note voor statistische berekeningen.
   De verborgen berekeningsresultaten worden getoond.
   Klik op [Verbergen] om de sticky note voor statistische berekeningen terug te brengen tot zijn gereduceerde afmeting.
   

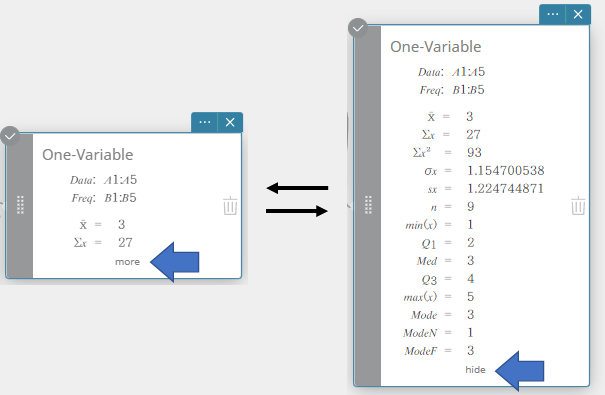
Als u een statistische berekening met één variabele uitvoert, worden de onderstaande resultaten weergegeven.
\(\bar{\rm x}\)　　　steekproefgemiddelde
\(\Sigma {\rm x}\)　　 som van de gegevens
\(\Sigma {\rm x}^2\)　　 som van de kwadraten
\(\sigma {\rm x}\)　　　standaardafwijking van de populatie
\({\rm sx}\)　　　 standaardafwijking steekproef
\({\rm n}\)　　　　omvang van de steekproef
\({\rm min(x)}\)　minimum
\({\rm Q}_1\)　　　eerste kwartiel
\({\rm Med}\)　　 mediaan
\({\rm Q}_3\)　　　 derde kwartiel
\({\rm max(x)}\)　maximum
\({\rm Mode}\)　　modus
\({\rm ModeN}\)　 aantal gegevens voor de modus
\({\rm ModeF}\)　frequentie van de gegevens voor de modus
Wanneer \({\rm Mode}\) meerdere oplossingen heeft, worden ze allemaal weergegeven.

Een regressiegrafiek tekenen

In dit voorbeeld gebruiken we de onderstaande gegevenswaarden om een spreidingsdiagram, een lineaire regressiegrafiek en een tweedemachts regressiegrafiek te tekenen.

1. Voer de gegevenswaarden in de onderstaande tabel in en selecteer vervolgens alle gegevens.
   

   A	B
   \(1.0\)	\(1.0\)
   \(1.2\)	\(1.1\)
   \(1.5\)	\(1.2\)
   \(1.6\)	\(1.3\)
   \(1.9\)	\(1.4\)
   \(2.1\)	\(1.5\)
   \(2.4\)	\(1.6\)
   \(2.5\)	\(1.7\)
   \(2.7\)	\(1.8\)
   \(3.0\)	\(2.0\)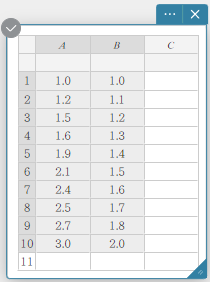

   

2. Klik op het schermtoetsenbord op [Grafiek] – [Spreidingsdiagram].
   
   Er wordt een sticky note voor een spreidingsdiagram aangemaakt en tegelijkertijd wordt er een scheidingsdiagram op de sticky note voor grafieken getekend.
   
3. Klik op het schermtoetsenbord op .
   
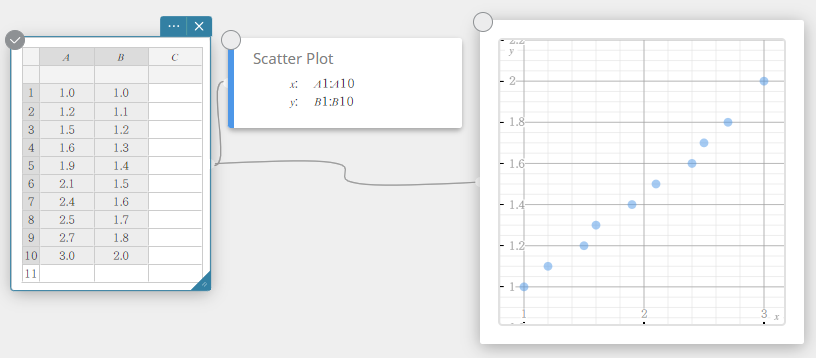
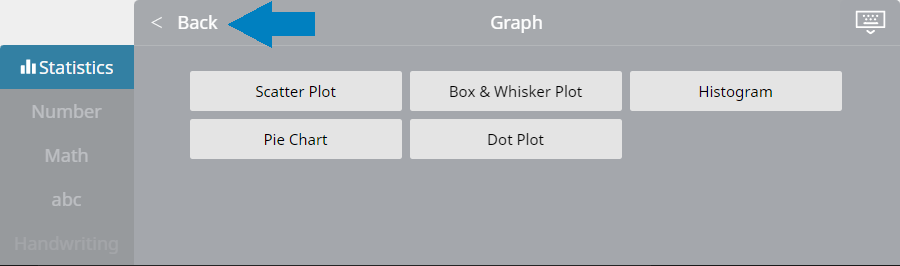
4. Klik op het schermtoetsenbord op [Regressie] – [Lineaire regressie].
   
   Er wordt een sticky note voor lineaire regressie aangemaakt en tegelijkertijd wordt er een lineaire regressiegrafiek op de sticky note voor grafieken getekend.
   
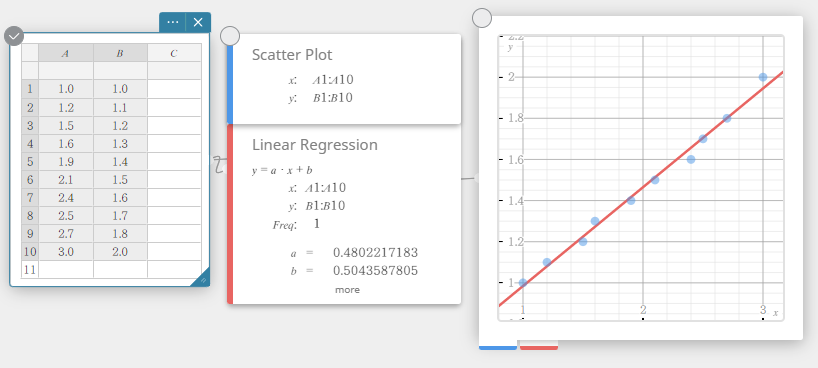
5. Klik op het schermtoetsenbord op [Tweedemachtsregressie].
   
   Er wordt een sticky note voor tweedemachtsregressie aangemaakt en tegelijkertijd wordt er een tweedemachts regressiegrafiek op de sticky note voor grafieken getekend.
   

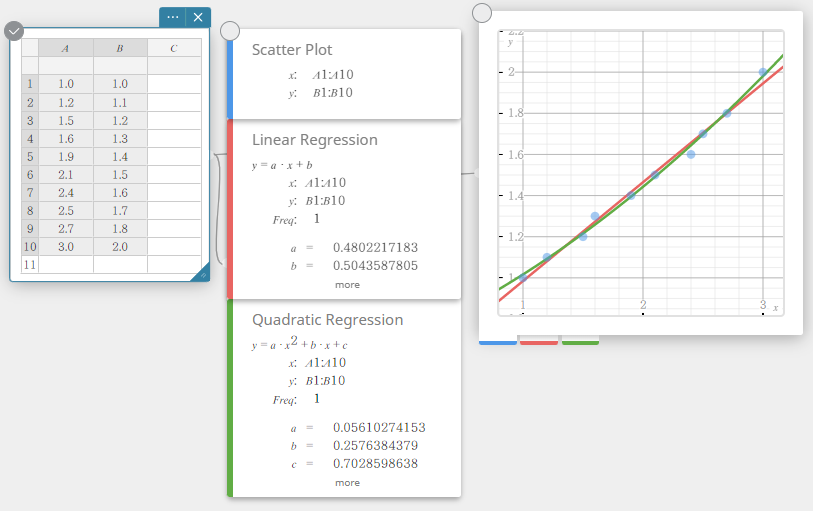
Een histogram tekenen

1. Voer de gegevenswaarden in de onderstaande tabel in, met de gegevens in kolom A en de frequentie in kolom B.
   

   Gegevens	Frequentie
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Sleep van cel A1 tot cel B5 om het celbereik ertussen te selecteren.
   

3. Klik op het schermtoetsenbord op [Grafiek] – [Histogram].
   Er wordt een sticky note voor histogram aangemaakt en tegelijkertijd wordt er een histogram op de sticky note voor grafieken getekend.
   
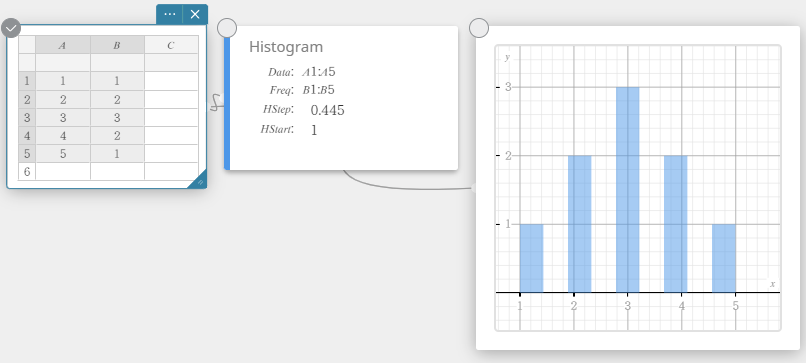
   OPMERKING
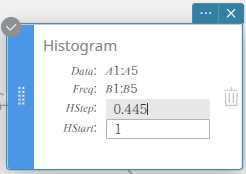
   U kunt de startwaarde (H-Start) en stapwaarde (H-Stap) van het histogram wijzigen. Klik op de sticky note voor histogram op H-Start of H-Stap en voer vervolgens de gewenste waarde in.
   

Een box-en-whiskerdiagram tekenen

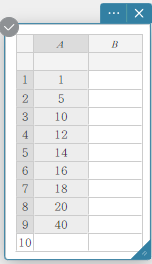
1. Voer de gegevenswaarden in de onderstaande tabel in kolom A in.
   

   A
   \(1\)
   \(5\)
   \(10\)
   \(12\)
   \(14\)
   \(16\)
   \(18\)
   \(20\)
   \(40\)

2. Sleep van cel A1 tot cel A9 om het celbereik ertussen te selecteren.
   

3. Klik op het schermtoetsenbord op [Grafiek] – [Box-en-Whiskerdiagram].
   Er wordt een sticky note voor box-en-whiskerdiagram aangemaakt en tegelijkertijd wordt er een box-en-whiskerdiagram op de sticky note voor grafieken getekend.
   
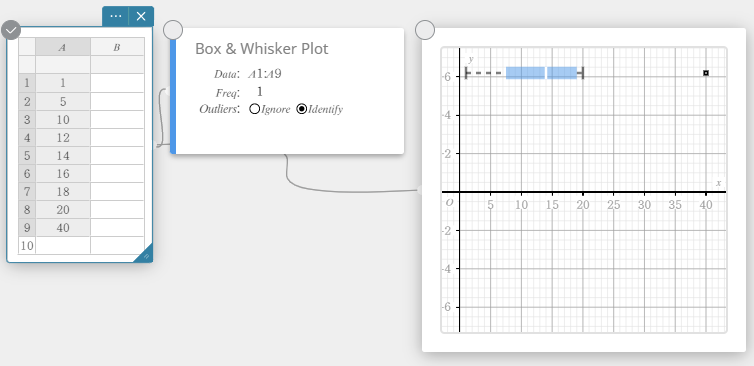
   OPMERKING
   U kunt de waarden van uitschieters weergeven. Hiertoe selecteert u [Identificeren] voor het item Uitschieters van de sticky note voor box-en-whiskerdiagram.
   

Een cirkelgrafiek tekenen

1. Voer de gegevenswaarden in de onderstaande tabel in kolom A in.
   

   A
   \(5\)
   \(10\)
   \(20\)
   \(30\)
   \(40\)

2. Sleep van cel A1 tot cel A5 om het celbereik ertussen te selecteren.
   

3. Klik op het schermtoetsenbord op [Grafiek] – [Cirkeldiagram].
   Er wordt een sticky note voor cirkeldiagram aangemaakt en tegelijkertijd wordt er een cirkeldiagram op een afzonderlijke sticky note*getekend.
   
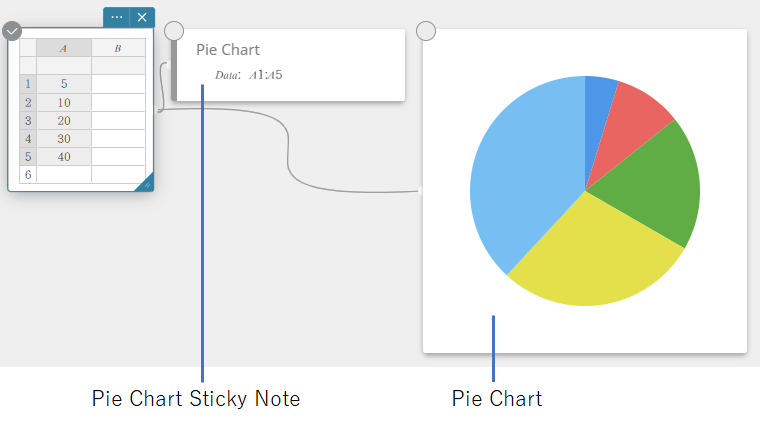
   *　De grafiek wordt getekend op de sticky note voor grafieken. Het type is anders wanneer een cirkeldiagram op de sticky note wordt getekend.

Bewerkingen van spreidingsdiagram

• De punten van een spreidingsdiagram verplaatsen

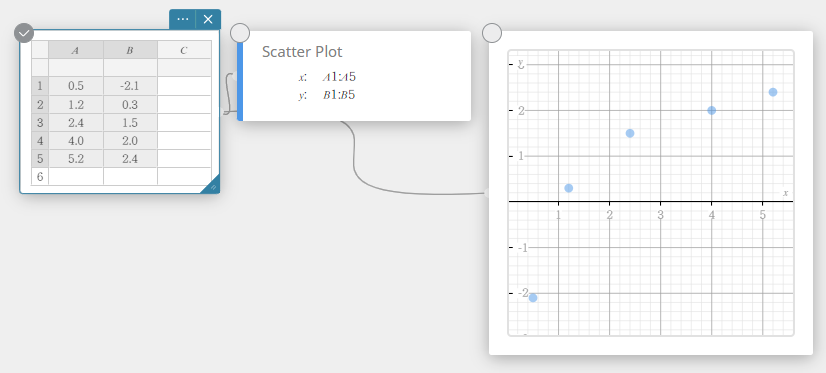
1. Voer de gegevenswaarden in de onderstaande tabel in de kolommen A en B in.
   

   Gegevens	Frequentie
   \(0.5\)	\(-2.1\)
   \(1.2\)	\(0.3\)
   \(2.4\)	\(1.5\)
   \(4.0\)	\(2.0\)
   \(5.2\)	\(2.4\)

2. Sleep van cel A1 tot cel B5 om het celbereik ertussen te selecteren.
   

3. Klik op het schermtoetsenbord op [Grafiek] – [Spreidingsdiagram].
   Er wordt een sticky note voor spreidingsdiagram en een sticky note voor grafieken aangemaakt, en er wordt een scheidingsdiagram op de sticky note voor grafieken getekend.
   
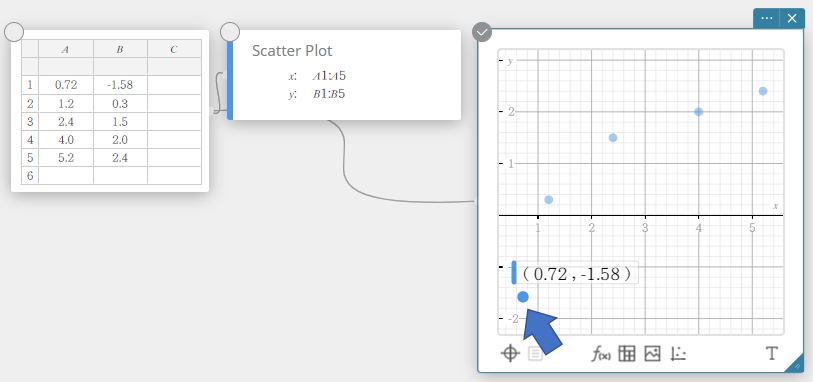
4. Om een punt van een spreidingsdiagram te verplaatsen, sleept u het.
   Dit wijzigt ook de waarden van de sticky note voor statistische gegevens naar de coördinaten van de bestemming.
   

• Een cel vergrendelen

OPMERKING
Wanneer een cel is vergrendeld, wijzigt de gegevenswaarde ervan niet, zelfs als u het punt van het spreidingsdiagram probeert te verplaatsen. Als u bijvoorbeeld een cel in kolom A vergrendelt, kan het bijbehorende punt van het spreidingsdiagram niet langs de x-as worden verplaatst.

1. Na de procedure onder “De punten van een spreidingsdiagram verplaatsen“ selecteert u cel A1.
2. Klik op op de sticky note voor statistische berekeningen.
   
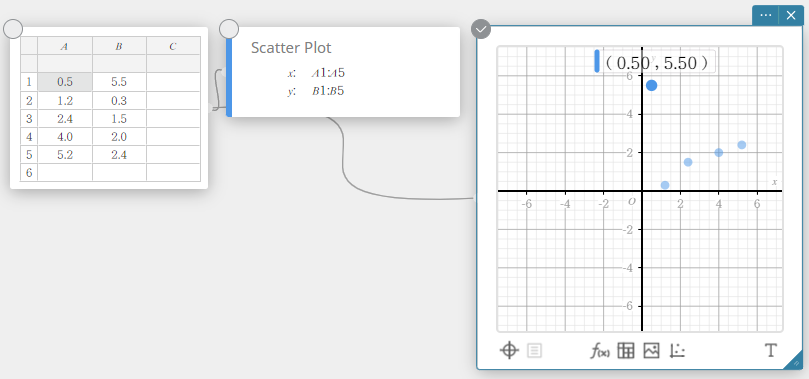
3. Klik op het pictogram naast [Vergrendelen].
   De cel A1 wordt vergrendeld. Als u het punt van het spreidingsdiagram dat overeenkomt met de cellen A1 en B1 sleept, is er geen beweging mogelijk langs de x-as.
   

• Een cel ontgrendelen

1. Selecteer de vergrendelde cel die u wilt ontgrendelen.
2. Klik op op de sticky note voor statistische berekeningen.
   
3. Klik op het pictogram naast [Ontgrendelen].

Een Z-test van één steekproef uitvoeren

• Hiermee bepaalt u het aantal gegevensstalen en voert u vervolgens een Z-test van één steekproef uit

Voorbeeld:
Omvang van de steekproef: \(n=48\)
Steekproefgemiddelde: \(\overline{x}=24.5\)
Nulhypothese: \(\mu \ne 0\)
Standaardafwijking: \(\sigma=3\)

1. Maak een sticky note voor statistische gegevens aan.
2. Klik op het schermtoetsenbord op [Test] – [Z-test van één steekproef].
   
   Er wordt een sticky note voor Z-test van één steekproef aangemaakt.
   
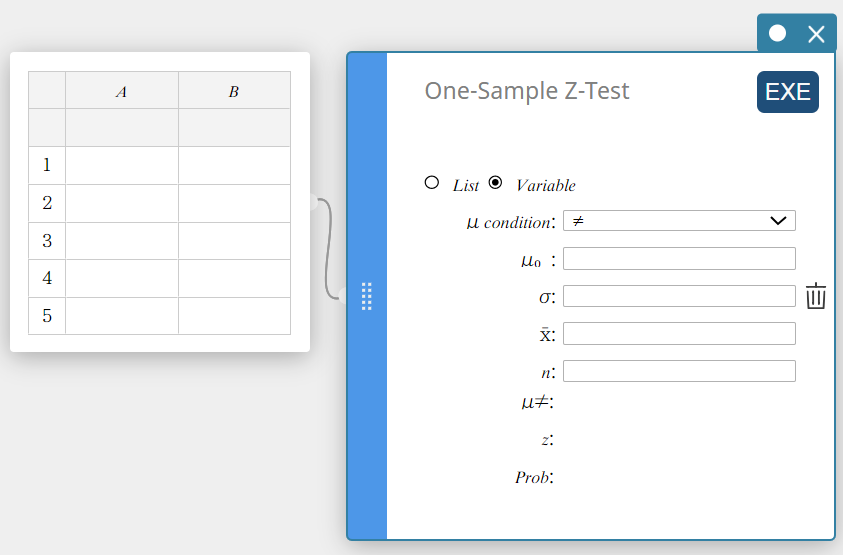
3. Configureer de instellingen zoals hieronder getoond.
   \(\mu\) voorwaarde: Selecteer “\(\ne\)” in het menu dat verschijnt.
   \(\mu_0\) : Voer in \(0\).
   \(\sigma\): Voer in \(3\).
   \(\overline{x}\) : Voer in \(24.5\).
   \(n\) : Voer in \(48\).
   
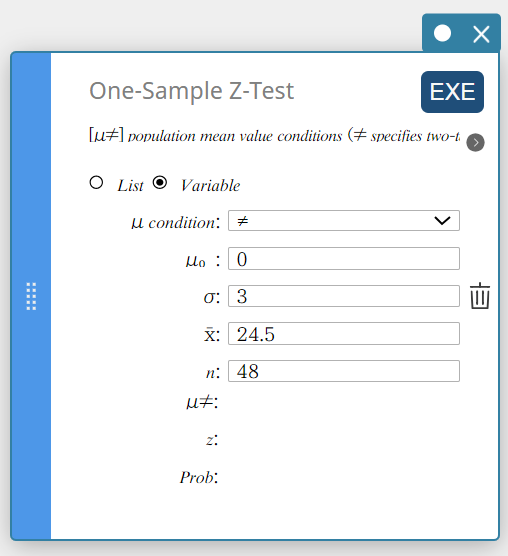
4. Klik op [EXE].
   
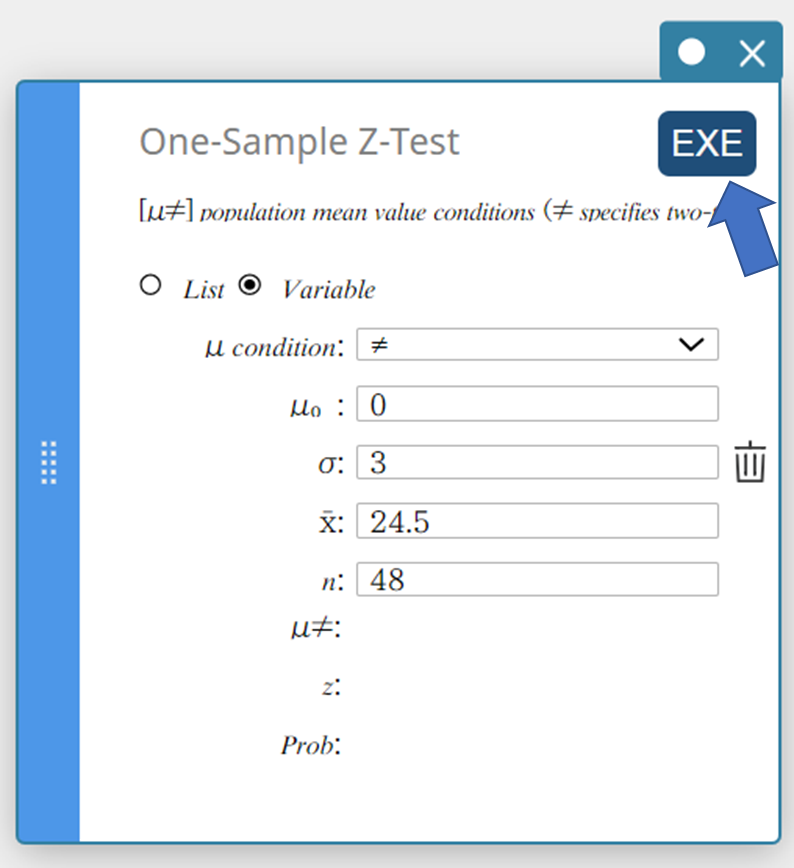
   Hiermee worden de berekeningsresultaten en de grafiek weergegeven.
   
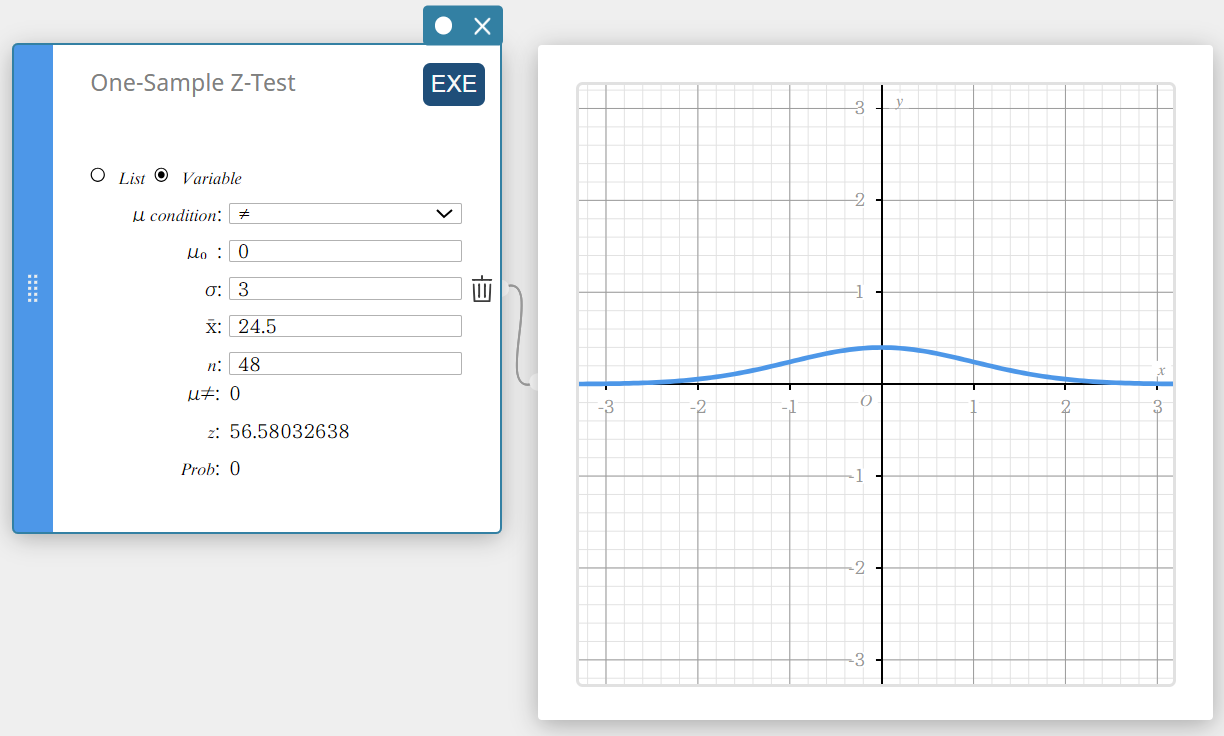
   \(\mu \ne\) voorwaarde voor de gemiddelde waarde van de populatie
   \(\rm z\) 　　\(\rm z\)-waarde
   Prob 　\(\rm p\)-waarde
   \(\overline{x}\) 　　steekproefgemiddelde
   \(n\) 　　omvang van de steekproef

• Gebruik van lijsten om een Z-test van één steekproef uit te voeren

1. Voer de volgende lijstnamen in: Lijst 1 voor kolom A, Lijst 2 voor kolom B.
2. Voer de gegevenswaarde in onderstaande tabel in.
   
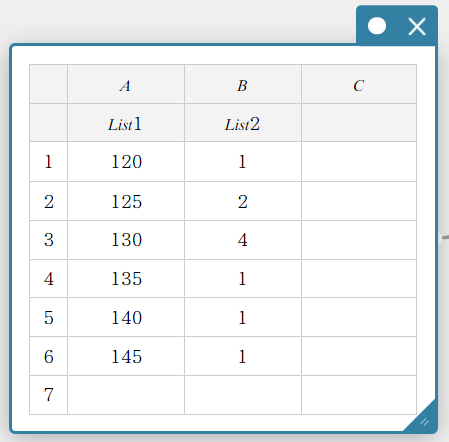
3. Sleep van cel A1 tot cel B6 om het celbereik te selecteren.
4. Klik op het schermtoetsenbord op [Test] – [Z-test van één steekproef].
   
   Er wordt een sticky note voor Z-test van één steekproef aangemaakt.
   
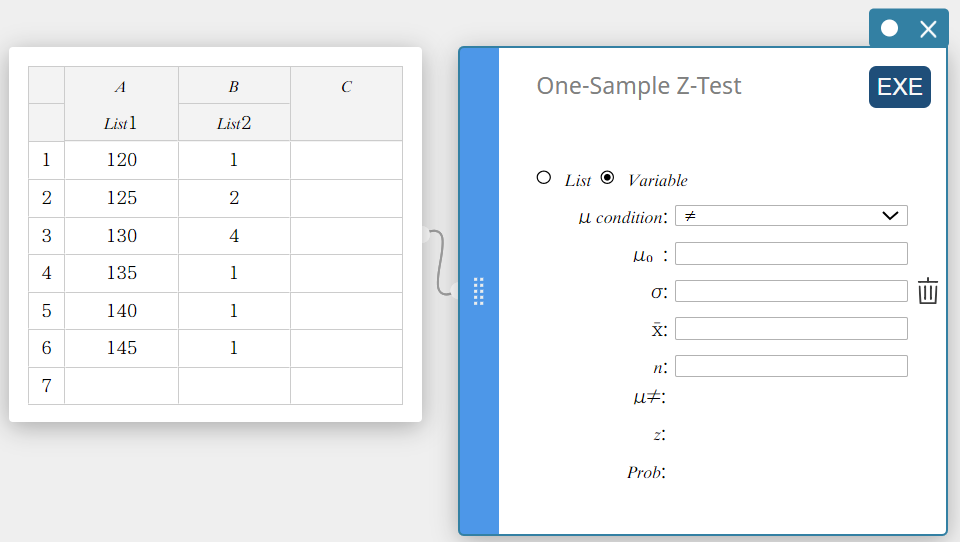
5. Klik op “List”.
   
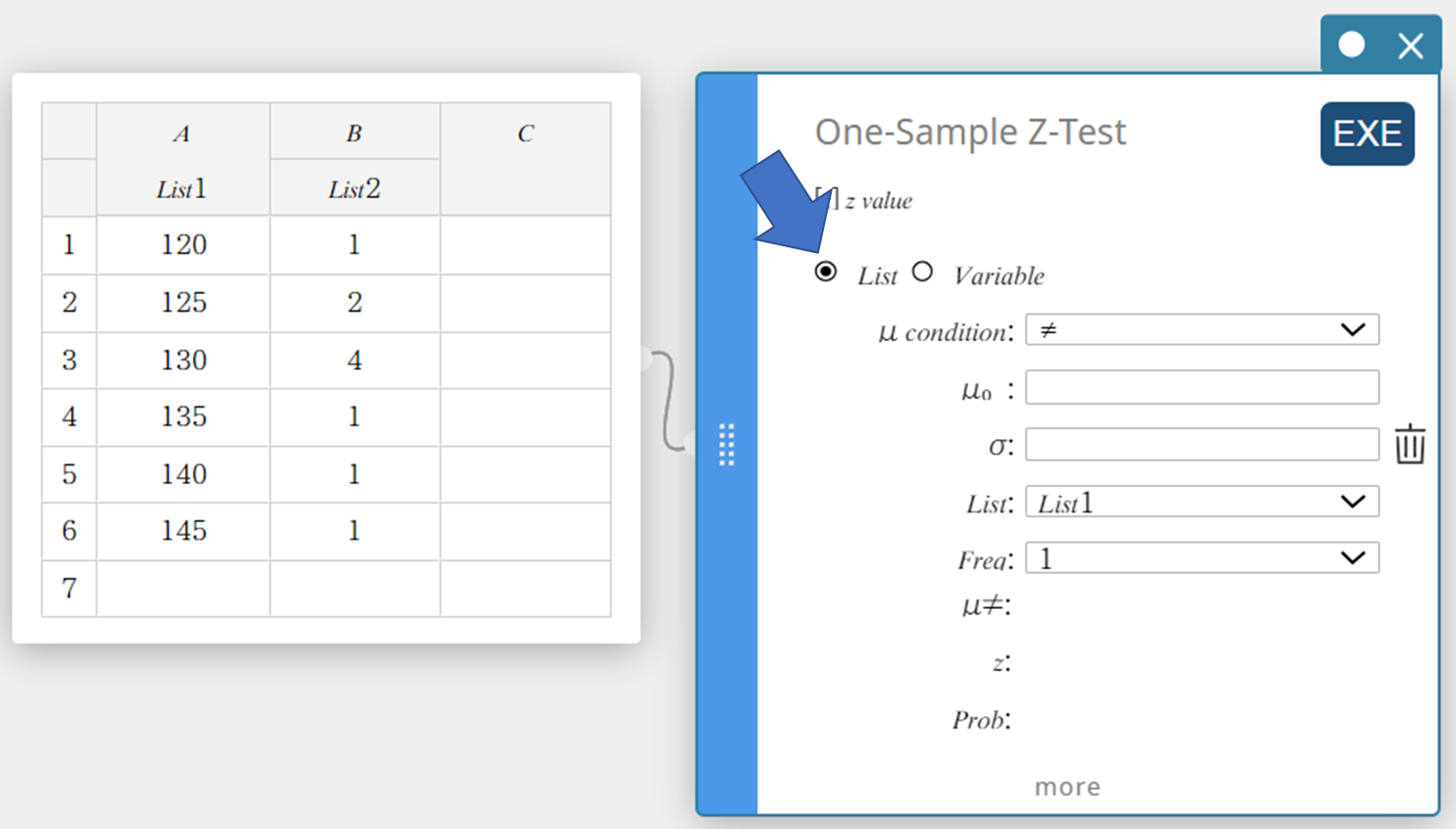
6. Configureer de instellingen zoals hieronder getoond.
   \(\mu\) voorwaarde: Selecteer “\(\gt\)” in het menu dat verschijnt.
   \(\mu_0\) : Voer in \(120\).
   \(\sigma\): Voer in \(19\).
   List: Selecteer “List1” in het menu dat verschijnt.
   Freq: Selecteer “List2” in het menu dat verschijnt.
   
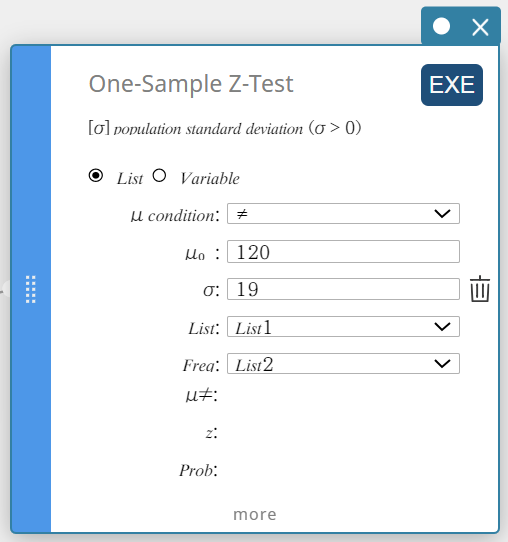
7. Klik op [EXE].
   
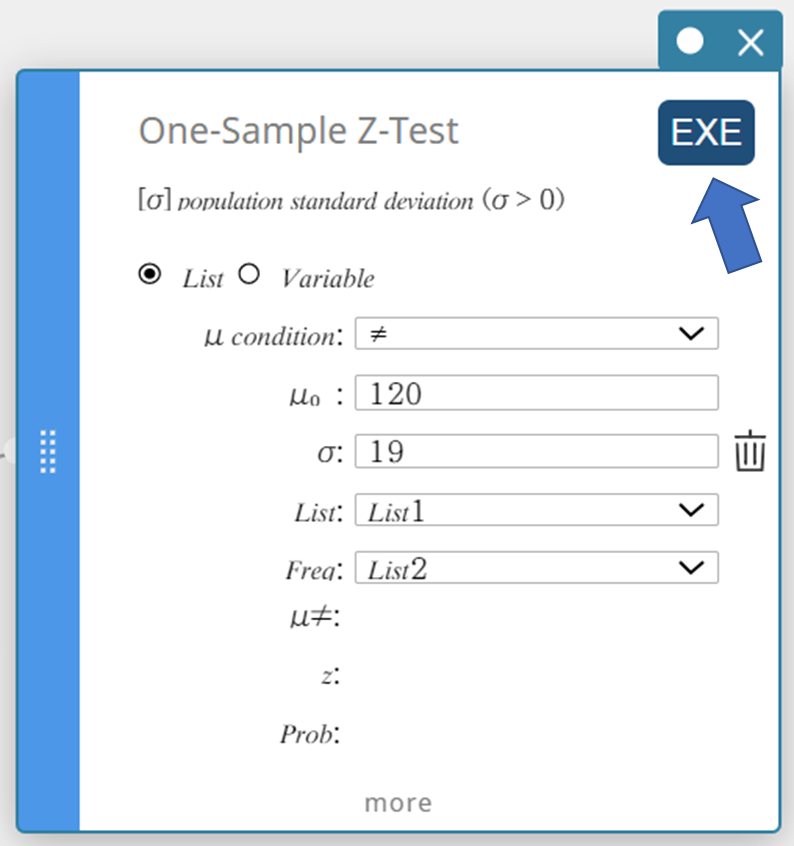
   Hiermee worden de berekeningsresultaten en de grafiek weergegeven.
   
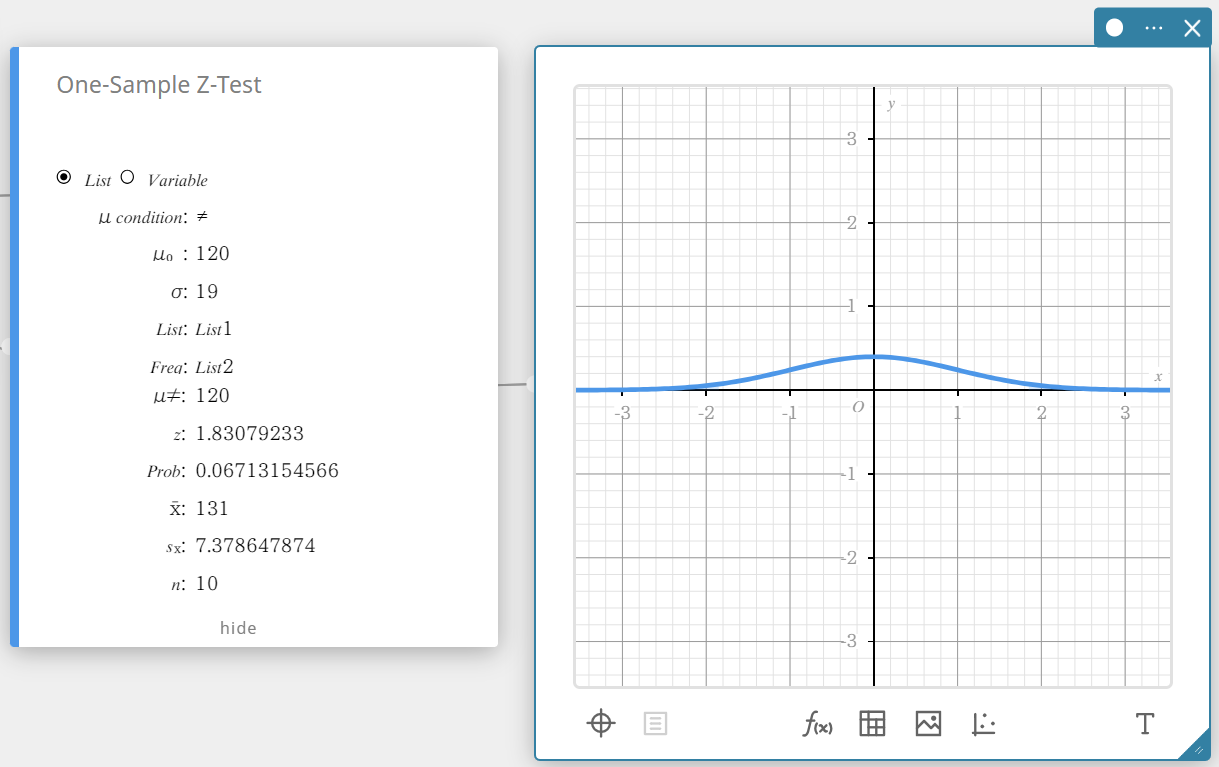
   \(\mu \gt\)　voorwaarde voor de gemiddelde waarde van de populatie
   \(\rm z\)　　　\(\rm z\)-waarde
   Prob　　\(\rm p\)-waarde
   \(\overline{x}\)　　　steekproefgemiddelde
   \({\rm Sx}\)　　standaardafwijking steekproef
   \(n\)　　　omvang van de steekproef

Statistische berekeningen en grafieken

Statistische berekeningen

Eén-variabele
Hiermee worden de berekeningsresultaten van statistieken met één variabele weergegeven.

\(\bar{\rm x}\) … steekproefgemiddelde
\(\Sigma {\rm x}\) … som van de gegevens
\(\Sigma {\rm x}^2\) … som van de kwadraten
\(\sigma {\rm x}\) … standaardafwijking van de populatie
\({\rm sx}\) … standaardafwijking van de steekproef
\({\rm n}\) … omvang van de steekproef
\({\rm min(x)}\) … minimum
\({\rm Q}_1\) … eerste kwartiel
\({\rm Med}\) … mediaan
\({\rm Q}_3\) … derde kwartiel
\({\rm max(x)}\) … maximum
\({\rm Mode}\) … modus
\({\rm ModeN}\) … aantal gegevens voor de modus
\({\rm ModeF}\) … frequentie van de gegevens voor de modus

Wanneer \({\rm Mode}\) meerdere oplossingen heeft, worden ze allemaal weergegeven.

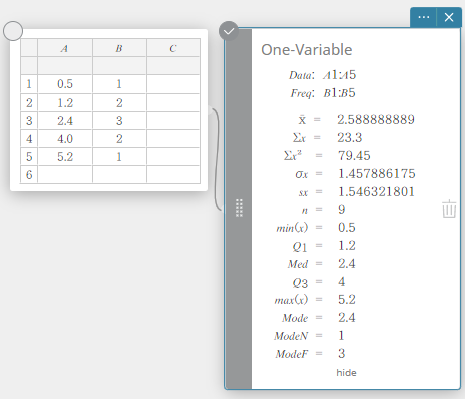
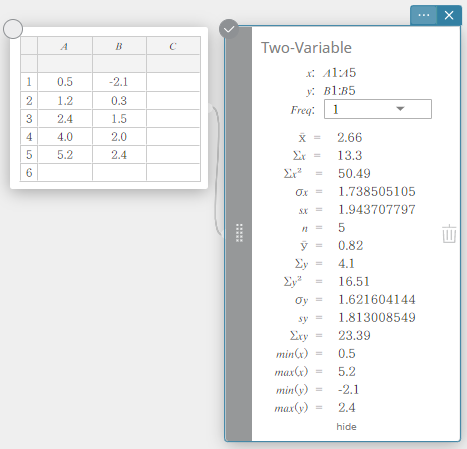
Twee-variabele
Hiermee worden de berekeningsresultaten van statistieken met gecombineerde variabelen weergegeven.

\(\bar{\rm x}\) … steekproefgemiddelde
\(\Sigma {\rm x}\) … som van de gegevens
\(\Sigma {\rm x}^2\) … som van de kwadraten
\(\sigma {\rm x}\) … standaardafwijking van de populatie
\({\rm sx}\) … standaardafwijking van de steekproef
\({\rm n}\) … omvang van de steekproef
\(\bar{\rm y}\) … steekproefgemiddelde
\(\Sigma {\rm y}\) … som van de gegevens
\(\Sigma {\rm y}^2\) … som van de kwadraten
\(\sigma {\rm y}\) … standaardafwijking van de populatie
\({\rm sy}\) … standaardafwijking steekproef
\(\Sigma {\rm xy}\) … som van de producten XList- en YList-gegevens
\({\rm minX}\) … minimum
\({\rm maxX}\) … maximum
\({\rm minY}\)… minimum
\({\rm maxY}\) … maximum

Regressieberekeningen en grafieken

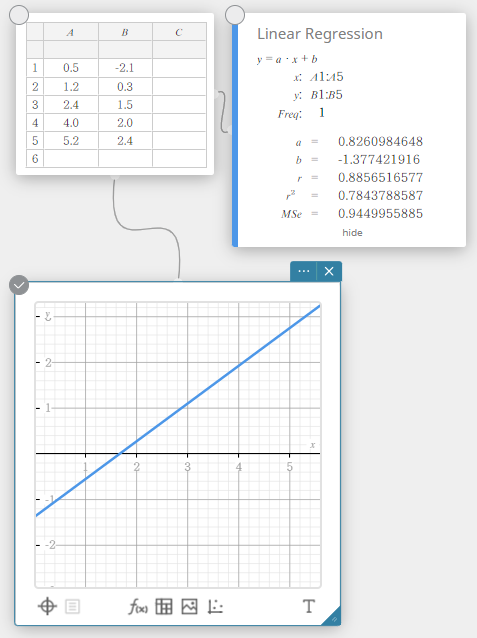
Lineaire regressie
Lineaire regressie gebruikt de kleinste kwadraten-methode om de vergelijking te vinden die het beste overeenstemt met uw gegevenspunten, en geeft waarden voor de helling en het y-snijpunt. De grafische weergave van deze relatie is een lineaire regressiegrafiek.

\(y = a \cdot x + b\)
\(a\) … regressiecoëfficiënt (helling)
\(b\) … regressieconstante (y-snijpunt)
\(r\) … correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

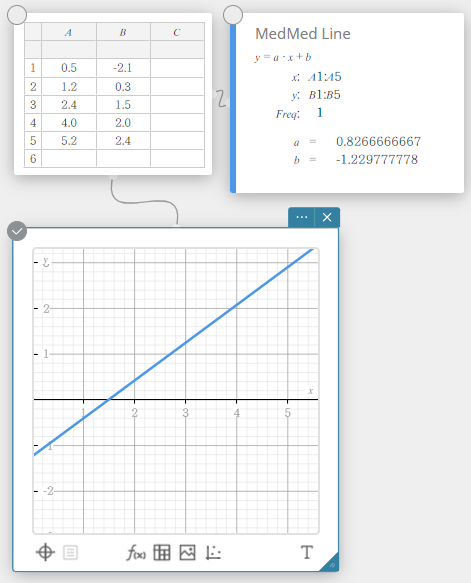
Med-Med-regressie
Wanneer u vermoedt dat de gegevens extreme waarden bevatten, moet u de Med-Med-grafiek gebruiken (die op medianen is gebaseerd) in plaats van de lineaire regressiegrafiek. De Med-Med-grafiek is vergelijkbaar met de lineaire regressiegrafiek maar minimaliseert ook de effecten van extreme waarden.

\(y = a \cdot x + b\)
\(a\) … regressiecoëfficiënt (helling)
\(b\) … regressieconstante (y-snijpunt)

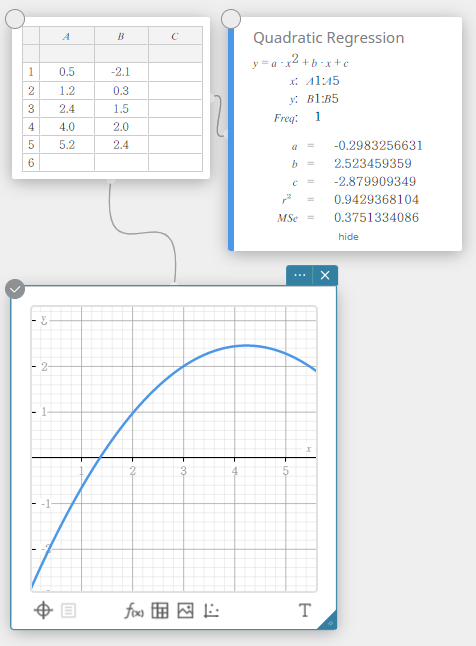
Tweedemachtsregressie
De tweedemachts regressiegrafiek gebruikt de methode van de kleinste kwadraten om een kromme te tekenen die de omgeving van zoveel mogelijk beeldpunten benadert. Deze grafiek kan worden uitgedrukt als een uitdrukking van een tweedemachtsregressie.

\(y = a \cdot x^2 + b \cdot x + c\)
\(a\) … regressie tweede coëfficiënt
\(b\) … regressie eerste coëfficiënt
\(c\) … regressieconstante (y-snijpunt)
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

Derdemachtsregressie
De derdemachts regressiegrafiek gebruikt de methode van de kleinste kwadraten om een kromme te tekenen die de omgeving van zoveel mogelijk beeldpunten benadert. Deze grafiek kan worden uitgedrukt als een uitdrukking van een derdemachtsregressie.

\(y = a \cdot x^3 + b \cdot x^2 + c \cdot x + d\)
\(a\) … regressie derde coëfficiënt
\(b\) … regressie tweede coëfficiënt
\(c\) … regressie eerste coëfficiënt
\(d\) … regressieconstante (y-snijpunt)
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

Vierdemachtsregressie
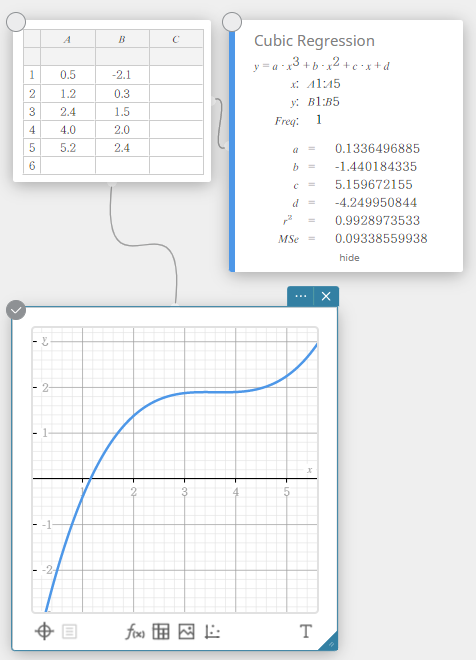
De vierdemachts regressiegrafiek gebruikt de methode van de kleinste kwadraten om een kromme te tekenen die de omgeving van zoveel mogelijk beeldpunten benadert. Deze grafiek kan worden uitgedrukt als een uitdrukking van een vierdemachtsregressie.

\(y = a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e\)
\(a\) … regressie vierde coëfficiënt
\(b\) … regressie derde coëfficiënt
\(c\) … regressie tweede coëfficiënt
\(d\) … regressie eerste coëfficiënt
\(e\) … regressieconstante (y-snijpunt)
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

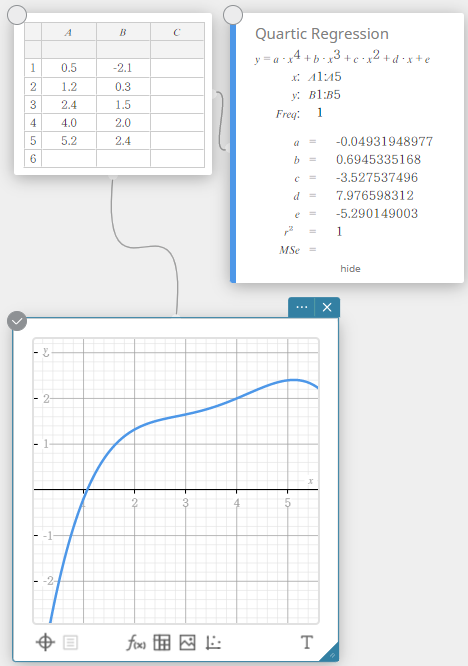
Logaritmische regressie
De logaritmische regressie drukt \(y\) uit als een logaritmische functie van \(x\). De normale formule voor logaritmische regressie is \(y=a+b \cdot \ln(x)\). Als we zeggen dat \(X=\ln(x)\), dan komt deze formule overeen met de formule voor lineaire regressie \(y=a+b \cdot X\).

\(y = a + b \cdot \ln(x)\)
\(a\) … regressieconstante
\(b\) … regressiecoëfficiënt
\(r\) … correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

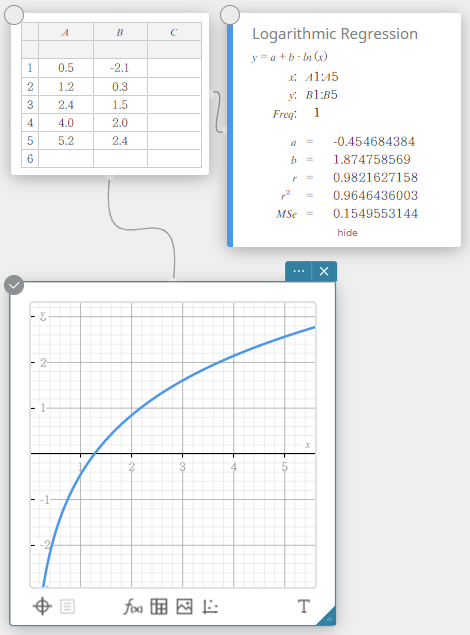
Exponentiële regressie
Exponentiële regressie kan worden gebruikt wanneer \(y\) evenredig is met de exponentiële functie van \(x\). De normale formule voor exponentiële regressie is \(y=a \cdot e^{b \cdot x}\). Als we de logaritmen van beide kanten verkrijgen, krijgen we \(\ln(y)=\ln(a)+b \cdot x\). Als we vervolgens zeggen dat \(Y=\ln(y)\) en \(A=\ln(a)\), dan komt de formule overeen met de formule voor lineaire regressie \(Y=A+b \cdot x\).

\(y = a \cdot e^{b \cdot x}\)
\(a\) … regressiecoëfficiënt
\(b\) … regressieconstante
\(r\) … correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

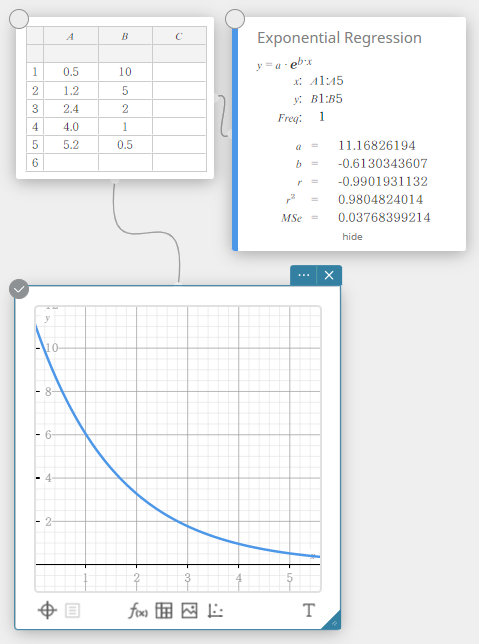
abExponentiële regressie
Exponentiële regressie kan worden gebruikt wanneer \(y\) evenredig is met de exponentiële functie van \(x\). De normale formule voor exponentiële regressie is \(y=a \cdot b^x\). Als we de natuurlijke logaritmen van beide kanten nemen, krijgen we \(\ln(y)=\ln(a)+(\ln(b)) \cdot x\). Als we vervolgens zeggen dat \(Y=\ln(y)\), \(A=\ln(a)\) en \(B=\ln(b)\), dan komt de formule overeen met de formule voor lineaire regressie \(Y=A+B \cdot x\).

\(y = a \cdot b^x\)
\(a\) … regressieconstante
\(b\) … regressiecoëfficiënt
\(r\) … correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

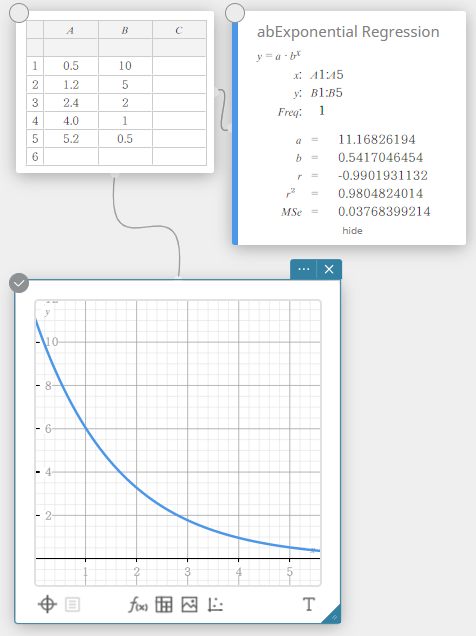
Inverse regressie
De omgekeerde regressie drukt \(y\) uit als een omgekeerde functie van \(x\). De normale formule voor omgekeerde regressie is \(y=a+b/x\). Als we zeggen dat \(X=1/x\), dan komt deze formule overeen met de formule voor lineaire regressie \(y=a+b･X\).

\(y=a+b/x\)
\(a\) … regressieconstante
\(b\) … regressiecoëfficiënt
\(r\) …. correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

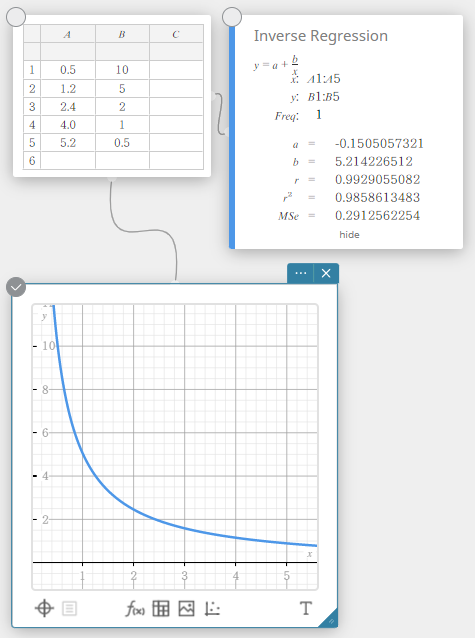
Machtsregressie
Machtsregressie kan worden gebruikt wanneer \(y\) evenredig is met de macht van \(x\). De normale formule voor machtsregressie is \(y=a \cdot x^b\). Als we de natuurlijke logaritmen van beide kanten verkrijgen, krijgen we \(\ln(y)=\ln(a)+b \cdot \ln(x)\). Als we vervolgens zeggen dat \(X=\ln(x)\), \(Y=\ln(y)\), en \(A=\ln(a)\), dan komt de formule overeen met de formule voor lineaire regressie \(Y=A+b \cdot X\).

\(y = a \cdot x^b\)
\(a\) … regressiecoëfficiënt
\(b\) … regressiemacht
\(r\) … correlatiecoëfficiënt
\(r^2\) … determinatiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

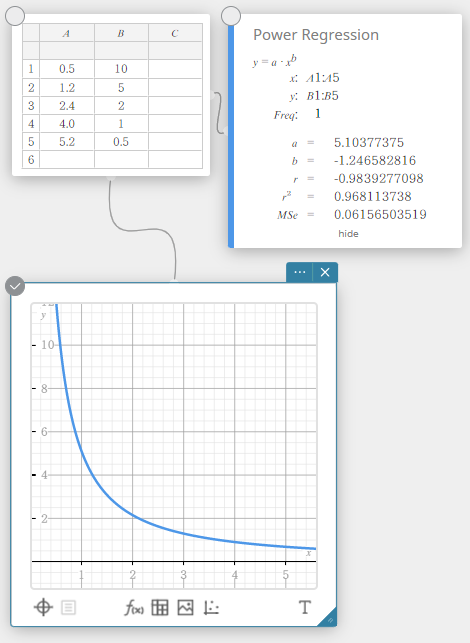
Sinusvormige regressie
Sinusvormige regressie is het best voor gegevens die zich op regelmatige vaste tijdstippen herhalen.

\(y = a \cdot \sin( b \cdot x + c ) + d\)
\(a\), \(b\), \(c\), \(d\) … regressiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

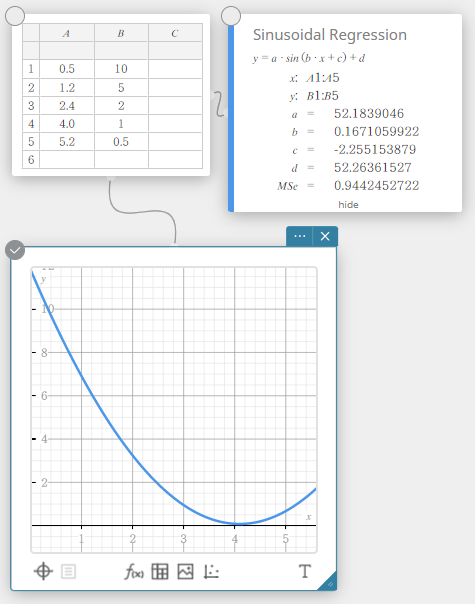
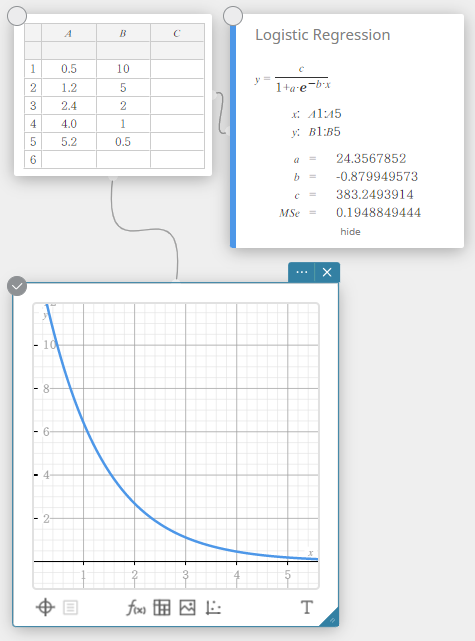
Logistieke regressie
Logistieke regressie is het best voor gegevens waarvan de waarden onophoudelijk stijgen tot een verzadigingspunt is bereikt.

\(\displaystyle y=\frac{c}{1+a \cdot e^{-b \cdot x}}\)
\(a\), \(b\), \(c\) … regressiecoëfficiënt
\({\rm MSe}\) … gemiddelde kwadraten van de fouten

Tests

Z-Test van één steekproef
Hiermee wordt één steekproefgemiddelde getest tegenover het bekende gemiddelde van de nulhypothese wanneer de standaardafwijking van de populatie bekend is. De normale verdeling wordt gebruikt voor de Z-test van één steekproef.

\(Z=\displaystyle \frac{\overline{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) : steekproefgemiddelde
\(\mu_{0}\) : aangenomen gemiddelde populatie
\(\sigma\) : standaardafwijking van de populatie
\(n\) : grootte van de steekproef

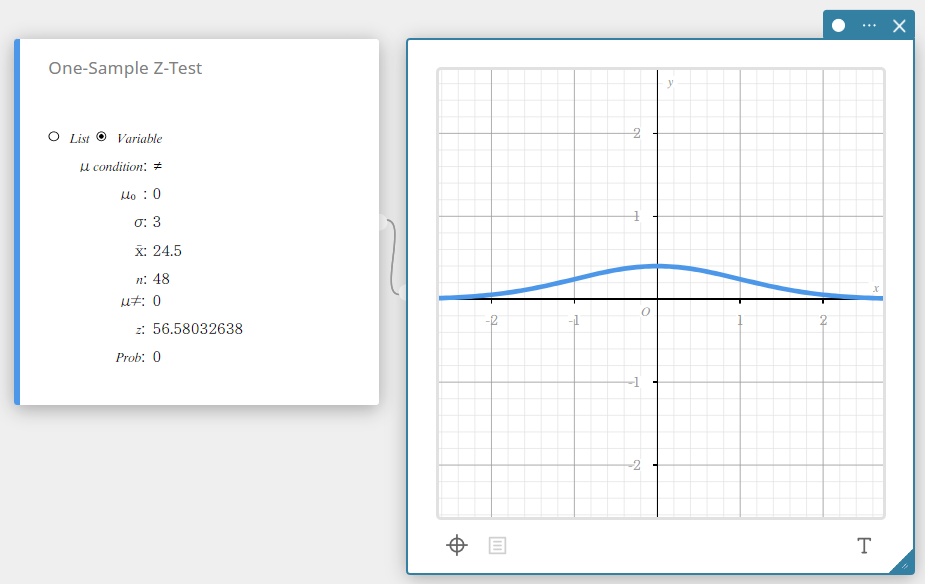
Gegevenstype: Variabele

• Invoertermen
  \( \mu \) condition : testvoorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  \( \mu_{0} \) : aangenomen gemiddelde populatie
  \( \sigma \) : standaardafwijking van de populatie（\( \sigma > 0 \)）
  \(\overline{x}\) : steekproefgemiddelde
  \(n\) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  \( \mu \neq \) : voorwaarde voor de gemiddelde waarde van de populatie
  \(z\) : z-waarde
  Prob : \(p\)-waarde

Gegevenstype: Lijst

• Invoertermen
  \( \mu \) condition : testvoorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  \( \mu_{0} \) : aangenomen gemiddelde populatie
  \( \sigma \) : standaardafwijking van de populatie （\( \sigma > 0 \)）
  List : gegevenslijst
  Freq : frequentie (1 of lijstnaam)

• Uitvoertermen
  \( \mu \neq \) : voorwaarde voor de gemiddelde waarde van de populatie
  \(z\) : \(z\)-waarde
  Prob : \(p\)-waarde
  \( \overline{x} \) : steekproefgemiddelde
  \( s_{x} \) : standaardafwijking steekproef
  \( n \) : grootte van de steekproef

Z-test van twee steekproeven
Dit test het verschil tussen twee gemiddelden wanneer de standaardafwijkingen van de twee populaties bekend zijn. De normale verdeling wordt gebruikt voor de Z-test van twee steekproeven.

\( Z=\displaystyle \frac{ \overline{x}_{1} – \overline{x}_{2} }{ \sqrt{\displaystyle \frac{{\sigma_{1}}^2}{n_{1}} +\displaystyle \frac{{\sigma_{2}}^2}{n_{2}} } } \)

\( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
\( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
\( \sigma_{1} \) : standaardafwijking van de populatie van steekproef 1
\( \sigma_{2} \) : standaardafwijking van de populatie van steekproef 2
\( n_{1} \) : grootte van steekproef 1
\( n_{2} \) : grootte van steekproef 2

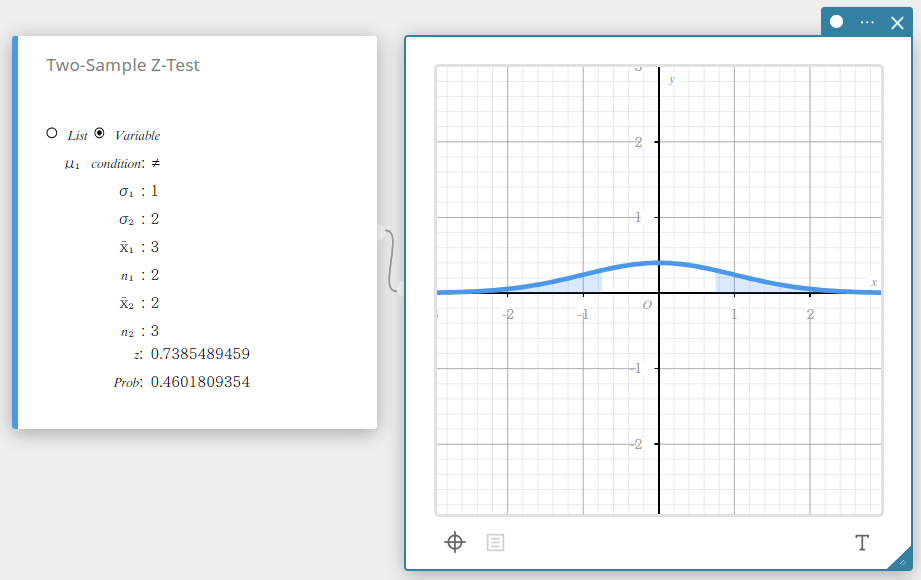
Gegevenstype: Variabele

• Invoertermen
  \( \mu_{1} \) voorwaarde : voorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 minder is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2).
  \( \sigma_{1} \) : standaardafwijking van de populatie van steekproef 1 （\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : standaardafwijking van de populatie van steekproef 2（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( n_{1} \) : grootte van steekproef 1 (positief geheel getal)
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( n_{2} \) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  \(z\) : z-waarde
  Prob : \(p\)-waarde

Gegevenstype: Lijst

• Invoertermen
  \( \mu_{1} \) voorwaarde : voorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 minder is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2).
  \( \sigma_{1} \) : standaardafwijking van de populatie van steekproef 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : standaardafwijking van de populatie van steekproef 2（\( \sigma_{2} > 0 \)）
  List(1) : lijst met gegevens van steekproef 1
  List(2) : lijst met gegevens van steekproef 2
  Freq(1) : steekproeffrequentie 1 (1 of lijstnaam)
  Freq(2) : steekproeffrequentie 2 (1 of lijstnaam)

• Uitvoertermen
  \(z\) : z-waarde
  Prob : \(p\)-waarde
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( s_{x_{1}} \) : standaardafwijking van steekproef 1
  \( s_{x_{2}} \) : standaardafwijking van steekproef 2
  \( n_{1} \) : grootte van steekproef 1
  \( n_{2} \) : grootte van steekproef 2

Z-Test van één voorwerp (Z-Test van één voorwerp)
Hiermee wordt één steekproefproportie getest tegenover de bekende proportie van de nulhypothese. De normale verdeling wordt gebruikt voor de Z-test van één proportie.

\(Z =\displaystyle \frac{\displaystyle \frac{x}{n} – p_{0} }{ \sqrt{\displaystyle \frac{ p_{0}(1-p_{0}) }{n} }}\)
\(p_{0}\) : verwacht gedeelte van de steekproef
\(n\) : grootte van de steekproef

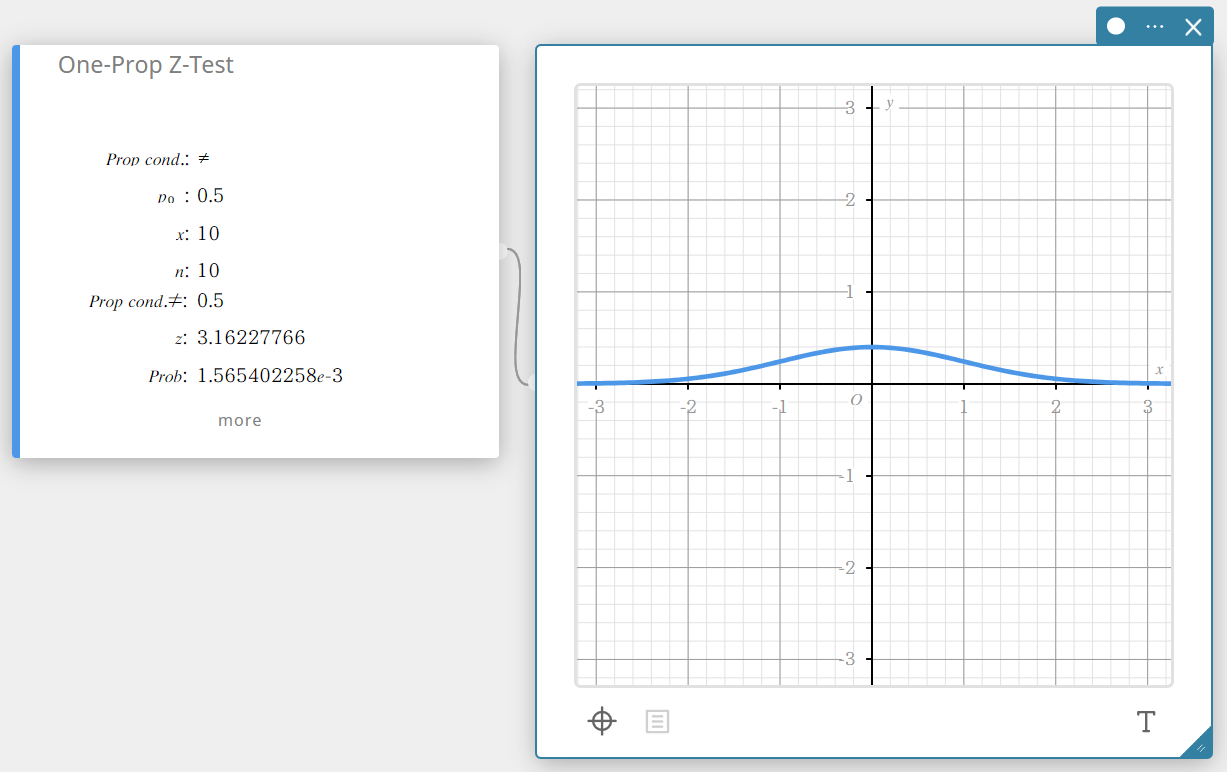
• Invoertermen
  Prop cond : testvoorwaarde voor gedeelte van steekproef (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  \(p_{0}\) : verwachte proportie van de steekproef（\( 0 < p_{0} < 1 \)）
  \(x\) : waarde van de steekproef (geheel getal, \( x \geq 0 \)）
  \(n\) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  Prop Cond \(\neq\) : testvoorwaarde van gedeelte van de steekproef
  \(z\) : z-waarde
  Prob : \(p\)-waarde
  \(\hat{p}\) : verwacht gedeelte van steekproef

Z-Test van twee voorwerpen (Z-Test van twee voorwerpen)
Hiermee wordt het verschil getest tussen twee proporties van de steekproef. De normale verdeling wordt gebruikt voor de Z-test van twee proporties.

\( Z =\displaystyle \frac{\displaystyle \frac{x_{1}}{n_{1}} -\displaystyle \frac{x_{2}}{n_{2}} }{ \sqrt{ \hat{p} \left(1-\hat{p} \right) \left(\displaystyle \frac{1}{n_{1}} +\displaystyle \frac{1}{n_{2}} \right) } }\)
\(x_{1}\) : gegevenswaarde van steekproef 1
\(x_{2}\) : gegevenswaarde van steekproef 2
\(n_{1}\) : grootte van steekproef 1
\(n_{2}\) : grootte van steekproef 2
\(\hat{p}\) : verwacht gedeelte van steekproef

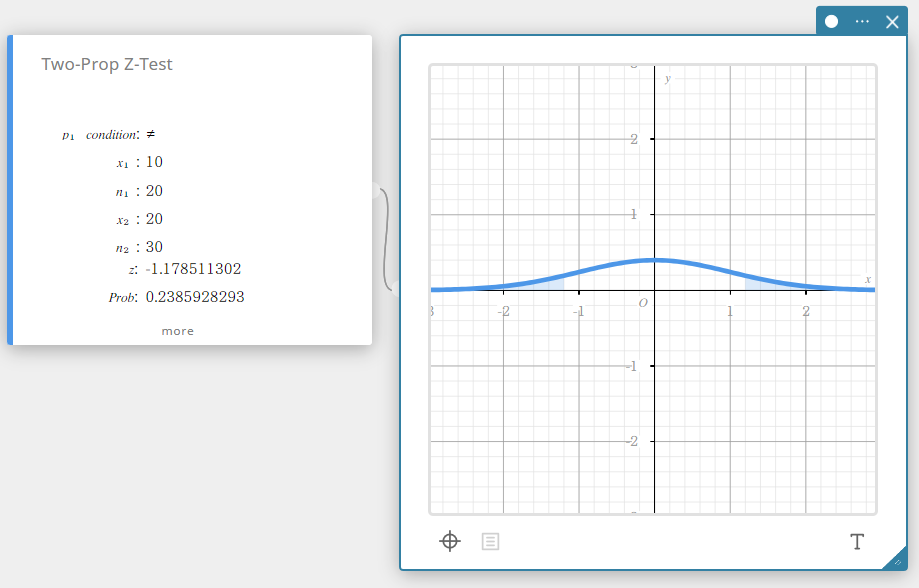
• Invoertermen
  \(p_{1}\) condition : testvoorwaarden voor gedeelte van steekproef (“\(\neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 kleiner is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2.)
  \(x_{1}\) : gegevenswaarde van steekproef 1 (geheel getal, \(x_{1}\) moet kleiner of gelijk zijn aan \(n_{1}\))
  \(n_{1}\) : grootte van steekproef 1 (positief geheel getal)
  \(x_{2}\) : gegevenswaarde van steekproef 2 (geheel getal, \(x_{2}\) moet kleiner of gelijk zijn aan \(n_{2}\))
  \(n_{2}\) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  \(z\) : z-waarde
  Prob : \(p\)-waarde
  \(\hat{p}_{1}\) : verwacht gedeelte van steekproef 1
  \(\hat{p}_{2}\) : verwacht gedeelte van steekproef 2
  \(\hat{p}\) : verwacht gedeelte van steekproef

\(t\)-test van één steekproef
Hiermee wordt één steekproefgemiddelde getest tegenover het bekende gemiddelde van de nulhypothese wanneer de standaardafwijking van de populatie onbekend is. De \(t\)-verdeling wordt gebruikt voor de \(t\)-test van één steekproef.

\(t =\displaystyle \frac{ \overline{x} – \mu_{0} }{\displaystyle \frac{ s_{x} }{ \sqrt{n} } }\)
\(\overline{x}\) : steekproefgemiddelde
\(\mu_{0}\) : aangenomen gemiddelde populatie
\(s_{x}\) : standaardafwijking steekproef
\(n\) : grootte van de steekproef

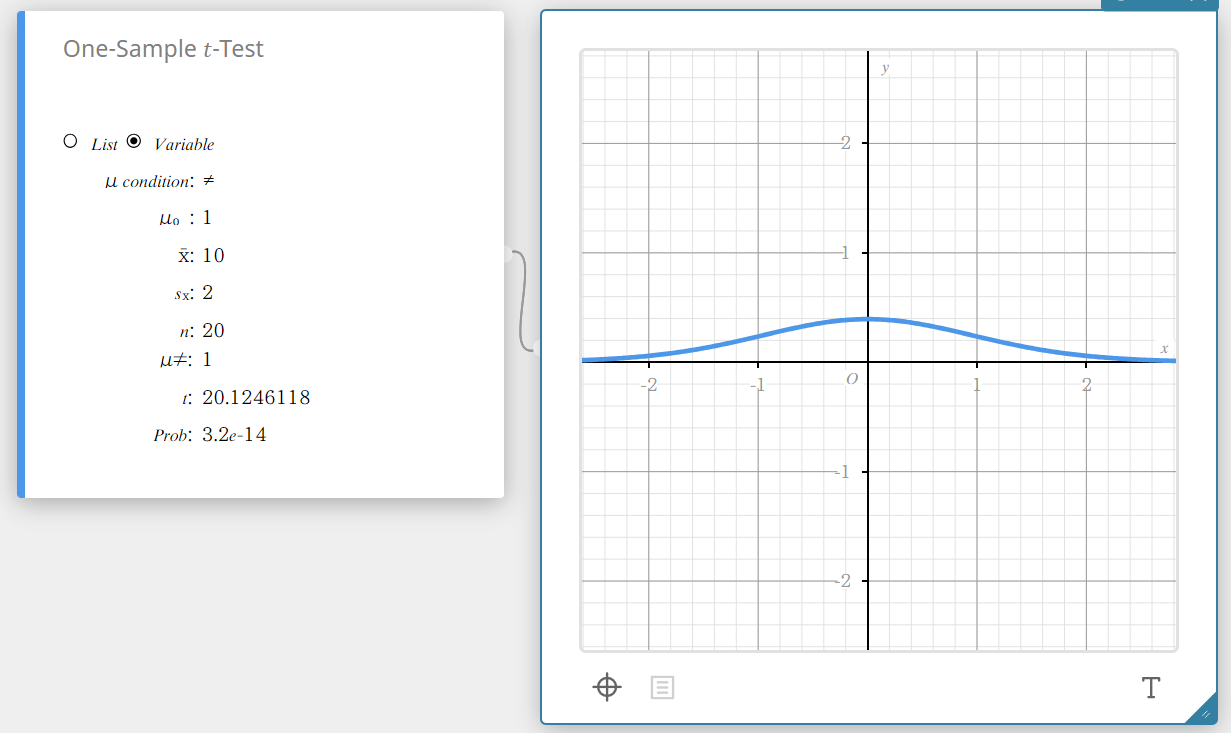
Gegevenstype: Variabele

• Invoertermen
  \(\mu\) condition : testvoorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  \(\mu_{0}\) : aangenomen gemiddelde populatie
  \(\overline{x}\) : steekproefgemiddelde
  \(s_{x}\) : standaardafwijking steekproef（\( s_{x} > 0 \)）
  \(n\) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  \(\mu \ne\) : testvoorwaarden van de gemiddelde waarde van de populatie
  \(t\) : \(t\)-waarde
  Prob : \(p\)-waarde

Gegevenstype: Lijst

• Invoertermen
  \(\mu\) condition : testvoorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  \(\mu_{0}\) : aangenomen gemiddelde populatie
  List : gegevenslijst
  Freq : frequentie (1 of lijstnaam)

• Uitvoertermen
  \(\mu \ne\) : testvoorwaarden van de gemiddelde waarde van de populatie
  \(t\) : \(t\)-waarde
  Prob : \(p\)-waarde
  \(\overline{x}\) : steekproefgemiddelde
  \(s_{x}\) : standaardafwijking steekproef
  \(n\) : grootte van de steekproef

\(t\)-test van twee steekproeven
Dit test het verschil tussen twee gemiddelden wanneer de standaardafwijkingen van de twee populaties onbekend zijn. De \(t\)-verdeling wordt gebruikt voor de \(t\)-test van twee steekproeven.

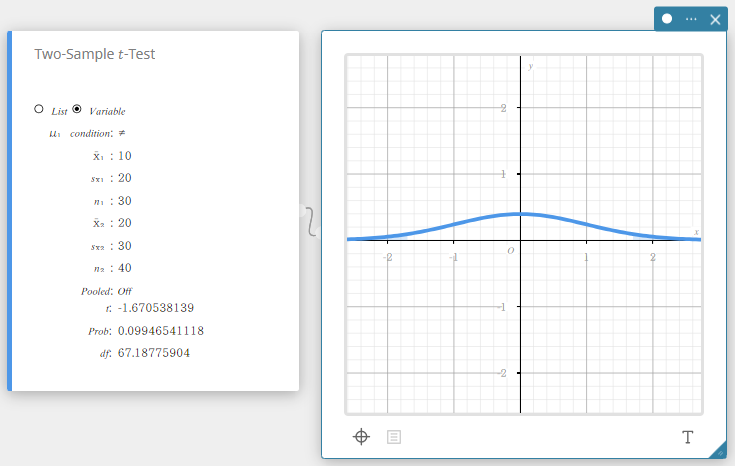
• Wanneer de twee standaardafwijkingen van de populaties identiek zijn (gecumuleerd)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{{s_{p}}^2 \left(\displaystyle \frac{1}{n_1} + \displaystyle \frac{1}{n_2} \right)}}\)
  \(df=n_1+n_2-2\)
  \(s_p=\sqrt{ \displaystyle \frac{(n_1-1){s_{x_1}}^2 + (n_2-1){s_{x_2}}^2}{n_1+n_2-2} }\)

• Wanneer de twee standaardafwijkingen van de populaties niet identiek zijn (niet gecumuleerd)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{\displaystyle \frac{{s_{x_1}}^2}{n_1} + \displaystyle \frac{{s_{x_2}}^2}{n_2}}}\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{(1-C)^2}{n_2-1}}\)
  \(C =\displaystyle \frac{\displaystyle \frac{{s_{x_1}}^2}{n_1}}{\displaystyle \frac{{s_{x_1}}^2}{n_1} +\displaystyle \frac{{s_{x_2}}^2}{n_2}}\)

\(x_1\): steekproefgemiddelde van gegevens van steekproef 1
\(x_2\): steekproefgemiddelde van gegevens van steekproef 2
\(s_{x_1}\) : standaardafwijking van steekproef 1
\(s_{x_2}\) : standaardafwijking van steekproef 2
\(s_p\) : gecumuleerde standaardafwijking van steekproef
\(n_1\) : grootte van steekproef 1
\(n_2\) : grootte van steekproef 2

Gegevenstype: Variabele

• Invoertermen
  \(\mu_1\) condition : voorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 kleiner is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2.)
  \(\overline{x}_1\) : steekproefgemiddelde van gegevens van steekproef 1
  \(s_{x_1}\) : standaardafwijking van steekproef 1（\(s_{x_1} > 0\)）
  \(n_1\) : grootte van steekproef 1 (positief geheel getal)
  \(\overline{x}_2\) : steekproefgemiddelde van gegevens van steekproef 2
  \(s_{x_2}\) : standaardafwijking van steekproef 2（\(s_{x_2} > 0\)）
  \(n_2\) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  \(t\) : \(t\)-waarde
  Prob : \(p\)-waarde
  \(df\) : vrijheidsgraden
  \(s_p\) : gecumuleerde standaardafwijking van steekproef

Gegevenstype: Lijst

• Invoertermen
  \(\mu_1\) condition : voorwaarden voor de gemiddelde waarde van de populatie (“\(\neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 kleiner is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2.)
  List(1) : lijst met gegevens van steekproef 1
  List(2) : lijst met gegevens van steekproef 2
  Freq(1) : steekproeffrequentie 1 (1 of lijstnaam)
  Freq(2) : steekproeffrequentie 2 (1 of lijstnaam)
  Pooled : On (gelijke varianties) of Off (ongelijke varianties)

• Uitvoertermen
  \(t\) : \(t\)-waarde
  Prob : \(p\)-waarde
  \(df\) : vrijheidsgraden
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( s_{x_{1}} \) : standaardafwijking van steekproef 1
  \( s_{x_{2}} \) : standaardafwijking van steekproef 2
  \(s_p\) : gecumuleerde standaardafwijking van steekproef
  \( n_{1} \) : grootte van steekproef 1
  \( n_{2} \) : grootte van steekproef 2

\(t\)-test van lineaire reg (\(t\)-test voor lineaire regressie)
Dit test de lineaire verhouding tussen de gekoppelde variabelen ( x , y ). De methode van de kleinste kwadraten wordt gebruikt om a en b te bepalen, die de coëfficiënten zijn van de regressieformule \(y = a + b \cdot x\). De p-waarde is de kans van de regressiehelling van de steekproef (b) op voorwaarde dat de nulhypothese waar is, \(\beta = 0\). De t-verdeling wordt gebruikt voor de \(t\)-test voor lineaire regressie.

\(t=r\sqrt{\displaystyle \frac{n-2}{1-r^2}}\)
\( \displaystyle b=\left\{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) \right\} / \left\{\sum_{i=1}^n (x_i-\overline{x})^2 \right\}\)
\(a=\overline{y}-b\overline{x}\)

\(a\) : regressieconstante (y-snijpunt)
\(b\) : regressiecoëfficiënt (helling)
\(n\) : grootte van steekproef（\(n \ge 3\)）
\(r\) : correlatiecoëfficiënt
\(r^2\) : determinatiecoëfficiënt

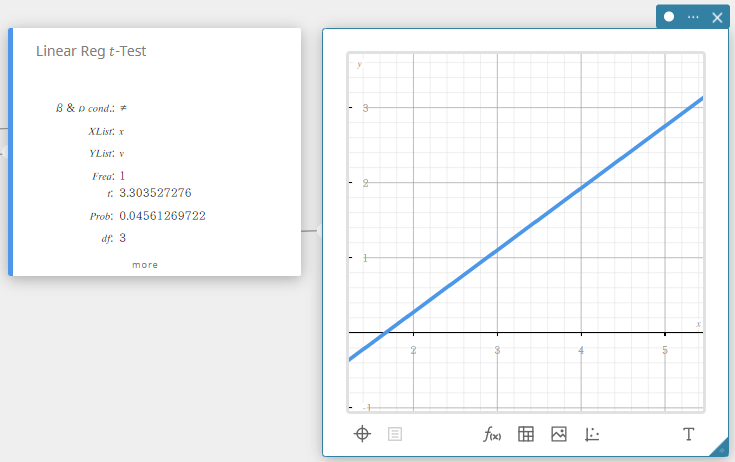
• Invoertermen
  \(\beta\ \&\ \rho\) cond : testvoorwaarden (“\(\neq\)” specifieert tweezijdige test, “<” specifieert onderste eenzijdige test, “>” specifieert bovenste eenzijdige test.)
  XList : x -gegevenslijst
  YList : y -gegevenslijst
  Freq : frequentie (1 of lijstnaam)

• Uitvoertermen
  \(t\) : \(t\)-waarde
  Prob : \(p\)-waarde
  \(df\) : vrijheidsgraden
  \(a\) : regressieconstante (y-snijpunt)
  \(b\) : regressiecoëfficiënt (helling)
  se : standaardfout van schatting over de regressielijn van de kleinste kwadraten
  \(r\) : correlatiecoëfficiënt
  \(r^2\) : determinatiecoëfficiënt
  SEb: standaardfout van de helling van de kleinste kwadraten

\(\chi^2\) Test
Dit test de onafhankelijkheid van twee categorische variabelen in een matrixvorm. De \(\chi^2\) test voor onafhankelijkheid vergelijkt de waargenomen matrix met de verwachte theoretische matrix. De \(\chi^2\) verdeling wordt gebruikt voor de \(\chi^2\) test.

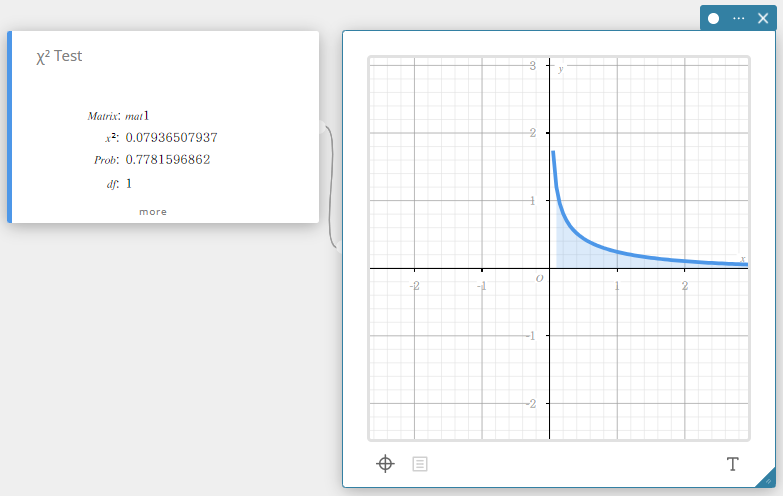
OPMERKING
De minimale grootte van de matrix is 1×2. Er doet zich een fout voor als de matrix slechts één kolom heeft.
Het resultaat van de verwachte frequentieberekening wordt opgeslagen in de systeemvariabele met als naam “Expected”.

\( \chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{l} \displaystyle \frac{(x_{ij}-F_{ij})^2}{F_{ij}} \)
\( F_{ij}=\frac{{\displaystyle\sum_{i=1}^k}x_{ij}\times{\displaystyle\sum_{j=1}^lx_{ij}}}{{\displaystyle\sum_{i=1}^k}{\displaystyle\sum_{j=1}^l}x_{ij}} \)
\( x_{ij}\) : Het element in rij i , kolom j van de waargenomen matrix.
\( F_{ij}\) : Het element in rij i , kolom j van de verwachte matrix.

• Invoertermen
  Matrix: naam van de matrix met waargenomen waarden (positieve gehele getallen in alle cellen voor 2×2 en grotere matrices; positieve reële getallen voor matrices met één rij)

• Uitvoertermen
  \(\chi^2\) : \(\chi^2\) waarde
  Prob : \(p\)-waarde
  \(df\) : vrijheidsgraden
  Observed : de invoermatrix van waargenomen waarden
  Expected : de berekende matrix van verwachte waarden

\(\chi^2\) GOF-test (\(\chi^2\) Goodness-Of-Fit-test)
Dit test of de waargenomen telling van steekproefgegevens overeenstemt met een bepaalde verdeling. Het kan bijvoorbeeld worden gebruikt om te bepalen of ze overeenstemt met de normale verdeling of binomiale verdeling.


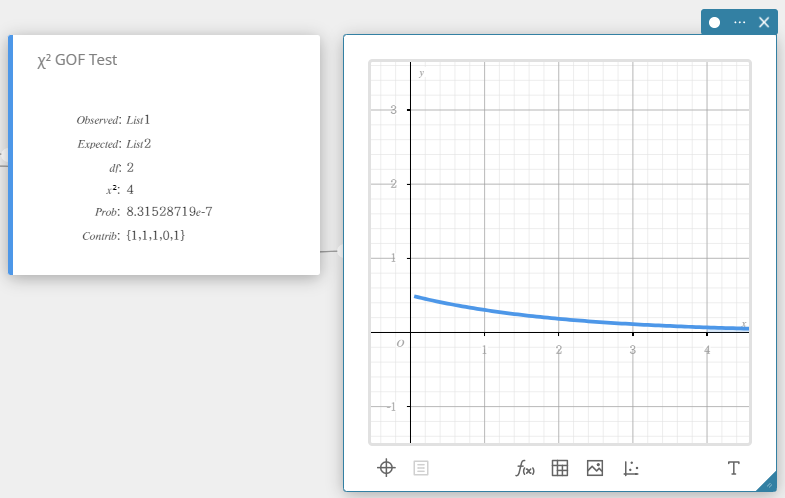
\(\chi^2=\sum_i^k \displaystyle \frac{ (O_i – E_i )^2 }{E_i}\)
\(Contrib = \left\{\displaystyle \frac{ (O_1 – E_1 )^2 }{E_1} \ \displaystyle \frac{ (O_2 – E_2 )^2 }{E_2} \cdots \displaystyle \frac{ (O_k – E_k )^2 }{E_k} \right\} \)

\(O_i\) : Het i-e element van de waargenomen lijst
\(E_i\) : Het i-e element van de verwachte lijst

• Invoertermen
  Observed list : naam van de lijst met waargenomen tellingen (alle cellen positieve gehele getallen)
  Expected list : naam van de lijst voor het opslaan van de verwachte frequentie
  \(df\) : vrijheidsgraden

• Uitvoertermen
  \(\chi^2\) : \(\chi^2\) waarde
  Prob : \(p\)-waarde
  \(df\) : vrijheidsgraden
  Contrib : naam van de lijst met de bijdrage van elke waargenomen telling

F-test van twee steekproeven
Dit test de verhouding tussen steekproefvarianties van twee onafhankelijke willekeurige steekproeven. De F-verdeling wordt gebruikt voor de F-test van twee steekproeven.

\( F=\displaystyle \frac{{S_{x_1}}^2}{{S_{x_2}}^2}\)

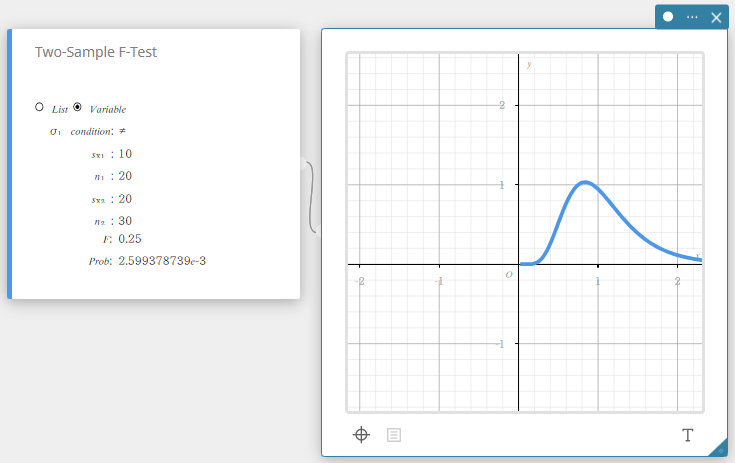
Gegevenstype: Variabele

• Invoertermen
  \( \sigma_1\) condition: testvoorwaarden voor standaardafwijking van populatie (“\( \neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 kleiner is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2.)
  \( s_{x_1}\) : standaardafwijking van steekproef 1（ \( s_{x_1} > 0\)）
  \( n_1\) : grootte van steekproef 1 (positief geheel getal)
  \( s_{x_2}\) : standaardafwijking van steekproef 2（ \( s_{x_2} > 0\)）
  \( n_2\) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  \( F\) : F-waarde
  Prob : p-waarde

Gegevenstype: Lijst

• Invoertermen
  \( \sigma_1\) condition: testvoorwaarden voor standaardafwijking van populatie (“\( \neq\)” specifieert tweezijdige test, “<” specifieert test waarbij steekproef 1 kleiner is dan steekproef 2, “>” specifieert test waarbij steekproef 1 groter is dan steekproef 2.)
  List(1) : lijst met gegevens van steekproef 1
  List(2) : lijst met gegevens van steekproef 2
  Freq(1) : steekproeffrequentie 1 (1 of lijstnaam)
  Freq(2) : steekproeffrequentie 2 (1 of lijstnaam)

• Uitvoertermen
  \( F\) : F-waarde
  Prob : p-waarde
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( s_{x_{1}} \) : standaardafwijking van steekproef 1
  \( s_{x_{2}} \) : standaardafwijking van steekproef 2
  \( n_{1} \) : grootte van steekproef 1
  \( n_{2} \) : grootte van steekproef 2

Eenwegs ANOVA (Eenwegsanalyse van variantie)
Dit test de hypothese dat de populatiegemiddelden van meerdere populaties identiek zijn. Het vergelijkt het gemiddelde van een of meer groepen op basis van één onafhankelijke variabele of factor.

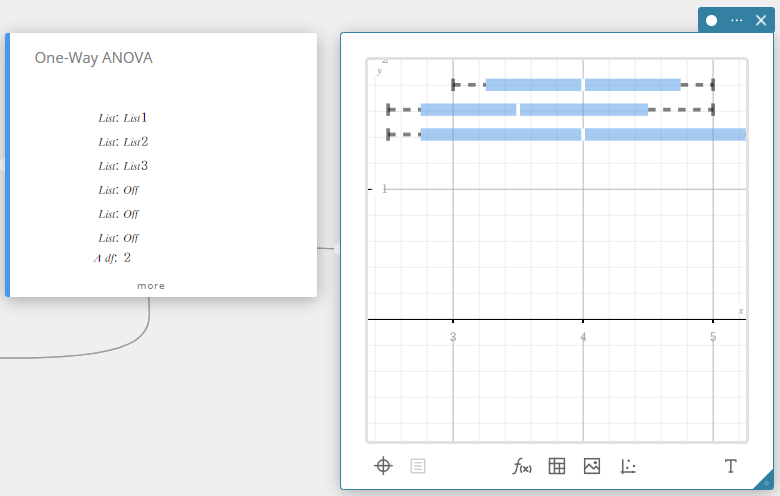
• Invoertermen
  FactorList(A) : lijst met de niveaus van Factor A
  DependentList: lijst met de gegevens van de steekproef

• Uitvoertermen
  A df : vrijheidsgraden van Factor A
  A MS : gemiddeld kwadraat van Factor A
  A SS : som van de kwadraten van Factor A
  A F : F-waarde van Factor A
  A p : p-waarde van Factor A
  Err df : vrijheidsgraden van fout
  Err MS : gemiddeld kwadraat van fout
  Err SS : som van de kwadraten van fout

Tweewegs ANOVA (Tweewegsanalyse van variantie)
Dit test de hypothese dat de populatiegemiddelden van meerdere populaties identiek zijn. Het onderzoekt het effect van elke variabele afzonderlijk evenals hun interactie met elkaar op basis van een afhankelijke variabele.

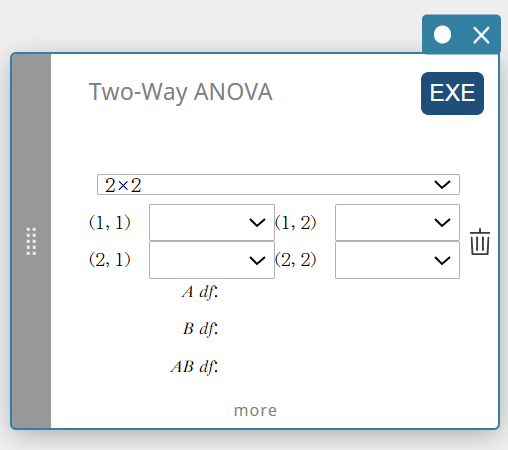
• Invoertermen
  2×2: type gegevenstabel
  FactorList(A) : lijst met de niveaus van Factor A
  FactorList(B) : lijst met de niveaus van Factor B
  DependentList: lijst met de gegevens van de steekproef

• Uitvoertermen
  A df : vrijheidsgraden van Factor A
  A MS : gemiddeld kwadraat van Factor A
  A SS : som van de kwadraten van Factor A
  A F : F-waarde van Factor A
  A p : p-waarde van Factor A
  B df : vrijheidsgraden van Factor B
  B MS : gemiddeld kwadraat van Factor B
  B SS : som van de kwadraten van Factor B
  B F : F-waarde van Factor B
  B p : p-waarde van Factor B
  AB df : vrijheidsgraden van Factor A × Factor B
  AB MS : gemiddeld kwadraat van Factor A × Factor B
  AB SS : som van de kwadraten van Factor A × Factor B
  AB F : F-waarde van Factor A × Factor B
  AB p : p-waarde van Factor A × Factor B
  Err df : vrijheidsgraden van fout
  Err MS : gemiddeld kwadraat van fout
  Err SS : som van de kwadraten van fout

Vertrouwensintervallen

Z-interval van één steekproef
Dit berekent het betrouwbaarheidsinterval voor de gemiddelde populatie op basis van een steekproefgemiddelde en bekende standaardafwijking van de populatie.

\(Lower = \overline{x}-Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(Upper = \overline{x}+Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(\alpha\) is het significantieniveau en \(100(1 – \alpha)\%\) is het vertrouwelijkheidsniveau. Wanneer het vertrouwelijksheidsniveau bijvoorbeeld \(95\%\) is, voert u 0,95 in, wat α = 1 – 0,95 = 0,05 oplevert.

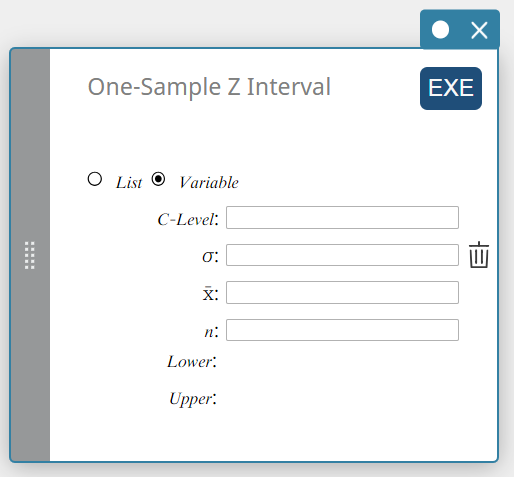
Gegevenstype: Variabele

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : standaardafwijking van de populatie（\( \sigma > 0 \)）
  \( \overline{x} \) : steekproefgemiddelde
  \( n \) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)

Gegevenstype: Lijst

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : standaardafwijking van de populatie（\( \sigma > 0 \)）
  List: lijst met gegevens van steekproef
  Freq : steekproeffrequentie (1 of lijstnaam)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \( \overline{x} \) : steekproefgemiddelde
  \( s_{x} \) : standaardafwijking steekproef
  \( n \) : grootte van de steekproef

Z-interval van twee steekproeven
Dit berekent het betrouwbaarheidsinterval voor het verschil tussen populatiegemiddelden op basis van het verschil tussen steekproefgemiddelden wanneer de standaardafwijkingen van de populatie bekend zijn.


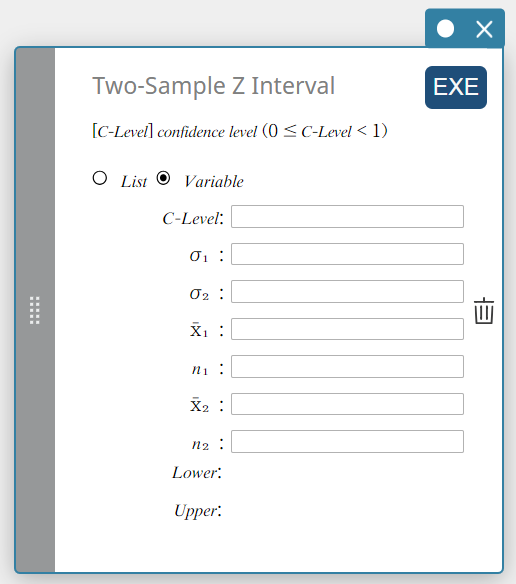
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)

Gegevenstype: Variabele

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : standaardafwijking van steekproef 1 van populatie（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : standaardafwijking van steekproef 2 van populatie（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( n_{1} \) : grootte van steekproef 1 (positief geheel getal)
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( n_{2} \) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)

Gegevenstype: Lijst

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : standaardafwijking van steekproef 1 van populatie（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : standaardafwijking van steekproef 2 van populatie（\( \sigma_{2} > 0 \)）
  List(1) : lijst met gegevens van steekproef 1
  List(2) : lijst met gegevens van steekproef 2
  Freq(1) : steekproeffrequentie 1 (1 of lijstnaam)
  Freq(2) : steekproeffrequentie 2 (1 of lijstnaam)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( s_{x_{1}} \) : standaardafwijking van steekproef 1
  \( s_{x_{2}} \) : standaardafwijking van steekproef 2
  \( n_{1} \) : grootte van steekproef 1
  \( n_{2} \) : grootte van steekproef 2

Z-interval van één voorwerp (Z-interval van één voorwerp)
Dit berekent het betrouwbaarheidsinterval voor het populatiegedeelte op basis van één steekproefgedeelte.


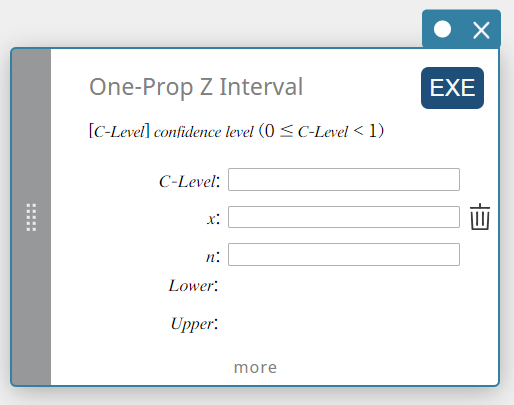
\(Lower =\displaystyle \frac{x}{n}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
\(Upper =\displaystyle \frac{x}{n}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( x \) : gegevens (0 of positief geheel getal)
  \( n \) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \(\hat{p}\) : verwacht gedeelte van steekproef

Z-interval van twee voorwerpen (Z-interval van twee voorwerpen)
Dit berekent het betrouwbaarheidsinterval voor het verschil tussen populatiegedeelten op basis van het verschil tussen het Z-interval van twee voorwerpen.


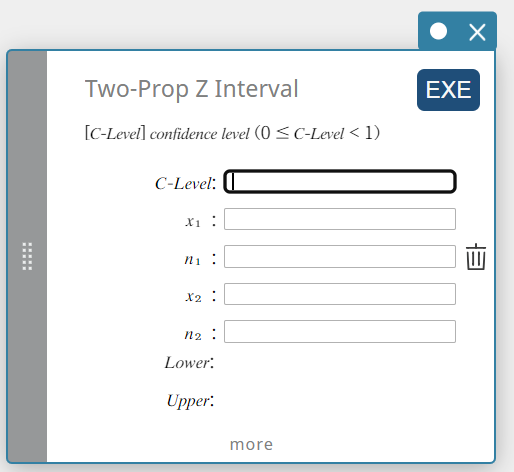
\( Lower =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1- \displaystyle\frac{x_1}{n_1} \right) }{n_1} + \displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1- \displaystyle \frac{x_2}{n_2} \right) }{n_2} } \)
\( Upper =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1-\displaystyle \frac{x_1}{n_1} \right) }{n_1} +\displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1-\displaystyle\frac{x_2}{n_2} \right) }{n_2} } \)

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \(x_{1}\) : gegevenswaarde van steekproef 1 (geheel getal, \(x_{1}\) moet kleiner of gelijk zijn aan \(n_{1}\))
  \(n_{1}\) : grootte van steekproef 1 (positief geheel getal)
  \(x_{2}\) : gegevenswaarde van steekproef 2 (geheel getal, \(x_{2}\) moet kleiner of gelijk zijn aan \(n_{2}\))
  \(n_{2}\) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \(\hat{p}_{1}\) : verwacht gedeelte van steekproef 1
  \(\hat{p}_{2}\) : verwacht gedeelte van steekproef 2

\(t\)-interval van één steekproef
Dit berekent het betrouwbaarheidsinterval voor de gemiddelde populatie op basis van een steekproefgemiddelde en een standaardafwijking van de steekproef wanneer de standaardafwijking van de populatie niet bekend is.

\(Lower = \overline{x}-t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
\(Upper = \overline{x}+t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)

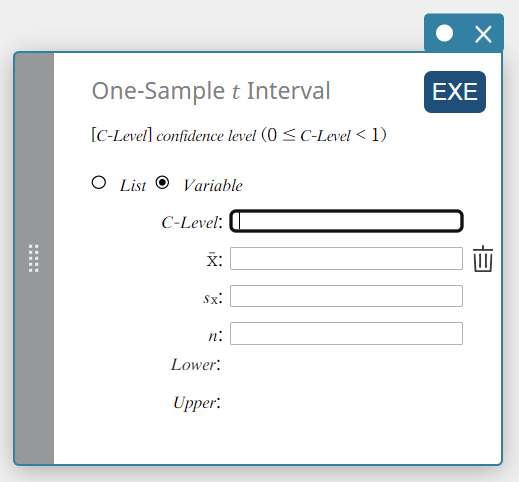
Gegevenstype: Variabele

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x} \) : steekproefgemiddelde
  \(s_{x}\) : standaardafwijking steekproef（\( s_{x} \ge 0 \)）
  \(n\) : grootte van de steekproef (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)

Gegevenstype: Lijst

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  List: lijst met gegevens van steekproef
  Freq : steekproeffrequentie (1 of lijstnaam)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \( \overline{x} \) : steekproefgemiddelde
  \( s_{x} \) : standaardafwijking steekproef
  \( n \) : grootte van de steekproef

\(t\)-interval van twee steekproeven
Dit berekent het betrouwbaarheidsinterval voor het verschil tussen populatiegemiddelden op basis van het verschil tussen steekproefgemiddelden en standaardafwijkingen van een steekproef wanneer de standaardafwijkingen van de populatie niet bekend zijn.

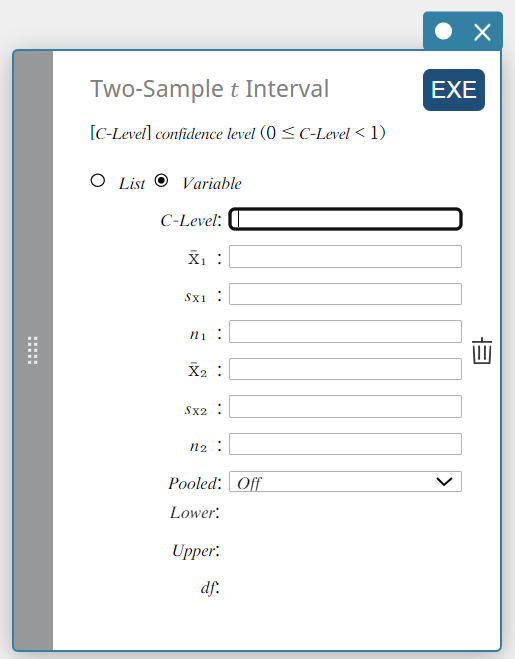
• Wanneer de twee standaardafwijkingen van de populaties identiek zijn (gecumuleerd)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  

• Wanneer de twee standaardafwijkingen van de populaties niet identiek zijn (niet gecumuleerd)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{ \left( 1-C \right) ^2}{n_2-1}}\)
  \(C=\displaystyle \frac{\displaystyle \frac{{S_{x_1}}^2}{n_1}}{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1} + \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  

Gegevenstype: Variabele

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \(s_{x_1}\) : standaardafwijking van steekproef 1（\(s_{x_1} \ge 0\)）
  \( n_{1} \) : grootte van steekproef 1 (positief geheel getal)
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \(s_{x_2}\) : standaardafwijking van steekproef 2（\(s_{x_2} \ge 0\)）
  \( n_{2} \) : grootte van steekproef 2 (positief geheel getal)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \(df\) : vrijheidsgraden
  \(s_p\) : gecumuleerde standaardafwijking van steekproef

Gegevenstype: Lijst

• Invoertermen
  C-Level : vertrouwelijkheidsniveau（\(0 \le\) C-Level \(\lt 1\)）
  List(1) : lijst met gegevens van steekproef 1
  List(2) : lijst met gegevens van steekproef 2
  Freq(1) : steekproeffrequentie 1 (1 of lijstnaam)
  Freq(2) : steekproeffrequentie 2 (1 of lijstnaam)
  Pooled : On (gelijke varianties) of Off (ongelijke varianties)

• Uitvoertermen
  Lower : interval benedengrens (linkerrand)
  Upper : interval bovengrens (rechterrand)
  \(df\) : vrijheidsgraden
  \( \overline{x}_{1} \) : steekproefgemiddelde van gegevens van steekproef 1
  \( \overline{x}_{2} \) : steekproefgemiddelde van gegevens van steekproef 2
  \( s_{x_{1}} \) : standaardafwijking van steekproef 1
  \( s_{x_{2}} \) : standaardafwijking van steekproef 2
  \(s_p\) : gecumuleerde standaardafwijking van steekproef
  \( n_{1} \) : grootte van steekproef 1
  \( n_{2} \) : grootte van steekproef 2

Verdeling

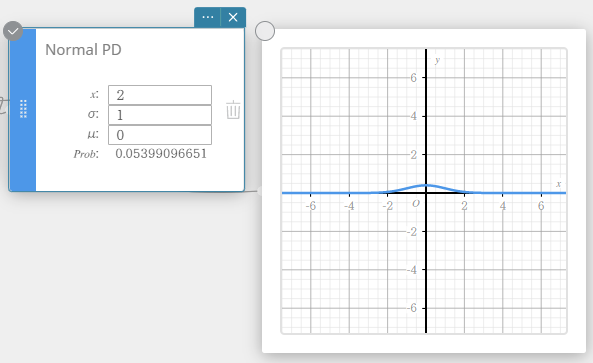
Normale PD (Normale kansdichtheid)
Dit berekent de normale kansdichtheid voor een opgegeven waarde.
Als u σ = 1 en μ= 0 opgeeft, verkrijgt u de standaard normale verdeling.

\(\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \qquad (\sigma>0)\)

• Invoertermen
  \( x \) : gegevenswaarde
  \( \sigma \) : standaardafwijking populatie (\( \sigma > 0 \)）
  \( \mu \) : gemiddelde populatie

• Uitvoertermen
  Prob : normale kansdichtheid

Normale CD (Normale cumulatieve verdeling)
Hiermee wordt de cumulatieve kans van een normale verdeling tussen een onderste grens ( a ) en een bovenste grens ( b ) berekend.

\(\displaystyle p=\frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{ \scriptscriptstyle -\frac{(x-\mu)^2}{2\sigma^2} }dx\)

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \( \sigma \) : standaardafwijking populatie (\( \sigma > 0 \)）
  \(\mu\) : gemiddelde populatie

• Uitvoertermen
  Prob : normale kansverdeling p
  z Low : gestandaardiseerde ondergrens van z-waarde
  z Up : gestandaardiseerde bovengrens van z-waarde

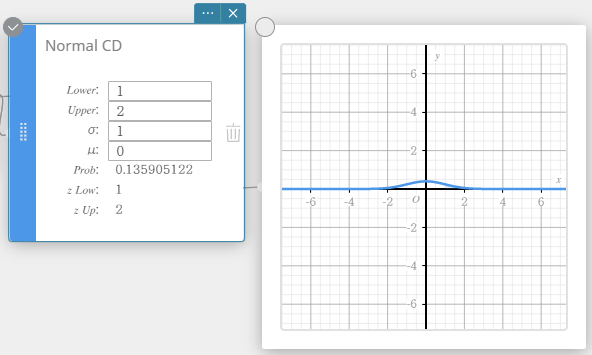
\(t\) PD van een student (\(t\) -kansdichtheid van een student)
Dit berekent de t-kansdichtheid van de student voor een specifieke waarde.


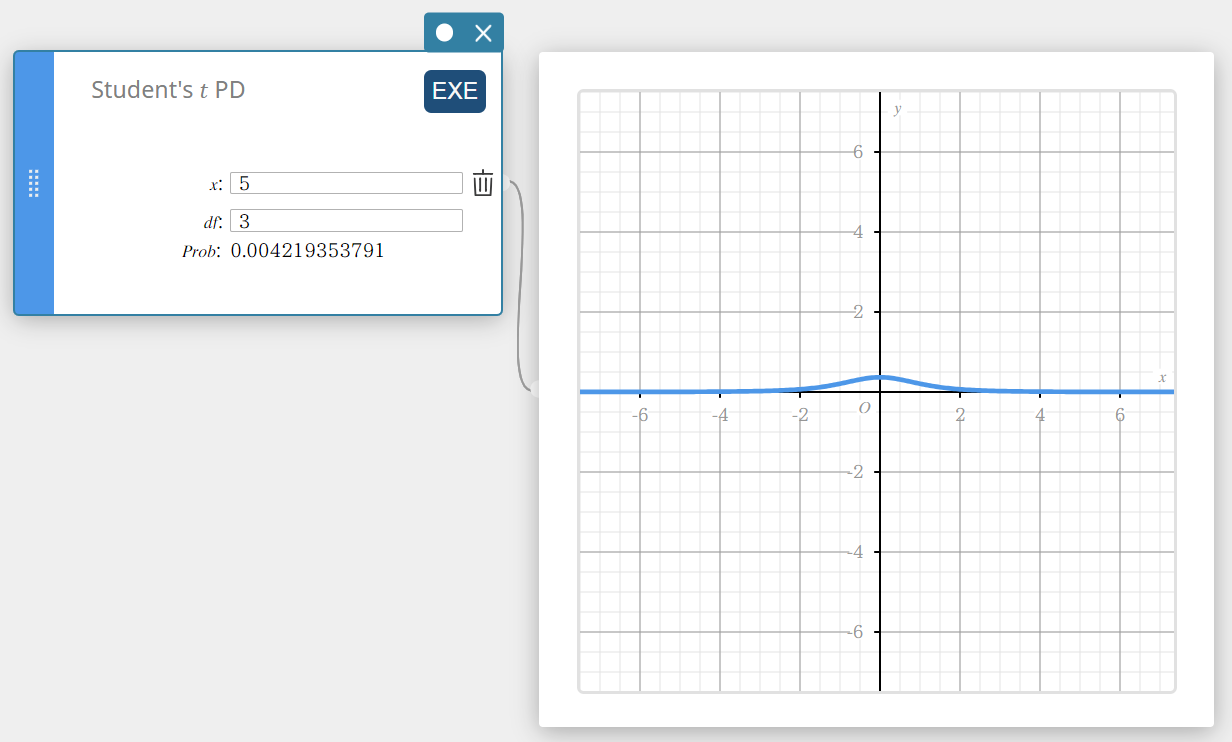
\(f(x)=\frac{\Gamma\left({\displaystyle\frac{df+1}2}\right)}{\Gamma\left({\displaystyle\frac{df}2}\right)}\times\frac{\left(1+{\displaystyle\frac{x^2}{df}}\right)^{-{\displaystyle\frac{df+1}2}}}{\sqrt{\pi\cdot df}}\)

• Invoertermen
  \( x \) : gegevenswaarde
  \(df\) : vrijheidsgraden（\(df \gt 0\)）

• Uitvoertermen
  Prob : t-kansdichtheid van een student

\(t\) CD van een student (\(t\)-cumulatieve verdeling van een student)
Hiermee wordt de cumulatieve kans van de t-verdeling van een student tussen een onderste grens ( a ) en een bovenste grens ( b ) berekend.


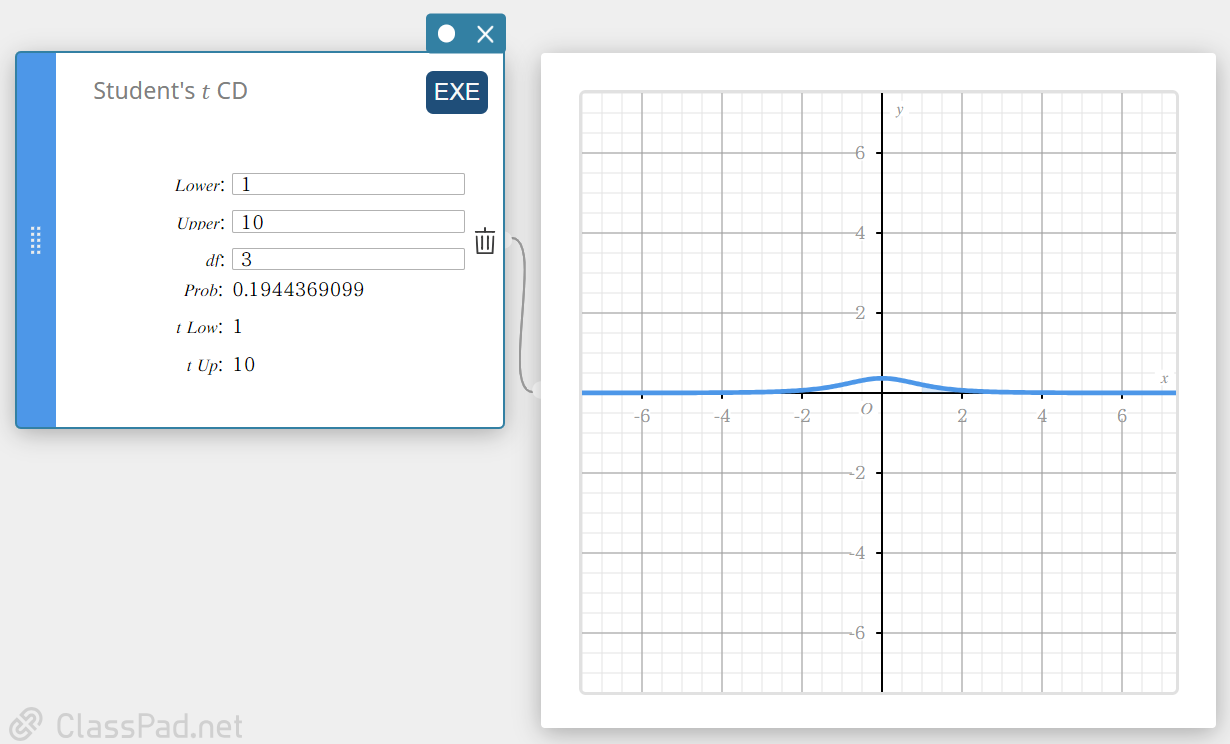
\( p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{df+1}{2} \right) }{\Gamma \left(\displaystyle \frac{df}{2} \right) \sqrt{\pi \cdot df}}\int_a^b \left(\displaystyle 1+\frac{x^2}{df} \right) ^{-\displaystyle\frac{df+1}{2}}dx \)

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \(df\) : vrijheidsgraden（\(df \gt 0\)）

• Uitvoertermen
  Prob : t-verdeling van een student
  t Low : door u ingevoerde waarde van de onderste grens
  t Up : door u ingevoerde waarde van de bovenste grens

\(\chi^2\) PD (\(\chi^2\) kansdichtheid)
Dit berekent de \(\chi^2\) kansdichtheid voor een opgegeven waarde.


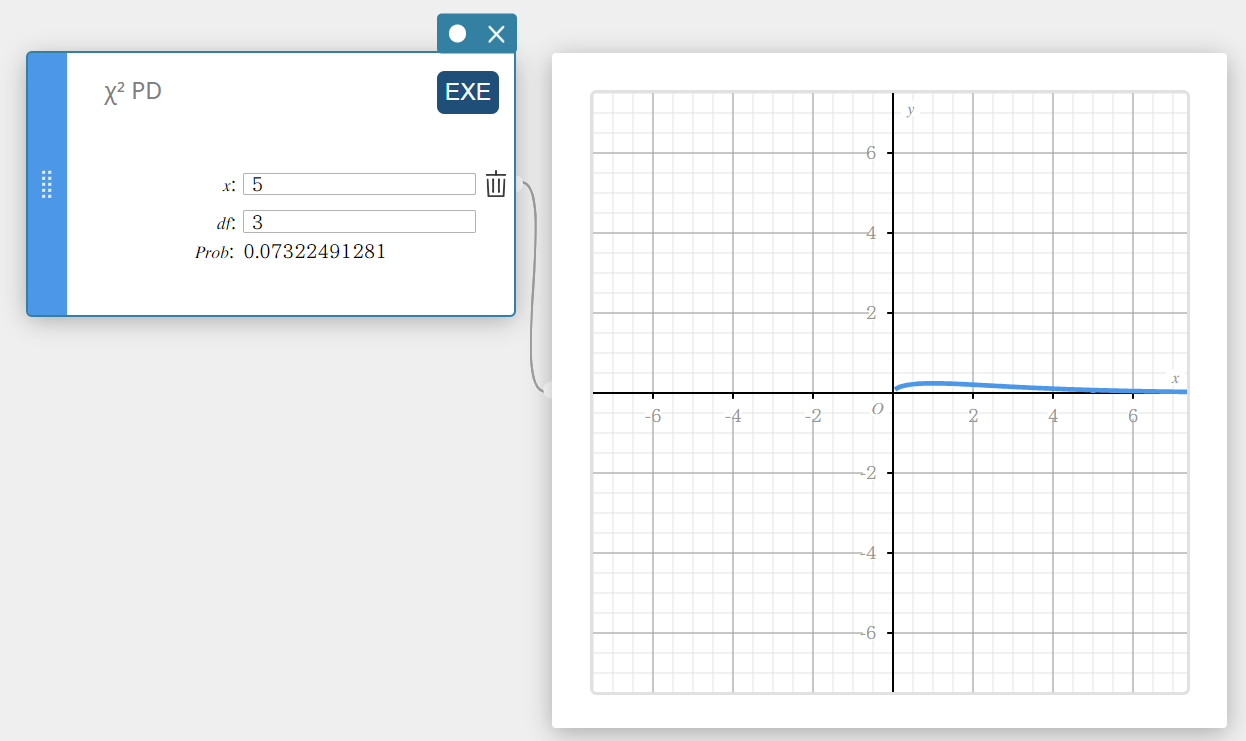
\(f \left( x \right) =\displaystyle\frac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}\)

• Invoertermen
  \( x \) : gegevenswaarde
  \(df\) : vrijheidsgraden (positief geheel getal)

• Uitvoertermen
  Prob : \(\chi^2\) kansdichtheid

\(\chi^2\) CD (\(\chi^2\) cumulatieve verdeling)
Dit berekent de cumulatieve kans van een \(\chi^2\) verdeling tussen een onderste grens en een bovenste grens.


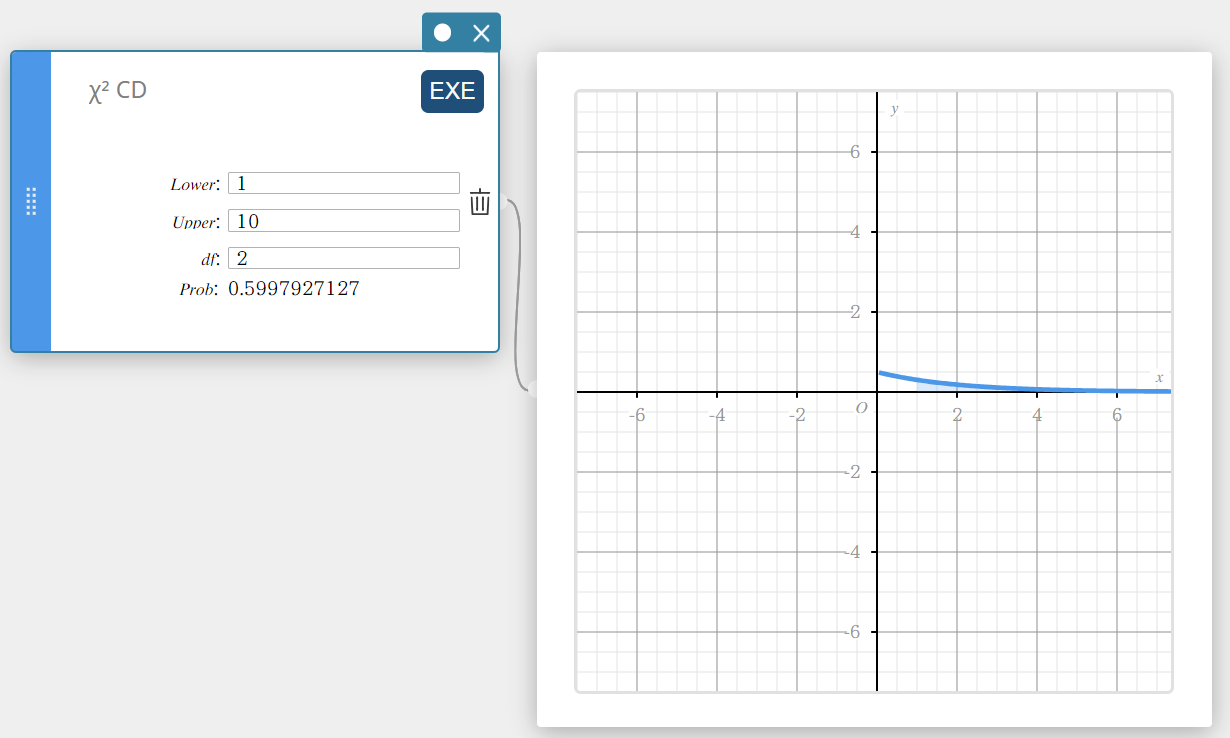
\(p=\cfrac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}\int_a^b x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}dx\)

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \(df\) : vrijheidsgraden (positief geheel getal)

• Uitvoertermen
  Prob : \(\chi^2\) kansdichtheid

F PD (F-kansdichtheid)
Dit berekent de F-kansdichtheid voor een opgegeven waarde.


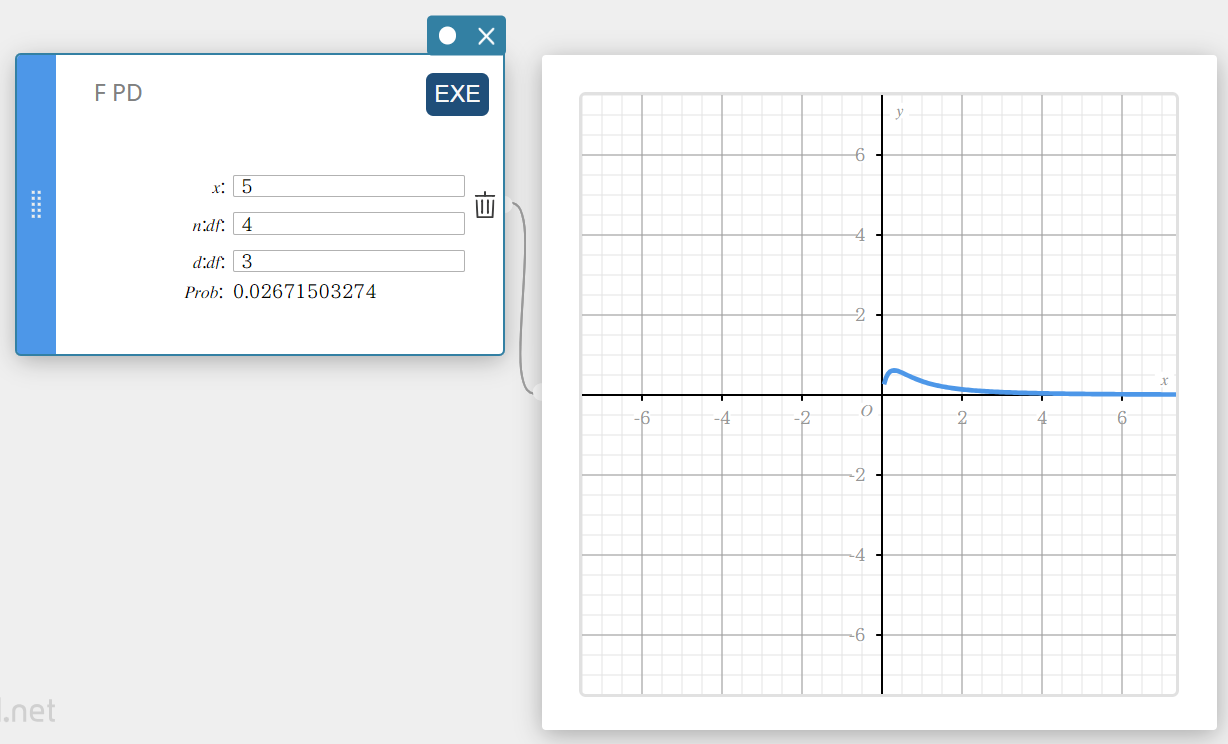
\(f(x)=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}\)

• Invoertermen
  \( x \) : gegevenswaarde
  \( n:df \) : vrijheidsgraden van teller (positief geheel getal)
  \( d:df \) : vrijheidsgraden van noemer (positief geheel getal)

• Uitvoertermen
  Prob : F-kansdichtheid

F CD (F cumulatieve verdeling)
Dit berekent de cumulatieve kans van een F-verdeling tussen een onderste grens en een bovenste grens.


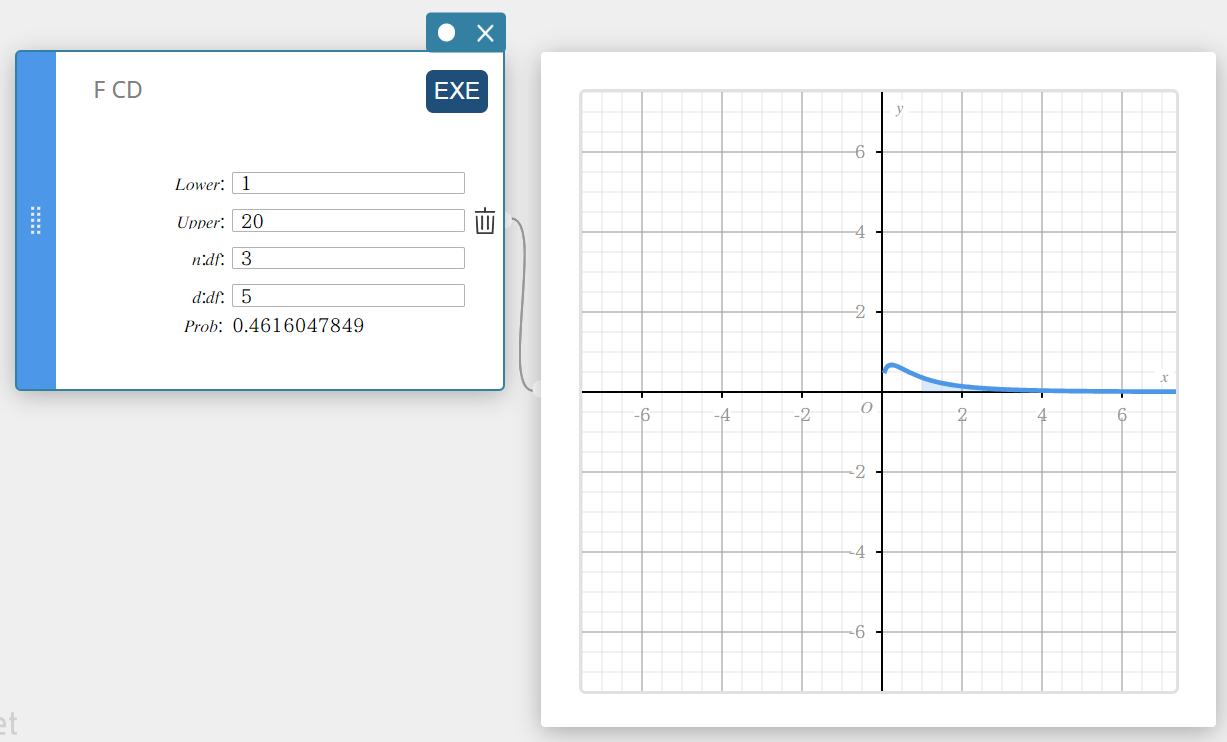
\(p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}\int_a^b x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}dx\)

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \( n:df \) : vrijheidsgraden van teller (positief geheel getal)
  \( d:df \) : vrijheidsgraden van noemer (positief geheel getal)

• Uitvoertermen
  Prob : F-kansverdeling

Binomiale PD (Binomiale kansverdeling)
Dit berekent de kans in een binomiale kansverdeling dat het succes zal voorkomen bij een specifieke proef.


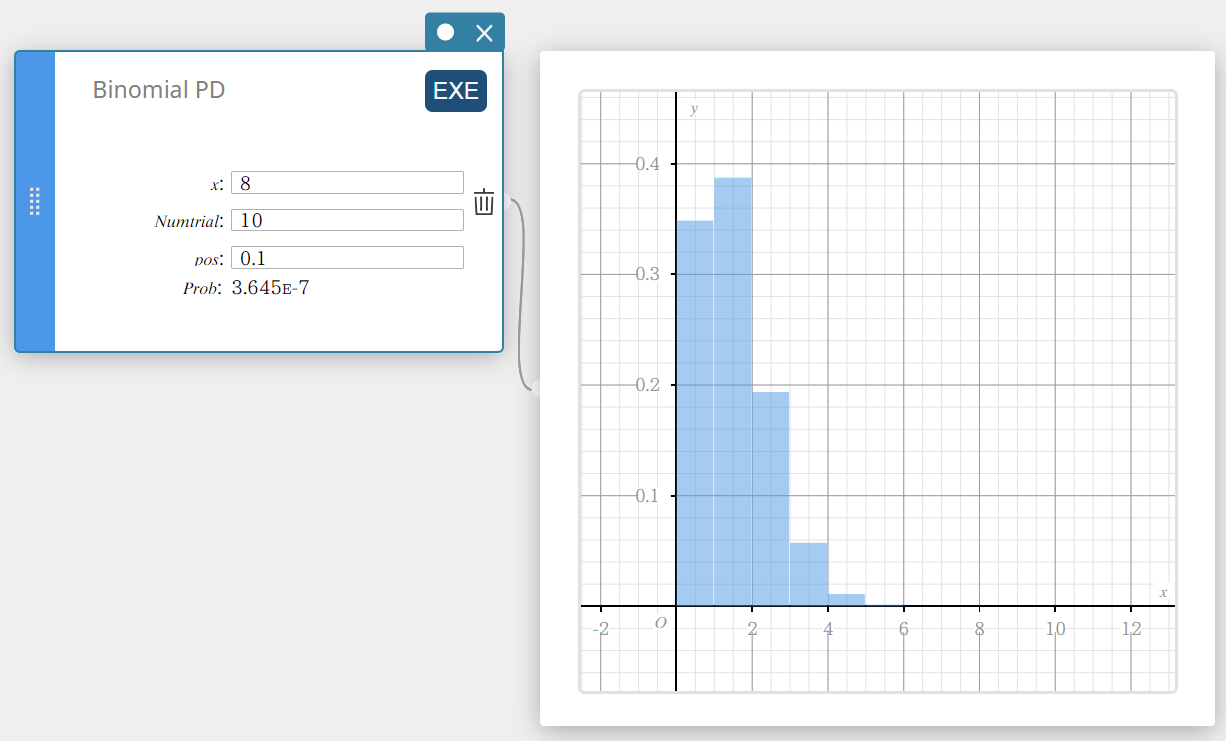
\(f(x)={}_nC_xp^x(1-p)^{n-x} \quad (x=0,1, \cdots,n)\)

\(p\) : kans op succes（(0 \(≤\) p \(≤\) 1)
\(n\) : aantal proeven

• Invoertermen
  \( x \) : vastgestelde proef (geheel getal van 0 tot n)
  Numtrial : aantal proeven n (geheel getal, n ≥ 0)
  pos : kans op succes p (0 \(≤\) p \(≤\) 1)

• Uitvoertermen
  Prob : binomiale waarschijnlijkheid

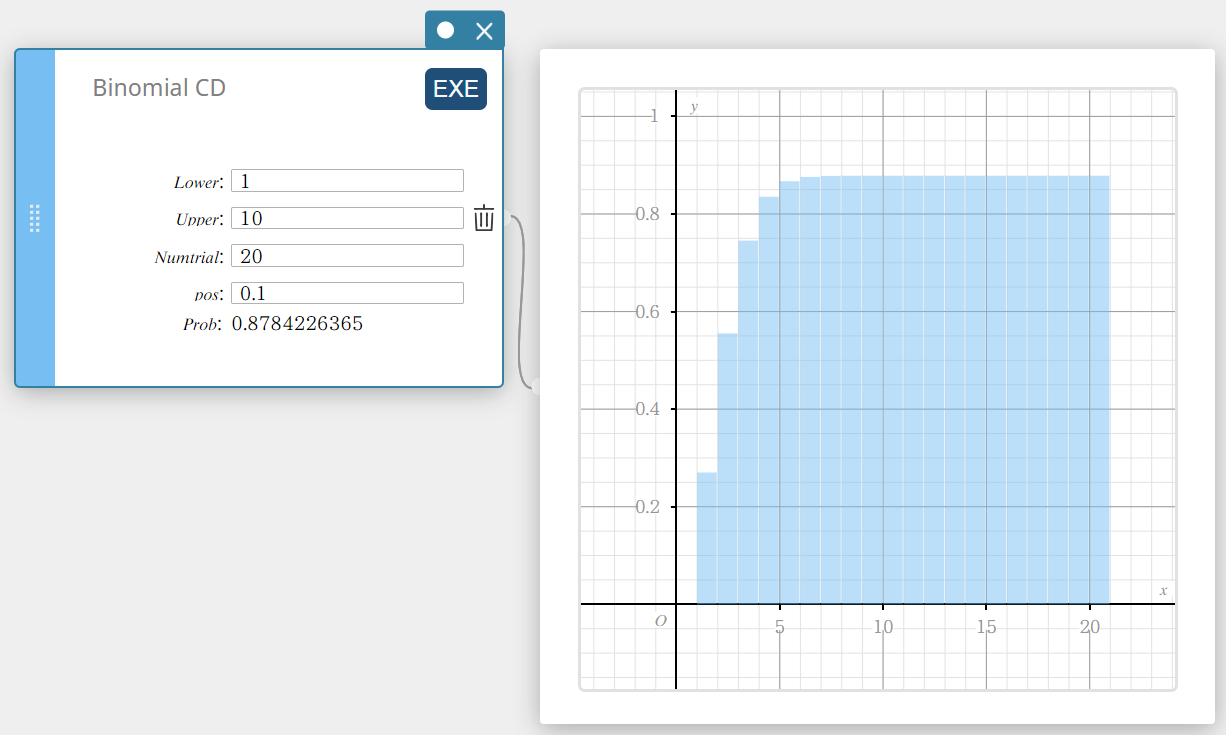
Binomiale CD (Binomiale cumulatieve verdeling)
Dit berekent de cumulatieve kans in een binomiale verdeling dat er succes zal zijn bij of vóór een specifieke proef.

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  Numtrial : aantal proeven n (geheel getal, n \(≥\) 1)
  pos : kans op succes p (0 \(≤\) p \(≤\) 1)

• Uitvoertermen
  Prob : binomiale cumulatieve waarschijnlijkheid

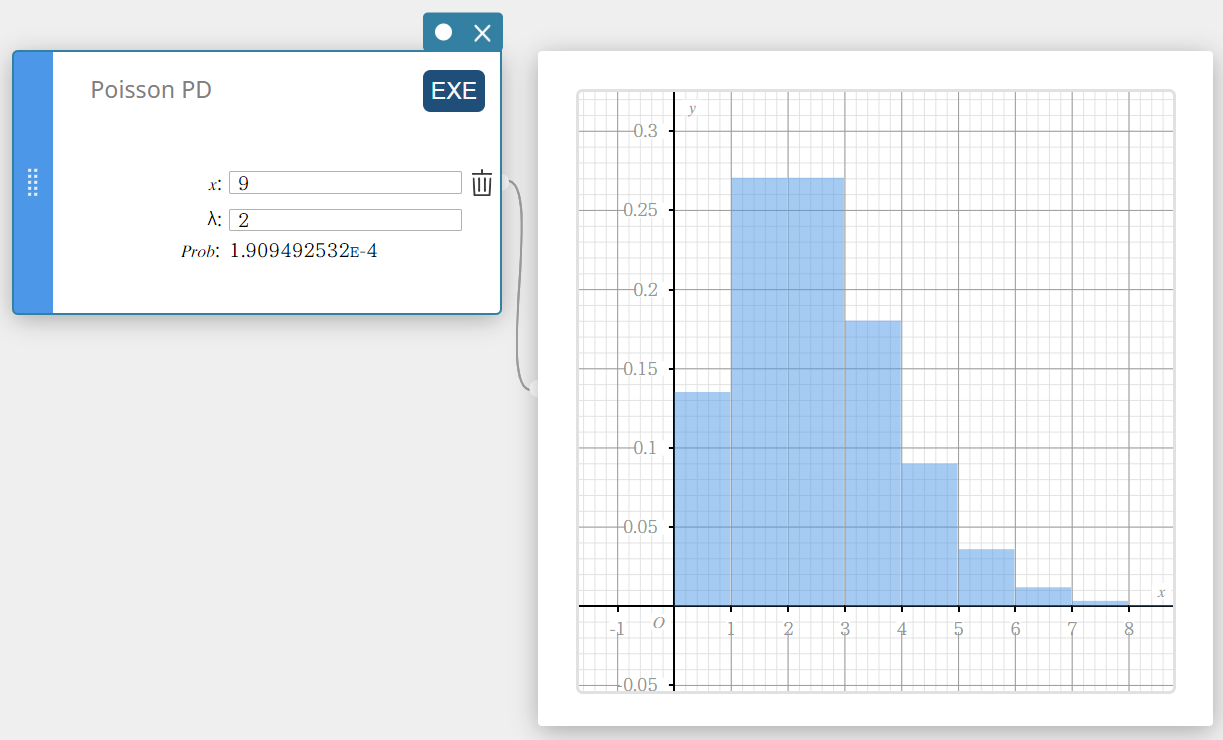
Poisson PD (Poisson-kansverdeling)
Dit berekent de kans in een Poisson-kansverdeling dat het succes zal voorkomen bij een specifieke proef.

\(f(x)=\displaystyle\frac{e^{-\lambda} \lambda^x}{x!} \qquad (x=0,1,2,\cdots)\)

• Invoertermen
  \( x \) : specifieke proef (geheel getal, x \(≥\) 0)
  \( \lambda \) : gemiddelde（\(\lambda \gt 0\)）

• Uitvoertermen
  Prob : Poisson-waarschijnlijkheid

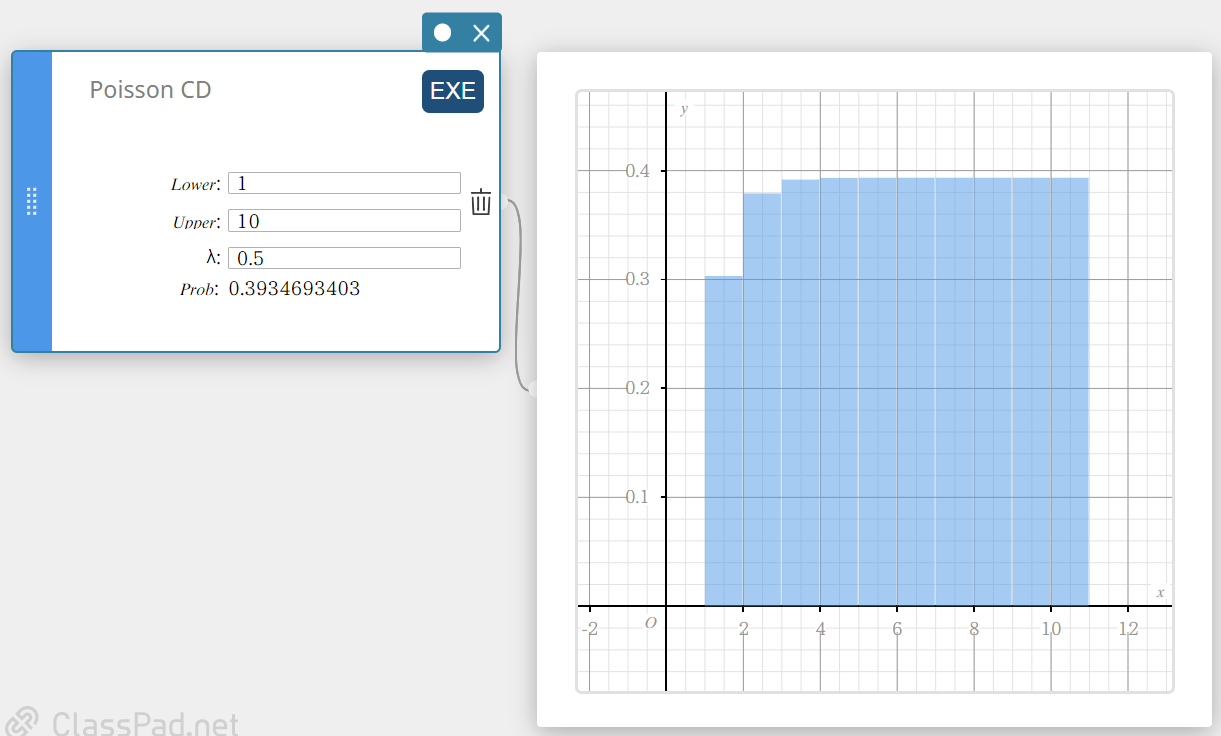
Poisson CD (Poisson cumulatieve verdeling)
Dit berekent de cumulatieve kans in een Poisson-verdeling dat er succes zal zijn bij of vóór een specifieke proef.

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \( \lambda \) : gemiddelde（\(\lambda \gt 0\)）

• Uitvoertermen
  Prob : Poisson cumulatieve waarschijnlijkheid

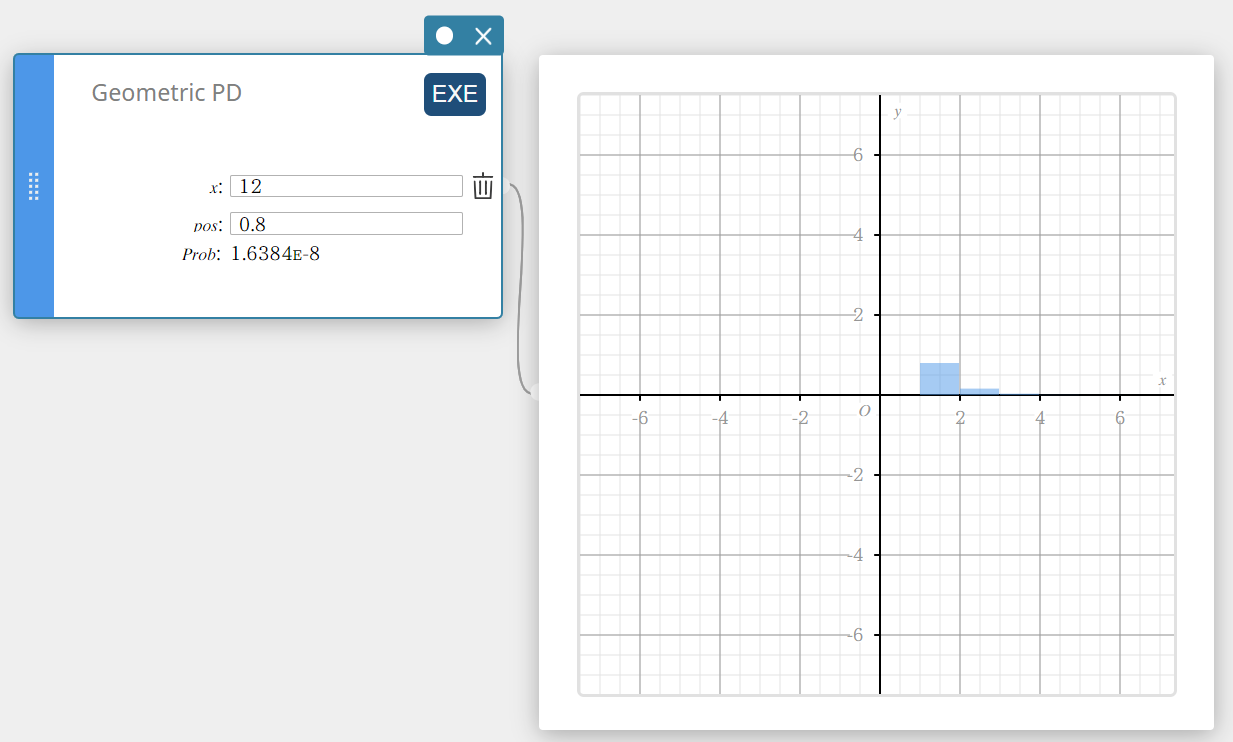
Geometrische PD (Geometrische kansverdeling)
Dit berekent de kans in een geometrische verdeling dat het succes zal voorkomen bij een specifieke proef.

\( f(x)=p(1-p)^{x-1} \qquad (x=1,2,3,\cdots) \)

• Invoertermen
  \( x \) : specifieke proef (positief geheel getal)
  pos : kans op succes p (0 \(≤\) p \(≤\) 1)

• Uitvoertermen
  Prob : geometrische waarschijnlijkheid

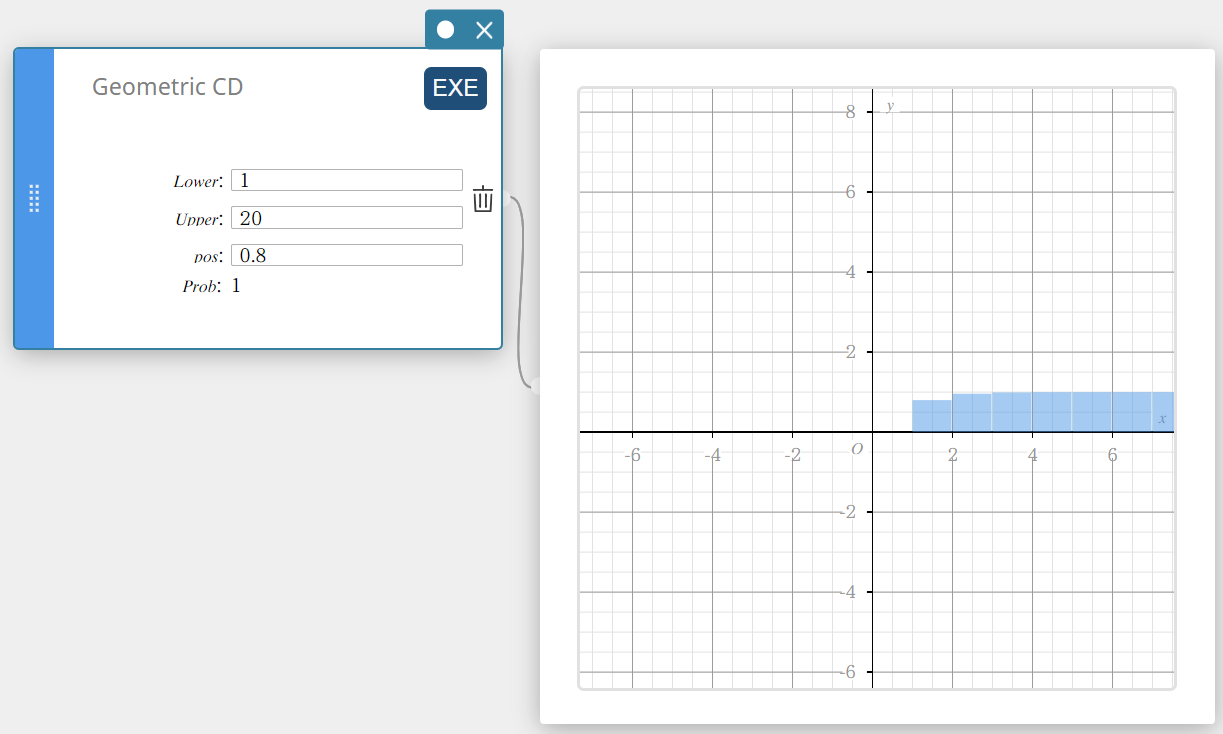
Geometrische CD (Geometrische cumulatieve verdeling)
Dit berekent de cumulatieve kans in een geometrische verdeling dat er succes zal zijn bij of vóór een specifieke proef.

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  pos : kans op succes p (0 \(≤\) p \(≤\) 1)

• Uitvoertermen
  Prob : geometrische cumulatieve waarschijnlijkheid

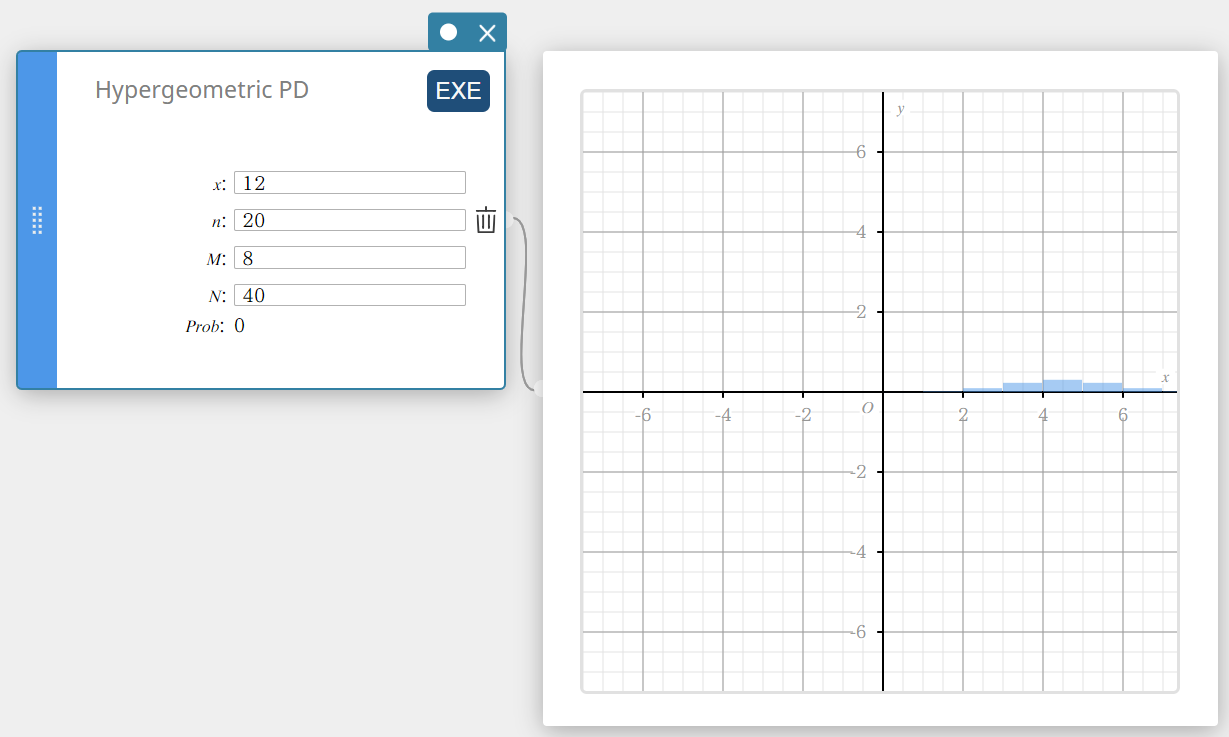
Hypergeometrische PD (hypergeometrische kansverdeling)
Dit berekent de kans in een hypergeometrische verdeling dat het succes zal voorkomen bij een specifieke proef.

\( prob = \displaystyle\frac{ {}_MC_x \times {}_{N-M}C_{n-x} }{ {}_NC_n } \)

• Invoertermen
  \(x\) : specifieke proef (geheel getal)
  \(n\) : aantal proeven van populatie (0 \(≤\) n geheel getal)
  \(M\) : aantal successen in populatie (0 \(≤\) M geheel getal)
  \(N\) : grootte van populatie ( n \(≤\) N , M \(≤\) N geheel getal)

• Uitvoertermen
  Prob : hypergeometrische kansverdeling

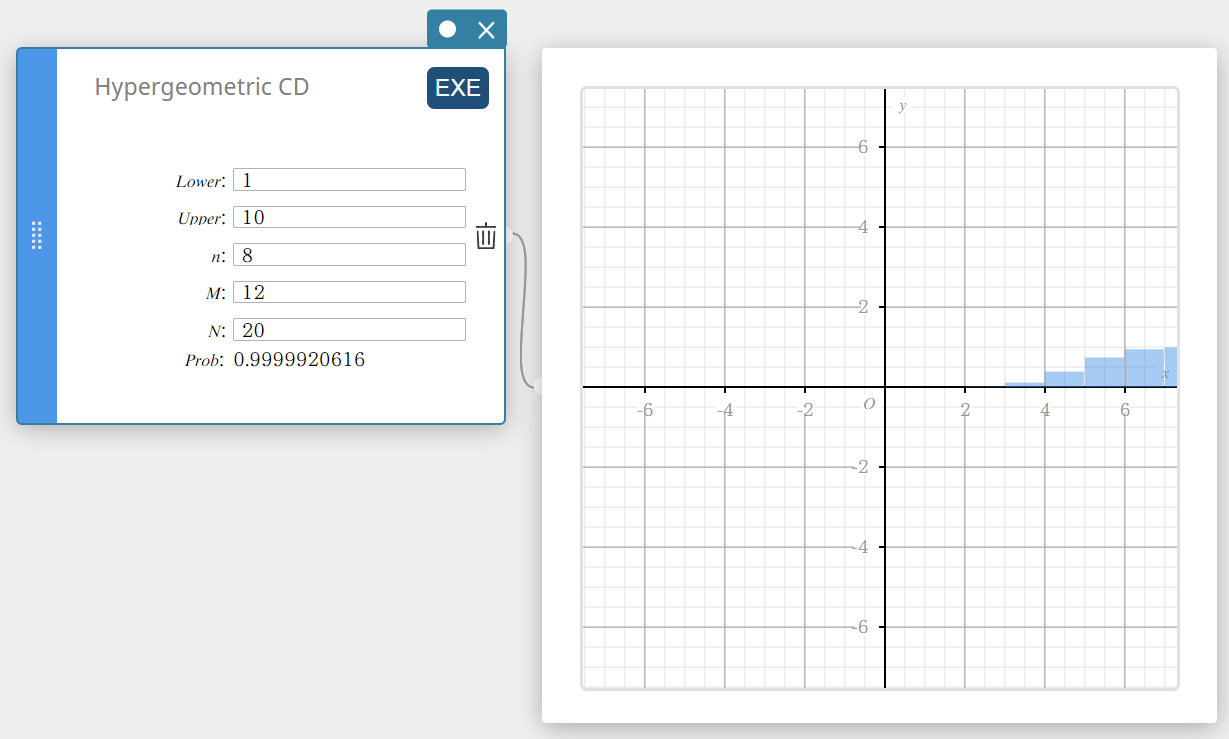
Hypergeometrische CD (Hypergeometrische cumulatieve verdeling)
Dit berekent de cumulatieve kans in een hypergeometrische verdeling dat er succes zal zijn bij of vóór een specifieke proef.

\( prob = \sum_{i=Lower}^{Upper}\displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

• Invoertermen
  Lower : onderste grens
  Upper : bovenste grens
  \(n\) : aantal proeven van populatie (0 \(≤\) n geheel getal)
  \(M\) : aantal successen in populatie (0 \(≤\) M geheel getal)
  \(N\) : grootte van populatie ( n \(≤\) N , M \(≤\) N geheel getal)

• Uitvoertermen
  Prob : hypergeometrische cumulatieve waarschijnlijkheid

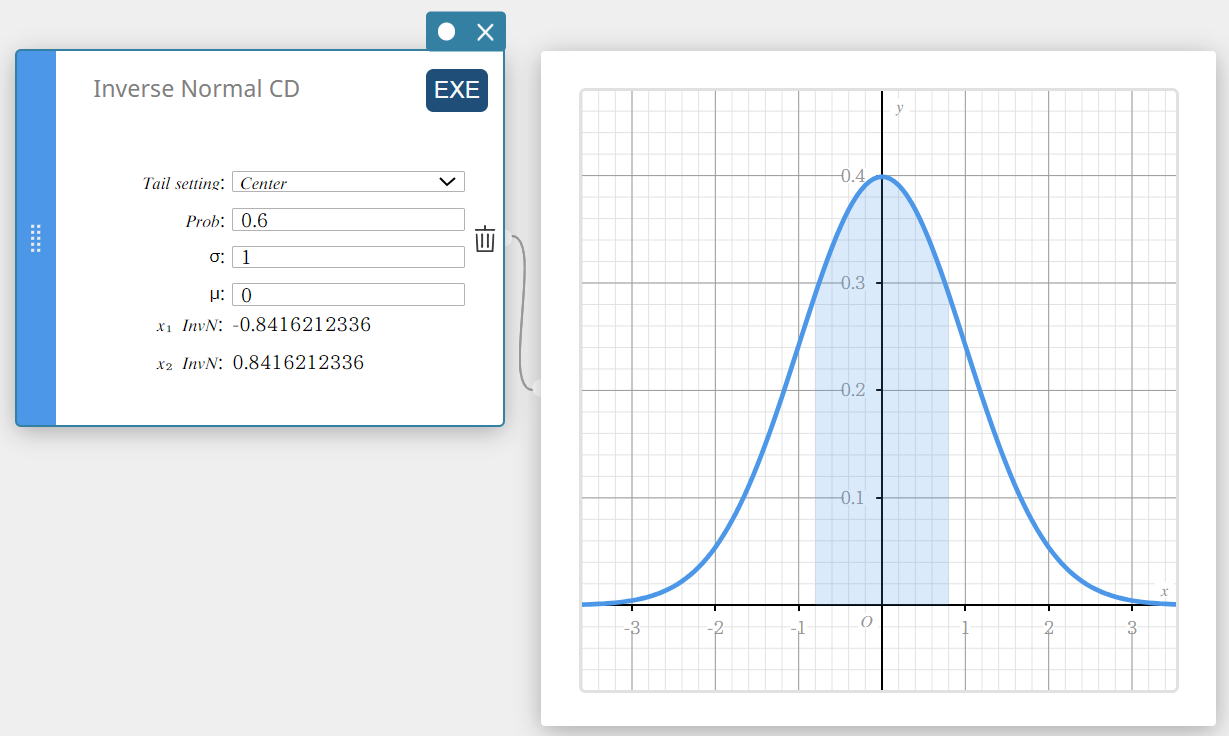
Inverse normale CD (Omgekeerde normale cumulatieve verdeling)
Dit berekent de grenswaarde(n) van een normale cumulatieve kansverdeling voor specifieke waarden.

Tail: Links
\( \int_{-\infty}^{\alpha}f(x)dx=p \)
Bovenste grens α wordt weergegeven.

Tail: Rechts
\( \int_{\alpha}^{+\infty}f(x)dx=p \)
Onderste grens α wordt weergegeven.

Tail: Midden
\( \int_{\alpha}^{\beta}f(x)dx=p \qquad \left( \mu=\displaystyle\frac{\alpha+\beta}{2} \right) \)
Onderste grens α en bovenste grens β worden weergegeven.

• Invoertermen
  Tail setting: tail-specificatie van kanswaarde (Center, Left, Right)
  Prob : waarschijnlijkheidswaarde (0 \(≤\) Area \(≤\) 1)
  \( \sigma \) : standaardafwijking populatie（\( \sigma > 0 \)）
  \( \mu \) : gemiddelde populatie

• Uitvoertermen
  \(x_1 {\rm InvN}\) : Bovengrens wanneer Tail: Links
       Ondergrens wanneer Tail: Rechts of Tail: Midden
  \(x_2 {\rm InvN}\) : Bovengrens wanneer Tail: Midden

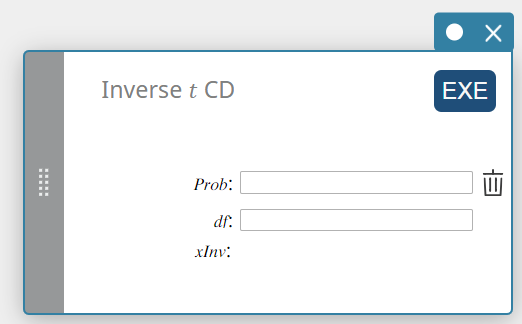
Inverse t CD (Omgekeerde t cumulatieve verdeling van een student)
Dit berekent de ondergrenswaarde van een t cumulatieve kansverdeling van een student voor specifieke waarden.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Invoertermen
  Prob : t cumulatieve waarschijnlijkheid (0 \(≤\) Area \(≤\) 1)
  \(df\) : vrijheidsgraden (df > 0)

• Uitvoertermen
  xInv: De ondergrenswaarde van een t cumulatieve kansverdeling van een student

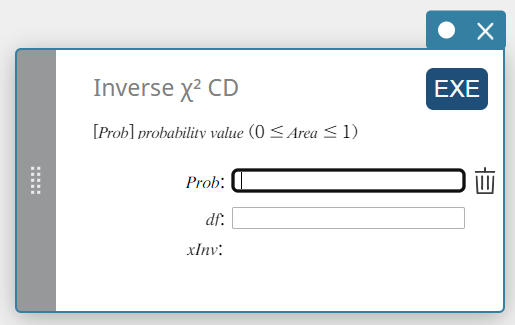
Omgekeerde \(\chi^2\) CD (Omgekeerde \(\chi^2\) cumulatieve verdeling)

Dit berekent de ondergrenswaarde van een \(\chi^2\) cumulatieve kansverdeling voor specifieke waarden.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Invoertermen
  Prob : \(\chi^2\) cumulatieve waarschijnlijkheid (0 \(≤\) Area \(≤\) 1)
  \(df\) : vrijheidsgraden (positief geheel getal)

• Uitvoertermen
  \(x {\rm Inv}\) : De ondergrenswaarde van een \(\chi^2\) cumulatieve kansverdeling

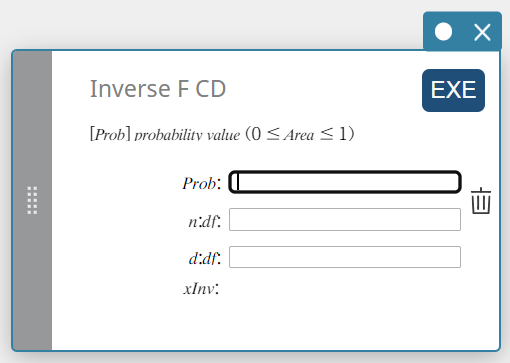
Omgekeerde F CD (Omgekeerde F cumulatieve verdeling)
Dit berekent de ondergrenswaarde van een F cumulatieve kansverdeling voor specifieke waarden.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Invoertermen
  Prob : F cumulatieve waarschijnlijkheid (0 \(≤\) Area \(≤\) 1)
  \(n:df\) : vrijheidsgraden van teller (positief geheel getal)
  \(d:df\) : vrijheidsgraden van noemer (positief geheel getal)

• Uitvoertermen
  xInv: De ondergrenswaarde van een F cumulatieve kansverdeling

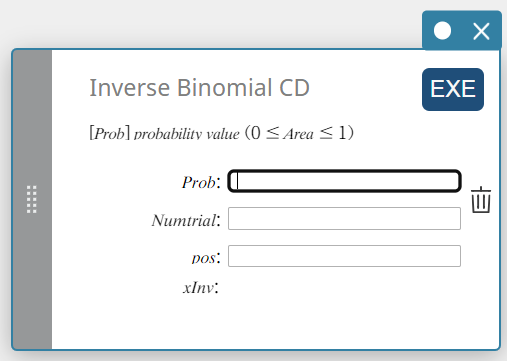
Inverse binomiale CD (Omgekeerde binomiale cumulatieve verdeling)
Dit berekent het minimale aantal proeven van een binomiale cumulatieve kansverdeling voor specifieke waarden.

\( \sum_{x=0}^{m}f(x)\ge prob \)

• Invoertermen
  Prob : binomiale cumulatieve waarschijnlijkheid（\(0 \le\) Area \(\le 1\)）
  Numtrial : aantal proeven n (geheel getal, n \(≥\) 0)
  pos : kans op succes p (0 \(≤\) p \(≤\) 1)

• Uitvoertermen
  xInv : De ondergrenswaarde van een F cumulatieve kansverdeling

Inverse Poisson CD (Omgekeerde Poisson cumulatieve verdeling)
Dit berekent het minimale aantal proeven van een Poisson cumulatieve kansverdeling voor specifieke waarden.

\( \sum_{x=0}^{m}f(x)\ge prob \)

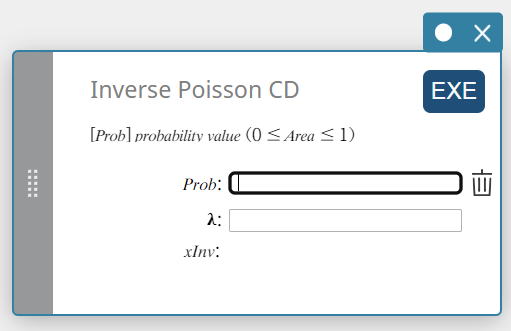
• Invoertermen
  Prob : Poisson cumulatieve waarschijnlijkheid（\(0 \le\) Area \(\le 1\)）
  \( \lambda \) : gemiddelde（\(\lambda \gt 0\)）

• Uitvoertermen
  xInv : Het minimale aantal proeven (de bovengrenswaarde) van een Poisson cumulatieve kansverdeling

Inverse Geo CD (Omgekeerde geometrische cumulatieve verdeling)
Dit berekent het minimale aantal proeven van een geometrische cumulatieve kansverdeling voor specifieke waarden.

\( \sum_{x=0}^{m}f(x)\ge prob \)

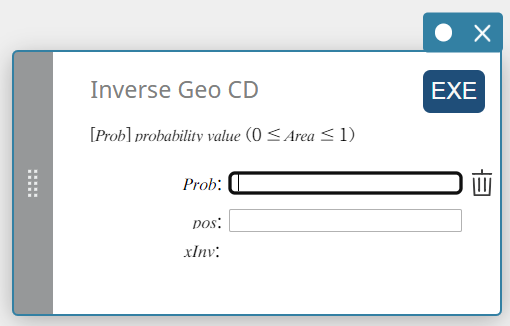
• Invoertermen
  Prob : geometrische cumulatieve waarschijnlijkheid（\(0 \le\) Area \(\le 1\)）
  pos : kans op succes p（\(0 \le p \le 1\)）

• Uitvoertermen
  xInv : Het minimale aantal proeven (de bovengrenswaarde) van een geometrische cumulatieve kansverdeling

Inverse hypergeometrisch (Omgekeerde hypergeometrische cumulatieve verdeling)
Dit berekent het minimale aantal proeven van een hypergeometrische cumulatieve kansverdeling voor specifieke waarden.

\( prob \le \sum_{i=0}^{X} \displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

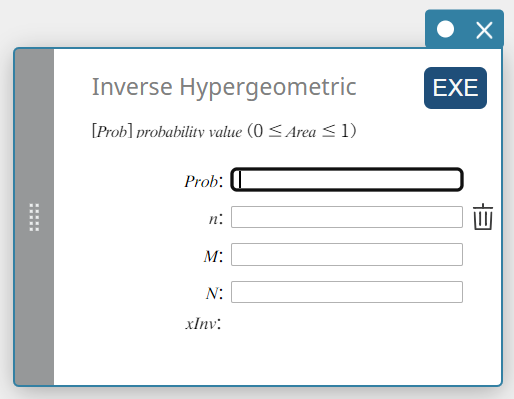
• Invoertermen
  Prob : hypergeometrische cumulatieve waarschijnlijkheid（\(0 \le\) Area \(\le 1\)）
  \(n\) : aantal proeven van populatie (0 \(≤\) n geheel getal)
  \(M\) : aantal successen in populatie (0 \(≤\) M geheel getal)
  \(N\) : grootte van populatie ( n \(≤\) N , M \(≤\) N geheel getal)

• Uitvoertermen
  xInv: Het minimale aantal proeven (de bovengrenswaarde) van een hypergeometrische cumulatieve kansverdeling

Andere statistische grafieken

Spreidingsdiagram
Van elke waarde wordt de cumulatieve z-score ten opzichte van de normale kansverdeling berekend en getekend. Als het spreidingsdiagram een rechte lijn sterk benadert, zijn de gegevens ongeveer normaal. Een afwijking van de rechte lijn wijst op een afwijking van normaliteit.

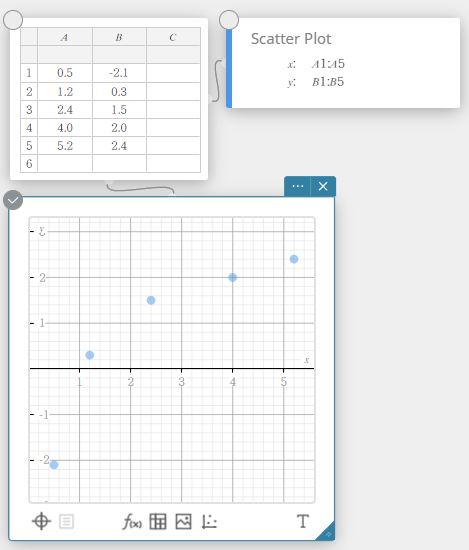
Box-en-whiskerplot
Met dit type grafiek kunt u een grote hoeveelheid gegevensitems groeperen in specifieke bereiken. De box stelt het eerste (\({\rm Q}_1\)) tot het derde kwartiel (\({\rm Q}_3\)) van alle gegevens voor, met een lijn op de mediaan (\({\rm Med}\)). Lijnen (zogeheten whiskers) lopen van het ene uiteinde van de box tot het minimum (\({\rm minX}\)) en maximum (\({\rm maxX}\)) van de gegevens.

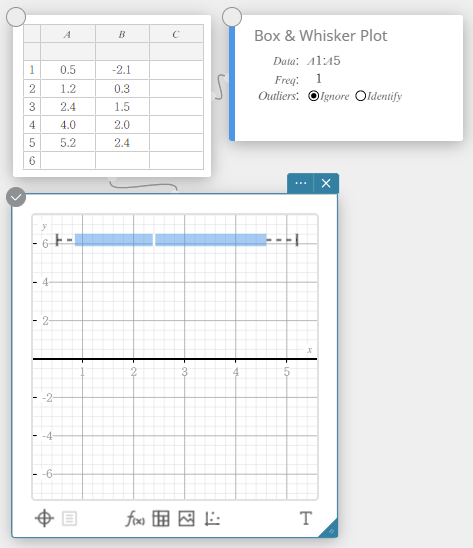
Histogram
Een histogram toont de frequentie (frequentieverdeling) van elke gegevensklasse als een rechthoekige balk. De klassen staan op de horizontale as en de frequentie op de verticale as. U kunt de startwaarde (\(H-Start\)) en stapwaarde (\(H-Step\)) van het histogram desgewenst wijzigen.

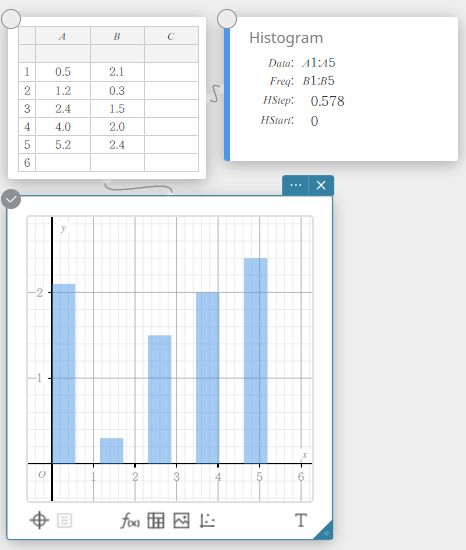
Cirkeldiagram
U kunt een cirkeldiagram tekenen op basis van gegevens in een specifieke lijst.

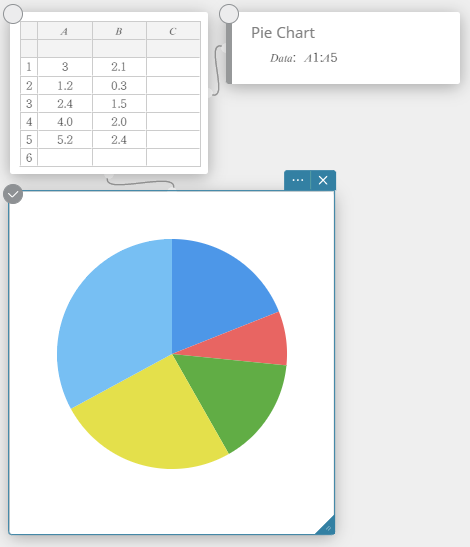
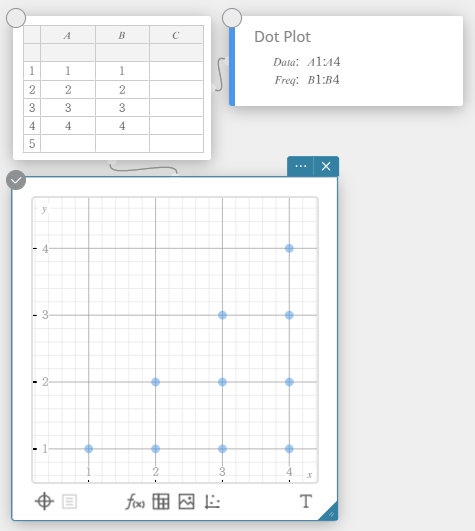
Puntendiagram
De waarden in kolom A (horizontale as) stellen bin-nummers voor, terwijl de waarden in kolom B (verticale as) het aantal gegevenspunten in elke bin voorstellen. Voor elk gegevenspunt in een bin wordt een punt uitgezet.