solve 
方程式または不等式の解を返します。
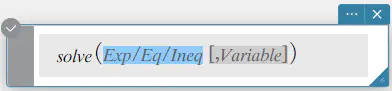
構文 1: solve(Exp/Eq/Ineq [, 変数] [ ) ]
- “[, 変数]” の部分を省略した場合の初期値は “\(x\)” です。
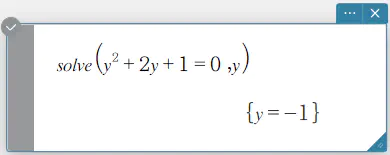
構文 2: solve(Exp/Eq/Ineq\(≠\), 変数[, 初期推定値, 下限, 上限] [ ) ]
- 初期推定値、下限、上限を含めた場合は、方程式または \(≠\) の式のみで有効です。この場合は、近似値が返されます。
- 初期推定値、下限、上限を省略した場合は、真の値が返されます。ただし、真の値が得られない場合は、初期推定値 \(=0\)、下限 \(=–\infty\)、上限 \(=\infty\) と仮定しての近似値が返されます。


構文 3: solve({Exp-1/Eq-1, …, Exp-N/Eq-N}, {変数-1, …, 変数-N} [ ) ]
- “Exp” が第 1 引数の場合は、Exp = 0 の方程式とみなされます。

構文 4: solve( コマンド内にベクトル方程式を入力した場合は、2つのオブジェクト(点、直線、平面、または球)の関係を解くことができます。ここでは、solve( コマンドを使ってベクトル方程式を解くための、4つの典型的な構文を示します。
下記構文では、Vct-1 から Vct-6 までは 3つ(または 2つ)の要素を持つ列ベクトルを表し、s, t, u, v はパラメーターを表します。
solve(Vct-1 + s * Vct-2 [= Vct-3, {変数-1}])
- 上記の構文で方程式の右辺(= Vct-3)が省略された場合に、右辺のすべての要素は 0 ベクトルとみなされます。
solve(Vct-1 + s * Vct-2 = Vct-3 + t* Vct-4, {変数-1, 変数-2})
solve(Vct-1 + s * Vct-2 + t* Vct-3 = Vct-4 – u * Vct-5, {変数-1, 変数-2, 変数-3})
solve(Vct-1 + s* Vct-2 + t * Vct-3 = Vct-4 – u* Vct-5 + v * Vct-6, {変数-1, 変数-2, 変数-3, 変数-4}) -
上記 4つの構文においては、変数(変数 1 から変数 4 )を各ベクトル(Vct-1 から Vct-6)の要素に入力して、それらの変数について解くことができます。

dSolve 
1 次、2 次、3 次の常微分方程式、または線形微分方程式系を解きます。
構文: dSolve(Eq, 独立変数, 従属変数 [, 初期条件-1, 初期条件-2][, 初期条件-3, 初期条件-4][, 初期条件-5, 初期条件-6] [ ) ]
dSolve({Eq-1, Eq-2}, 独立変数, {従属変数-1, 従属変数-2} [, 初期条件-1, 初期条件-2, 初期条件-3, 初期条件-4] [ ) ]
- 初期条件を省略した場合に、解は任意定数を含みます。
- Var = Exp の構文を使って、すべての初期条件を入力します。その他の構文を使った初期条件は、無視されます。


taylor 
指定した変数に関する式の、テイラー多項式を求めます。
構文: taylor (Exp/List, 変数, 次数 [, 中心点] [ ) ]
- “[, 中心点]” を省略した場合の初期値は 0 です。

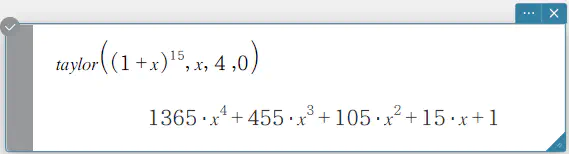
laplace, invLaplace 
“laplace” はラプラス変換のコマンド、“invLaplace” は逆ラプラス変換のコマンドです。
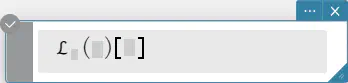
構文: laplace \(\mathcal{L}_t (f(t))[s]\)
\(f(t)\): 式
\(t\):変数(この変数に関して式が変換されます)
\(s\): 変換パラメーター
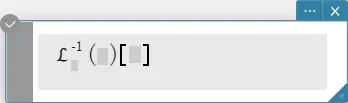
invLaplace \(\mathcal{L}_s^{-1} (L(s))[t]\)
\(L(s)\): 式
\(s\): 変数(この変数に関して式が変換されます)
\(t\): 変換パラメーター
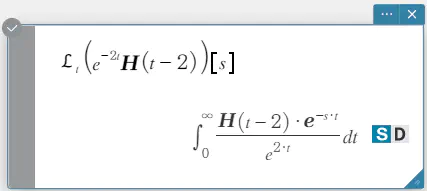
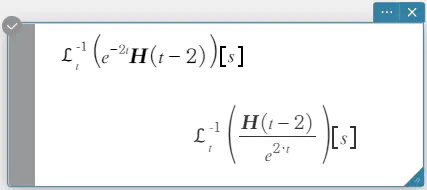
fourier, invFourier 
“fourier” はフーリエ変換のコマンド、“invFourier” は逆フーリエ変換のコマンドです。
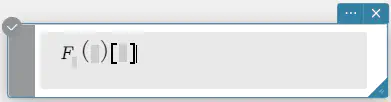
構文: fourier \(~ Ϝ_x (f(x))[w]\)
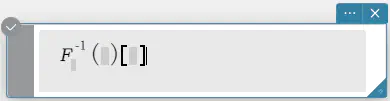
invFourier \(~ Ϝ_w^{-1} (f(w))[x]\)
\(x\): 変数(この変数に関して式が変換されます)
\(w\): 変換パラメーター
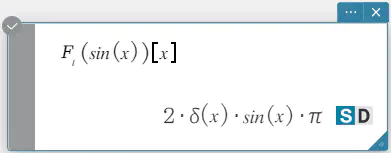

FFT, IFFT 
“FFT” は高速フーリエ変換のコマンド、“IFFT” は逆高速フーリエ変換のコマンドです。
FFT および IFFT を実行するには、\(2^n\) データ値が必要です。FFT および IFFT は、数値的に計算されます。
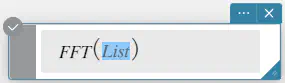
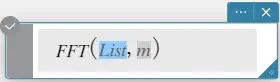
構文: FFT(list) または FFT(list, m)
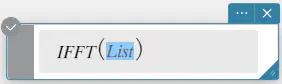
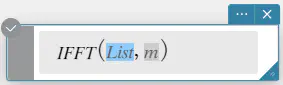
IFFT(list) または IFFT(list, m)
- n = 1, 2, 3, … の場合に、データサイズは \(2^n\) である必要があります。
- m はオプションです。FFT パラメーターを 0(信号処理)、1(純粋数学)、2(データ分析)のいずれかから指定します。