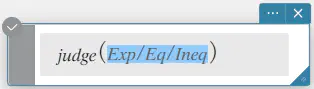
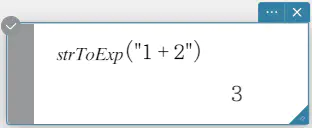judge
式が真の場合は TRUE を返し、偽の場合は FALSE を返します。

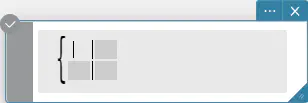
piecewise
条件式が真の場合は 1つの値を返し、偽の場合は別の値を返します。
構文:
\(\begin{cases} \lt \text{真の場合の戻り値} \gt | \lt \text{条件式} \gt \cr
\lt \text{偽または不定の場合の戻り値} \gt \end{cases}\)
または
\(\begin{cases} \lt \text{条件式 1 が真の場合の戻り値} \gt | \lt \text{条件式 1}
\gt \cr \lt \text{条件式 2 が真の場合の戻り値} \gt | \lt \text{条件式 2}
\gt \end{cases}\)

isPrime
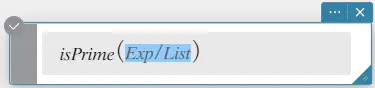
引数として指定された数値が素数かどうかを判定します。引数が素数のときは TRUE、素数でないときは FALSE を返します。
構文: isPrime(Exp/List[ ) ] (Exp、および List のすべての要素は整数)

|(代入演算子)
変数に対して一時的に値を割り当てます。この演算子は次のように使います。
- | の左側に置いた変数に、| の右側に置いた値を割り当てる
- | の左側に置いた変数の範囲を、| の右側に置いた条件によって制限する
構文: Exp/Eq/Ineq/List/Mat | Eq/Ineq/List/( “and” 演算子)
この演算子の右側には、複数の条件を、リスト形式、または “and” 演算子で接続することにより、指定することができます。また、この演算子の左側、右側のどちらでも、“\(\small{\neq}\)” を使うことができます。
MEMO
| は【数学記号】キーボードを使って入力します。
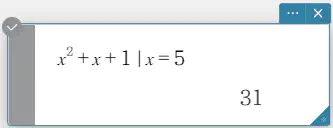
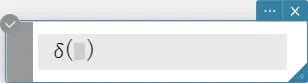
delta 
ディラックのデルタ関数です。この関数は、下記に示すように数値的に評価されます。
\( \delta(x) = \begin{cases} 0,~ x \neq 0 \cr \delta(x),~ x=0 \end{cases} \)
\(x\): 変数または数値

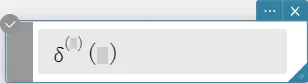
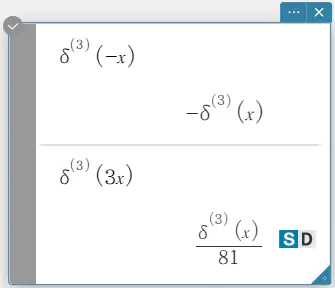
\(n\)th-delta 
ディラックのデルタ関数の n 次微分です。
構文: \( δ^{(n)} (x) \)
\(x\) : 変数または数値
\(n\) : 微分回数
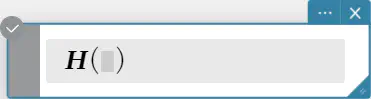
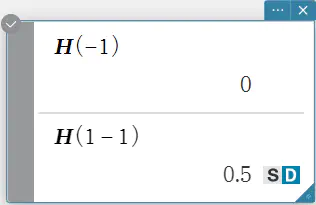
heaviside
ヘヴィサイド関数のコマンドであり、下記に示すように数値式のみを評価します。
\(H(x) = \begin{cases} 0,~ x \lt 0 \cr \frac 12,~ x = 0 \cr 1,~ x \gt 0 \end{cases}\)
\(x\): 変数または数値
gamma 
ガンマ関数のコマンドです。
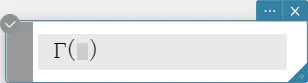
構文: \(\displaystyle \Gamma (x) = \int_0^{+\infty} t^{x-1} e^{-t} dt\)
\(x\): 変数または数値

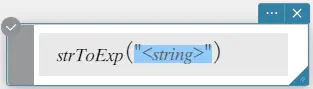
strToExp
文字列を式に変換し、その式を実行します。
構文: strToExp (“<文字列>”)