このページの目次
統計計算の基本操作
統計データを編集する
統計計算に使うデータを選択する
1変数統計計算を実行する
計算結果をコピーする
回帰グラフを描画する
ヒストグラムを描画する
箱ひげ図を描画する
円グラフを描画する
散布図の操作
1標本Z検定を実行する
統計計算と統計グラフ
統計計算の基本操作
- 統計データスティッキーへ値を入力するには
ここでは例として、下表のデータ値を統計データスティッキーのセル A1~B5 に入力します。
| A | B | |
|---|---|---|
| 1 | \(0.5\) | \(-2.1\) |
| 2 | \(1.2\) | \(0.3\) |
| 3 | \(2.4\) | \(1.5\) |
| 4 | \(4.0\) | \(2.0\) |
| 5 | \(5.2\) | \(2.4\) |
- スティッキーメニューの
 をクリックする。
をクリックする。

統計データスティッキーが作成されます。
セル A1 にカーソルが表示されます。 - \(0.5\) と入力し、「Enter」キーを押す。
セル A2 が選択状態になります。 - \(1.2\) と入力し、「Enter」キーを押す。
セル A3 が選択状態になります。以下同様に、セル A5 まで入力します。 - セル B1 をクリックする。
セル B1 が選択状態になります。 - \(-2.1\) と入力し、「Enter」キーを押す。
セル B2 が選択状態になります。このとき、C列が作成されます(下記のMEMOを参照)。 - \(0.3\) と入力し、「Enter」キーを押す。
セル B3 が選択状態になります。以下同様に、セル B5 まで入力します。
MEMO
最も右側の列へはじめて値を入力した場合に、列の右側に列が追加されます。
列ラベル(A, B, C, …)直下のセルは、各列をリストデータとして使うための、リスト名の入力欄です。詳しくは、「リストに名前を付けるには」を参照してください。
- 統計計算に使うデータ値を選択するには
- 「統計データスティッキーへ値を入力するには」の操作で、下表のデータ値を入力する。
A B 1 \(0.5\) \(-2.1\) 2 \(1.2\) \(0.3\) 3 \(2.4\) \(1.5\) 4 \(4.0\) \(2.0\) 5 \(5.2\) \(2.4\) - セル A1 ~セル B5 の範囲をドラッグする。
セル A1 ~セル B5 の範囲が選択されます。
MEMO
列番号をクリックすると、クリックした列すべてを選択することができます。
列番号をドラッグすると、ドラッグした列すべてを選択することができます。
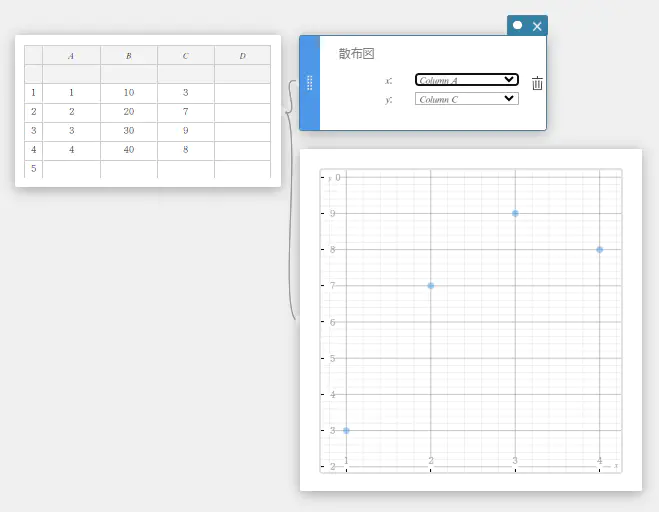
クリックまたはドラッグして選択した列番号のデータを使って、グラフを描画できます。
この場合、描画後でもグラフスティッキーのドロップダウンリストを使って、別の列番号を選択し直すことが可能です。
- 統計計算を実行するには
ここでは例として 2変数統計計算を実行し、散布図と 1次回帰グラフを描画します。
- 下表のデータ値を入力し、入力したデータをすべて選択する。
A B 1 \(0.5\) \(-2.1\) 2 \(1.2\) \(0.3\) 3 \(2.4\) \(1.5\) 4 \(4.0\) \(2.0\) 5 \(5.2\) \(2.4\) 
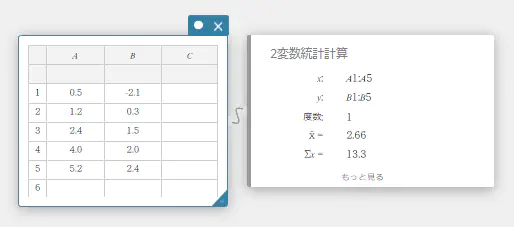
- ソフトキーボードの【計算】-【2変数統計計算】を順にクリックする。

2変数統計計算スティッキーが表示されます。
- ソフトキーボードの
 をクリックする。
をクリックする。

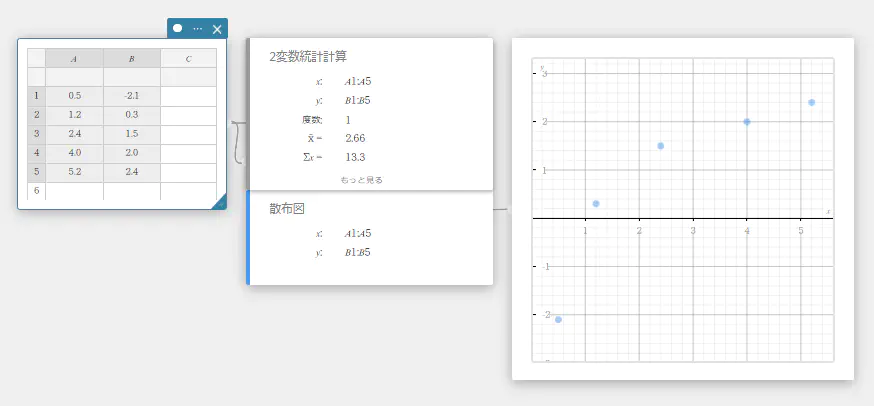
- ソフトキーボードの【グラフ】-【散布図】を順にクリックする。

散布図スティッキーと、散布図が描画されたグラフスティッキーが作成されます。
- ソフトキーボードの
 をクリックする。
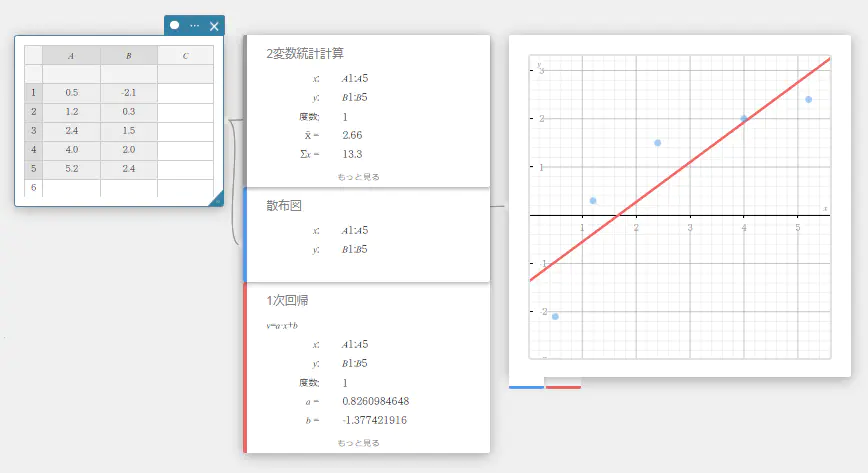
をクリックする。 - ソフトキーボードの【回帰】-【1次回帰】を順にクリックする。

1次回帰スティッキーが作成され、グラフスティッキーに 1次回帰グラフが描画されます。
- テンプレートを使って統計グラフを描画する
テンプレートを使うと、簡単な操作で統計グラフを描画できます。
ここでは例として正規確率密度演算のグラフを描画します。
- スティッキーメニューの
 をクリックする。
をクリックする。

統計計算スティッキーが表示されます。 - 【分布】を選択する。
- 【正規確率密度演算】を選択する。
正規確率密度演算のテンプレートが表示されます。 - 値を入力し【実行】を選択、または「Enter」キーを押す。
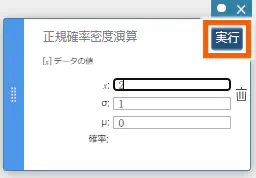
グラフが描画されます。
統計データを編集する
- データ値を修正するには
- 修正したいデータ値のセルをクリックする。
- 新しいデータ値を入力し、「Enter」を押す。

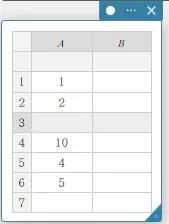
- 行を挿入するには
- 新しい行を挿入したい行の番号を右クリックする。
メニューが表示されます。
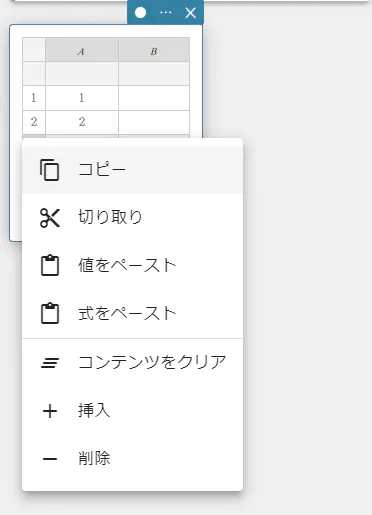
- 【挿入】をクリックする。
行が挿入されます。
- 列を挿入するには
- 新しい列を挿入したい列の番号を右クリックする。
メニューが表示されます。
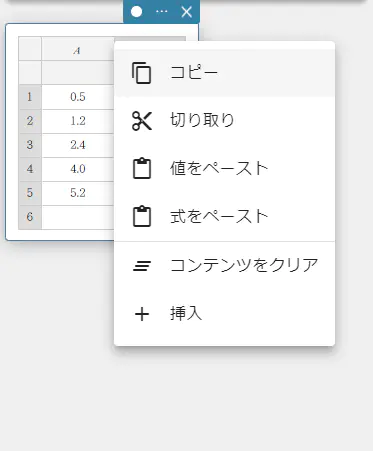
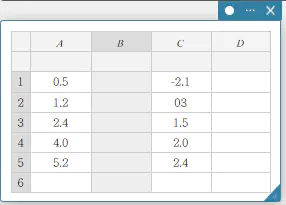
- 【挿入】をクリックする。
列が挿入されます。
- 行を削除するには
- 削除したい行の番号を右クリックする。
メニューが表示されます。
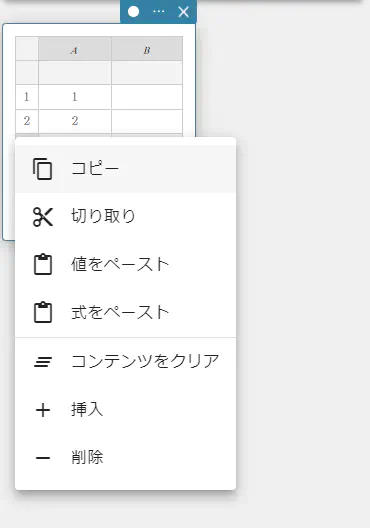
- 【削除】をクリックする。
行が削除されます。
- 列を削除するには
- 削除したい列の番号を右クリックする。
メニューが表示されます。
- 【削除】をクリックする。
列が削除されます。
- リストに名前を付けるには
リスト名を付けると、検定や他の統計計算をする際に、リスト名を使ってリストデータを呼び出すことができます。リスト名は、列ラベル(A, B, C, …)直下のセルに入力します。
例: 列A のリスト名を「List1」にするには
- 列ラベル「A」直下のセルをダブルクリックする。
カーソルが表示され、入力状態になります。
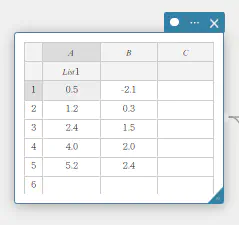
- 「List1」と入力し、「Enter」を押す。
A列のリスト名が「List1」になります。
MEMO
リスト名の入力時は、次の点にご注意ください。
- 8 文字以内で入力してください。
- 先頭の文字は、アルファベットにしてください。
- 英数字(大文字、小文字)や下付き文字を使うことができます。
- 大文字と小文字は、区別されます。例えば abc、Abc、aBc、ABC は、それぞれ異なるリスト名として扱われます。
統計計算に使うデータを選択する
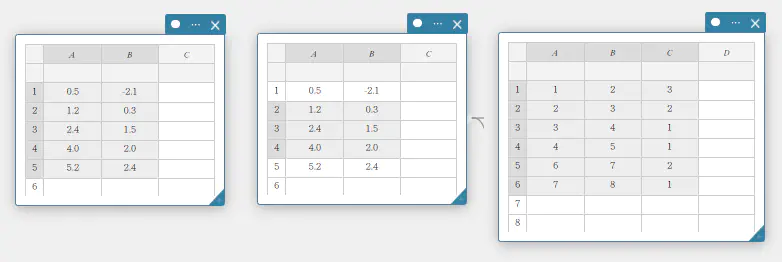
あるセルから別のセルへとマウスポインターをドラッグすることで、セルの範囲を選択することができます。
データ選択例
MEMO
列番号をクリックすると、クリックした列すべてを選択することができます。
列番号をドラッグすると、ドラッグした列すべてを選択することができます。
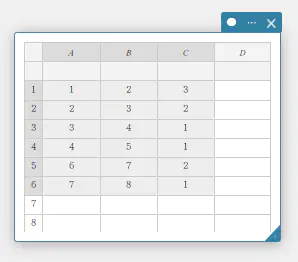
選択範囲に空欄のセルがある場合でも、統計計算は実行できます。
統計計算に使うことができる列数は、最大で3列までです。4列以上が選択されている場合、統計計算は実行することができません。
1変数統計計算を実行する
- 下表のデータ値のデータを A列、度数を B列に入力する。
データ 度数 \(1\) \(1\) \(2\) \(2\) \(3\) \(3\) \(4\) \(2\) \(5\) \(1\) - セル A1~B5 をドラッグして選択する。
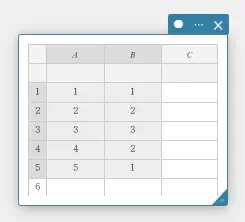
- ソフトキーボードの【計算】-【1変数統計計算】を順にクリックする。
1変数統計計算スティッキーが作成されます。
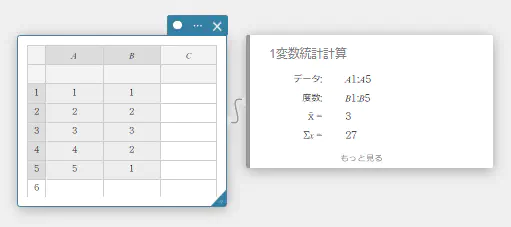
- 1変数統計計算スティッキーの【もっと見る】をクリックする。
隠れている計算結果が表示されます。
【折りたたむ】をクリックすると、隠れた状態に戻ります。
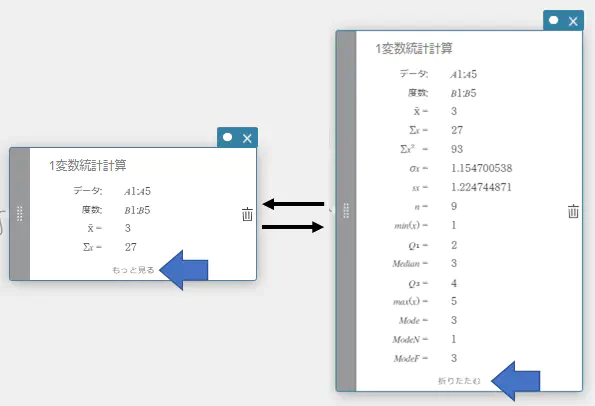
- 1変数統計計算を実行すると、下記の結果が表示されます。
\(\bar{\rm x}\) 平均値
\(\Sigma {\rm x}\) データの総和(合計値)
\(\Sigma {\rm x}^2\) データの二乗和(データを 2乗して合計した値)
\(\sigma {\rm x}\) データの母標準偏差
\({\rm sx}\) データの標本標準偏差
\({\rm n}\) データの数
\({\rm min(x)}\) データの最小値
\({\rm Q}_1\) データの第 1 四分位点(First Quartile)
\({\rm Med}\) データの中央値
\({\rm Q}_3\) データの第 3 四分位点(Third Quartile)
\({\rm max(x)}\) データの最大値
\({\rm Mode}\) データの最頻値
\({\rm ModeN}\) データの最頻値の個数
\({\rm ModeF}\) データの最頻値の度数
\({\rm Mode}\) が複数個の解を持つときは、それらすべてが表示されます。
計算結果をコピーする
統計計算の計算結果はコピーすることができます。
- コピーしたい計算結果にマウスカーソルを合わせる。
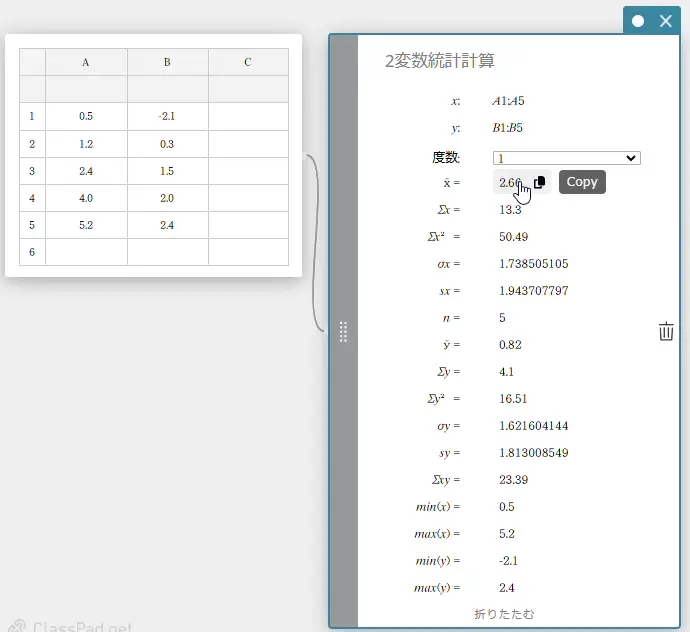
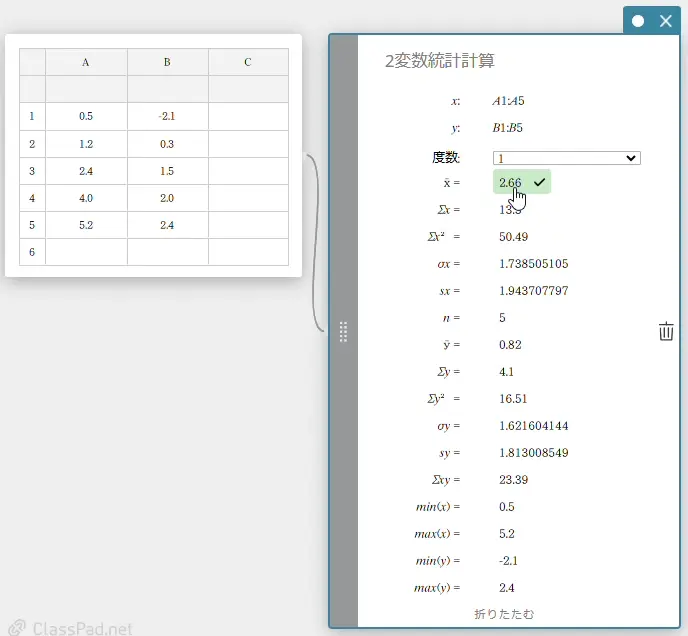
- マウスカーソルを合わせた計算結果をクリックする。
計算結果がコピーされます。
回帰グラフを描画する
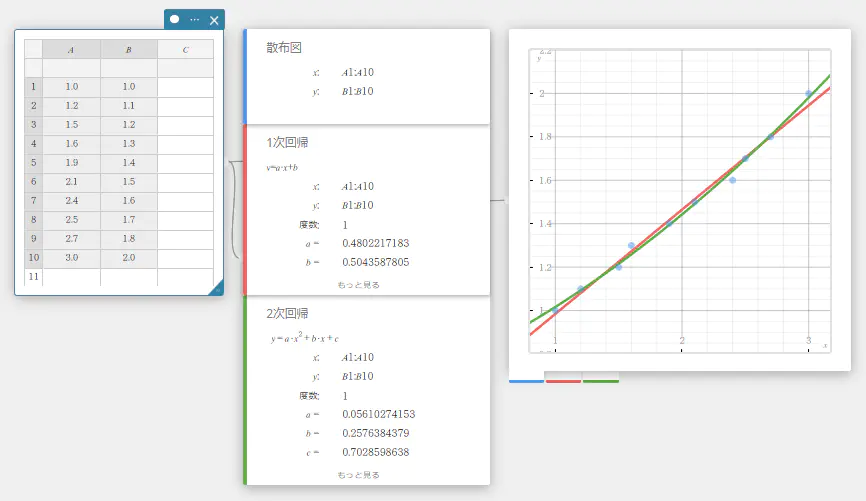
ここでは例として、散布図、1次回帰グラフ、および2次回帰グラフを描画します。
- 下表のデータ値を入力し、入力したデータをすべて選択する。
A B \(1.0\) \(1.0\) \(1.2\) \(1.1\) \(1.5\) \(1.2\) \(1.6\) \(1.3\) \(1.9\) \(1.4\) \(2.1\) \(1.5\) \(2.4\) \(1.6\) \(2.5\) \(1.7\) \(2.7\) \(1.8\) \(3.0\) \(2.0\) 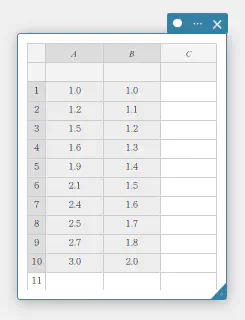
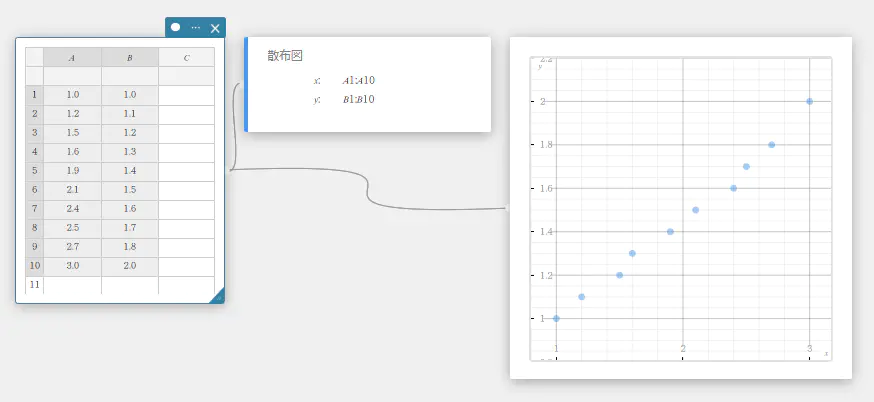
- ソフトキーボードの【グラフ】-【散布図】を順にクリックする。

散布図スティッキーと、散布図が描画されたグラフスティッキーが作成されます。
- ソフトキーボードの
 をクリックする。
をクリックする。
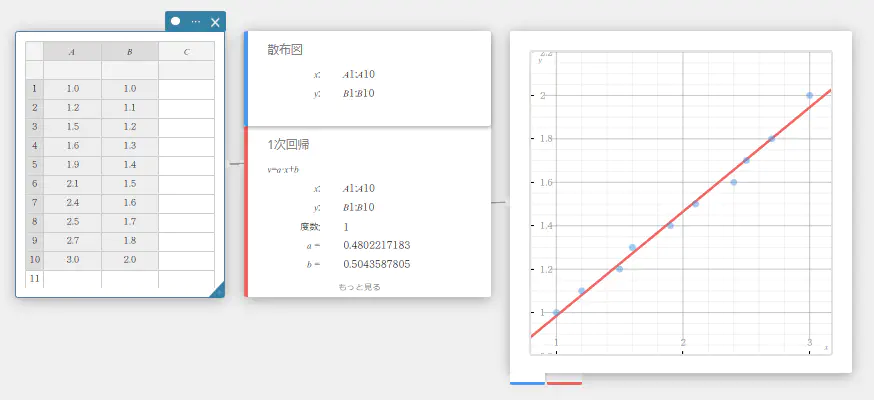
- ソフトキーボードの【回帰】-【1次回帰】を順にクリックする。

1次回帰スティッキーが作成され、グラフスティッキーに 1次回帰グラフが描画されます。
- ソフトキーボードの【2次回帰】をクリックする。

2次回帰スティッキーが作成され、グラフスティッキーに 2次回帰グラフが描画されます。
ヒストグラムを描画する
- 下表のデータ値のデータを A列、度数を B列に入力する。
データ 度数 \(1\) \(1\) \(2\) \(2\) \(3\) \(3\) \(4\) \(2\) \(5\) \(1\) - セル A1~B5 をドラッグして選択する。
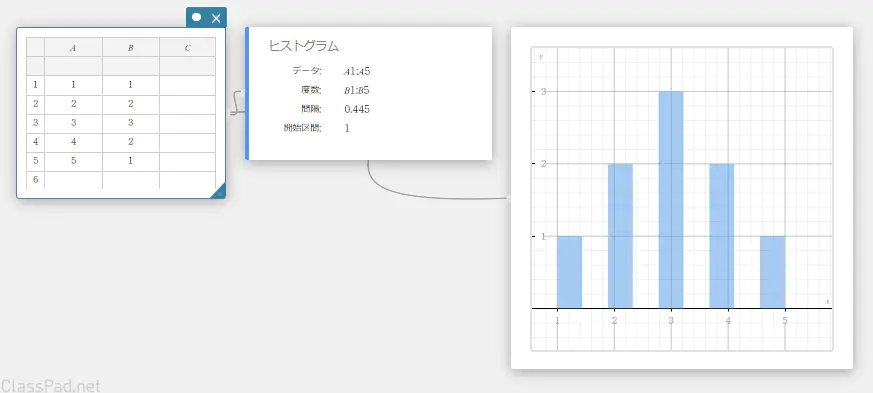
- ソフトキーボードの【グラフ】-【ヒストグラム】を順にクリックする。
ヒストグラムスティッキーとグラフスティッキーが作成され、グラフスティッキーにヒストグラムが描画されます。
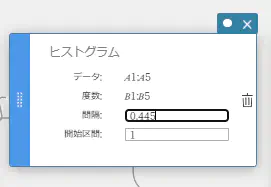
MEMO
ヒストグラムスティッキーの開始区間と間隔をクリックすると、ヒストグラムの開始値(開始区間)とステップ値(間隔)を変更することができます。
箱ひげ図を描画する
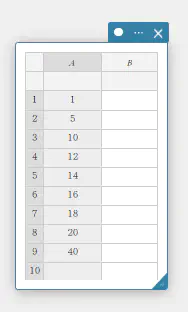
- 下表のデータ値をA列に入力する。
A \(1\) \(5\) \(10\) \(12\) \(14\) \(16\) \(18\) \(20\) \(40\) - セル A1~A9 をドラッグして選択する。
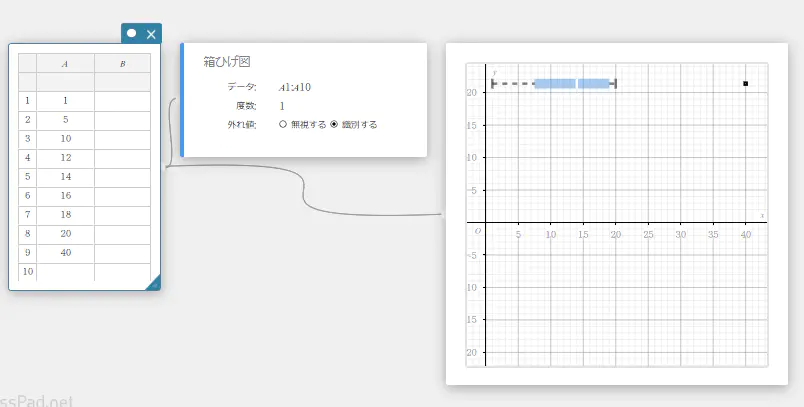
- ソフトキーボードの【グラフ】-【箱ひげ図】を順にクリックする。
箱ひげ図スティッキーとグラフスティッキーが作成され、グラフスティッキーに箱ひげ図が描画されます。
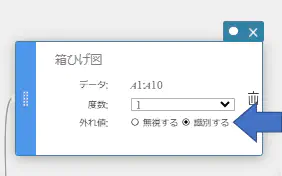
MEMO
箱ひげ図スティッキーの外れ値で【識別する】を選択すると、外れ値を表示することができます。
円グラフを描画する
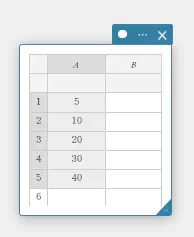
- 下表のデータ値のデータをA列に入力する。
A \(5\) \(10\) \(20\) \(30\) \(40\) - セル A1~A5 をドラッグして選択する。
- ソフトキーボードの【グラフ】-【円グラフ】を順にクリックする。
円グラフスティッキーが作成されると同時に、別のスティッキー(※)に円グラフが描画されます。
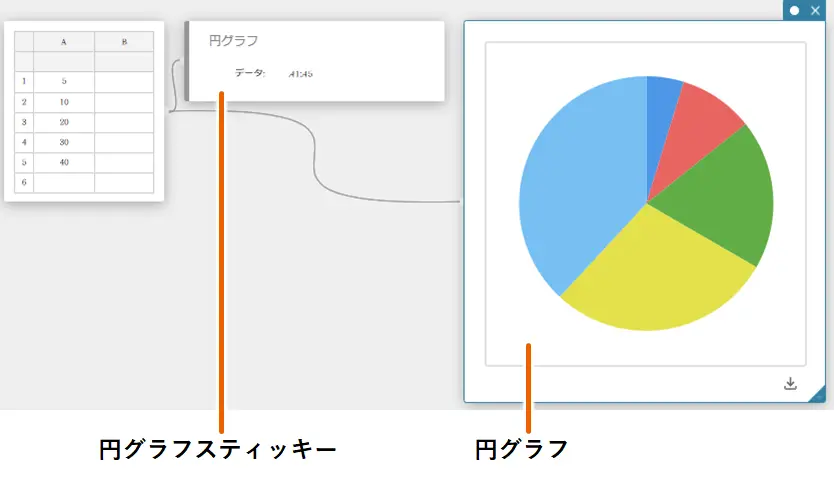
※グラフは通常グラフスティッキーに描画されますが、円グラフが描画されるスティッキーのみ、タイプが異なります。
MEMO
円グラフの をクリックすると、円グラフを画像でダウンロードすることができます。
をクリックすると、円グラフを画像でダウンロードすることができます。
散布図の操作
- 散布図上の点を動かすには
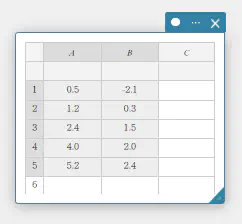
- 下表のデータ値を A列、B列に入力する。
データ 度数 \(0.5\) \(-2.1\) \(1.2\) \(0.3\) \(2.4\) \(1.5\) \(4.0\) \(2.0\) \(5.2\) \(2.4\) - セル A1~B5 を、ドラッグして選択する。
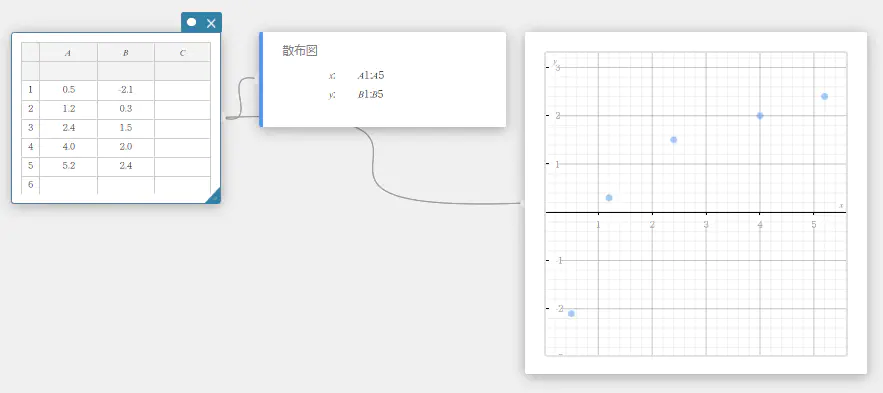
- ソフトキーボードの【グラフ】-【散布図】を順にクリックする。
散布図スティッキーとグラフスティッキーが作成され、グラフスティッキーに散布図が描画されます。
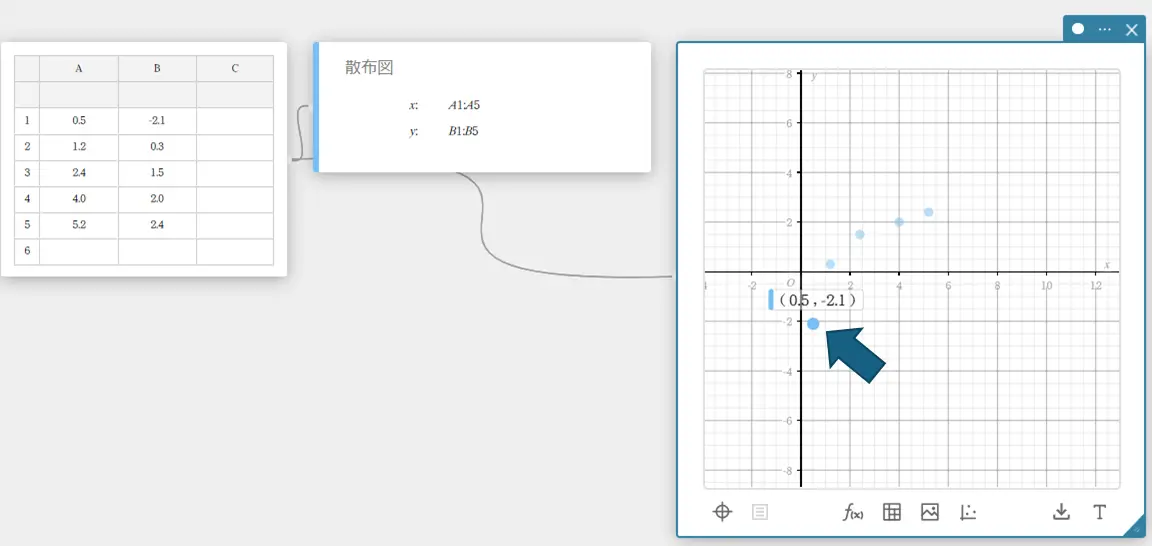
- 散布図上の点をドラッグする。
散布図の点が移動し、統計データスティッキーの値も、移動に従って更新されます。
- セルをロックするには
MEMO
セルをロックした場合に、散布図の点は座標が固定されます。例えば、A列のセルをロックした場合は、散布図の点が X軸方向へ移動することができなくなります。
- 「散布図上の点を動かすには」の操作に続いて、セル A1 を選択する。
- 統計計算スティッキーの
 をクリックする。
をクリックする。
- 「セルをロック」の横の
 をクリックする。
をクリックする。
セル A1 がロックされます。散布図のセル A1 • B1 に該当する点をドラッグしても、X軸方向に移動することはできません。
- セルをアンロックするには
- ロックされているセルを選択する。
- 統計計算スティッキーの (
 ) をクリックする。
) をクリックする。
- 「セルをアンロック」の横の
 をクリックする。
をクリックする。
1標本Z検定を実行する
- 標本データ数を指定して1標本Z検定を実行するには

例:
標本データ数: \(n=48\)
標本平均値: \(\overline{x}=24.5\)
帰無仮説: \(\mu \ne 0\)
母標準偏差: \(\sigma=3\)
- 統計計算スティッキーを作成する。
- ソフトキーボードの【検定】-【1標本Z検定】の順にクリックする。

1標本Z検定スティッキーが作成されます。
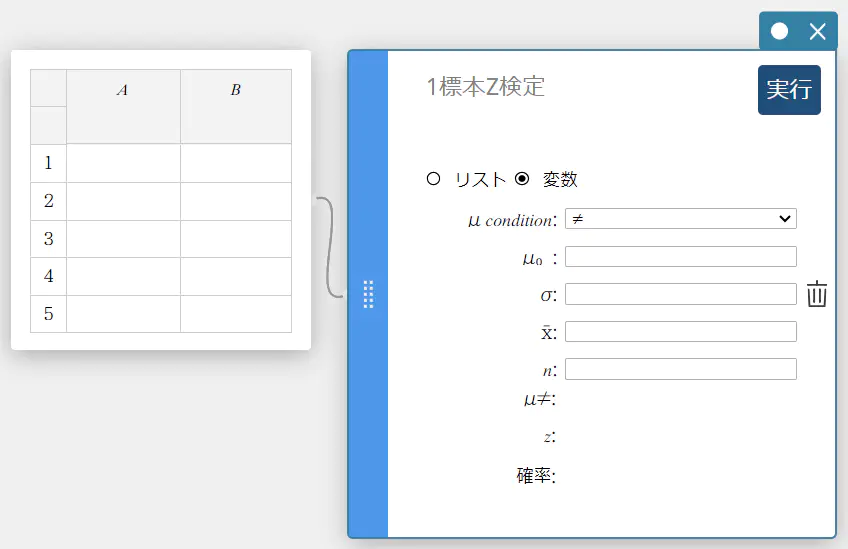
- 各項目に下記の値を入力する。
\(\mu\) condition: メニューから【\(\ne\)】を選択
\(\mu_0\) : \(0\)
\(\sigma\): \(3\)
\(\overline{x}\) : \(24.5\)
\(n\) : \(48\)
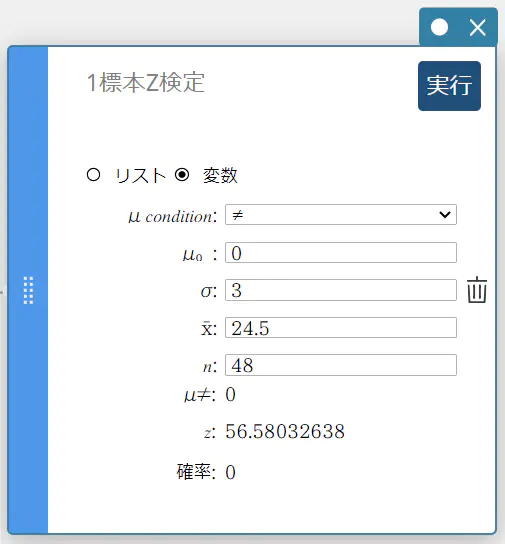
- 【実行】をクリックする。
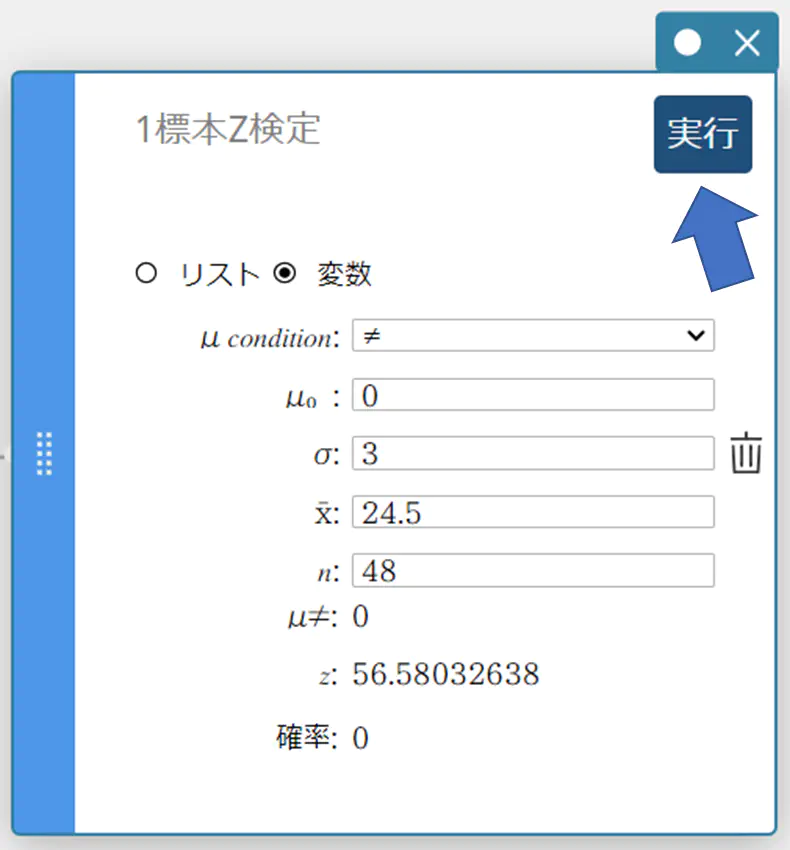
計算結果が表示され、グラフスティッキーにグラフが描画されます。
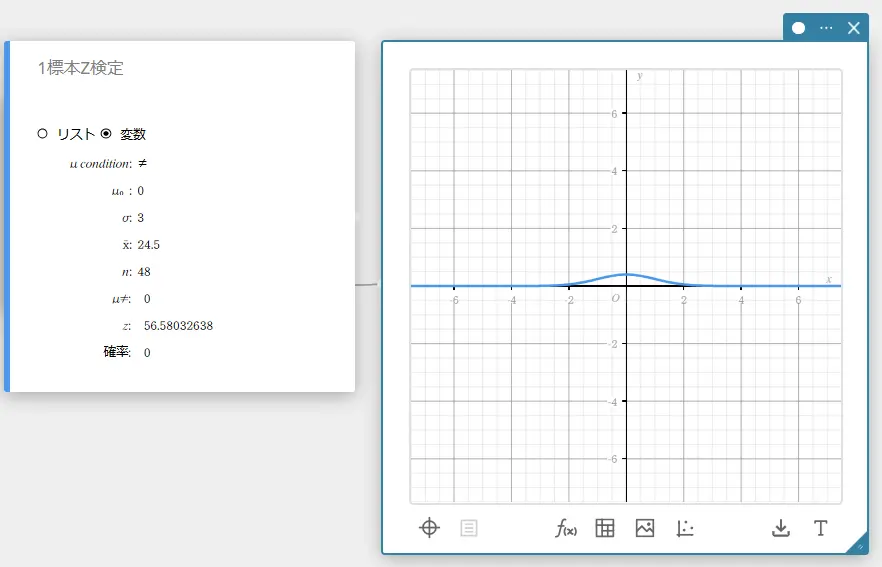
\(\mu \ne\) 母平均条件
\(\rm z\) \(\rm z\) 値
確率 \(\rm p\) 値
\(\overline{x}\) 標本平均値
\(n\) 標本データ数
- リストを使って1標本Z検定を実行するには

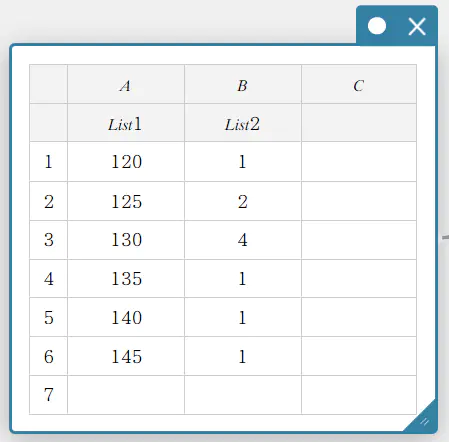
- A列に List1、B列に List2 とリスト名を入力する。
- 下表のデータ値を入力する。
- セル A1~B6 をドラッグして選択する。
- ソフトキーボードの【検定】-【1標本Z検定】の順にクリックする。

1標本Z検定スティッキーが作成されます。
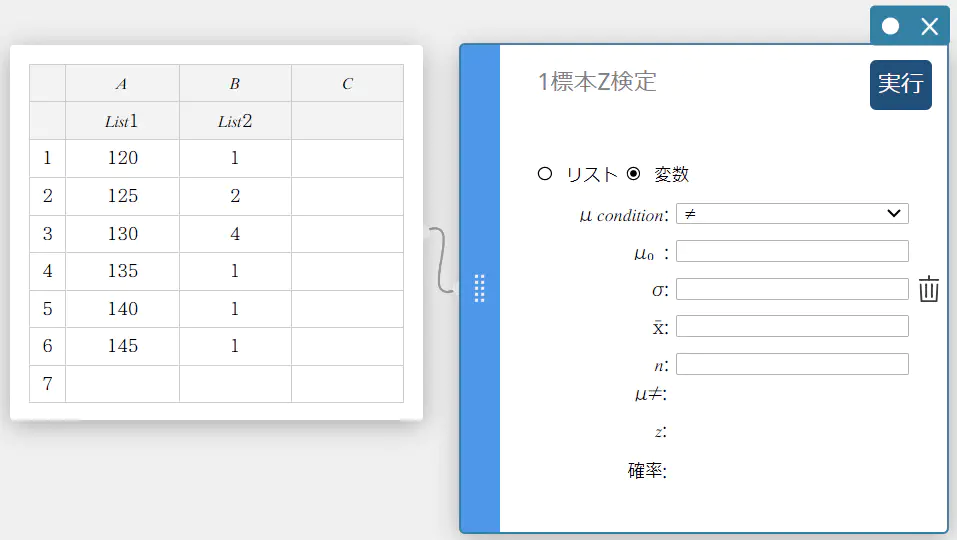
- 【リスト】をクリックする。
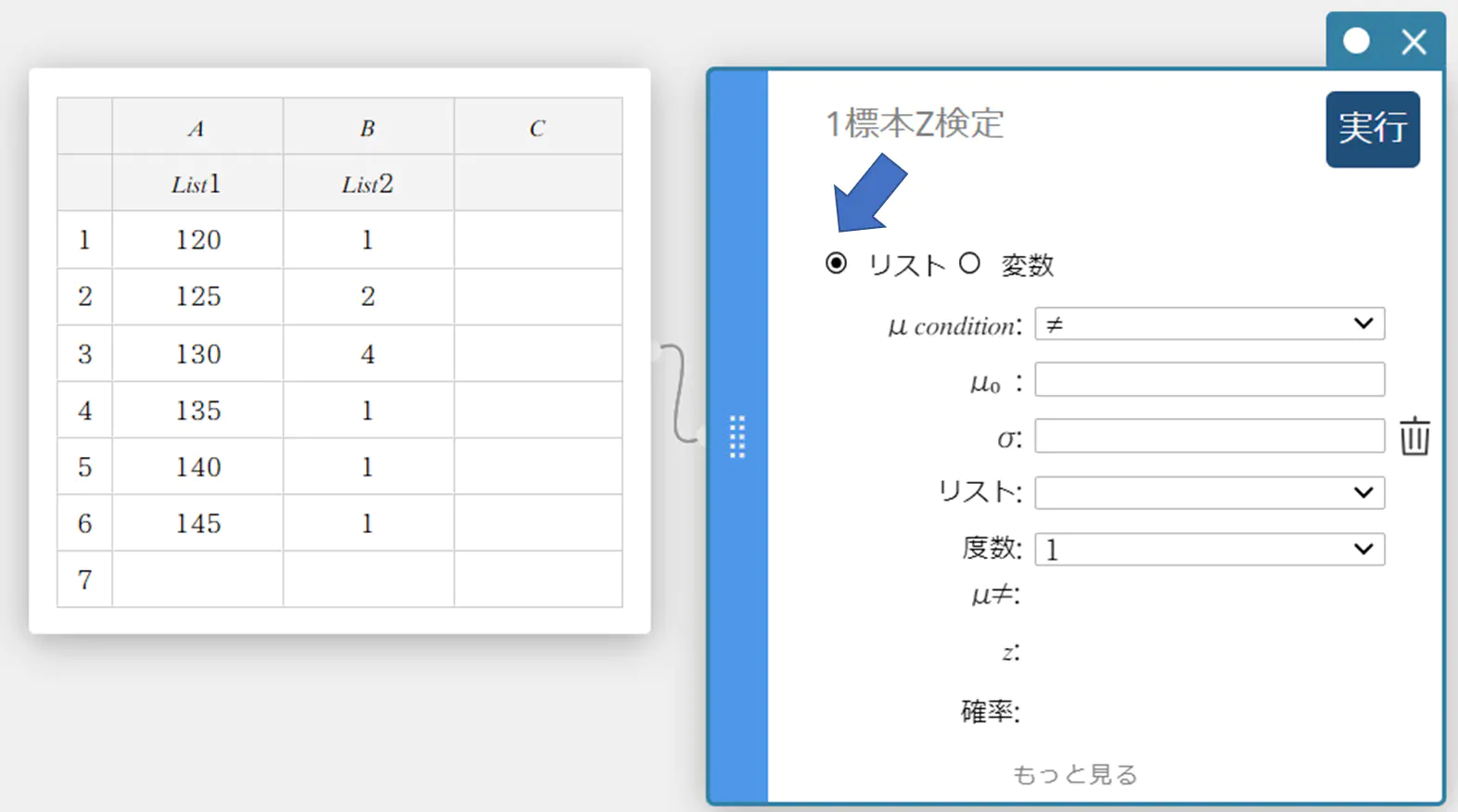
- 各項目に下記の値を入力する。
\(\mu\) condition: メニューから “\(\gt\)” を選択
\(\mu_0\) : \(120\)
\(\sigma\): \(19\)
リスト: メニューから “List1” を選択
度数: メニューから “List2” を選択
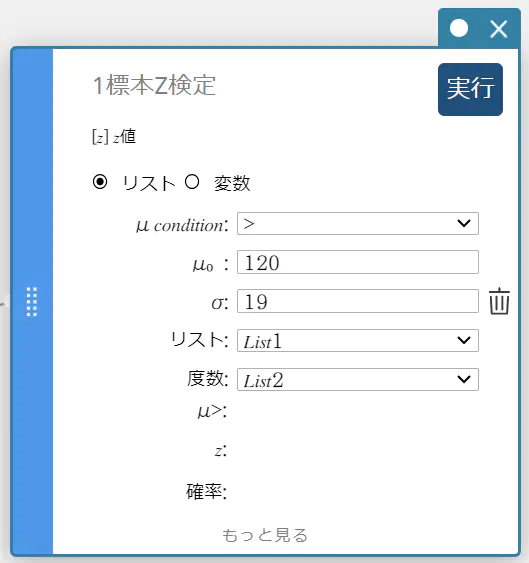
- 【実行】をクリックする。
計算結果が表示され、グラフスティッキーにグラフが描画されます。
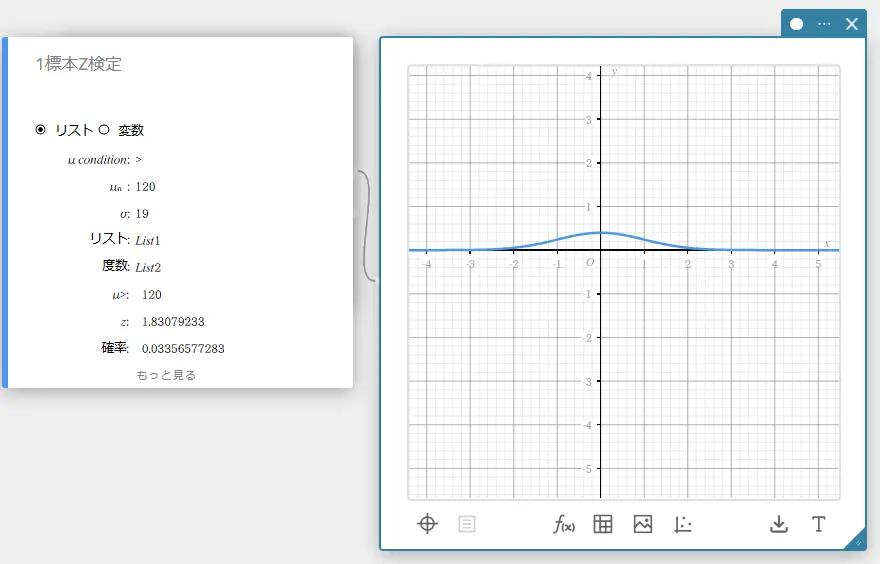
\(\mu \gt\) 母平均条件
\(\rm z\) \(\rm z\) 値
確率 \(\rm p\) 値
\(\overline{x}\) 標本平均値
\({\rm Sx}\) 標本標準偏差
\(n\) 標本データ数
統計計算と統計グラフ
統計計算
1変数統計計算
1変数統計計算の結果を表示します。
\(\bar{\rm x}\) … 標本平均値
\(\Sigma {\rm x}\) … データの総和
\(\Sigma {\rm x}^2\) … データの二乗和
\(\sigma {\rm x}\) … 母標準偏差
\({\rm sx}\) … 標本標準偏差
\({\rm n}\) … 標本データ数
\({\rm min(x)}\) … データの最小値
\({\rm Q}_1\) … データの第 1 四分位点(First Quartile)
\({\rm Med}\) … 中央値
\({\rm Q}_3\) … データの第 3 四分位点(Third Quartile)
\({\rm max(x)}\) … データの最大値
\({\rm Mode}\) … データの最頻値
\({\rm ModeN}\) … データの最頻値の個数
\({\rm ModeF}\) … データの最頻値の度数
\({\rm Mode}\) が複数個の解を持つときは、それらすべてが表示されます。
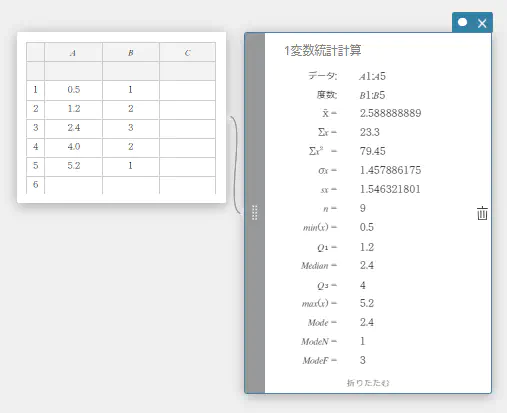
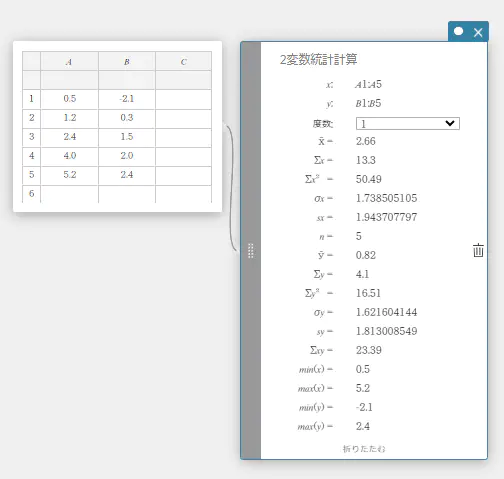
2変数統計計算
2変数統計計算の結果を表示します。
\(\bar{\rm x}\) … \(\rm X\) データの標本平均値
\(\Sigma {\rm x}\) … \(\rm X\) データの総和
\(\Sigma {\rm x}^2\) … \(\rm X\) データの二乗和
\(\sigma {\rm x}\) … \(\rm X\) データの母標準偏差
\({\rm sx}\) … \(\rm X\) データの標本標準偏差
\({\rm n}\) … 標本データ数
\(\bar{\rm y}\) … \(\rm Y\) データの標本平均値
\(\Sigma {\rm y}\) … \(\rm Y\) データの総和
\(\Sigma {\rm y}^2\) … \(\rm Y\) データの二乗和
\(\sigma {\rm y}\) … \(\rm Y\) データの母標準偏差
\({\rm sy}\) … \(\rm Y\) データの標本標準偏差
\(\Sigma {\rm xy}\) … \(\rm X\) データと \(\rm Y\) データの積の総和
\({\rm minX}\) … \(\rm X\) データの最小値
\({\rm maxX}\) … \(\rm X\) データの最大値
\({\rm minY}\)… \(\rm Y\) データの最小値
\({\rm maxY}\) … \(\rm Y\) データの最大値
回帰計算とグラフ
1次回帰
与えられたデータ点に最もよく一致する1次式を、最小二乗法を使って求め、直線の傾きとy切片の値を返します。その関係をグラフに表したものが1次回帰グラフです。
\(y = a \cdot x + b\)
\(a\) … 回帰式の一次係数(傾き)
\(b\) … 回帰式の定数項(y切片)
\(r\) … 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
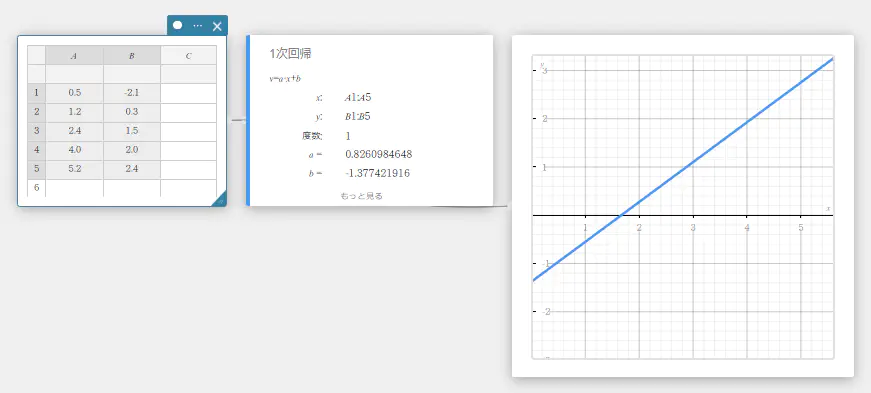
Med-Medグラフ
データに外れ値が含まれていることが考えられる場合、1次回帰グラフの代わりにMed-Medグラフ(中央値に基づくグラフ)を使用することができます。Med-Medグラフは1次回帰グラフに似ていますが、外れ値の影響を最小限に抑えます。
\(y = a \cdot x + b\)
\(a\) … 回帰式の1次係数(傾き)
\(b\) … 回帰式の定数項(y切片)
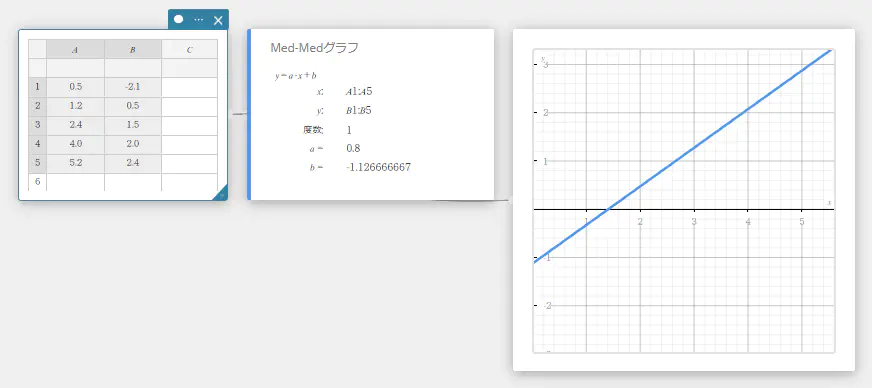
2次回帰
2次回帰グラフは最小二乗法を使って、できるだけ多くのデータ点の近くを通る2次曲線を描画します。このグラフは、2次回帰式として表すことができます。
\(y = a \cdot x^2 + b \cdot x + c\)
\(a\) … 回帰式の2次係数
\(b\) … 回帰式の1次係数
\(c\) … 回帰式の定数項(y切片)
\(r^2\) … 決定係数
MSe … 平均二乗誤差
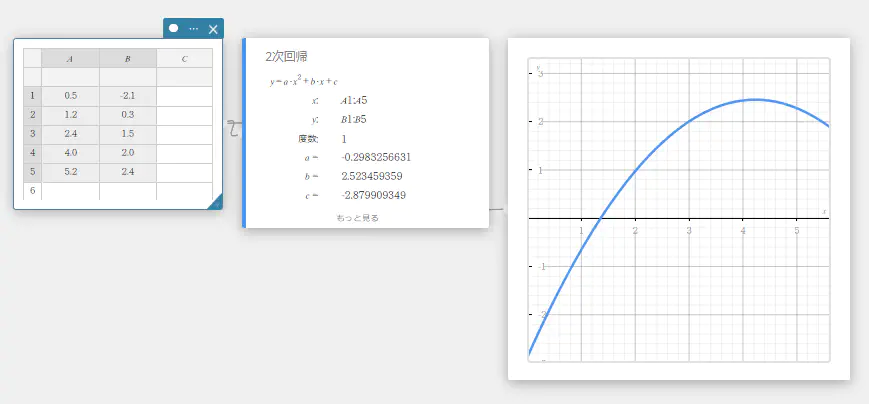
3次回帰
3次回帰グラフは最小二乗法を使って、できるだけ多くのデータ点の近くを通る3次曲線を描画します。このグラフは、3次回帰式として表すことができます。
\(y = a \cdot x^3 + b \cdot x^2 + c \cdot x + d\)
\(a\) … 回帰式の3次係数
\(b\) … 回帰式の2次係数
\(c\) … 回帰式の1次係数
\(d\) … 回帰式の定数項(y切片)
\(r^2\) … 決定係数
MSe … 平均二乗誤差
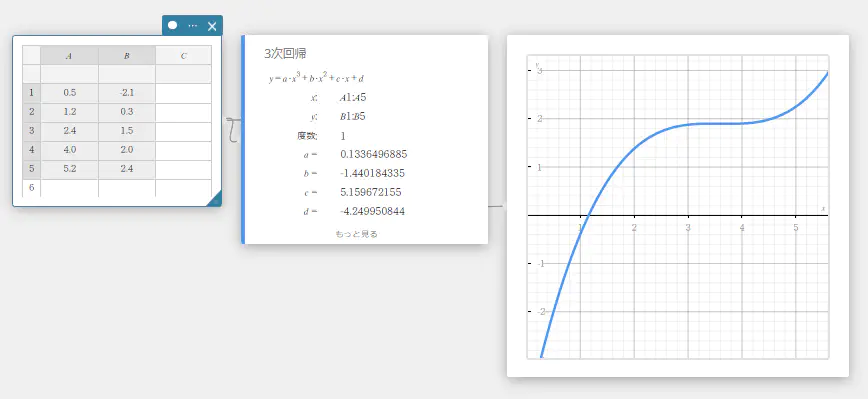
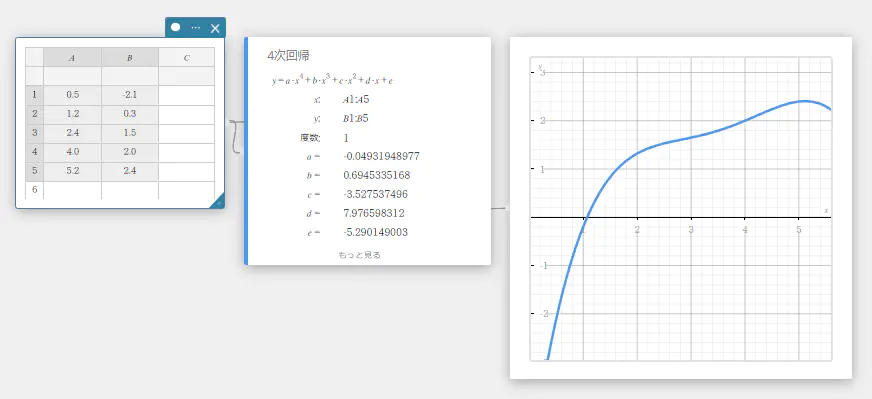
4次回帰
4次回帰グラフは最小二乗法を使って、できるだけ多くのデータ点の近くを通る4次曲線を描画します。このグラフは、4次回帰式として表すことができます。
\(y = a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e\)
\(a\) … 回帰式の4次係数
\(b\) … 回帰式の3次係数
\(c\) … 回帰式の2次係数
\(d\) … 回帰式の1次係数
\(e\) … 回帰式の定数項(y切片)
\(r^2\) … 決定係数
MSe … 平均二乗誤差
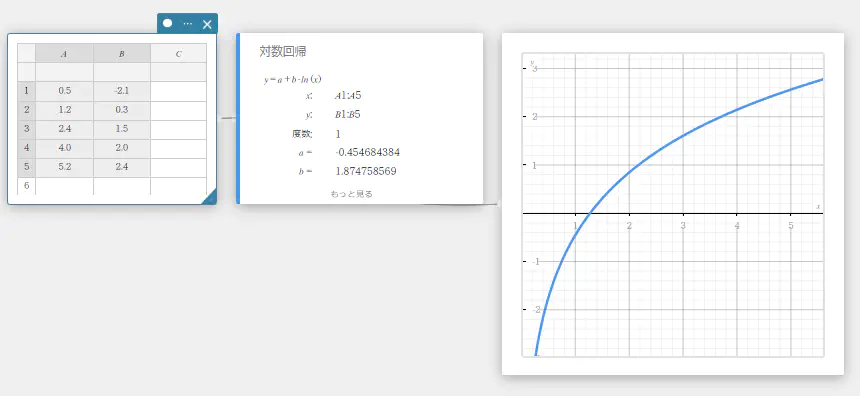
対数回帰
対数回帰は、\(y\) を \(x\) の対数関数として表します。対数回帰の一般式は \(y=a+b \cdot \ln(x)\) です。\(X=\ln(x)\) のとき、この式は1次回帰式 \(y=a+b \cdot X\) と対応します。
\(y = a + b \cdot \ln(x)\)
\(a\) … 回帰式の定数項
\(b\) … 回帰係数
\(r\) … 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
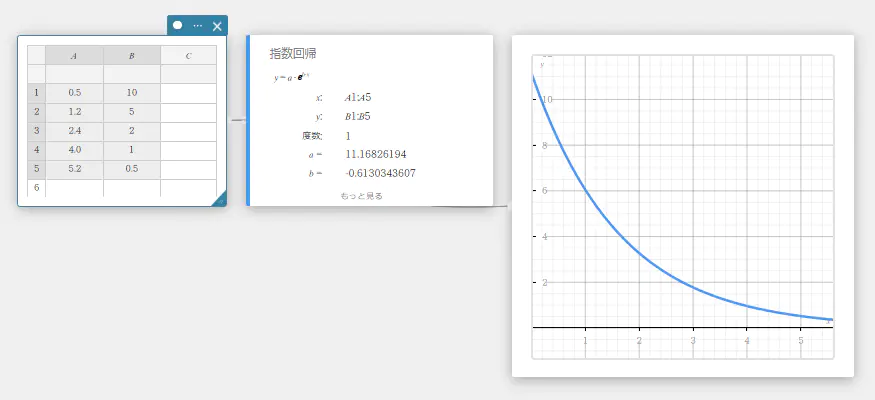
指数回帰
\(y\) が \(x\) の指数関数に比例する場合、指数回帰を使うことができます。指数回帰の一般式は \(y=a \cdot e^{b \cdot x}\) です。この式において両辺の自然対数をとると \(\ln(y)=\ln(a)+b \cdot x\) となります。次に \(Y=\ln(y)\)、\(A=\ln(a)\) とするとき、この式は1次回帰式 \(Y=A+b \cdot x\) と対応します。
\(y = a \cdot e^{b \cdot x}\)
\(a\) … 回帰係数
\(b\) … 回帰式の定数項
\(r\) … 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
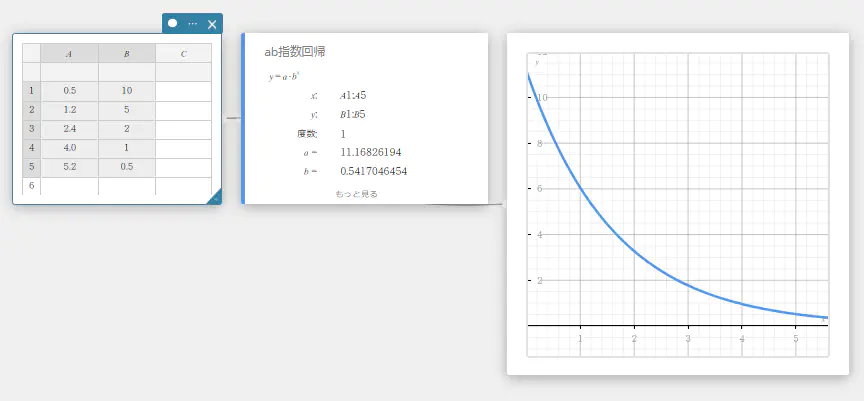
ab指数回帰
\(y\) が \(x\) の指数関数に比例する場合、指数回帰を使うことができます。 ab指数回帰では、指数回帰の一般式は \(y=a \cdot b^x\) です。この式において両辺の自然対数を取得すると、 \(\ln(y)=\ln(a)+(\ln(b)) \cdot x\) となります。次に \(Y=\ln(y)\)、\(A=\ln(a)\)、\(B=\ln(b)\) とするとき、この式は1次回帰式 \(Y=A+B \cdot x\) と対応します。
\(y = a \cdot b^x\)
\(a\) … 回帰式の定数項
\(b\) … 回帰係数
\(r\) … 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
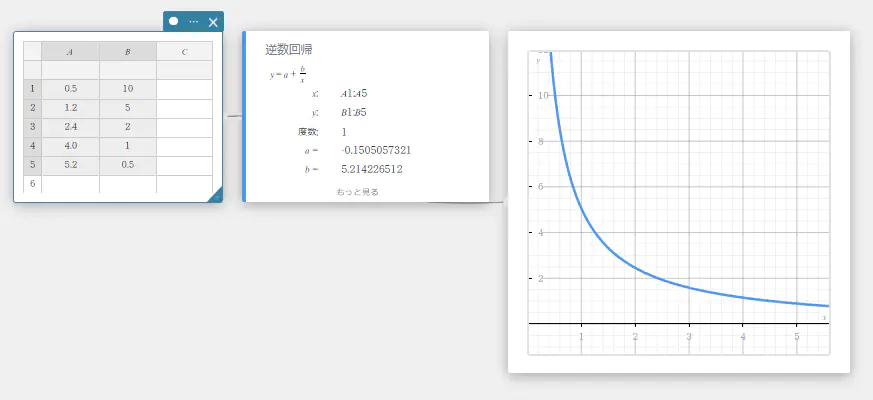
逆数回帰
逆数回帰は、\(y\) を \(x\) の逆関数として表します。逆数回帰の一般式は \(y=a+b/x\) です。\(X=1/x\) のとき、この式は1次回帰式 \(y=a+b・X\) と対応します。
\(y=a+b/x\)
\(a\) … 回帰式の定数項
\(b\) … 回帰係数
\(r\) …. 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
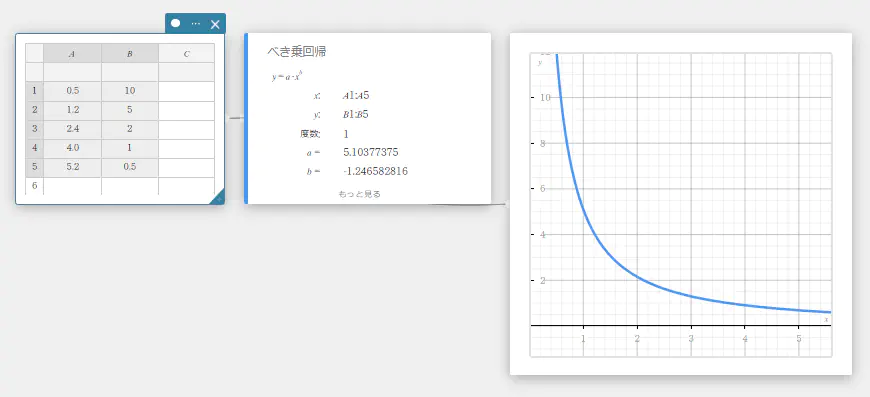
べき乗回帰
\(y\) が \(x\) のべき乗に比例する場合、べき乗回帰を使うことができます。べき乗回帰の一般式は \(y=a \cdot x^b\) です。この式において両辺の自然対数をとると、\(\ln(y)=\ln(a)+b \cdot \ln(x)\) となります。次に \(X=\ln(x)\)、\(Y=\ln(y)\)、\(A=\ln(a)\) とするとき、この式は1次回帰式 \(Y=A+b \cdot X\) と対応します。
\(y = a \cdot x^b\)
\(a\) … 回帰係数
\(b\) … 回帰べき
\(r\) … 相関係数
\(r^2\) … 決定係数
MSe … 平均二乗誤差
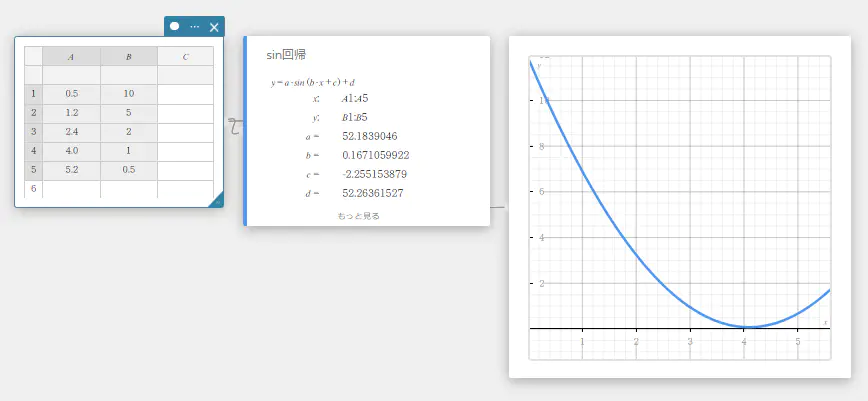
sin回帰
sin回帰は、一定の範囲内で周期的な変化を繰り返すようなデータに、よく適合します。
\(y = a \cdot \sin( b \cdot x + c ) + d\)
\(a\), \(b\), \(c\), \(d\) … 回帰係数
MSe … 平均二乗誤差
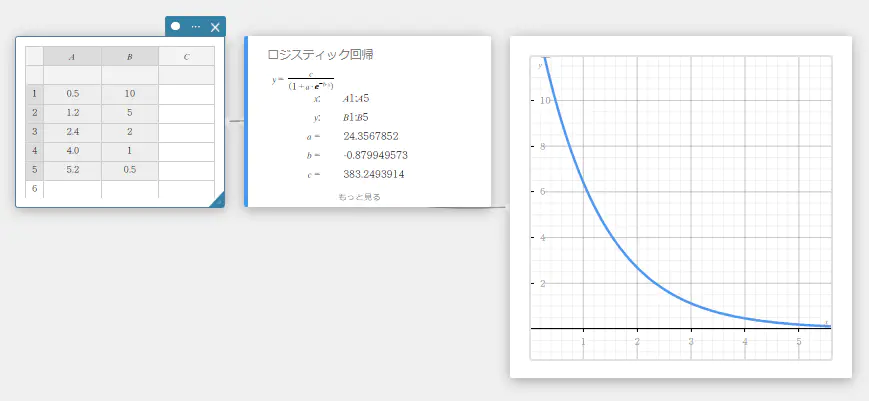
ロジスティック回帰
ロジスティック回帰は、飽和点に達するまで時間の経過とともに継続的に増加するようなデータに、よく適合します。
\(\displaystyle y=\frac{c}{1+a \cdot e^{-b \cdot x}}\)
\(a\), \(b\), \(c\) … 回帰係数
MSe … 平均二乗誤差
検定 
1標本Z検定
母標準偏差がわかっている場合に、仮定した母平均と単一の標本平均値を検定します。1標本Z検定では、正規分布を用います。
\(Z=\displaystyle \frac{\overline{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\)
\(\overline{x}\) : 標本平均値
\(\mu_{0}\) : 仮定母平均
\(\sigma\) : 母標準偏差
\(n\) : 標本データ数
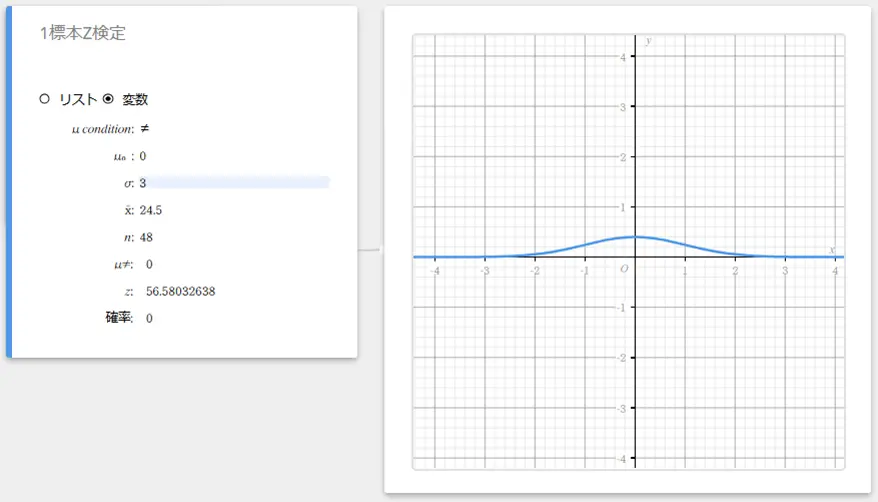
データとして変数を使う場合:
- 入力値の用語
\( \mu \) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
\( \mu_{0} \) : 仮定母平均
\( \sigma \) : 母標準偏差(\( \sigma > 0 \))
\(\overline{x}\) : 標本平均値
\(n\) : 標本データ数(正の整数) -
出力値の用語
\( \mu \neq \) : 母平均条件
\(z\) : \(z\) 値
確率 : \(p\) 値
データとしてリストを使う場合:
- 入力値の用語
\( \mu \) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
\( \mu_{0} \) : 仮定母平均
\( \sigma \) : 母標準偏差(\( \sigma > 0 \))
リスト : データリスト
度数 : 度数(\(1\) またはリスト名) -
出力値の用語
\( \mu \neq \) : 母平均条件
\(z\) : \(z\) 値
確率 : \(p\) 値
\( \overline{x} \) : 標本平均値
\( s_{x} \) : 標本標準偏差
\( n \) : 標本データ数
2標本Z検定
2つの母集団の標準偏差がわかっている場合に、2つの標本平均値の有意差を検定します。2標本Z検定では、正規分布を用います。
\( Z=\displaystyle \frac{ \overline{x}_{1} – \overline{x}_{2} }{ \sqrt{\displaystyle \frac{{\sigma_{1}}^2}{n_{1}} +\displaystyle \frac{{\sigma_{2}}^2}{n_{2}} } } \)
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( \sigma_{1} \) : 標本1データの母標準偏差
\( \sigma_{2} \) : 標本2データの母標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
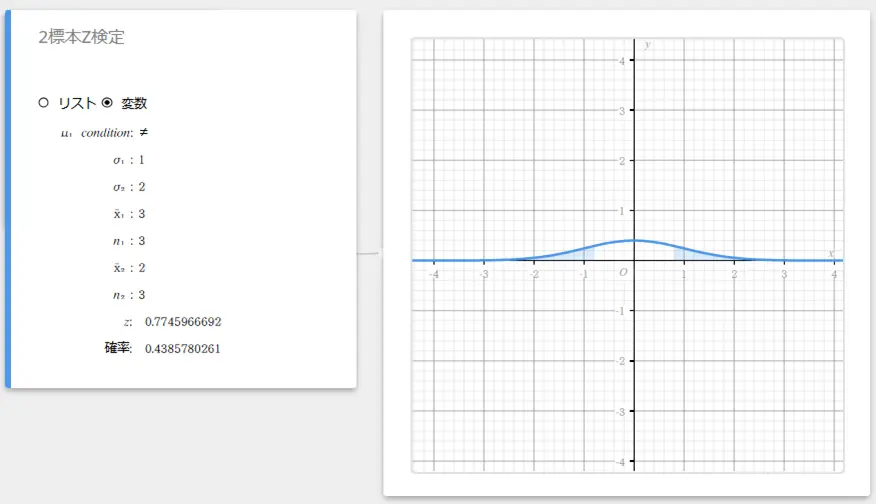
データとして変数を使う場合:
- 入力値の用語
\( \mu_{1} \) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は標本1が標本2より小さい片側検定、“\(\gt\)” は標本1が標本2より大きい片側検定)
\( \sigma_{1} \) : 標本1データの母標準偏差(\( \sigma_{1} > 0 \))
\( \sigma_{2} \) : 標本2データの母標準偏差(\( \sigma_{2} > 0 \))
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( n_{1} \) : 標本1のサイズ(正の整数)
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( n_{2} \) : 標本2のサイズ(正の整数) -
出力値の用語
\(z\) : \(z\) 値
確率 : \(p\) 値
データとしてリストを使う場合:
- 入力値の用語
\( \mu_{1} \) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は標本1が標本2より小さい片側検定、“\(\gt\)” は標本1が標本2より大きい片側検定)
\( \sigma_{1} \) : 標本1データの母標準偏差(\( \sigma_{1} > 0 \))
\( \sigma_{2} \) : 標本2データの母標準偏差(\( \sigma_{2} > 0 \))
リスト(1) : 標本1データが格納されているリスト
リスト(2) : 標本2データが格納されているリスト
度数(1) : 標本1データの度数(\(1\) またはリスト名)
度数(2) : 標本2データの度数(\(1\) またはリスト名) -
出力値の用語
\(z\) : \(z\) 値
確率 : \(p\) 値
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( s_{x_{1}} \) : 標本1データの標本標準偏差
\( s_{x_{2}} \) : 標本2データの標本標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
1比率Z検定
仮定した母比率に対する、単一の標本比率を検定します。1比率Z検定では、正規分布を用います。
\(Z =\displaystyle \frac{\displaystyle \frac{x}{n} – p_{0} }{ \sqrt{\displaystyle \frac{ p_{0}(1-p_{0}) }{n} }}\)
\(p_{0}\) : 仮定母比率
\(n\) : 標本データ数
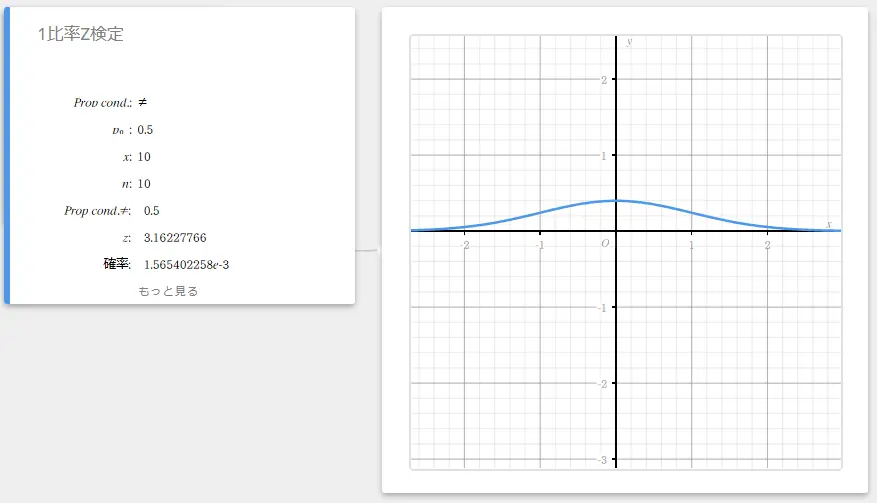
- 入力値の用語
Prop cond : 標本比率検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
\(p_{0}\) : 仮定母比率(\( 0 < p_{0} < 1 \))
\(x\) : 標本のデータ値(整数、 \( x \geq 0 \))
\(n\) : 標本データ数(正の整数) -
出力値の用語
Prop Cond \(\neq\) : 標本比率検定条件
\(z\) : \(z\) 値
確率 : \(p\) 値
\(\hat{p}\) : 推定標本比率
2比率Z検定
2つの標本比率の有意差を検定します。2比率Z検定では、正規分布を用います。
\( Z =\displaystyle \frac{\displaystyle \frac{x_{1}}{n_{1}} -\displaystyle \frac{x_{2}}{n_{2}} }{ \sqrt{ \hat{p} \left(1-\hat{p} \right) \left(\displaystyle \frac{1}{n_{1}} +\displaystyle \frac{1}{n_{2}} \right) } }\)
\(x_{1}\) : 標本1のデータ値
\(x_{2}\) : 標本2のデータ値
\(n_{1}\) : 標本1のサイズ
\(n_{2}\) : 標本2のサイズ
\(\hat{p}\) : 統合推定標本比率
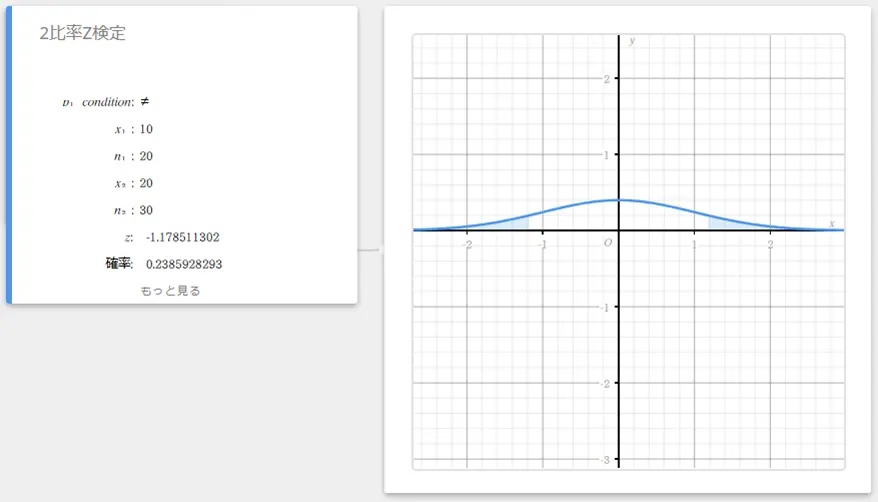
- 入力値の用語
\(p_{1}\) condition : 標本比率検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は標本1が標本2より小さい片側検定、“\(\gt\)” は標本1が標本2より大きい片側検定)
\(x_{1}\) : 標本1のデータ値(整数、 \(x_{1} \leq n_{1}\))
\(n_{1}\) : 標本1のサイズ(正の整数)
\(x_{2}\) : 標本2のデータ値(整数、 \(x_{2} \leq n_{2}\))
\(n_{2}\) : 標本2のサイズ(正の整数) -
出力値の用語
\(z\) : \(z\) 値
確率 : \(p\) 値
\(\hat{p}_{1}\) : 標本1の推定比率
\(\hat{p}_{2}\) : 標本2の推定比率
\(\hat{p}\) : 統合推定標本比率
1標本 \(t\) 検定
母標準偏差がわかっていない場合に、仮定した母平均に対する単一の標本平均値を検定します 。1標本 \(t\) 検定では、 \(t\) 分布を用います。
\(t =\displaystyle \frac{ \overline{x} – \mu_{0} }{\displaystyle \frac{ s_{x} }{ \sqrt{n} } }\)
\(\overline{x}\) : 標本平均値
\(\mu_{0}\) : 仮定母平均
\(s_{x}\) : 標本標準偏差
\(n\) : 標本データ数
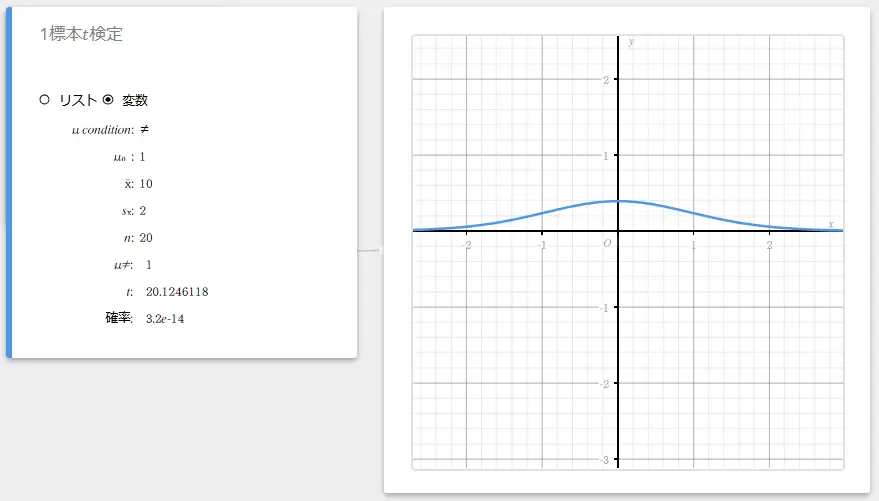
データとして変数を使う場合:
- 入力値の用語
\(\mu\) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
\(\mu_{0}\) : 仮定母平均
\(\overline{x}\) : 標本平均値
\(s_{x}\) : 標本標準偏差(\( s_{x} > 0 \))
\(n\) : 標本データ数(正の整数) -
出力値の用語
\(\mu \ne\) : 母平均検定条件
\(t\) : \(t\) 値
確率 : \(p\) 値
データとしてリストを使う場合:
- 入力値の用語
\(\mu\) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
\(\mu_{0}\) : 仮定母平均
リスト : データリスト
度数 : 度数(\(1\) またはリスト名) -
出力値の用語
\(\mu \ne\) : 母平均検定条件
\(t\) : \(t\) 値
確率 : \(p\) 値
\(\overline{x}\) : 標本平均値
\(s_{x}\) : 標本標準偏差
\(n\) : 標本データ数
2標本 \(t\) 検定
2つの母集団の母標準偏差がわかっていない場合に、2つの標本平均値の有意差を検定します 。2標本 \(t\) 検定では、 \(t\) 分布を用います。
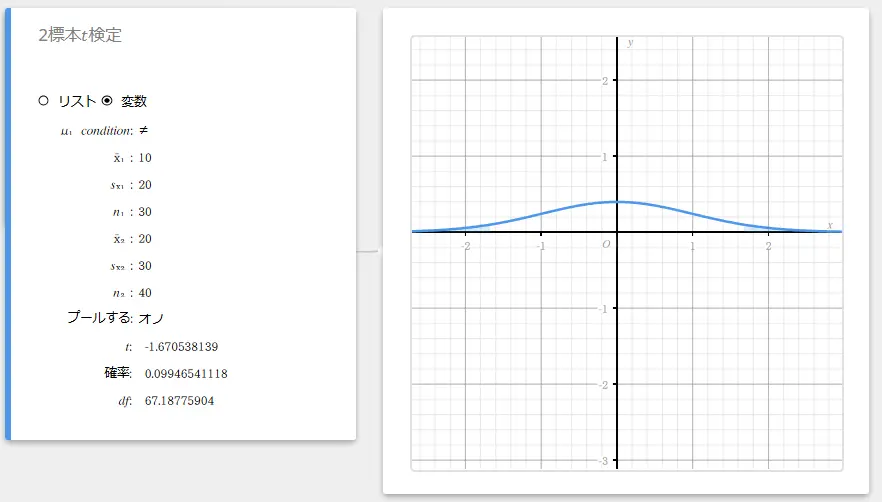
- 2つの母標準偏差が等しい(統合されている)場合
\(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{{s_{p}}^2 \left(\displaystyle \frac{1}{n_1} + \displaystyle \frac{1}{n_2} \right)}}\)
\(df=n_1+n_2-2\)
\(s_p=\sqrt{ \displaystyle \frac{(n_1-1){s_{x_1}}^2 + (n_2-1){s_{x_2}}^2}{n_1+n_2-2} }\) -
2つの母標準偏差が等しくない(統合されていない)場合
\(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{\displaystyle \frac{{s_{x_1}}^2}{n_1} + \displaystyle \frac{{s_{x_2}}^2}{n_2}}}\)
\(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{(1-C)^2}{n_2-1}}\)
\(C =\displaystyle \frac{\displaystyle \frac{{s_{x_1}}^2}{n_1}}{\displaystyle \frac{{s_{x_1}}^2}{n_1} +\displaystyle \frac{{s_{x_2}}^2}{n_2}}\)
\(x_1\): 標本1データの標本平均値
\(x_2\): 標本2データの標本平均値
\(s_{x_1}\) : 標本1データの標本標準偏差
\(s_{x_2}\) : 標本2データの標本標準偏差
\(s_p\) : 統合標本標準偏差
\(n_1\) : 標本1のサイズ
\(n_2\) : 標本2のサイズ
データとして変数を使う場合:
- 入力値の用語
\(\mu_1\) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は標本1が標本2より小さい片側検定、“\(\gt\)” は標本1が標本2より大きい片側検定)
\(\overline{x}_1\) : 標本1データの標本平均値
\(s_{x_1}\) : 標本1データの標本標準偏差(\(s_{x_1} > 0\))
\(n_1\) : 標本1のサイズ(正の整数)
\(\overline{x}_2\) : 標本2データの標本平均値
\(s_{x_2}\) : 標本2データの標本標準偏差(\(s_{x_2} > 0\))
\(n_2\) : 標本2のサイズ(正の整数) -
出力値の用語
\(t\) : \(t\) 値
確率 : \(p\) 値
\(df\) : 自由度
\(s_p\) : 統合標本標準偏差
データとしてリストを使う場合:
- 入力値の用語
\(\mu_1\) condition : 母平均検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は標本1が標本2より小さい片側検定、“\(\gt\)” は標本1が標本2より大きい片側検定)
リスト(1) : 標本1データが格納されているリスト
リスト(2) : 標本2データが格納されているリスト
度数(1) : 標本1データの度数( \(1\) またはリスト名)
度数(2) : 標本2データの度数( \(1\) またはリスト名)
プールする : オン(等分散)またはオフ(不等分散) -
出力値の用語
\(t\) : \(t\) 値
確率 : \(p\) 値
\(df\) : 自由度
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( s_{x_{1}} \) : 標本1データの標本標準偏差
\( s_{x_{2}} \) : 標本2データの標本標準偏差
\(s_p\) : 統合標本標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
1次回帰 \(t\) 検定
一組の変数(\(x\), \(y\))間の線形関係を検定します。回帰式 \(y = a + b \cdot x\) の係数 \(a\)、\(b\) を、最小二乗法で求めます。\(p\) 値は仮説が真、\(\beta = 0\) である場合の、回帰式の傾き(\(b\))の確率です。1次回帰 \(t\) 検定では、 \(t\) 分布を用います。
\(t=r\sqrt{\displaystyle \frac{n-2}{1-r^2}}\)
\( \displaystyle b=\left\{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) \right\} / \left\{\sum_{i=1}^n (x_i-\overline{x})^2 \right\}\)
\(a=\overline{y}-b\overline{x}\)
\(a\) : 回帰式の定数項(y切片)
\(b\) : 回帰式の1次係数(傾き)
\(n\) : 標本データ数(\(n \ge 3\))
\(r\) : 相関係数
\(r^2\) : 決定係数
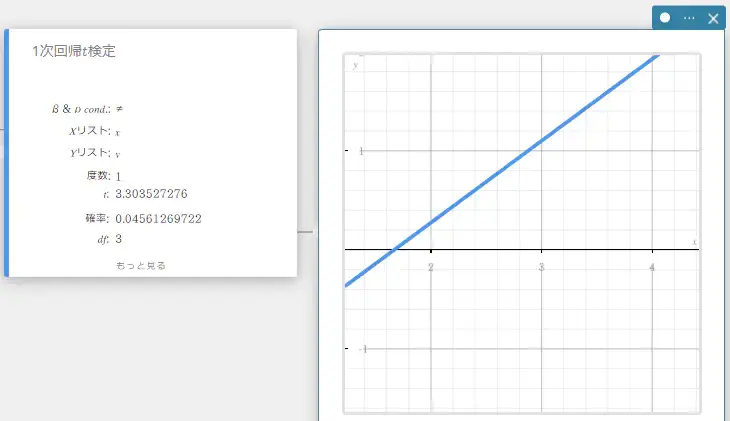
- 入力値の用語
\(\beta\ \&\ \rho\) cond : 検定条件(“\(\neq\)” は両側検定、“\(\lt\)” は下側の片側検定、“\(\gt\)” は上側の片側検定)
Xリスト : xデータのリスト
Yリスト : yデータのリスト
度数 : 度数(\(1\) またはリスト名) -
出力値の用語
\(t\) : \(t\) 値
確率 : \(p\) 値
\(df\) : 自由度
\(a\) : 回帰式の定数項(y切片)
\(b\) : 回帰式の1次係数(傾き)
se : 最小二乗法の回帰直線に関する推定の標準誤差
\(r\) : 相関係数
\(r^2\) : 決定係数
SEb: 最小二乗法の傾きの標準誤差
\(\chi^2\) 独立性検定
2つにカテゴリー分けされた行列形式の変数について、独立性を検定します。カイ2乗( \(\chi^2\) )独立性検定は、理論上の期待度数の行列と、観測値の行列を比較します。 \(\chi^2\) 独立性検定では、 \(\chi^2\) 分布を用います。
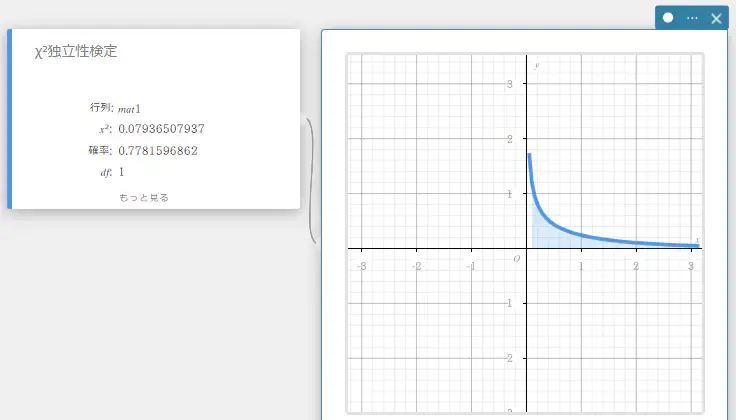
MEMO
行列の最小サイズは1行2列です。1列しかない行列を使うと、エラーとなります。
期待度数の計算結果は、システム変数の “期待度数” に格納されます。
\( \chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{l} \displaystyle \frac{(x_{ij}-F_{ij})^2}{F_{ij}} \)
\( F_{ij}=\frac{{\displaystyle\sum_{i=1}^k}x_{ij}\times{\displaystyle\sum_{j=1}^lx_{ij}}}{{\displaystyle\sum_{i=1}^k}{\displaystyle\sum_{j=1}^l}x_{ij}} \)
\( x_{ij}\) : 観測値行列の \(i\) 行 \(j\) 列の要素
\( F_{ij}\) : 期待度数行列の \(i\) 行 \(j\) 列の要素
- 入力値の用語
行列: 観測値を格納した行列の名前(行列が2行2列以上の場合、すべての要素は正の整数; 1行の場合、すべての要素は実数) -
出力値の用語
\(\chi^2\) : \(\chi^2\) 値
確率 : \(p\) 値
\(df\) : 自由度
観測値 : 観測値行列(入力値)
期待度数 : 期待度数行列(計算結果)
\(\chi^2\) 適合度検定
標本データの度数が、特定の分布に適合するかどうかを検定します。例えば、正規分布や2項分布との適合度を判定するために使用できます。
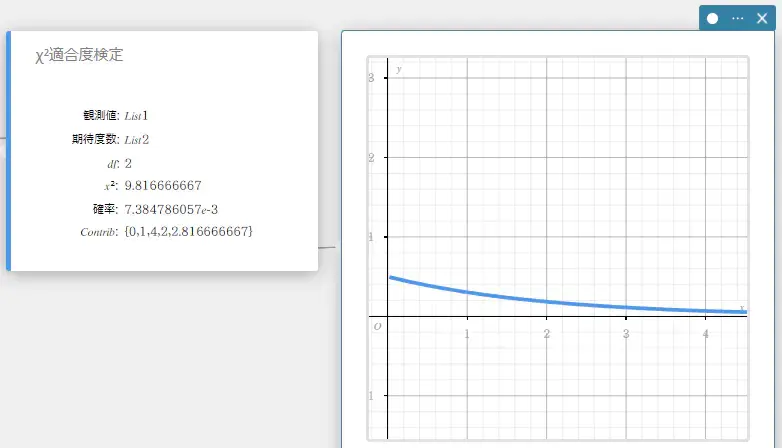
\(\chi^2=\sum_i^k \displaystyle \frac{ (O_i – E_i )^2 }{E_i}\)
\(Contrib = \left\{\displaystyle \frac{ (O_1 – E_1 )^2 }{E_1} \ \displaystyle \frac{ (O_2 – E_2 )^2 }{E_2} \cdots \displaystyle \frac{ (O_k – E_k )^2 }{E_k} \right\} \)
\(O_i\) : 観測値リストの \(i\) 番目の要素
\(E_i\) : 期待度数リストの \(i\) 番目の要素
- 入力値の用語
観測値 : 度数を保存したリストの名前(リストのすべての要素は正の整数)
期待度数 : 期待度数を保存するためのリストの名前
\(df\) : 自由度 -
出力値の用語
\(\chi^2\) : \(\chi^2\) 値
確率 : \(p\) 値
\(df\) : 自由度
Contrib : \(\Sigma\) 内の各項を保存するためのリストの名前
2標本F検定
無作為抽出した2つの独立したランダムな標本の、母分散の比率を検定します。2標本F検定では、F 分布を用います。
\( F=\displaystyle \frac{{S_{x_1}}^2}{{S_{x_2}}^2}\)
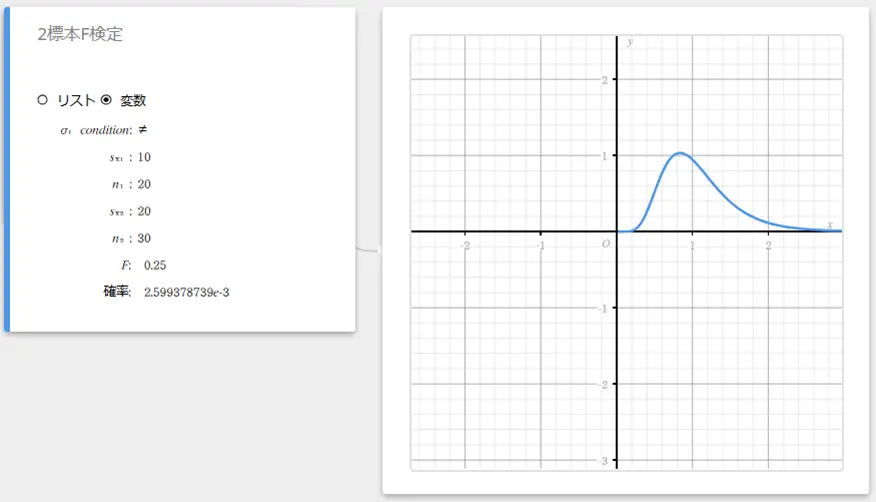
データとして変数を使う場合:
- 入力値の用語
\( \sigma_1\) condition: 母標準偏差検定条件(“ \( \neq\)” は両側検定、“ \( \lt\)” は標本1が標本2より小さい片側検定、“ \( \gt\)” は標本1が標本2より大きい片側検定)
\( s_{x_1}\) : 標本1データの標本標準偏差( \( s_{x_1} > 0\))
\( n_1\) : 標本1のサイズ(正の整数)
\( s_{x_2}\) : 標本2データの標本標準偏差( \( s_{x_2} > 0\))
\( n_2\) : 標本2のサイズ(正の整数) -
出力値の用語
\( F\) :\( F\) 値
確率 :\( p\) 値
データとしてリストを使う場合:
- 入力値の用語
\( \sigma_1\) condition: 母標準偏差検定条件(“ \( \neq\)” は両側検定、“ \( \lt\)” は標本1が標本2より小さい片側検定、“ \( \gt\)” は標本1が標本2より大きい片側検定)
リスト(1) : 標本1データが格納されているリスト
リスト(2) : 標本2データが格納されているリスト
度数(1) : 標本1データの度数( \( 1\) またはリスト名)
度数(2) : 標本2データの度数( \( 1\) またはリスト名) -
出力値の用語
\( F\) :\( F\) 値
確率 :\( p\) 値
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( s_{x_{1}} \) : 標本1データの標本標準偏差
\( s_{x_{2}} \) : 標本2データの標本標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
一元配置分散分析
複数の母集団の母平均が等しいという仮説を検定します。単一の独立変数または因子に基づいて、1つ以上のグループの平均を比較します。
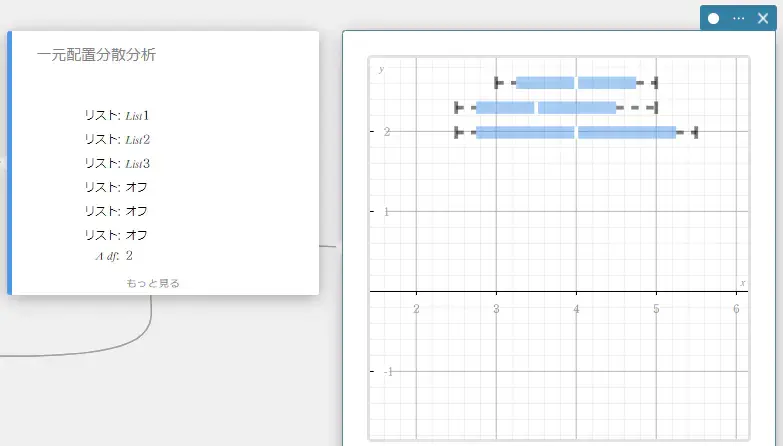
- 入力値の用語
FactorList(A) : 因子 A の水準が入っているリスト
DependentList : 標本データが入っているリスト -
出力値の用語
A \(df\) : 因子 A の自由度
A \(MS\) : 因子 A の平均平方
A \(SS\) : 因子 A の二乗和
A \(F\) : 因子 A の \(F\) 値
A \(p\) : 因子 A の \(p\) 値
Err\(df\) : 誤差の自由度
Err\(MS\) : 誤差の平均平方
Err\(SS\) : 誤差の二乗和
二元配置分散分析
複数の母集団の母平均が等しいという仮説を検定します。従属変数に基づいて、各変数個別の影響や相互作用を調べます。
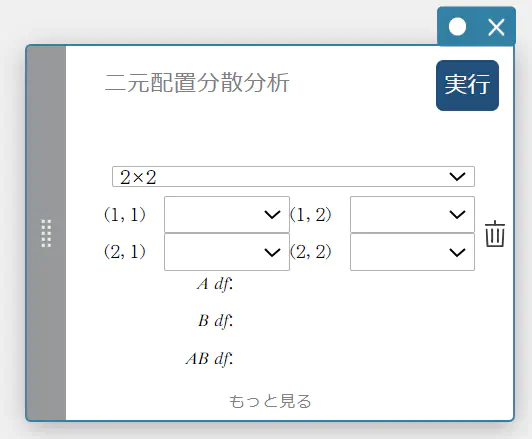
- 入力値の用語
2×2: データテーブルのタイプ
FactorList(A) : 因子 A の水準が入っているリスト
FactorList(B) : 因子 B の水準が入っているリスト
DependentList : 標本データが入っているリスト -
出力値の用語
A \(df\) : 因子 A の自由度
A \(MS\) : 因子 A の平均平方
A \(SS\) : 因子 A の二乗和
A \(F\) : 因子 A の \(F\) 値
A \(p\) : 因子 A の \(p\) 値
B \(df\) : 因子 B の自由度
B \(MS\) : 因子 B の平均平方
B \(SS\) : 因子 B の二乗和
B \(F\) : 因子 B の \(F\) 値
B \(p\) : 因子 B の \(p\) 値
AB \(df\) : 因子 A \(\times\) 因子 B の自由度
AB \(MS\) : 因子 A \(\times\) 因子 B の平均平方
AB \(SS\) : 因子 A \(\times\) 因子 B の二乗和
AB \(F\) : 因子 A \(\times\) 因子 B の \(F\) 値
AB \(p\) : 因子 A \(\times\) 因子 B の \(p\) 値
Err\(df\) : 誤差の自由度
Err\(MS\) : 誤差の平均平方
Err\(SS\) : 誤差の二乗和
信頼区間 
1標本Z信頼区間
標本平均値、およびわかっている母標準偏差に基づいて、母平均の信頼区間を求めます。
\(Lower = \overline{x}-Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(Upper = \overline{x}+Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(\alpha\) は有意水準、\(100(1 – \alpha)\%\) は信頼水準です。例えば信頼水準が \(95\%\) の場合、\(0.95\) を入力すると \(\alpha = 1 – 0.95 = 0.05\) となります。
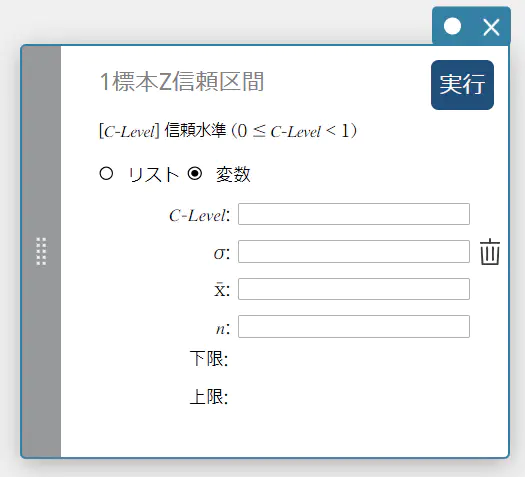
データとして変数を使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \sigma \) : 母標準偏差(\( \sigma > 0 \))
\( \overline{x} \) : 標本平均値
\( n \) : 標本データ数(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
データとしてリストを使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \sigma \) : 母標準偏差(\( \sigma > 0 \))
リスト : 標本データが入っているリスト
度数 : 標本の度数(\(1\) またはリスト名) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\( \overline{x} \) : 標本平均値
\( s_{x} \) : 標本標準偏差
\( n \) : 標本データ数
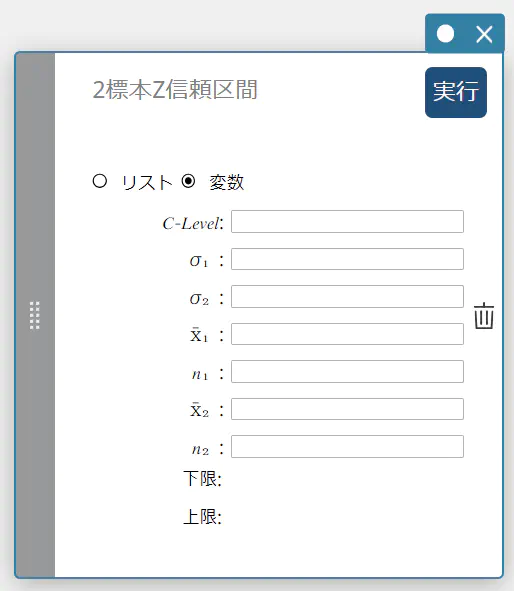
2標本Z信頼区間
母集団2つの母標準偏差がわかっている場合に、2つの標本平均値の差に基づいて、母平均の差の信頼区間を求めます。
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
データとして変数を使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \sigma_{1} \) : 標本1データの母標準偏差(\( \sigma_{1} > 0 \))
\( \sigma_{2} \) : 標本2データの母標準偏差(\( \sigma_{2} > 0 \))
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( n_{1} \) : 標本1のサイズ(正の整数)
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( n_{2} \) : 標本2のサイズ(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
データとしてリストを使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \sigma_{1} \) : 標本1データの母標準偏差(\( \sigma_{1} > 0 \))
\( \sigma_{2} \) : 標本2データの母標準偏差(\( \sigma_{2} > 0 \))
リスト(1) : 標本1データが格納されているリスト
リスト(2) : 標本2データが格納されているリスト
度数(1) : 標本1データの度数(\(1\) またはリスト名)
度数(2) : 標本2データの度数(\(1\) またはリスト名) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( s_{x_{1}} \) : 標本1データの標本標準偏差
\( s_{x_{2}} \) : 標本2データの標本標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
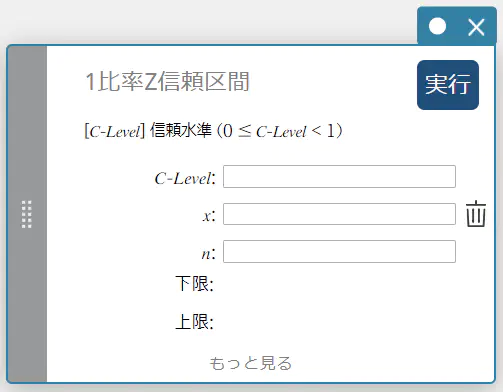
1比率Z信頼区間
単一の標本比率に基づいて、母集団比率の信頼区間を求めます。
\(Lower =\displaystyle \frac{x}{n}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
\(Upper =\displaystyle \frac{x}{n}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( x \) : データ(\(0\) または正の整数)
\( n \) : 標本データ数(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\(\hat{p}\) : 推定標本比率
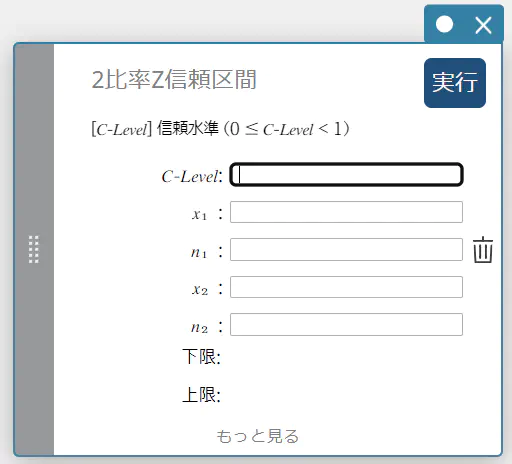
2比率Z信頼区間
2比率Z信頼区間の差に基づいて、母集団比率の差の信頼区間を求めます。
\( Lower =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1- \displaystyle\frac{x_1}{n_1} \right) }{n_1} + \displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1- \displaystyle \frac{x_2}{n_2} \right) }{n_2} } \)
\( Upper =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1-\displaystyle \frac{x_1}{n_1} \right) }{n_1} +\displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1-\displaystyle\frac{x_2}{n_2} \right) }{n_2} } \)
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\(x_{1}\) : 標本1のデータ値(整数、\(x_{1} \leq n_{1}\))
\(n_{1}\) : 標本1のサイズ(正の整数)
\(x_{2}\) : 標本2のデータ値(整数、\(x_{2} \leq n_{2}\))
\(n_{2}\) : 標本2のサイズ(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\(\hat{p}_{1}\) : 標本1の推定比率
\(\hat{p}_{2}\) : 標本2の推定比率
1標本 \(t\) 信頼区間
母標準偏差がわかっていない場合に、標本平均値と標本標準偏差に基づいて、母平均の信頼区間を求めます。
\(Lower = \overline{x}-t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
\(Upper = \overline{x}+t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
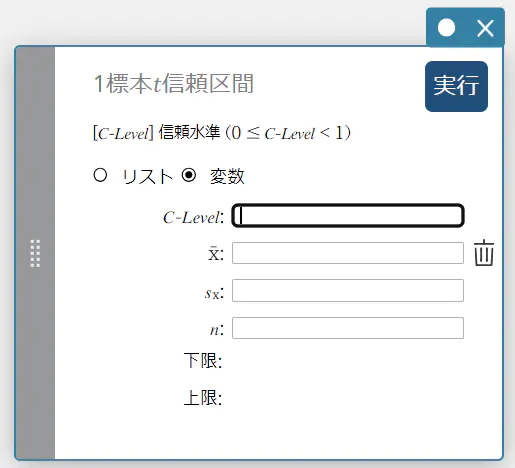
データとして変数を使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \overline{x} \) : 標本平均値
\(s_{x}\) : 標本標準偏差(\( s_{x} \ge 0 \))
\(n\) : 標本データ数(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
データとしてリストを使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
リスト : 標本データが入っているリスト
度数 : 標本の度数(\(1\) またはリスト名) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\( \overline{x} \) : 標本平均値
\( s_{x} \) : 標本標準偏差
\( n \) : 標本データ数
2標本 \(t\) 信頼区間
2つの母集団の母標準偏差がわかっていない場合に、標本平均値と標本標準偏差の差に基づいて、母平均の差の信頼区間を求めます。
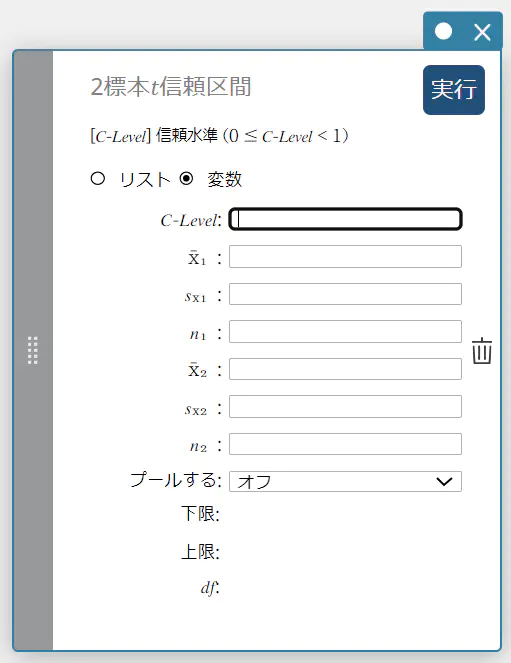
- 2つの母標準偏差が等しい(プールされている)場合
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
- 2つの母標準偏差が等しくない(プールされていない)場合
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
\(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{ \left( 1-C \right) ^2}{n_2-1}}\)
\(C=\displaystyle \frac{\displaystyle \frac{{S_{x_1}}^2}{n_1}}{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1} + \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
データとして変数を使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
\( \overline{x}_{1} \) : 標本1データの標本平均値
\(s_{x_1}\) : 標本1データの標本標準偏差(\(s_{x_1} \ge 0\))
\( n_{1} \) : 標本1のサイズ(正の整数)
\( \overline{x}_{2} \) : 標本2データの標本平均値
\(s_{x_2}\) : 標本2データの標本標準偏差(\(s_{x_2} \ge 0\))
\( n_{2} \) : 標本2のサイズ(正の整数) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\(df\) : 自由度
\(s_p\) : プール標本標準偏差
データとしてリストを使う場合:
- 入力値の用語
C-Level : 信頼水準(\(0 \le\) C-Level \(\lt 1\))
リスト(1) : 標本1データが格納されているリスト
リスト(2) : 標本2データが格納されているリスト
度数(1) : 標本1データの度数(\(1\) またはリスト名)
度数(2) : 標本2データの度数(\(1\) またはリスト名)
プールする : オン(等分散) またはオフ(不等分散) -
出力値の用語
下限 : 区間の下端
上限 : 区間の上端
\(df\) : 自由度
\( \overline{x}_{1} \) : 標本1データの標本平均値
\( \overline{x}_{2} \) : 標本2データの標本平均値
\( s_{x_{1}} \) : 標本1データの標本標準偏差
\( s_{x_{2}} \) : 標本2データの標本標準偏差
\(s_p\) : プール標本標準偏差
\( n_{1} \) : 標本1のサイズ
\( n_{2} \) : 標本2のサイズ
分布
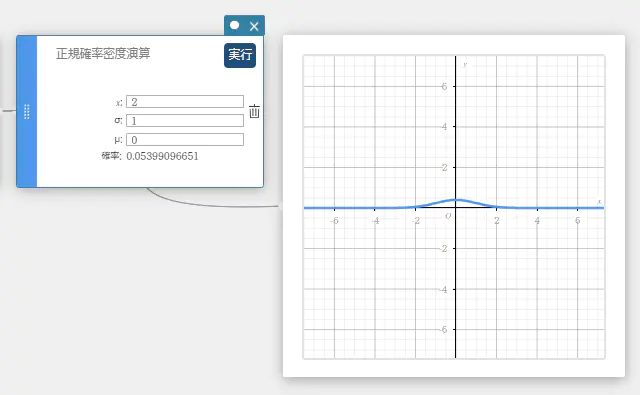
正規確率密度演算
指定された値に対する正規確率密度を求めます。
\(\sigma=1\)、\(\mu=0\) を指定すると、標準正規分布になります。
\(\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \qquad (\sigma>0)\)
- 入力値の用語
\( x \) : データ値
\( \sigma \) : 母標準偏差 (\( \sigma > 0 \))
\( \mu \) : 母平均
-
出力値の用語
確率 : 正規確率密度
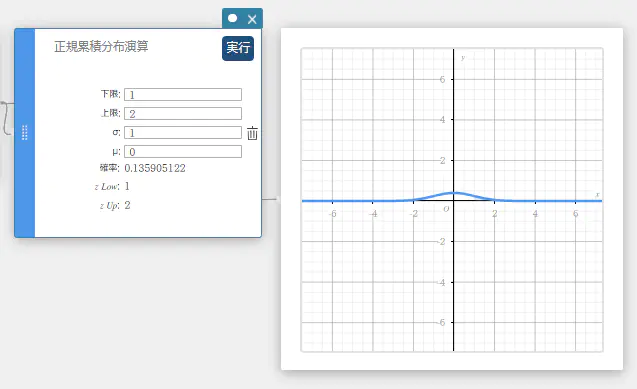
正規累積分布演算 
指定された下端 \((a)\) と上端 \((b)\) の間における、正規分布の累積確率を求めます。
\(\displaystyle p=\frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{ \scriptscriptstyle -\frac{(x-\mu)^2}{2\sigma^2} }dx\)
- 入力値の用語
下限 : 下端
上限 : 上端
\( \sigma \) : 母標準偏差 (\( \sigma > 0 \))
\(\mu\) : 母平均 -
出力値の用語
確率 : 正規分布確率 \(p\)
\(z {\rm Low}\) : 標準化下端 \(z\) 値
\(z {\rm Up}\) : 標準化上端 \(z\) 値
スチューデントの \(t\) 確率密度演算 
指定された値に対するスチューデントの \(t\) 確率密度を求めます。
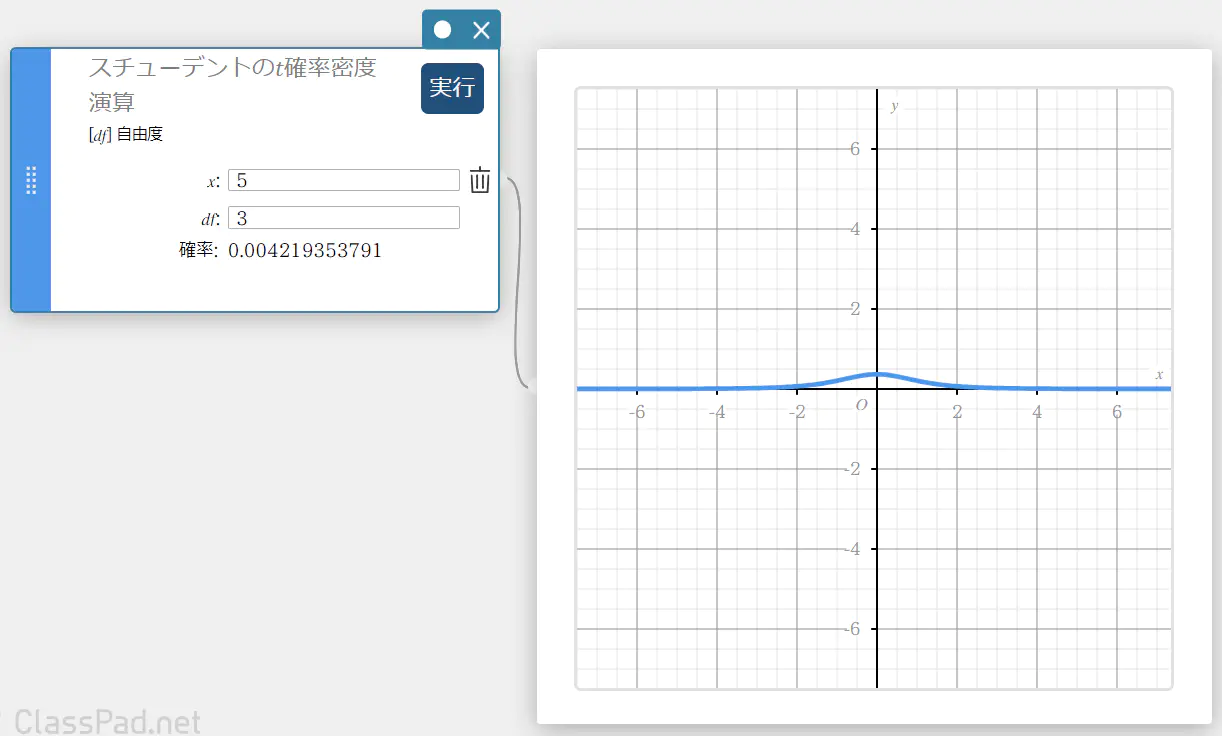
\(f(x)=\frac{\Gamma\left({\displaystyle\frac{df+1}2}\right)}{\Gamma\left({\displaystyle\frac{df}2}\right)}\times\frac{\left(1+{\displaystyle\frac{x^2}{df}}\right)^{-{\displaystyle\frac{df+1}2}}}{\sqrt{\pi\cdot df}}\)
- 入力値の用語
\( x \) : データ値
\(df\) : 自由度(\(df \gt 0\)) -
出力値の用語
確率 : スチューデントの \(t\) 確率密度
スチューデントの \(t\) 累積分布演算 
指定された下端 \((a)\) と上端 \((b)\) の間における、スチューデントの \(t\) 分布の累積確率を求めます。
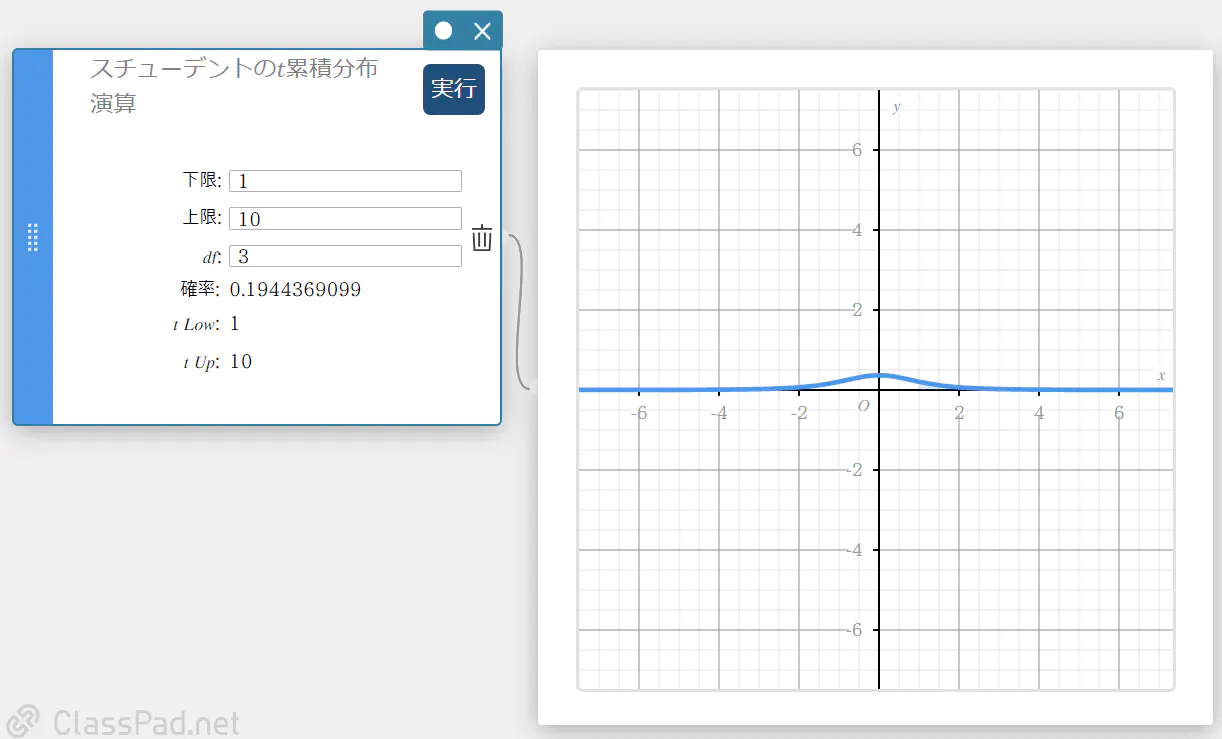
\( p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{df+1}{2} \right) }{\Gamma \left(\displaystyle \frac{df}{2} \right) \sqrt{\pi \cdot df}}\int_a^b \left(\displaystyle 1+\frac{x^2}{df} \right) ^{-\displaystyle\frac{df+1}{2}}dx \)
- 入力値の用語
下限 : 下端
上限 : 上端
\(df\) : 自由度(\(df \gt 0\)) -
出力値の用語
確率 : スチューデントの \(t\) 分布
\(t {\rm Low}\) : 下端の入力値
\(t {\rm Up}\) : 上端の入力値
\(\chi^2\) 確率密度演算 
指定された値に対する \(\chi^2\) 確率密度を求めます。
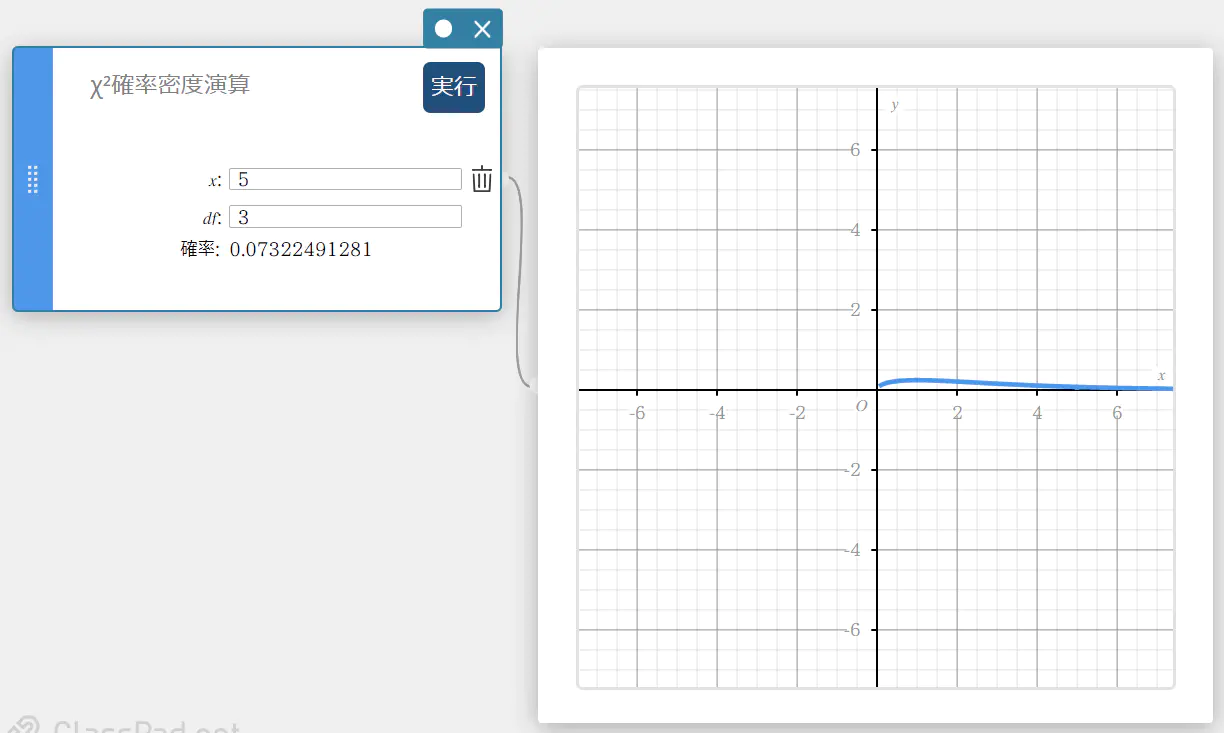
\(f \left( x \right) =\displaystyle\frac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}\)
- 入力値の用語
\( x \) : データ値
\(df\) : 自由度(正の整数) -
出力値の用語
確率 : \(\chi^2\) 確率密度
\(\chi^2\) 累積分布演算 
指定された下端 \((a)\) と上端 \((b)\) の間における、 \(\chi^2\) 分布の累積確率を求めます。
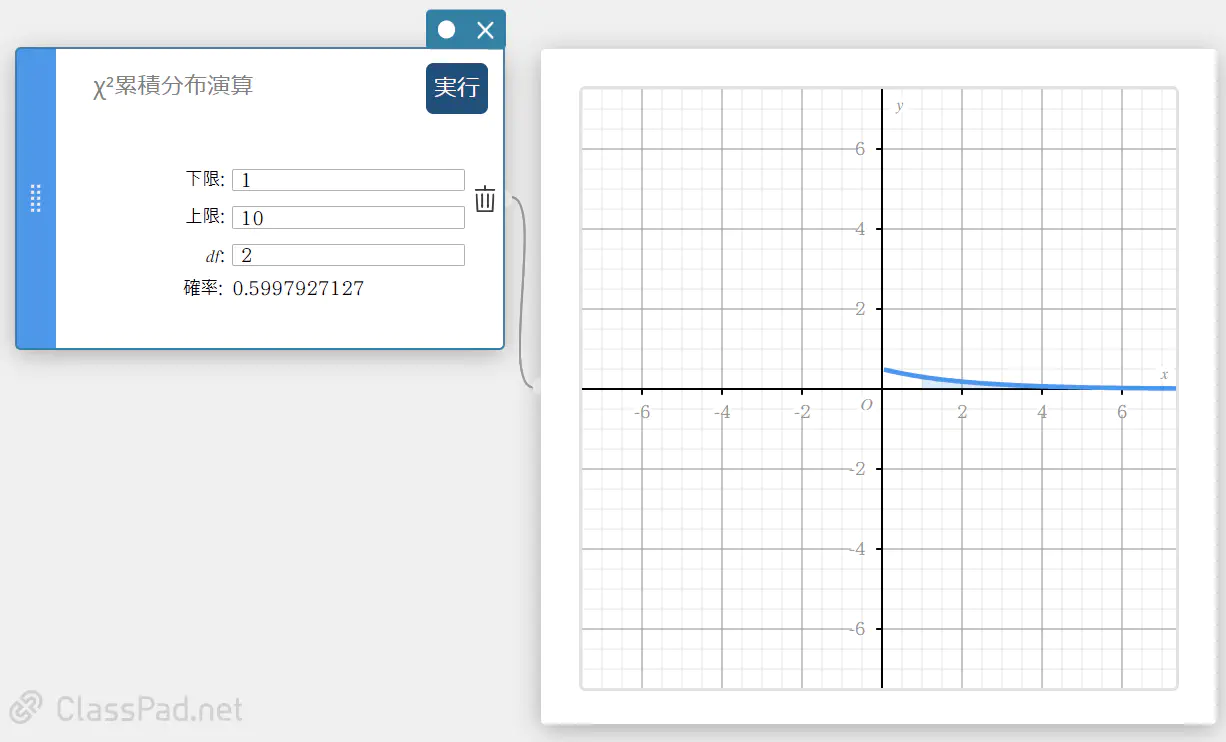
\(p=\cfrac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}\int_a^b x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}dx\)
- 入力値の用語
下限 : 下端
上限 : 上端
\(df\) : 自由度(正の整数) -
出力値の用語
確率 : \(\chi^2\) 分布確率
F 確率密度演算 
指定された値に対する F 確率密度を求めます。
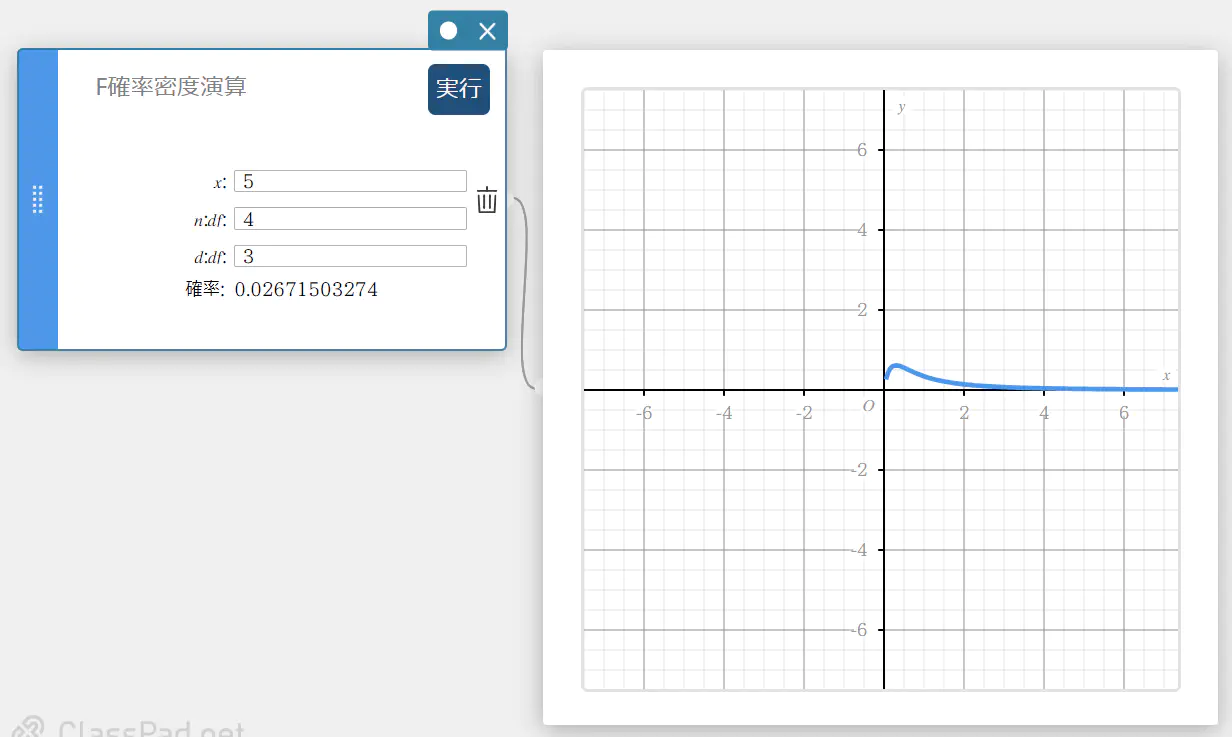
\(f(x)=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}\)
- 入力値の用語
\( x \) : データ値
\( n:df \) : 分子の自由度(正の整数)
\( d:df \) : 分母の自由度(正の整数) -
出力値の用語
確率 : F 確率密度
F 累積分布演算 
指定された下端 \((a)\) と上端 \((b)\) の間における、F 分布の累積確率を求めます。
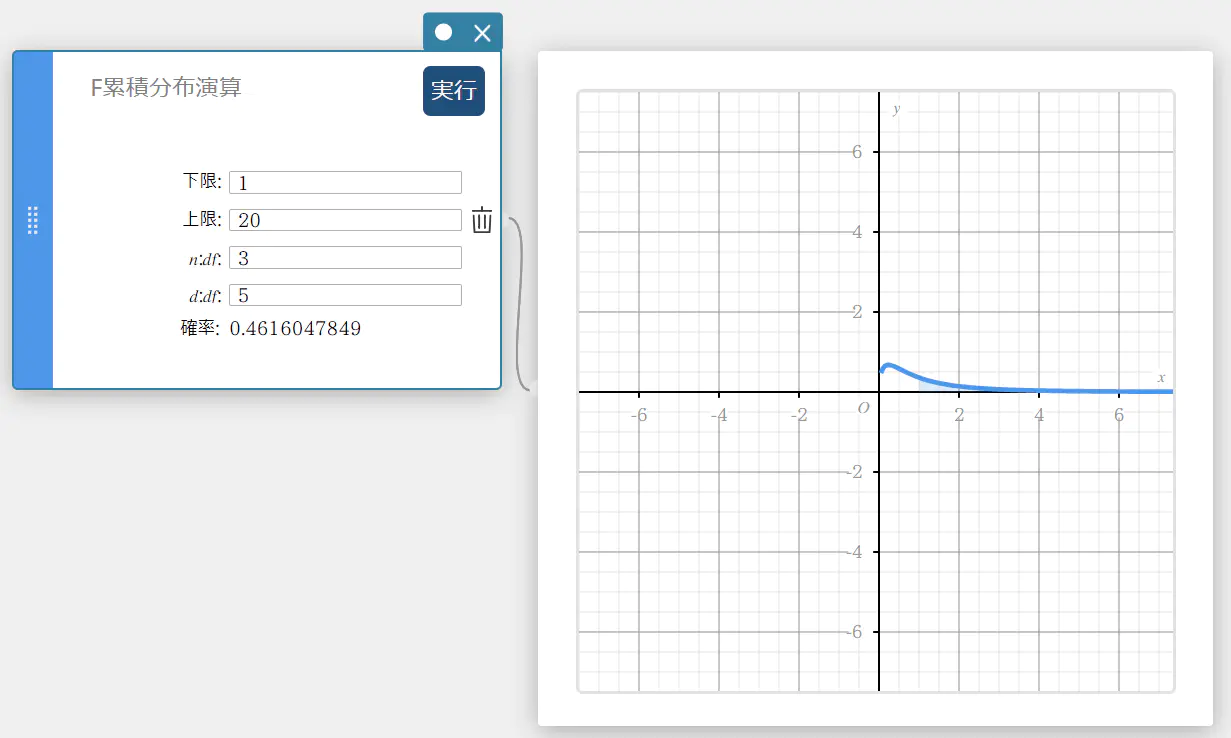
\(p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}\int_a^b x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}dx\)
- 入力値の用語
下限 : 下端
上限 : 上端
\( n:df \) : 分子の自由度(正の整数)
\( d:df \) : 分母の自由度(正の整数) -
出力値の用語
確率 : F 分布確率
2 項確率演算 
指定された試行において成功する 2 項分布の確率を求めます。
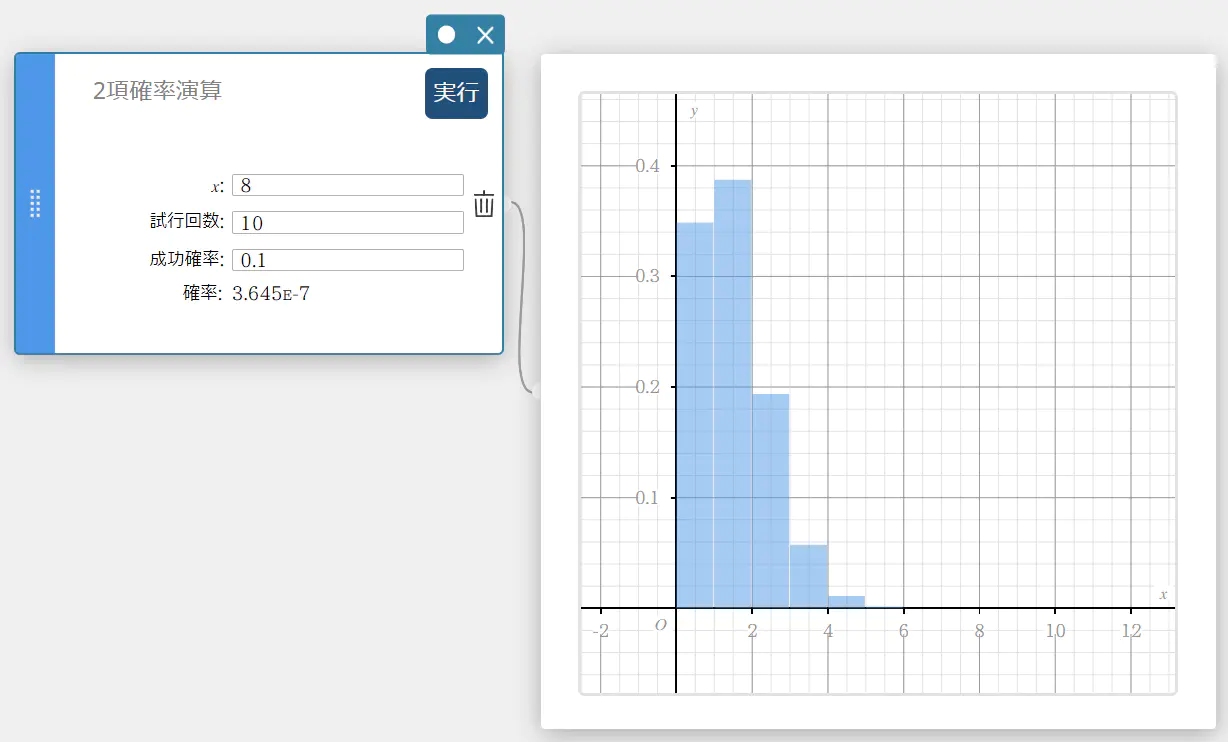
\(f(x)={}_nC_xp^x(1-p)^{n-x} \quad (x=0,1, \cdots,n)\)
\(p\) : 成功確率(\(0 \le p \le 1\))
\(n\) : 試行回数
- 入力値の用語
\( x \) : 指定試行値(\(0\) から \(n\) の整数)
試行回数 : 試行回数 \(n\)(整数、 \(n \ge 0\))
成功確率 : 成功確率 \(p\)(\(0 \le p \le 1\)) -
出力値の用語
確率 : 2 項確率
2 項累積分布演算 
指定された範囲において成功する、 2 項分布の累積確率を求めます。
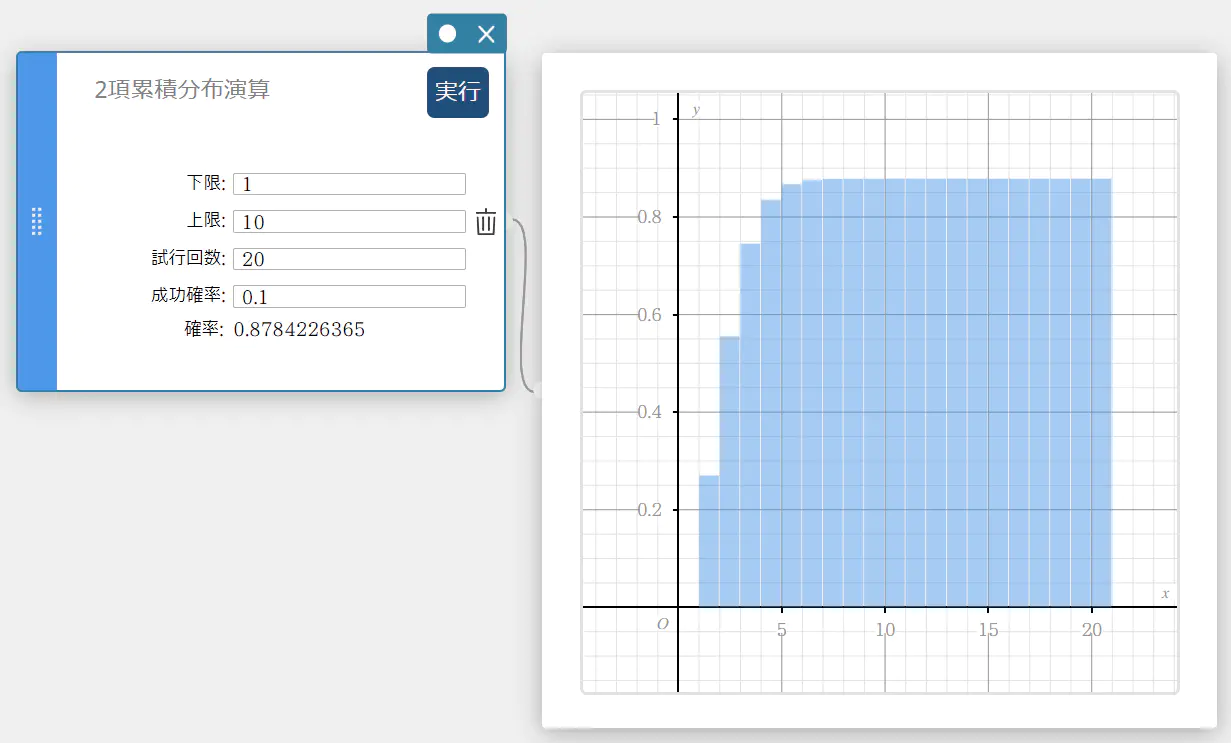
- 入力値の用語
下限 : 下端
上限 : 上端
試行回数 : 試行回数 \(n\)(整数、 \(n \ge 1\))
成功確率 : 成功確率 \(p\)(\(0 \le p \le 1\)) -
出力値の用語
確率 : 2 項累積確率
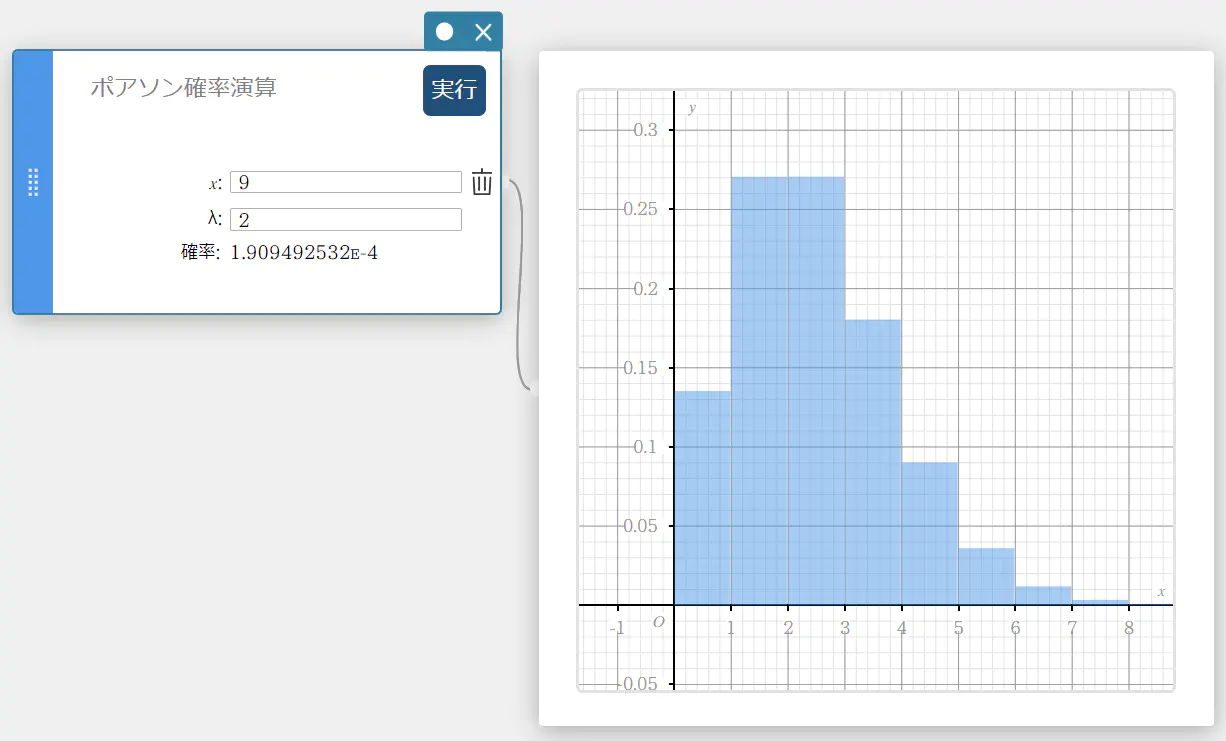
ポアソン確率演算 
指定された試行において成功するポアソン分布の確率を求めます。
\(f(x)=\displaystyle\frac{e^{-\lambda} \lambda^x}{x!} \qquad (x=0,1,2,\cdots)\)
- 入力値の用語
\( x \) : 指定試行値 (整数、 \(x \ge 0\))
\( \lambda \) : 平均(\(\lambda \gt 0\)) -
出力値の用語
確率 : ポアソン確率
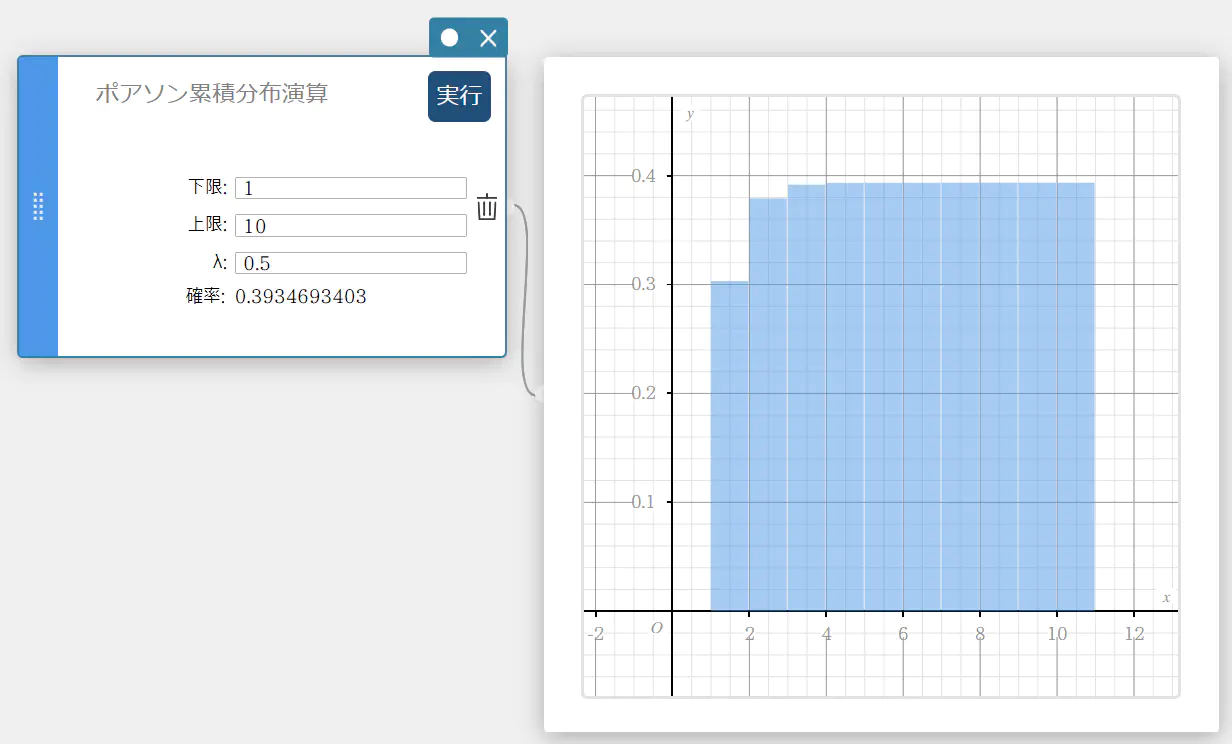
ポアソン累積分布演算 
指定された範囲において成功する、ポアソン分布の累積確率を求めます。
- 入力値の用語
下限 : 下端
上限 : 上端
\( \lambda \) : 平均(\(\lambda \gt 0\)) -
出力値の用語
確率 : ポアソン累積確率
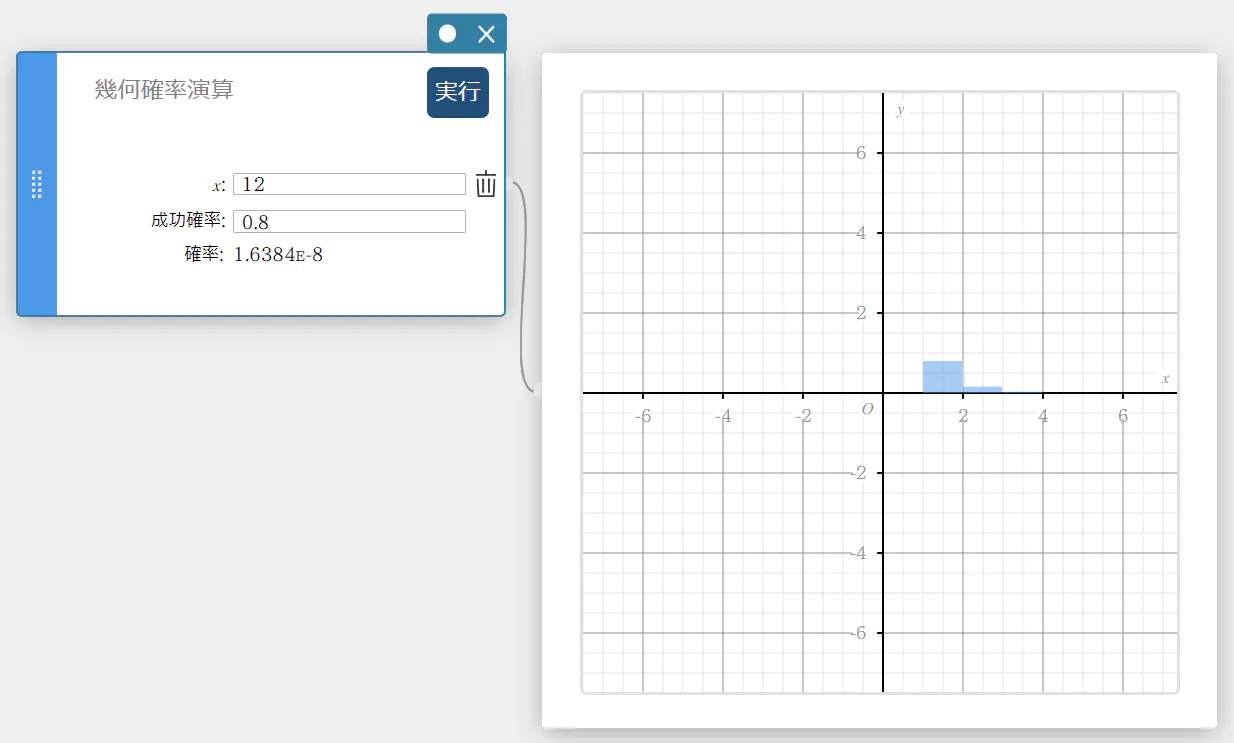
幾何確率演算 
指定された試行において成功する幾何分布の確率を求めます。
\( f(x)=p(1-p)^{x-1} \qquad (x=1,2,3,\cdots) \)
- 入力値の用語
\( x \) : 指定試行値(正の整数)
成功確率 : 成功確率 \(p\) (\(0 \le p \le 1\)) -
出力値の用語
確率 : 幾何確率
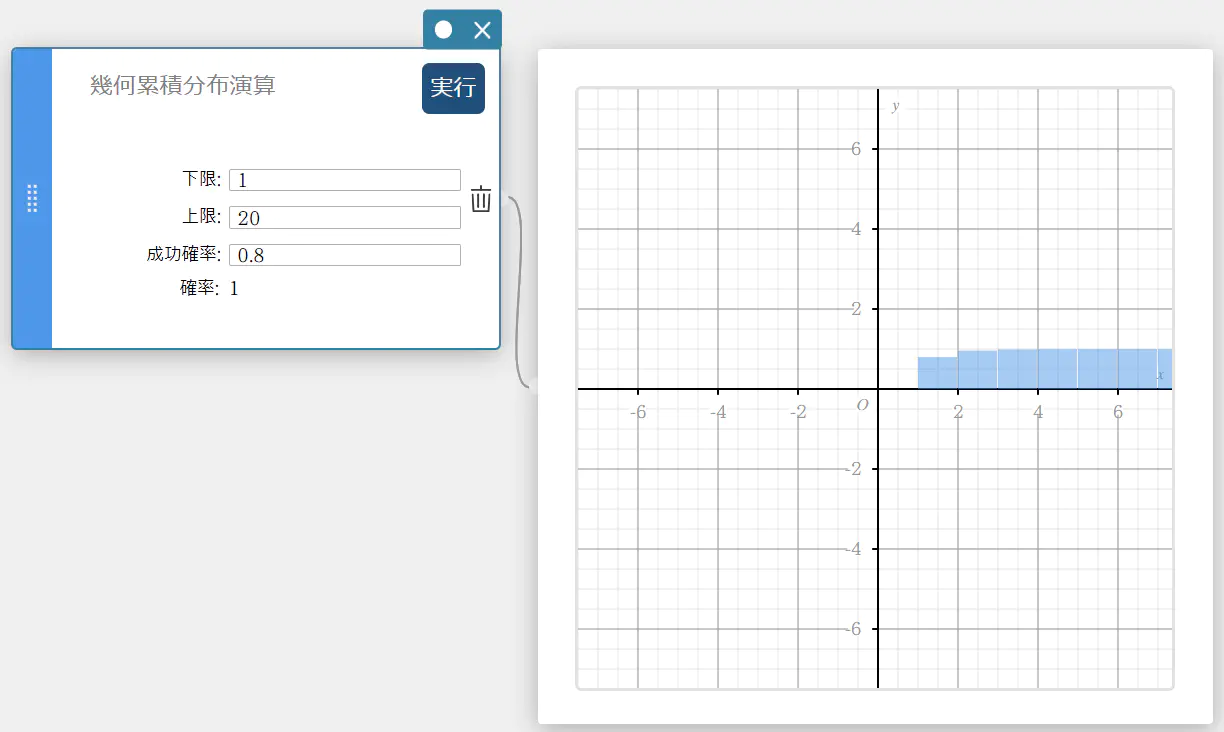
幾何累積分布演算 
指定された範囲において成功する、幾何分布の累積確率を求めます。
- 入力値の用語
下限 : 下端
上限 : 上端
成功確率 : 成功確率 \(p\)(\(0 \le p \le 1\)) -
出力値の用語
確率 : 幾何累積確率
超幾何確率演算 
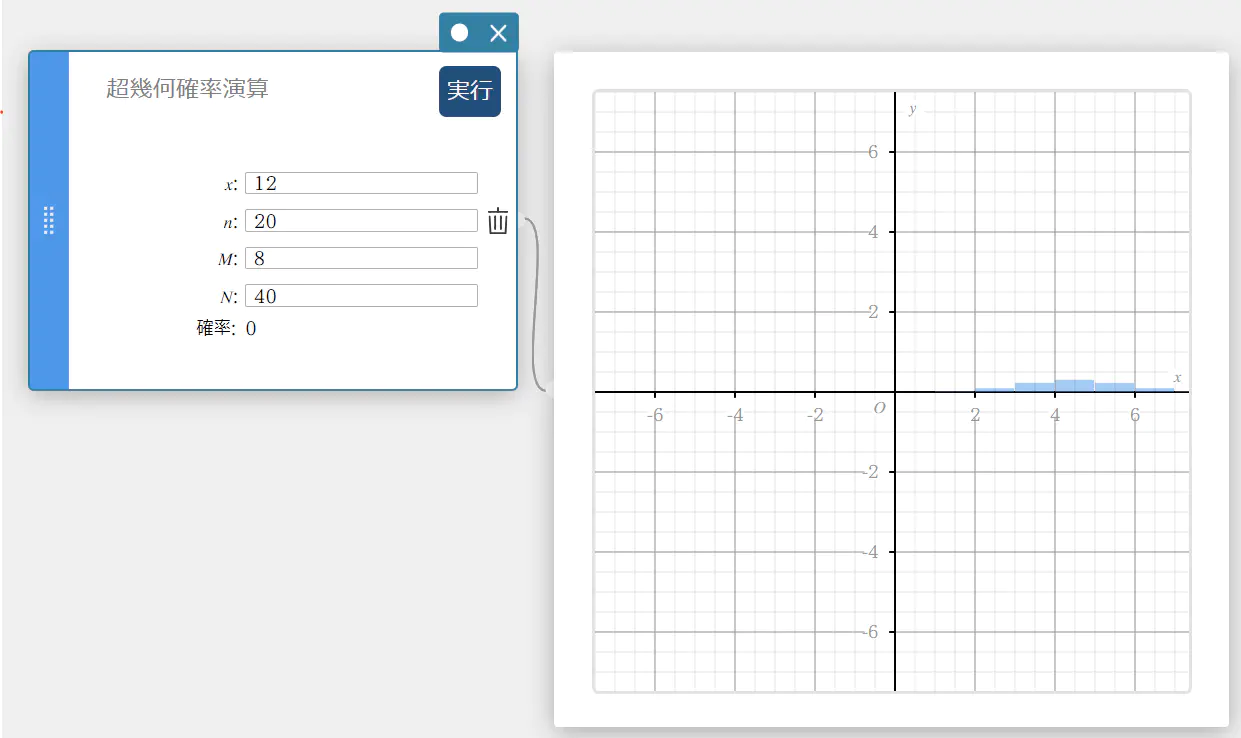
指定された範囲において成功する超幾何分布の確率を求めます。
\( prob = \displaystyle\frac{ {}_MC_x \times {}_{N-M}C_{n-x} }{ {}_NC_n } \)
- 入力値の用語
\(x\) : 指定試行値(整数)
\(n\) : 母集団からの抽出要素数(\(0 \le n\) 整数)
\(M\) : 母集団における成功数(\(0 \le M\) 整数)
\(N\) : 母集団要素数(\(n \le N\)、\(M \le N\) 整数) -
出力値の用語
確率 : 超幾何確率
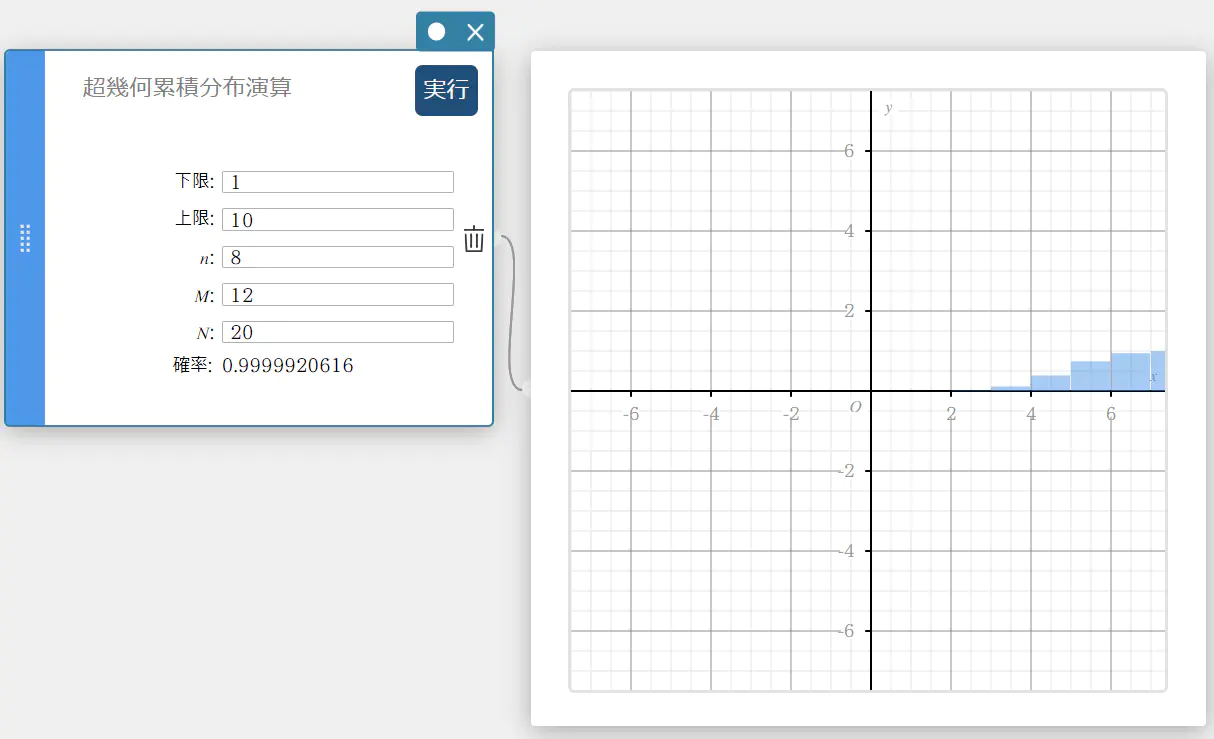
超幾何累積分布演算 
指定された範囲において成功する、超幾何分布の累積確率を求めます。
\( prob = \sum_{i=Lower}^{Upper}\displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)
- 入力値の用語
下限 : 下端
上限 : 上端
\(n\) : 母集団からの抽出要素数(\(0 \le n\) 整数)
\(M\) : 母集団における成功数(\(0 \le M\) 整数)
\(N\) : 母集団要素数(\(n \le N\)、\(M \le N\) 整数) -
出力値の用語
確率 : 超幾何累積確率
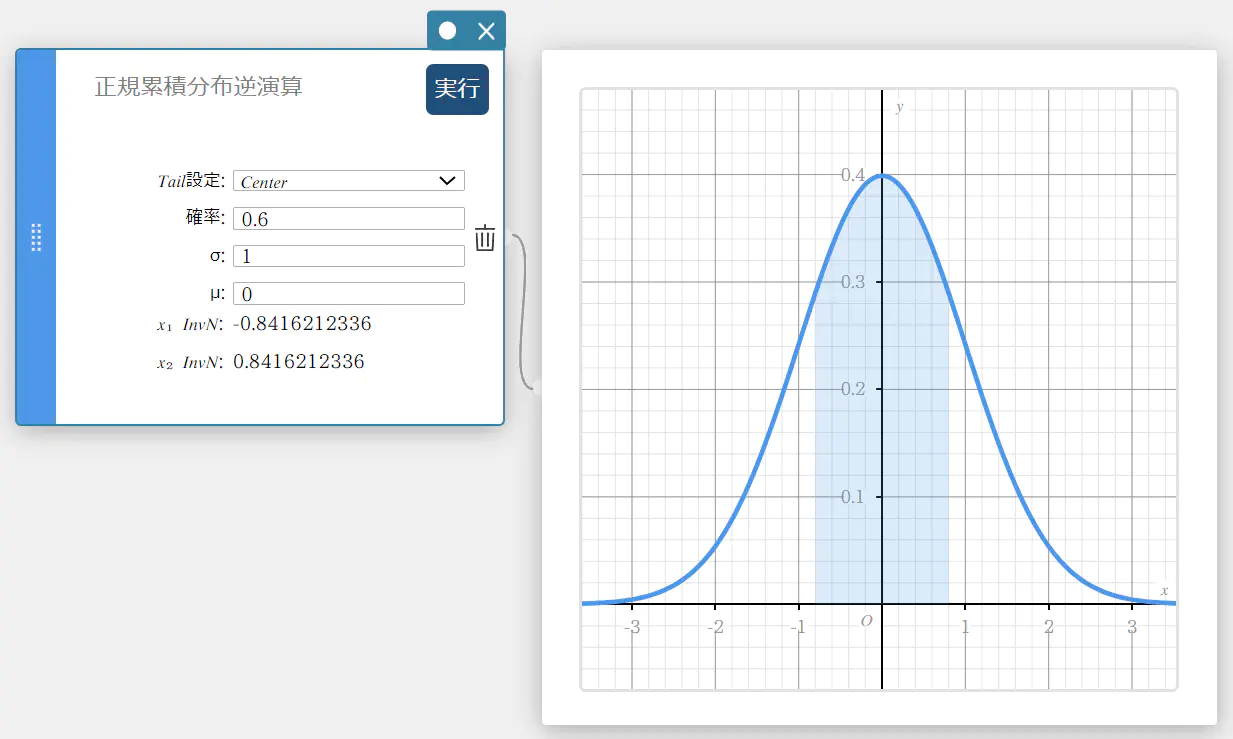
正規累積分布逆演算 
指定された確率値に対する、正規累積確率分布の境界値(上端と下端)を求めます。
Tail: Left の場合
\( \int_{-\infty}^{\alpha}f(x)dx=p \)
上端 \(\alpha\) が返されます。
Tail: Right の場合
\( \int_{\alpha}^{+\infty}f(x)dx=p \)
下端 \(\alpha\) が返されます。
Tail: Center の場合
\( \int_{\alpha}^{\beta}f(x)dx=p \qquad \left( \mu=\displaystyle\frac{\alpha+\beta}{2} \right) \)
下端 \(\alpha\) と上端 \(\beta\) が返されます。
- 入力値の用語
Tail 設定 : 確率値のTail 設定(Center、Left、Right)
確率 : 確率値(\(0 \le\) Area \(\le 1\))
\( \sigma \) : 母標準偏差(\( \sigma > 0 \))
\( \mu \) : 母平均 -
出力値の用語
\(x_1 {\rm InvN}\) : 上端(Tail 設定: Left)
下端(Tail 設定: Right または Center)
\(x_2 {\rm InvN}\) : 上端(Tail 設定: Center)
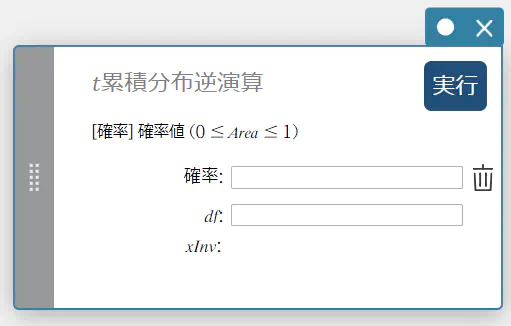
\(t\) 累積分布逆演算 
指定された確率値に対する、スチューデントの \(t\) 累積確率分布の下端値を求めます。
\( \int_{\alpha}^{+\infty}f(x)=p \)
- 入力値の用語
確率 : \(t\) 累積確率(\(0 \le\) Area \(\le 1\))
\(df\) : 自由度(\(df \gt 0\)) -
出力値の用語
\(x {\rm Inv}\) : \(t\) 累積確率分布の下端
\(\chi^2\) 累積分布逆演算 
指定された確率値に対する、 \(\chi^2\) 累積確率分布の下端値を求めます。
\( \int_{\alpha}^{+\infty}f(x)=p \)
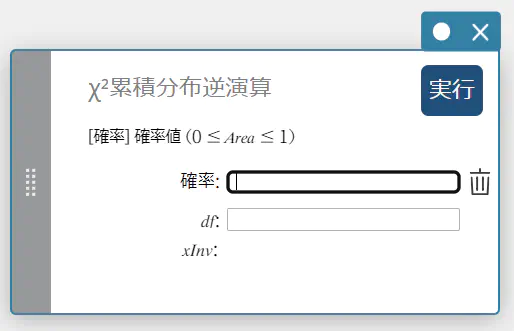
- 入力値の用語
確率 : \(\chi^2\) 累積確率(\(0 \le\) Area \(\le 1\))
\(df\) : 自由度(正の整数) -
出力値の用語
\(x {\rm Inv}\) : \(\chi^2\) 累積確率分布の下端
F 累積分布逆演算 
指定された確率値に対する、F 累積確率分布の下端値を求めます。
\( \int_{\alpha}^{+\infty}f(x)=p \)
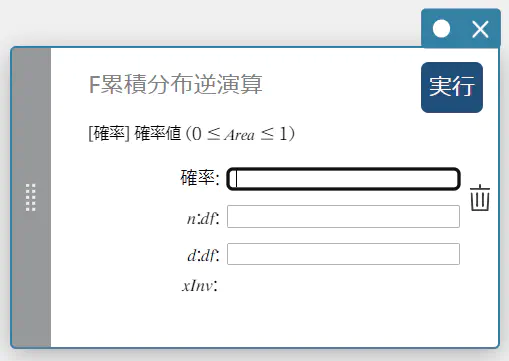
- 入力値の用語
確率 : F 累積確率(\(0 \le\) Area \(\le 1\))
\(n:df\) : 分子の自由度(正の整数)
\(d:df\) : 分母の自由度(正の整数) -
出力値の用語
\(x {\rm Inv}\) : F 累積確率分布の下端
2 項累積分布逆演算 
指定された確率値に対する、2 項累積確率分布の最小試行回数(上端値)を求めます。
\( \sum_{x=0}^{m}f(x)\ge prob \)
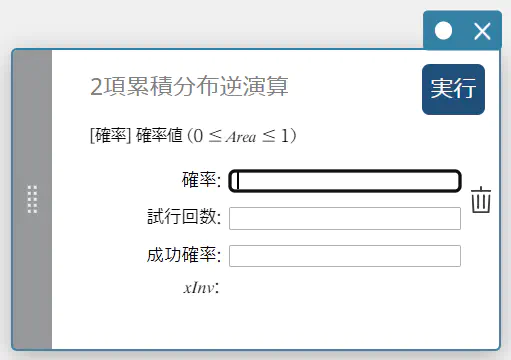
- 入力値の用語
確率 : 2 項累積確率(\(0 \le\) Area \(\le 1\))
試行回数 : 試行回数 \(n\)(整数、\(n \ge 0\))
成功確率 : 成功確率 \(p\)(\(0 \le p \le 1\)) -
出力値の用語
\(x {\rm Inv}\) : 2 項累積確率分布の最小試行回数(上端値)
ポアソン累積分布逆演算 
指定された確率値に対する、ポアソン累積確率分布の最小試行回数(上端値)を求めます。
\( \sum_{x=0}^{m}f(x)\ge prob \)
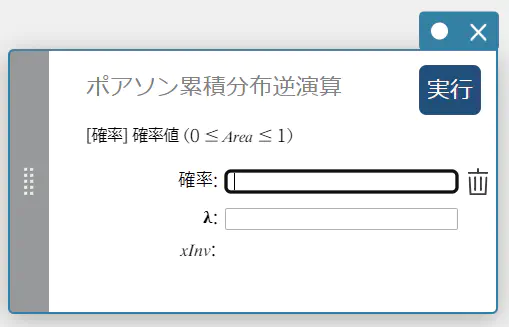
- 入力値の用語
確率 : ポアソン累積確率(\(0 \le\) Area \(\le 1\))
\( \lambda \) : 平均(\(\lambda \gt 0\)) -
出力値の用語
\(x {\rm Inv}\) : ポアソン累積確率分布の最小試行回数(上端値)
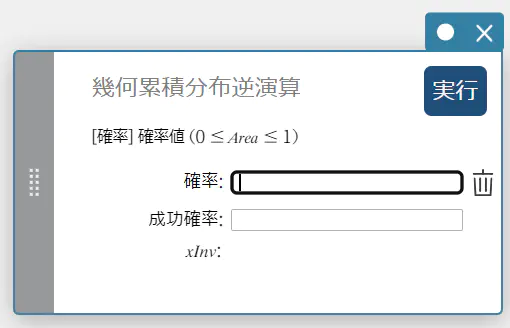
幾何累積分布逆演算 
指定された確率値に対する、幾何累積確率分布の最小試行回数を求めます。
\( \sum_{x=0}^{m}f(x)\ge prob \)
- 入力値の用語
確率 : 幾何累積確率(\(0 \le\) Area \(\le 1\))
成功確率 : 成功確率 \(p\)(\(0 \le p \le 1\)) -
出力値の用語
\(x {\rm Inv}\) : 幾何累積確率分布の最小試行回数(上端値)
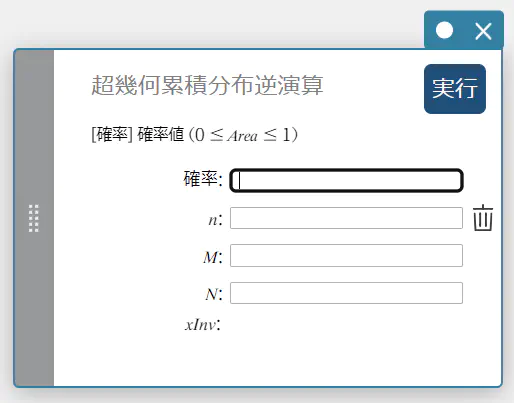
超幾何累積分布逆演算 
指定された確率値に対する、超幾何累積確率分布の最小試行回数(上端値)を求めます。
\( prob \le \sum_{i=0}^{X} \displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)
- 入力値の用語
確率 : 超幾何累積確率(\(0 \le\) Area \(\le 1\))
\(n\) : 母集団からの抽出要素数(\(0 \le n\) 整数)
\(M\) : 母集団における成功数(\(0 \le \rm M\) 整数)
\(N\) : 母集団要素数(\(n \le \rm N, \rm M \le \rm N\) 整数) -
出力値の用語
\(x {\rm Inv}\): 超幾何累積確率分布の最小試行回数(上端値)
各種グラフ描画
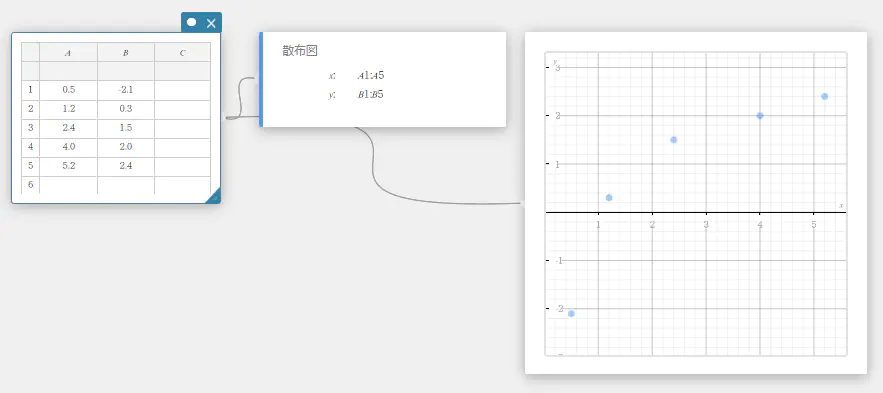
散布図
このグラフでは、データの累積比率を正規分布の累積比率と比較できます。散布図が直線に近ければ、ほぼ正規分布に近いことがわかります。直線から外れるほど、正規分布から外れていることを表します。
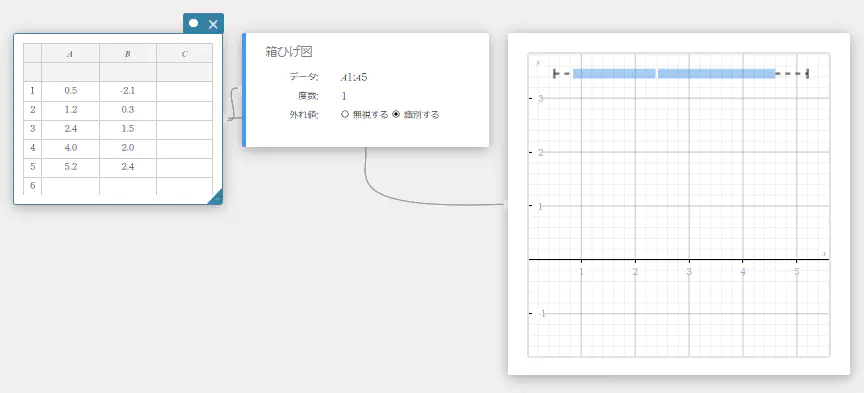
箱ひげ図
このグラフでは、多くのデータが特定の範囲内にどのように収まっているかを確認できます。データの第 1 四分位数(\({\rm Q}_1\))からデータの第 3 四分位数(\({\rm Q}_3\))までがボックスで囲まれ、中央値(\({\rm Med}\))の地点に線が引かれます。ボックスの両端から、データの最小値(\({\rm minX}\))と最大値(\({\rm maxX}\))へ向かって線(ひげ)が描かれます。
ヒストグラム
ヒストグラムは、各データクラスの度数(度数分布)を、長方形の棒で表示します。クラスは横軸、度数は縦軸になります。必要に応じて、ヒストグラムの開始値(開始区間)とステップ値(間隔)を変更することができます。
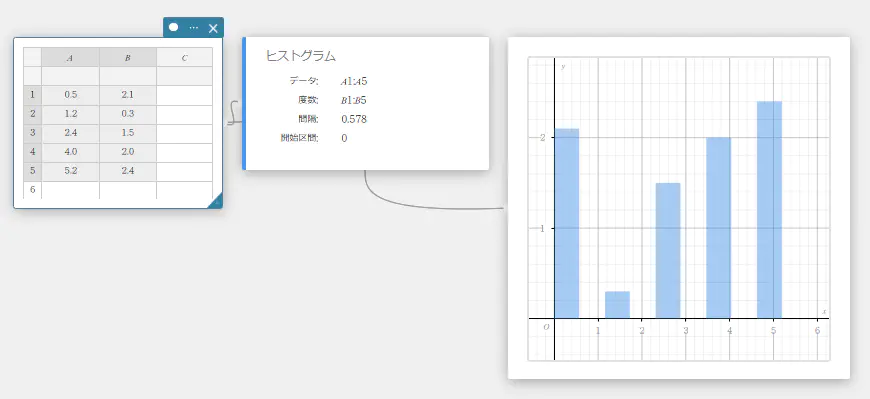
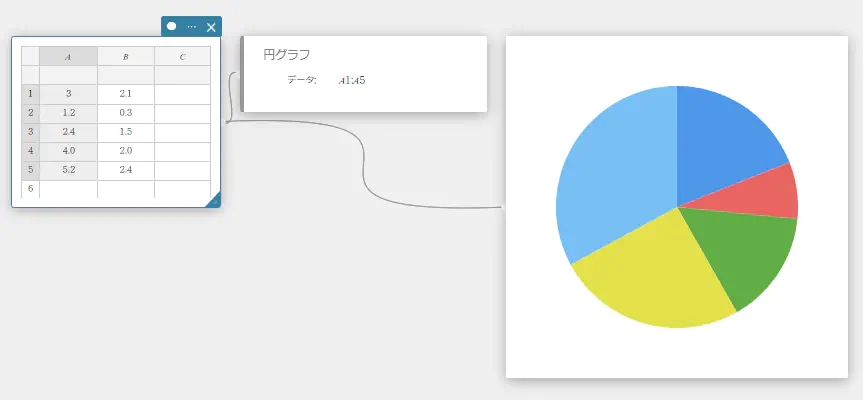
円グラフ
リストデータに基づいて円グラフを描きます。
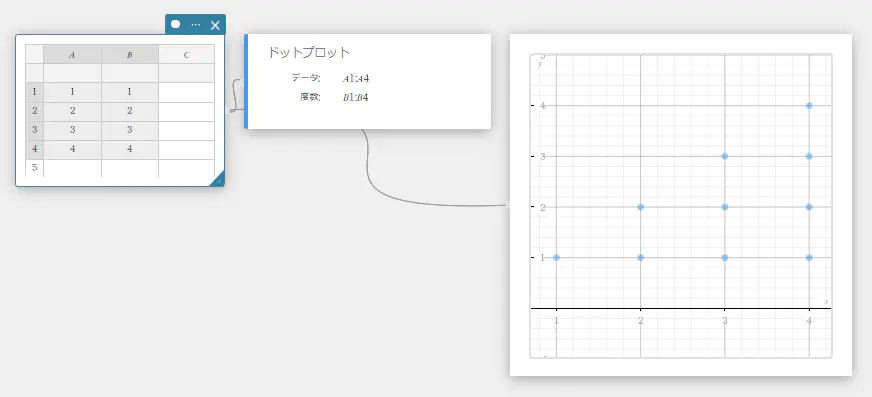
ドットプロット
列 A(横軸)の数値はデータ番号を表し、列 B(縦軸)は各データの度数を表します。縦軸には、データごとに 1度数につき 1つのドットがプロットされます。