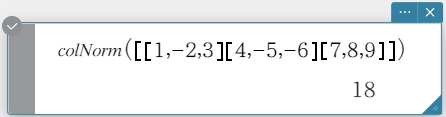Matrix

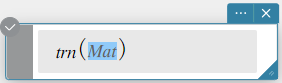
trn

Returns a transposed matrix.
Syntax: trn (Mat [ ) ]

augment

Returns a matrix that combines two other matrices.
Syntax: augment (Mat-1, Mat-2 [ ) ]

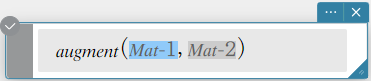
ident

Creates an identity matrix.
Syntax: ident (natural number [ ) ]

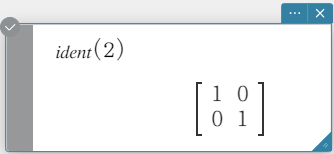
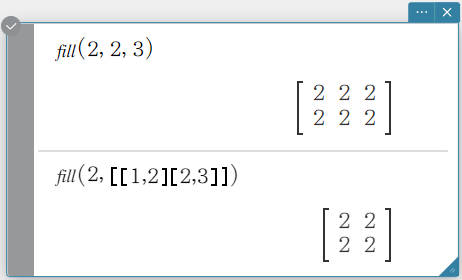
fill

Creates a matrix with a specific number of rows and columns, or replaces the elements of a matrix with a specific expression.
Syntax:
fill (Exp, number of rows, number of columns [ ) ]
　　 fill (Exp, Mat [ ) ]

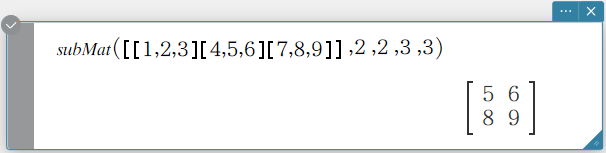
subMat

Extracts a specific section of a matrix into a new matrix.
Syntax: subMat (Mat [, start row] [, start column] [, end row] [, end column] [ ) ]

• “1” is the default when you omit “[, start row]” and “[, start column]”.
• The last row number is the default when you omit “[, end row]”.
• The last column number is the default when you omit “[, end column]”.

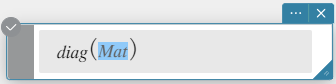
diag

Returns a one-row matrix containing the elements from the main diagonal of a square matrix.
Syntax: diag (Mat[ ) ]

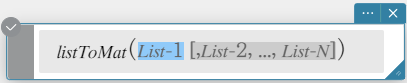
listToMat

Transforms lists into a matrix.
Syntax: listToMat (List-1 [, List-2, …, List-N] [ ) ]

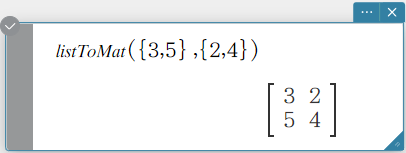
matToList

Transforms a specific column of a matrix into a list.

Syntax: matToList (Mat, column number [ ) ]

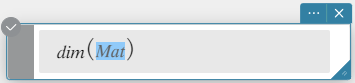
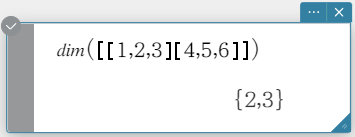
dim

Returns the dimensions of a matrix as a two-element list {number of rows, number of columns}.
Syntax: dim (Mat [ ) ]

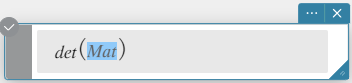
det

Returns the determinant of a square matrix.
Syntax: det (Mat [ ) ]

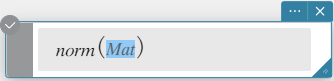
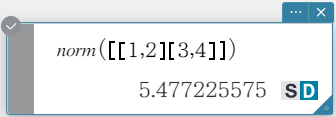
norm

Returns the Frobenius norm of the matrix.
Syntax: norm (Mat [ ) ]

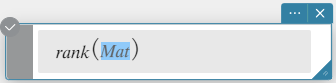
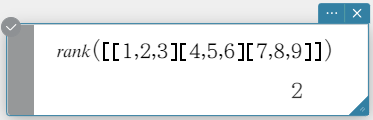
rank

Finds the rank of matrix. The rank function computes the rank of a matrix by performing Gaussian elimination on the rows of the given matrix. The rank of matrix A is the number of non-zero rows in the resulting matrix.
Syntax: rank (Mat [ ) ]

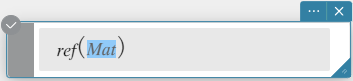
ref

Returns the row echelon form of a matrix.
Syntax: ref (Mat [ ) ]

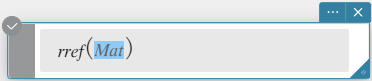
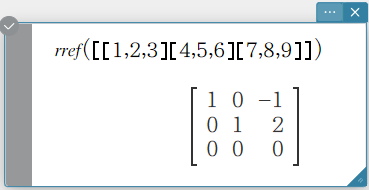
rref

Returns the reduced row echelon form of a matrix.
Syntax: rref (Mat [ ) ]

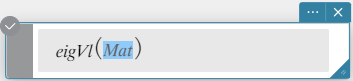
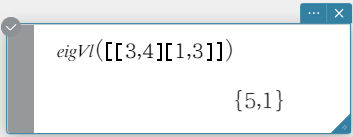
eigVl

Returns a list that contains the eigenvalue(s) of a square matrix.
Syntax: eigVl (Mat [ ) ]

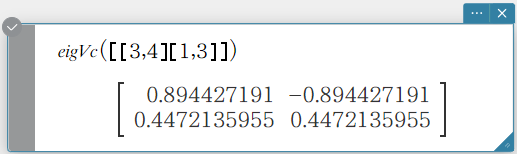
eigVc

Returns a matrix in which each column represents an eigenvector of a square matrix.

• Since an eigenvector usually cannot be determined uniquely, it is standardized as follows to its norm, which is 1:
  　When \({\rm V} = [ x_1, x_2, …, x_n ]\), \(\sqrt{\left( |x_1|^2+|x_2|^2+…+|x_n|^2 \right)}=1.\).
  Syntax: eigVc (Mat [ ) ]

LU

Returns the LU decomposition of a square matrix.
Syntax: LU (Mat, lVariableMem, uVariableMem [ ) ]

• The lower matrix is assigned to the first variable L, while the upper matrix is assigned to the second variable U.

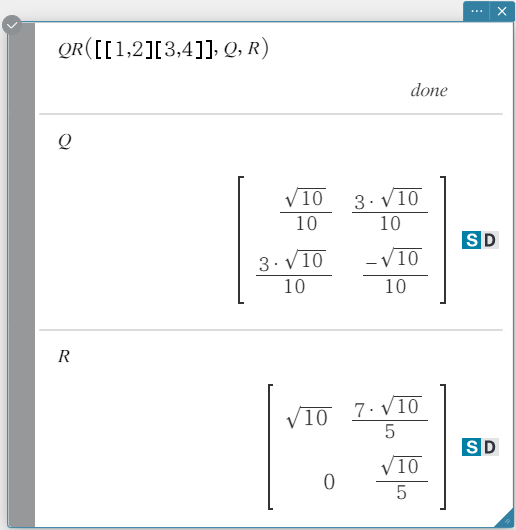
QR

Returns the QR decomposition of a square matrix.
Syntax: QR (Mat, qVariableMem, rVariableMem [ ) ]
Example: To obtain the QR decomposition of the matrix [[1, 2] [3, 4]]

• The unitary matrix is assigned to variable Q, while the upper triangular matrix is assigned to variable R.

swap

Swaps two rows of a matrix.
Syntax: swap (Mat, row number-1, row number-2 [ ) ]

mRow

Multiplies the elements of a specific row in a matrix by a specific expression.
Syntax: mRow (Exp, Mat, row number [ ) ]

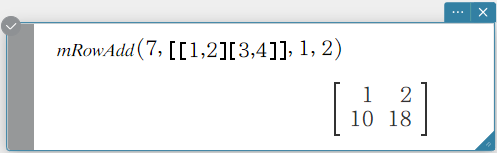
mRowAdd

Multiplies the elements of a specific row in a matrix by a specific expression, and then adds the result to another row.
Syntax: mRowAdd (Exp, Mat, row number-1, row number-2 [ ) ]

rowAdd

Adds a specific matrix row to another row.
Syntax: rowAdd (Mat, row number-1, row number-2 [ ) ]

rowDim

Returns the number of rows in a matrix.
Syntax: rowDim (Mat [ ) ]

rowNorm

Calculates the sums of the absolute values of the elements of each row of a matrix, and returns the maximum value of the sums.
Syntax: rowNorm (Mat [ ) ]

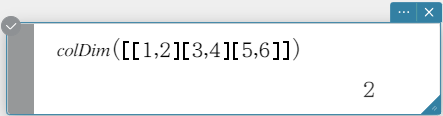
colDim

Returns the number of columns in a matrix.
Syntax: colDim (Mat [ ) ]

colNorm

Calculates the sums of the absolute values of the elements of each column of a matrix, and returns the maximum value of the sums.
Syntax: colNorm (Mat [ ) ]