Financial

You can use the Financial sticky note to perform a variety of financial calculations.

Important
Financial calculation rules and practices can differ according to country, geographic area, or financial institution. It is up to you to determine whether the calculation results produced by the Financial sticky note are compatible with the financial calculation rules that apply to you.

table of contents

Financial Calculation Basic Operations
Configuring Financial Settings
Simple Interest
Compound Interest
Cash Flow
Amortization
Interest Conversion
Cost/Sell/Margin
Day Count
Depreciation
Bond Calculation
Break-Even Point
Margin of Safety
Operating Leverage
Financial Leverage
Combined Leverage
Quantity Conversion

Financial Calculation Basic Operations

To select the type of Financial Calculation

1. Click in the sticky note menu.
   
   This creates a Financial sticky note and displays a financial calculation type list.
   You can switch between page 1 and page 2 of the type list by clicking [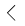] or [].
   
2. Click a financial calculation type.
   This switches to a Financial sticky note of the type you clicked. For example, clicking [Simple Interest] switches to a Simple Interest sticky note.

• Financial Calculation Example
  This section uses a Simple Interest sticky note to show basic financial calculation operations.

Example: What is the final value after two years (730 days) of a $3,000 investment earning 5% simple interest? Also calculate the final value during the same period for the same investment when the simple interest rate is 3%.

1. Click in the sticky note menu.
   This creates a Financial sticky note and displays a financial calculation type list.
2. Click [Simple Interest].
   This displays the Simple Interest sticky note.
   
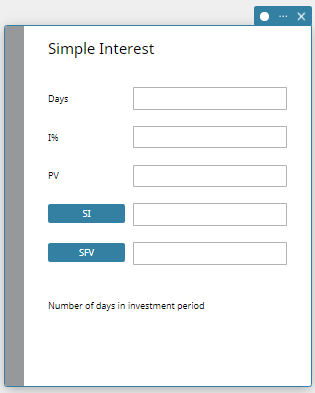
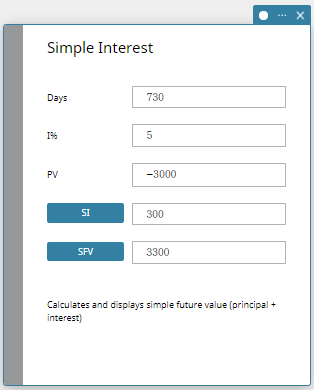
3. Input the following information:
   Days\(=730\)
   I%（annual interest rate）\(=5\)
   PV（present value）\(=-3000\)
4. Click [SI] and then [SFV].
   This displays the calculation results for simple interest (SI) and simple future value (SFV = principal + interest).
   
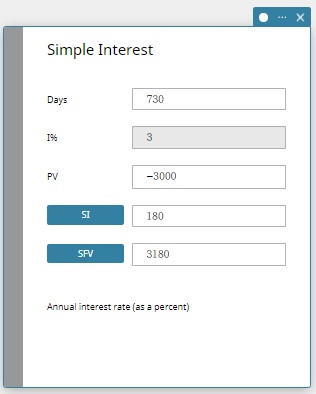
5. Change the I% value to \(3\), click [SI], and then [SFV].
   The SI and SFV values are updated in accordance with the new I% value.
   

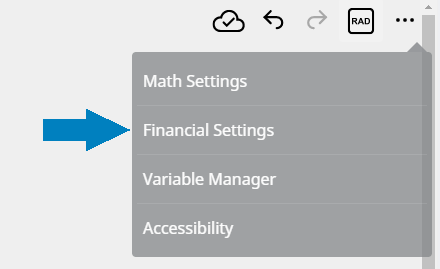
Configuring Financial Settings

1. Click in the right end of the Paper header.
   
2. Click [Financial Settings].
   
   This displays the Financial Settings dialog box.
   
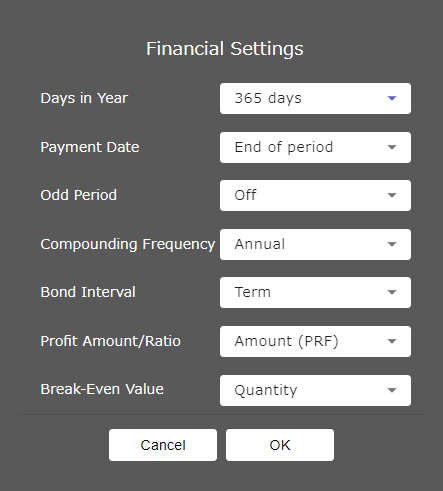
3. You can use this screen to configure settings below.
   Days in Year
   　　360 days: Specifies calculation according to a 360 days.
   　　365 days: Specifies calculation according to a 365 days.
   Payment Date
   　　Beginning of period: Specifies the beginning of period as the payment date.
   　　End of period: Specifies the end of period as the payment date.
   Odd Period
   　　Compound (CI): Specifies compound interest to the odd period when performing a Compound Interest calculation.
   　　Simple (SI): Specifies simple interest to the odd period when performing a Compound Interest calculation.
   　　Off: Specifies no interest to the odd period when performing a Compound Interest calculation.
   Compounding Frequency
   　　Annual: Specifies once a year compounding.
   　　Semi-annual: Specifies twice a year compounding.
   Bond Interval
   　　Term: Uses a number of payments as the term for bond calculation.
   　　Date: Uses a date as the term for bond calculation.
   Profit Amount/Ratio
   　　Amount (PRF): Uses amount (PRF) for break-even point calculations.
   　　Ratio (r%): Uses profit ratio (r%) for break-even point calculations.
   Break-Even Value
   　　Quantity: Uses quantity for break-even point calculations.
   　　Sales: Uses sales amount for break-even point calculations.
4. Click [OK].
   This applies the settings.
   
   MEMO
   Initial default settings are shown below.
   Days in Year: 365 days
   Payment Date: End of period
   Odd Period: Off
   Compounding Frequency: Annual
   Bond Interval: Amount (PRF)
   Break-Even Value: Quantity

• The table below shows setting items for each type of Financial calculation.

Financial Calculation	Setting Items
Simple Interest	Days in Year
Compound Interest	Payment Date, Odd Period
Amortization	Payment Date
Day Count	Days in Year
Bond Calculation	Days in Year, Compounding Frequency, Bond Interval
Break-Even Point	Profit Amount/Ratio, Break-Even Value

• There are two ways to change financial settings.
  － Change the settings by clicking in a Financial sticky note.
  
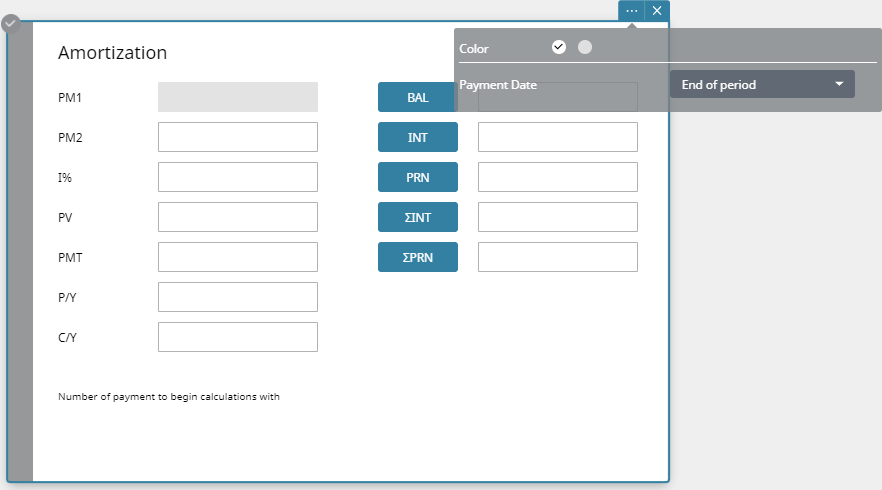
  － Change the settings by clicking [Financial Settings] from in the Paper header.
  
  Setting changes made from are only applied to the Financial Sticky Note being changed.
  Setting changes made from [Financial Settings] are applied to all Financial sticky notes created after the changes were made. The setting changes are not applied to Financial sticky notes created before the changes were made.

Simple Interest

Simple Interest lets you calculate interest (without compounding) based on the number of days money is invested.

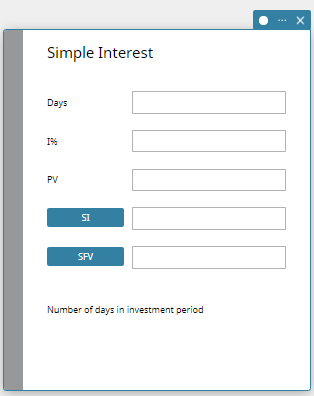
• Simple Interest Fields
  The following fields appear on the Simple Interest calculation.

Field	Description
Days	Number of days in investment period
I%	Annual interest rate (as a percent)
PV	Present value (initial investment)
SI	Calculates and displays simple interest
SFV	Calculates and displays simple future value (principal + interest)

Calculation Formulas

• 365-day Mode
  

\( SI^′ =\displaystyle \frac{Days}{365}\times{PV}\times{i} \qquad \left( i=\displaystyle\frac{I\%}{100} \right) \)

• 360-day Mode
  

\( SI^′ = \displaystyle\frac{Days}{360}\times{PV}\times{i} \qquad \left( i=\displaystyle\frac{I\%}{100} \right) \)
\( SI = -SI^′ \)
\( SFV = -(PV + SI^′) \)

Compound Interest

Compound Interest lets you calculate interest based on compounding parameters you specify.

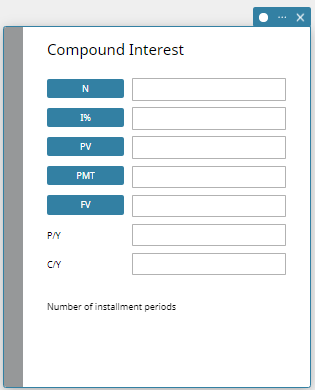
• Compound Interest Fields
  The following fields appear on the Compound Interest calculation.

Field	Description
N	Number of installment periods
I%	Annual interest rate (as a percent)
PV	Present value (initial investment)
PMT	Amount paid each period
FV	Future value
P/Y	Number of installment periods per year
C/Y	Number of times interest is compounded per year

Calculation Formulas

• When calculating PV, PMT, FV, n
  

　\( I \% \ne 0 \)
　\( PV = \displaystyle\frac{-\alpha\times{PMT}-\beta\times{FV}}{\gamma} \)
　\( PMT = \displaystyle\frac{-\gamma\times{PV}-\beta\times{FV}}{\alpha} \)
　\( FV = \displaystyle\frac{-\gamma\times{PV}-\alpha\times{PMT}}{\beta} \)
　\( n = \displaystyle\frac{log\left\{\displaystyle\frac{(1+iS)\times{PMT}-FV\times{i}}{(1+iS)\times{PMT}+PV\times{i}}\right\}}{\log{(1+i)}} \)


\( I \% = 0 \)
　\( PV = -(PMT\times{n}+FV) \)
　\( PMT = -\displaystyle\frac{PV + FV}{n} \)
　\( FV = -(PMT\times{n}+PV) \)
　\( n = -\displaystyle\frac{PV+FV}{PMT} \)

　\( \alpha=(1+i\times{S})\times\displaystyle\frac{1-\beta}{i} \)

When “Odd Period” is “Off”

\(\beta=\)\(\left(1+i\right)^{-n}\)

\(\gamma=\)\(1\)

When “Odd Period” is “CI”

\(\beta=\)\(\left(1+i\right)^{-Ing\left(n\right)}\)

\(\gamma=\)\(\left(1+i\right)^{Frac\left(n\right)}\)

When “Odd Period” is “SI”

\(\beta=\)\(\left(1+i\right)^{-Ing\left(n\right)}\)

\(\gamma=\)\(1+i \times{Frac\left(n\right)}\)

When “Payment Date” is “End of period”

\(S=\)\(0\)

When “Payment Date” is “Beginning of period”

\(S=\)\(1\)

When \(P/Y = C/Y = 1\)

\(i=\)\( \displaystyle\frac{I \%}{100} \)

When \(P/Y \neq 1\) and/or \(C/Y \neq 1\)

\(i=\)\( {\left(1+\displaystyle\frac{I\%}{100\times\left[C/Y \right]}\right)}^{\displaystyle\frac{C/Y}{P/Y}}-1 \)

• When calculating \(I \%\)
  \(i\) (effective interest rate) is calculated using Newton’s Method.
  \( \gamma\times{PV}+\alpha\times{PMT}+\beta\times{FV}=0\)
  \( I \) % is calculated from i using the formulas below:

When \(P/Y = C/Y = 1\)

\( I \% = \)\( i\times{10} \)

When \(P/Y \neq 1\) and/or \( C/Y \neq 1\)

\( I \% = \)\( \left( {\left( 1+i \right) }^{\displaystyle\frac{P/Y}{C/Y}}-1 \right) \times C/Y \times{100} \)

Interest (\(I\%\)) is calculated using Newton’s Method, which produces approximate values whose precision can be affected by various calculation conditions. Interest calculation results produced by this application should be used keeping the above in mind, or results should be confirmed separately.

Cash Flow

Cash Flow lets you calculate the value of money paid out or received in varying amounts over time.

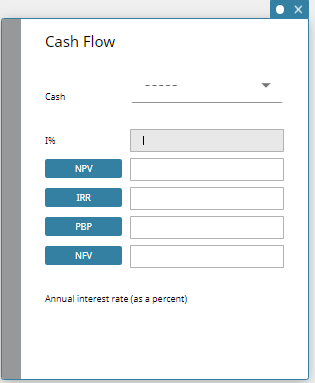
• Cash Flow Fields
  The following fields appear on the Cash Flow calculation.

Field	Description
Cash	List of income or expenses (up to 80 entries)
I%	Annual interest rate (as a percent)
NPV	Net present value
IRR	Interest rate of return
PBP	Payback period
NFV	Net future value

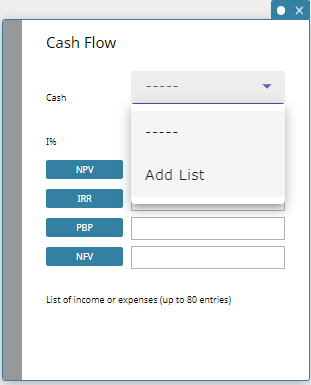
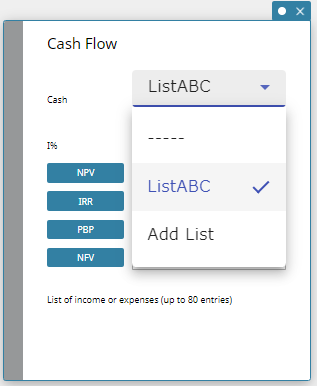
• To specify the list to be used by Cash Flow

1. On the Cash Flow sticky note, click the “Cash” field.
2. On the menu that appears, click “Add List”.
   This displays a Data sticky note.
   
3. Enter the data to be used by Cash Flow into the Data sticky note.
   
4. Input the list name at the top of data you input.
   
5. On the Cash Flow sticky note, click the “Cash” field.
6. On the menu that appears, select the list to be used by Cash Flow.
   
   MEMO
   For more information about how to edit data values on a Data sticky note, see “Editing Statistical Data Values”.
   When a variable is defined as a list type variable, it will appear in the “Cash” field pulldown menu. You can use a list type variable to perform Cash Flow calculations. For more information about variable types, see “Using Variable Manager”.

Calculation Formulas

\( NPV=CF_{0}+\displaystyle\frac{CF_{1}}{\left(1+i\right)}+\displaystyle\frac{CF_{2}}{{\left(1+i\right)}^{2}}+\displaystyle\frac{CF_{3}}{{\left(1+i\right)}^{3}}+ \cdots +\displaystyle\frac{CF_{n}}{{\left(1+i\right)}^{n}} \qquad \left(i=\displaystyle\frac{I\%}{100}\right) \)

\( n \): natural number up to 80
\( NFV=NPV\times{\left(1+i\right)}^{n} \)

IRR is calculated using Newton’s Method.

\( 0=CF_{0}+\displaystyle\frac{CF_{1}}{\left(1+i\right)}+\displaystyle\frac{CF_{2}}{{\left(1+i\right)}^{2}}+\displaystyle\frac{CF_{3}}{{\left(1+i\right)}^{3}}+ \cdots +\displaystyle\frac{CF_{n}}{{\left(1+i\right)}^{n}} \)

In this formula, NPV = 0, and the value of IRR is equivalent to i×100. It should be noted, however, that minute fractional values tend to accumulate during the subsequent calculations performed automatically, so NPV never actually reaches exactly zero. IRR becomes more accurate the closer that NPV approaches to zero.

\(
PBP=\begin{cases}
0　………………　\left(CF_{0}\geq0\right)\cr
n-\displaystyle\frac{NPV_{n}}{NPV_{n+1}-NPV_{n}}　…　{(Other　than　those　above)}
\end{cases}
\)
\( \displaystyle NPV_{n}=\sum_{k=0}^n\displaystyle\frac{CF_{k}}{{\left(1+i\right)}^k} \)

\( n \): Minimum positive integer that meets the conditions \( NPV_{n}\leq 0 \), \(0 \leq NPV_{n+1} \) or zero

Amortization

Amortization can be used to calculate the interest and principal paid for a particular year, the total interest and total interest paid for a certain period (year), and the outstanding principal.

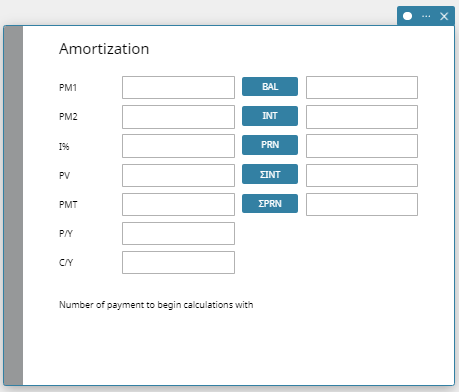
• Amortization Fields
  The following fields appear on the Amortization calculation.

Field	Description
PM1	Number of first installment period in interval under consideration
PM2	Number of last installment period in interval under consideration
I%	Annual interest rate (as a percent)
PV	Present value (initial investment)
PMT	Amount paid each period
P/Y	Number of installment periods per year
C/Y	Number of times interest is compounded per year
BAL	Balance of principal after PM2
INT	Interest portion of PM1
PRN	Principal portion of PM1
ΣINT	Total interest paid from PM1 to PM2 (inclusive)
ΣPRN	Total principal paid from PM1 to PM2 (inclusive)

Calculation Formulas

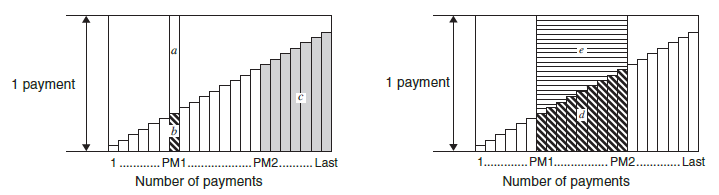
a: Interest portion of payment PM1 (INT)

　\( INT_{\rm PM1}=\mid{BAL_{\rm PM1-1} \times i}\mid\times\left(PMT_{\rm sign}\right) \)

b: Principal portion of payment PM1 (PRN)
　\(PRN_{\rm PM1}=PMT+BAL_{\rm PM1-1}\times{i}\)

c: Principal balance upon completion of payment PM2 (BAL)
　\(BAL_{\rm PM2}=BAL_{\rm PM2-1}+PRN_{\rm PM2}\)

d: Total principal paid from payment PM1 to payment PM2 (ΣPRN)
　\(\displaystyle \sum_{\rm PM1}^{\rm PM2}PRN=PRN_{\rm PM1}+PRN_{\rm PM1+1}+\) … \(+PRN_{\rm PM2}\)

e: Total interest paid from payment PM1 to payment PM2 (ΣINT)
　\(a + b =\) one repayment (PMT)

\(\displaystyle \sum_{\rm PM1}^{\rm PM2}INT=INT_{\rm PM1}+INT_{\rm PM1+1}+…+INT_{\rm PM2}\)

\(BAL_{0}=PV……………. \) Payment Date: End of period. (See “Configuring Financial Settings”.)

\(INT_{1}=0,PRN_{1}=PMT… \) Payment Date: Beginning of period. (See “Configuring Financial Settings”.)

Converting between the Nominal Interest Rate and Effective Interest Rate
The nominal interest rate (\(I\%\) value input by user) is converted to an effective interest rate ((\(I\%^′\))) for installment loans where the number of annual payments (P/Y) is different from the number of annual compounding calculation periods (C/Y).

　\( I\%^′=\left\{{\left(1+\displaystyle\frac{I\%}{100\times\left[C/Y\right]}\right)}^{\displaystyle\frac{\left[C/Y\right]}{\left[P/Y\right]}}-1\right\}\times100 \)

After conversion from the nominal interest rate to the effective interest rate, i is calculated using the formula below.
　\( i=I\%^′ \div 100 \)

Interest Conversion

Interest Conversion lets you calculate the effective or nominal interest rate for interest that is compounded multiple times during a year.

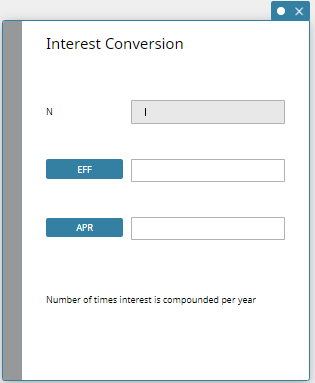
• Interest Conversion Fields
  The following fields appear on the Interest Conversion calculation.

Field	Description
N	Number of times interest is compounded per year
EFF	Effective interest rate (as a percent)
APR	Nominal interest rate (as a percent)

Calculation Formulas

\( EFF=\left[{\left(1+\displaystyle\frac{APR/100}{n}\right)}^{n}-1\right]\times100 \)
\( APR=\left[{\left(1+\displaystyle\frac{EFF}{100}\right)}^{\displaystyle\frac{1}{n}}-1\right]\times{n}\times100 \)

Cost/Sell/Margin

Cost/Sell/Margin lets you calculate the cost, selling price, or margin of profit on an item, given the other two values.

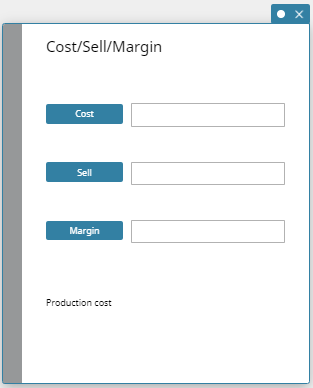
• Cost/Sell/Margin Fields
  The following fields appear on the Cost/Sell/Margin calculation.

Field	Description
Cost	Production cost
Sell	Selling price
Margin	Margin of profit (portion of selling price not absorbed by cost of production)

Calculation Formulas
\( CST=SEL\left(1-\displaystyle\frac{MRG}{100}\right) \)
\( SEL=\displaystyle\frac{CST}{1-\displaystyle\frac{MRG}{100}} \)
\( MRG\left(\%\right)=\left(1-\displaystyle\frac{CST}{SEL}\right)\times100 \)

Day Count

Day Count lets you calculate the number of days between two dates, or the date that is a specified number of days from another date.

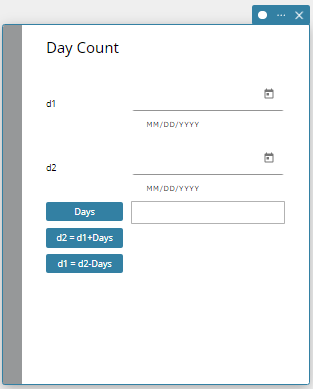
• Day Count Fields
  The following fields appear on the Day Count calculation.

Field	Description
d1	Date 1
d2	Date 2
Days	Number of days from d1 to d2

Depreciation

Depreciation lets you calculate the amount that a business expense can be offset by income (depreciated) over a given year.

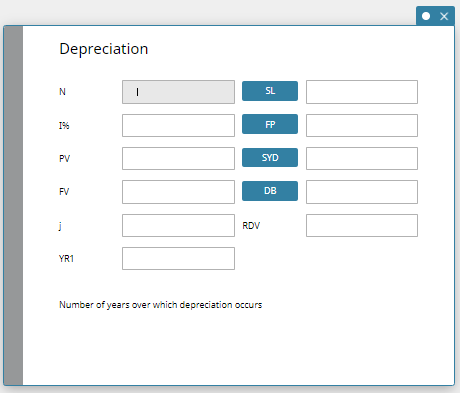
MEMO
You can also click [SL] to calculate depreciation using straight-line method, [FP] using fixed-percentage method, or [DB] using declining-balance method. Each depreciation method will produce a different residual value after depreciation (RDV) for the applicable year (j).

• Depreciation Fields
  The following fields appear on the Depreciation calculation.

Field	Description
N	Number of years over which depreciation occurs
I%	Depreciation rate (Fixed-Percentage Method or Declining-Balance Method)
PV	Present value (initial investment)
FV	Future value (residual value)
\(j\)	Year for which depreciation is being calculated
YR1	Number of depreciable months in first year
SL	Calculate depreciation for year \(j\) using the straight-line method
FP	Calculate depreciation for year \(j\) using the fixed-percentage method
SYD	Calculate depreciation for year \(j\) using the sum-of-the-years’-digits method
DB	Calculate depreciation for year \(j\) calculated using the declining-balance method
RDV	Residual value after depreciation for year \(j\)

Calculation Formulas

• Straight-Line Method
  

　\( SL_{1}=\displaystyle\frac{\left(PV-FV\right)}{n}\times\displaystyle\frac{YR1}{12} \)
　\( SL_{j}=\displaystyle\frac{\left(PV-FV\right)}{n} \)
　\( SL_{n+1}=\displaystyle\frac{\left(PV-FV\right)}{n}\times\displaystyle\frac{12-YR1}{12} \qquad \left(YR1\neq12\right) \)

• Fixed-Percentage Method
  　\( FP_{1}= PV\times\displaystyle\frac{I\%}{100}\times\displaystyle\frac{YR1}{12} \)
  　\( FP_{j}=\left(RDV_{j-1}+FV\right)\times\displaystyle\frac{I\%}{100} \)
  　\( FP_{n+1}=RDV_{n} \qquad \left(YR1\neq12\right) \)
  　\( RDV_{1}=PV-FV-FP_{1} \)
  　\( RDV_{j}=RDV_{j-1}-FP_{j} \)
  　\( RDV_{n+1}=0 \qquad \left(YR1\neq12\right) \)

• Sum-of-the-Years’-Digits Method
  

　\( Z=\displaystyle\frac{n\left(n+1\right)}{2} \)
　\( n^′=n-\displaystyle\frac{YR1}{12} \)
　\( Z^′=\displaystyle\frac{\left(Intg\left(n^′\right)+1\right)\left(Intg\left(n^′\right)+2\times{Frac\left(n^′\right)}\right)}{2} \)
　\( SYD_{1}=\displaystyle\frac{n}{Z}\times\displaystyle\frac{YR1}{12}\left(PV-FV\right) \)
　\( SYD_{j}=\left(\displaystyle\frac{n^′-j+2}{Z^′}\right)\left(PV-FV-SYD_{1}\right) \qquad \left(j\neq1\right) \)
　\( SYD_{n+1}=\left(\displaystyle\frac{n^′-\left(n+1\right)+2}{Z^′}\right)\left(PV-FV-SYD_{1}\right)\times\displaystyle\frac{12-YR1}{12} \qquad \left(YR1\neq12\right) \)
　\( RDV_{1} = PV-FV-SYD_{1} \)
　\( RDV_{j} = RDV_{j-1}-SYD_{j} \)

• Declining-Balance Method
  　\( DB_{1}=PV\times\displaystyle\frac{I\%}{100n}\times\displaystyle\frac{YR1}{12} \)
  　\( RDV_{1}=PV-FV-DB_{1} \)
  　\( DB_{j}=\left(RDV_{j-1}+FV\right)\times\displaystyle\frac{I\%}{100n} \)
  　\( RDV_{j}=RDV_{j-1}-DB_{j} \)
  　\( DB_{n+1}=RDV_{n} \qquad \left(YR1\neq12\right) \)
  　\( RDV_{n+1}=0 \qquad \qquad \left(YR1\neq12\right) \)

Bond Calculation

Bond Calculation lets you calculate the purchase price or the annual yield of a bond.

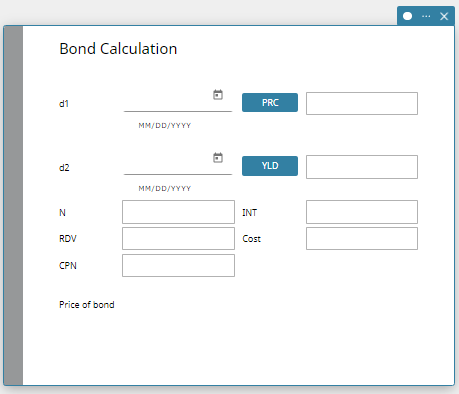
• Bond Calculation Fields
  The following fields appear on the Bond Calculation.

Field	Description
d1	Purchase date
d2	Redemption date
N	Number of periods
RDV	Redemption value
CPN	Annual coupon rate
PRC	Price of bond
YLD	Annual yield (as a percent)
INT	Interest accumulated during partial year portion of investment period
Cost	Cost of bond (price plus partial year interest)

Calculation Formulas

• Terms in the formulas
  
  　\(PRC\) ： price per $100 of face value
  　\(RDV\) ： redemption price per $100 of face value
  　\(CPN\) ： coupon rate (%)
  　\(YLD\) ： annual yield (%)
  　\(M\) ： number of coupon payments per year (1 = Annual, 2 = Semi-annual)
  　\(N\) ：number of coupon payments until maturity (n is used when “Term” is specified for “Bond Interval”.)
  　\(INT\) ： accrued interest
  　\(CST\) ： price including interest
  　\(A\) ： accrued days
  　\(D\) ： number of days in coupon period where settlement occurs
  　\(B\) ：number of days from purchase date until next coupon payment date (\(=D–A\))

• \(PRC\) when “Date” is specified for “Bond Interval”
  　For one or fewer coupon period to redemption:
  

　\( PRC=\displaystyle\frac{RDV+CPN/M}{1+\left(B/D\times\left(YLD/100\right)/M\right)}+A/D\times{CPN/M} \)
　For more than one coupon period to redemption:

　\( \displaystyle PRC=-\displaystyle\frac{RDV}{{\left(1+\left(YLD/100\right)/M\right)}^{ \left( N-1+B/D \right) }} \quad – \sum_{k=1}^N\displaystyle\frac{CPN/M}{{\left(1+\left(YLD/100\right)/M\right)}^{\left( N-1+B/D \right) }} \quad + A/D\times{CPN/M} \)
　\( INT=-A/D\times{CPN/M} \qquad CST=PRC\times{INT} \)

• \(PRC\) when “Term” is specified for “Bond Interval”
  

　\( \displaystyle PRC=-\displaystyle\frac{RDV}{{\left(1+\left(YLD/100\right)/M\right)}^{n}} \quad -\sum_{k=1}^n\displaystyle\frac{CPN/M}{{\left(1+\left(YLD/100\right)/M\right)}^{k}} \qquad INT=0 \qquad CST=PRC \)

• \(YLD\)
  　Annual yield (YLD) is calculated using Newton’s Method. As a consequence, the calculation results are numerical approximations whose precision can be affected by various calculation conditions. Interest calculation results produced by this application should be used keeping the above in mind, or results should be confirmed separately.

Break-Even Point

Break-Even Point lets you calculate the amount you must sell to break even or to obtain a specified profit, as well as the profit or loss on particular sales.

• Break-Even Point Fields
  The following fields appear on the Break-Even Point calculation.

Field	Description
PRC	Selling price per unit
VCU	Variable cost per unit
FC	Fixed costs
PRF	Amount of profit realized
QBE	Number of units to be sold
SBE	Amount that must be obtained from sales to break even
\(r\)%	Proportion of sales amount retained as a profit (as a percent)

Calculation Formulas

• Profit (Profit Amount/Ratio Setting: Amount (PRF))
  　\( QBE=\displaystyle\frac{FC+PRF}{PRC-VCU} \)
  　\( SBE=\displaystyle\frac{FC+PRF}{PRC-VCU}\times{PRC} \)
• Profit (Profit Amount/Ratio Setting: Ratio (r%))
  

　\( QBE=\displaystyle\frac{FC}{PRC\times\left(1-\displaystyle\frac{r\%}{100}\right)-VCU} \)
　\( SBE=\displaystyle\frac{FC}{PRC\times\left(1-\displaystyle\frac{r\%}{100}\right)-VCU}\times{PRC} \)

Margin of Safety

Margin of Safety lets you calculate how much sales can be reduced before losses are incurred.

• Margin of Safety Fields
  The following fields appear on the Margin of Safety calculation.

Field	Description
SAL	Amount obtained from sales
SBE	Break-even sales (amount that must be obtained from sales to break even)
MOS	Margin of safety (portion of sales amount above break-even point)

Calculation Formulas
\( MOS=\displaystyle\frac{SAL-SBE}{SAL} \)

Operating Leverage

Operating Leverage lets you calculate the degree of change in net earnings arising from a change in sales amount.

• Operating Leverage Fields
  The following fields appear on the Operating Leverage calculation.

Field	Description
SAL	Amount currently obtained from sales
VC	Variable cost for this level of production
FC	Fixed costs
DOL	Degree of operating leverage

Calculation Formulas
\( DOL=\displaystyle\frac{SAL-VC}{SAL-VC-FC} \)

Financial Leverage

Financial Leverage lets you calculate the degree of change in net earnings arising from a change in interest paid.

• Financial Leverage Fields
  The following fields appear on the Financial Leverage calculation.

Field	Description
EBIT	Earnings before interest and taxes
INT	Interest to be paid to bondholders
DFL	Degree of financial leverage

Calculation Formulas
\( DFL=\displaystyle\frac{EBIT}{EBIT-INT} \)

Combined Leverage

Combined Leverage lets you calculate the combined effects of operation and financial leverages.

• Combined Leverage Fields
  The following fields appear on the Combined Leverage calculation.

Field	Description
SAL	Amount obtained from sales
VC	Variable cost for this level of production
FC	Fixed costs
INT	Interest to be paid to bondholders
DCL	Degree of combined leverage

Calculation Formulas
\( DCL=\displaystyle\frac{SAL-VC}{SAL-VC-FC-INT} \)

Quantity Conversion

Quantity conversion enables the calculations below.

• Quantity Conversion lets you calculate the number of items sold, selling price, or sales amount given the other two values.

• It also lets you calculate the number of items manufactured, unit variable cost, or total variable cost given the other two values.
  

• Quantity Conversion Fields
  The following fields appear on the Combined Leverage calculation.

Field	Description
SAL	Amount obtained from sales
PRC	Selling price per unit
QTY	Number of units sold
VC	Variable cost for this level of production
VCU	Variable cost per unit
QTY	Number of units manufactured

Calculation Formulas
\(SAL=PRC\times{QTY}\)
\(VC=VCU\times{QTY}\)