Statistical Calculations

table of contents

Basic Statistical Calculation Operations
Editing Statistical Data Values
Selecting Data Values for Statistical Calculation
Performing One-variable Statistical Calculations
Drawing a Regression Graph
Drawing a Histogram
Drawing a Box-and-whisker Diagram
Drawing a Circle Graph
Scatter Plot Operations
Performing a One-Sample Z-Test
Statistical Calculations and Graphs

Basic Statistical Calculation Operations

• To enter values into a Statistical Data sticky note
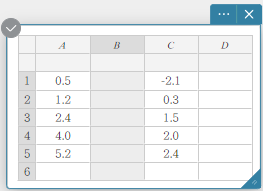
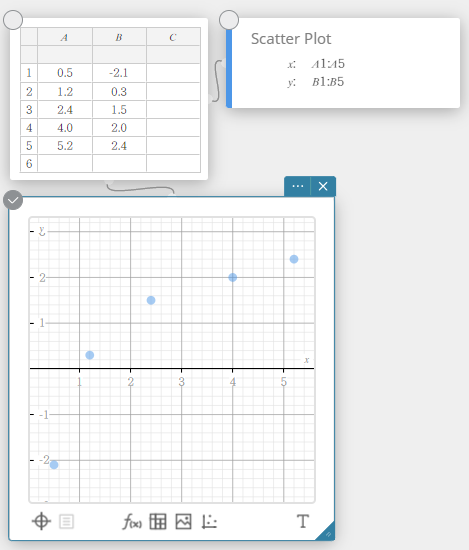
  In the example shown in this section, the data values in the table below are entered into cells A1 through B5 of a Statistical Data sticky note.

	A	B
1	\(0.5\)	\(-2.1\)
2	\(1.2\)	\(0.3\)
3	\(2.4\)	\(1.5\)
4	\(4.0\)	\(2.0\)
5	\(5.2\)	\(2.4\)

1. Click in the sticky note menu.
   
   This displays a Statistical Data sticky note.
   
   Cell A1 becomes selected for input at this time.
2. Enter \(0.5\) into cell A1 and then press [Enter].
   Cell A2 becomes selected for input.
3. Enter \(1.2\) into cell A2 and then press [Enter].
   Cell A3 becomes selected for input. Similarly, enter data up to cell A5.
4. Click cell B1.
   Cell B1 becomes selected for input.
5. Enter \(-2.1\) into cell B1 and then press [Enter].
   Cell B2 becomes selected for input. Column C is also created at this point (see MEMO below).
6. Enter \(0.3\) into cell B2 and then press [Enter].
   Cell B3 becomes selected for input. Similarly, enter data up to cell B5.　　
   
   MEMO
   Entering a value into the rightmost column automatically adds a new column to the right of it.
   
   The cells under the column labels (A, B, C,…) can be used to enter a list name for each column. For details, see “Assigning a Name to a List”.

• Selecting Data Values for Statistical Calculation

1. Use the procedure under “Entering Values into a Statistical Data Sticky Note” to enter data values.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)

2. Use your computer mouse to drag from cell A1 to cell B5.
   This selects the range of cells from cell A1 through cell B5.
   
   MEMO
   You can select an entire column by clicking its column number.
   You can select an entire row by clicking its row number.
   You can click or drag across column numbers and use the data in those columns to draw a graph.
   In this case, after drawing the graph, you can also use the drop-down list of the Graph sticky note to select other column numbers and redraw the graph.
   

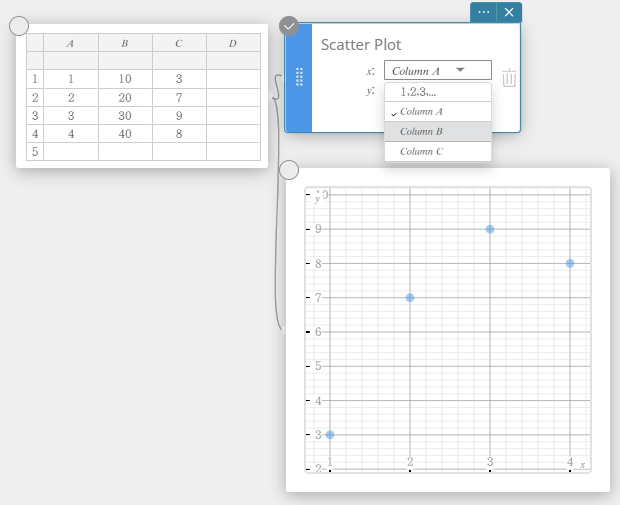
• Performing Statistical Calculations

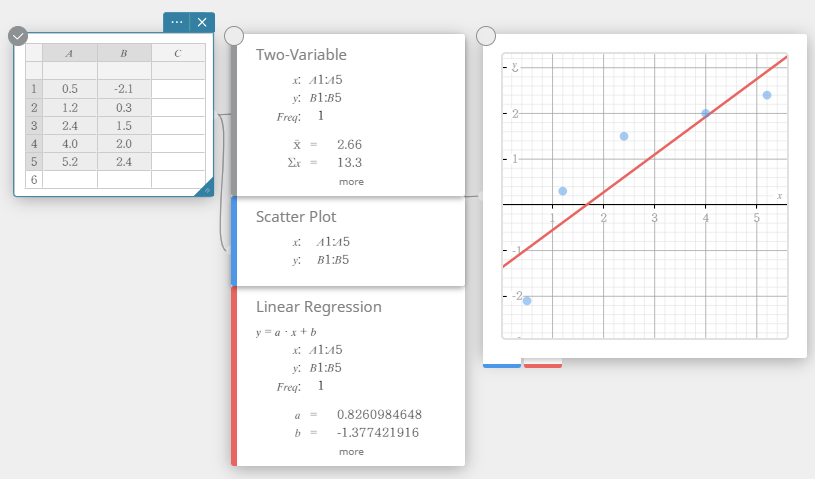
In this example, we perform two-variable statistical calculations and draw a scatter plot and a linear regression graph.

1. Enter the data values in the table below, and then select all of the data.
   

   	A	B
   1	\(0.5\)	\(-2.1\)
   2	\(1.2\)	\(0.3\)
   3	\(2.4\)	\(1.5\)
   4	\(4.0\)	\(2.0\)
   5	\(5.2\)	\(2.4\)

   

2. On the software keyboard, click [Calculation] – [Two-Variable].
   
   This displays two-variable statistical calculation results.
   
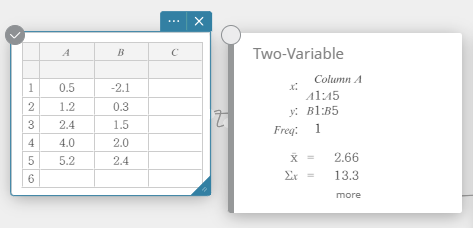
3. Click on the software keyboard.
   
4. On the software keyboard, click [Graph] – [Scatter Plot].
   
   This creates a Scatter Plot sticky note and simultaneously draws a scatter plot on the Graph sticky note.
   
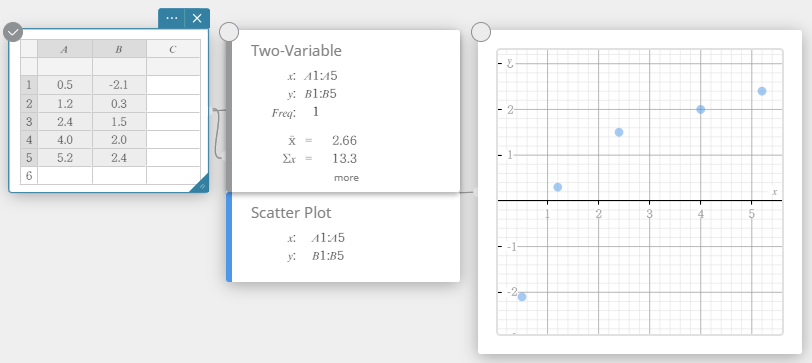
5. Click on the software keyboard.
6. On the software keyboard, click [Regression] – [Linear Regression].
   
   This creates a Linear Regression sticky note and simultaneously draws a linear regression graph on the Graph sticky note.
   

• To draw a statistical graph by using a template.
  With a template, you can draw a statistical graph easily.
  The example here shows how to draw a graph of the normal probability distribution calculation.

1. Click in the sticky note menu.
   
   This displays a Statistics sticky note.
2. Select [Distribution].
   
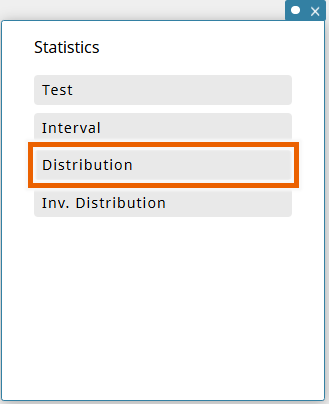
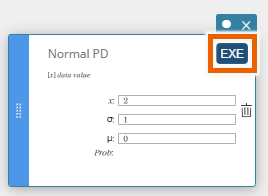
3. Select [Normal PD].
   
   This displays a Normal PD template.
4. Enter values and select [EXE] or press [Enter] key.
   
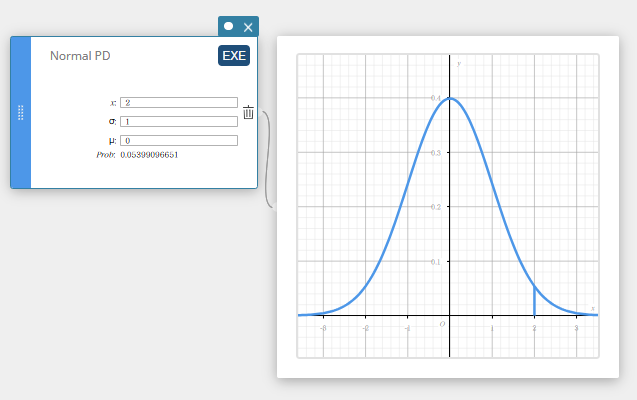
   This draws the graph.
   

Editing Statistical Data Values

• To correct data values

1. Click on the cell that contains the data value you want to correct.
   
2. Enter the new data value and then press [Enter].
   

• To insert a row

1. Right-click the number of the row where you want to insert a new row.
   This displays a menu.
   
2. Click [Insert].
   This inserts a row.
   

• To insert a column

1. Right-click the header of the column where you want to insert a new column.
   This displays a menu.
   
2. Click [Insert].
   This inserts a column.
   

• To delete a row

1. Right-click the number of the row you want to delete.
   This displays a menu.
   
2. Click [Delete].
   This deletes the row.
   

• To delete a column

1. Right-click the header of the column you want to delete.
   This displays a menu.
   
2. Click [Delete].
   This deletes the column.
   

• Assigning a Name to a List

Once you assign a name to a list, you can use the name in tests and other statistical calculations. List names are entered into the cells below the column names.

Example: To assign the name “List1” to column A

1. Double-click the cell under A.
   This selects the cell for list name input.
   
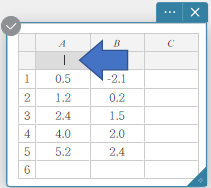
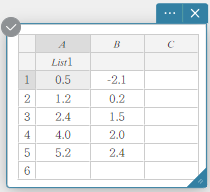
2. Enter the list name “List1” and then press [Enter].
   This assigns “List1” as the list name of column A.
   
   MEMO
   The following rules apply to list names.
   － List names can be up to 8 bytes long.
   － The following characters are allowed in a list name: Upper-case and lower-case characters, subscript characters, numbers.
   － List names are case-sensitive. For example, each of the following is treated as a different list name: abc, Abc, aBc, ABC.

Selecting Data Values for Statistical Calculation

You can select a range of cells by dragging the mouse pointer across them.

Data Selection Examples

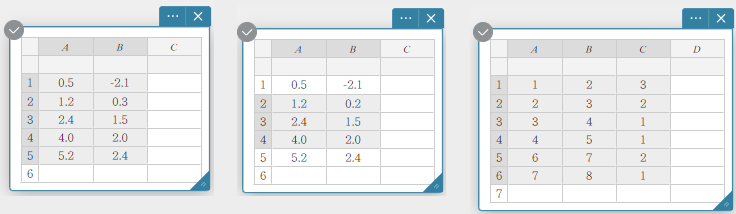
MEMO
You can select an entire column by clicking its column number.
You can select an entire row by clicking its row number.

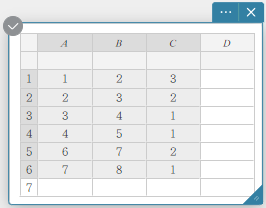
Statistical calculations can be performed if the range of selected cells includes one or more blank cells.
Up to three columns can be used for statistical calculations. Statistical calculations cannot be performed if more than three columns are selected.

Performing One-variable Statistical Calculations

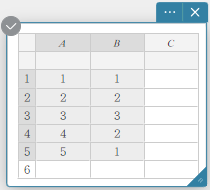
1. Enter the data values in the table below, with data in column A and frequency in column B.
   

   Data	Frequency
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Drag from cell A1 to cell B5 to select the range of cells between them.
   

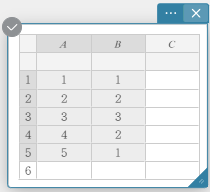
3. On the software keyboard, click [Calculation] – [One-Variable].
   This displays one-variable statistical calculation results.
   
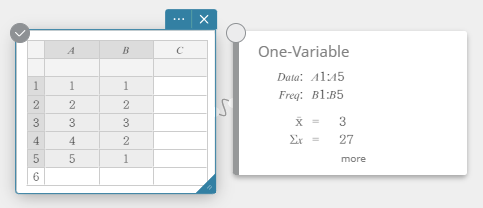
4. To display other hidden calculation result items, click [more] on the Statistical Calculation sticky note.
   This displays the hidden calculation results.
   To return the Statistical Calculation sticky note to its reduced size configuration, click [hide].
   

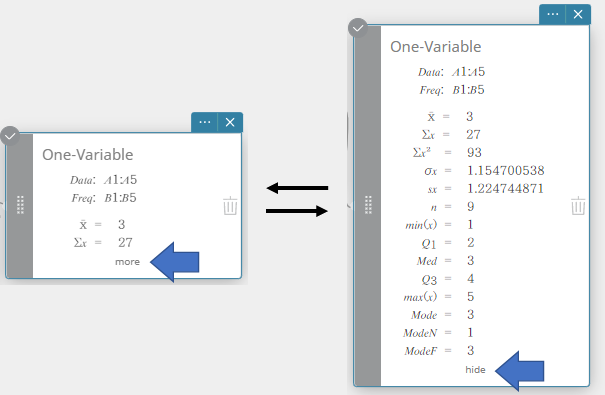
Performing a one-variable statistical calculation displays the results below.
\(\bar{\rm x}\)　　　sample mean
\(\Sigma {\rm x}\)　　 sum of data
\(\Sigma {\rm x}^2\)　　 sum of squares
\(\sigma {\rm x}\)　　　population standard deviation
\({\rm sx}\)　　　 sample standard deviation
\({\rm n}\)　　　　sample size
\({\rm min(x)}\)　minimum
\({\rm Q}_1\)　　　first quartile
\({\rm Med}\)　　 median
\({\rm Q}_3\)　　　 third quartile
\({\rm max(x)}\)　maximum
\({\rm Mode}\)　　mode
\({\rm ModeN}\)　 number of data mode items
\({\rm ModeF}\)　data mode frequency
When \({\rm Mode}\) has multiple solutions, they are all displayed.

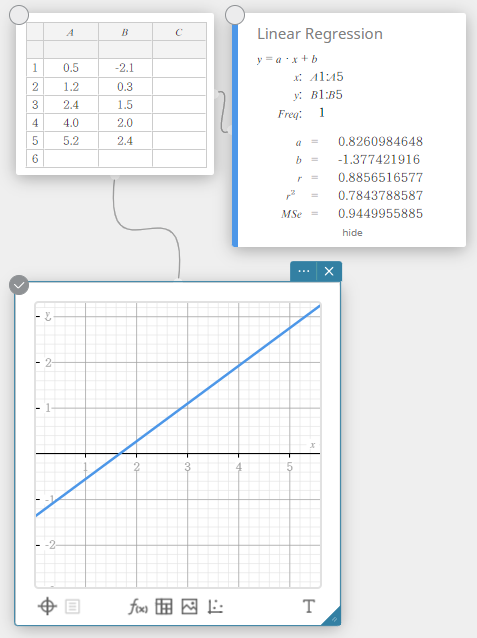
Drawing a Regression Graph

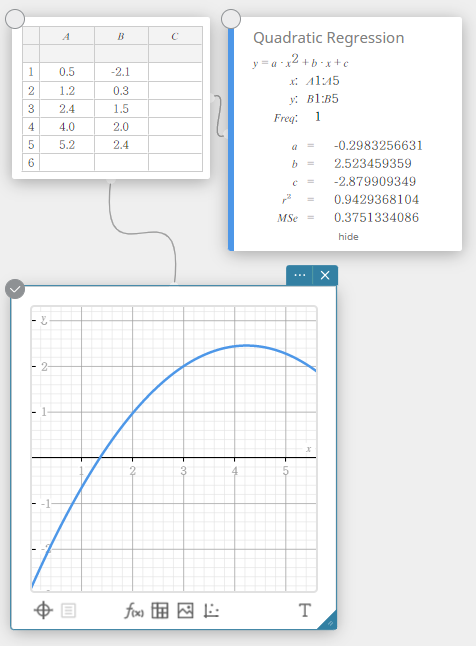
In this example, we will use the data values below to draw a scatter plot, linear regression graph, and a quadratic regression graph.

1. Enter the data values in the table below, and then select all of the data.
   

   A	B
   \(1.0\)	\(1.0\)
   \(1.2\)	\(1.1\)
   \(1.5\)	\(1.2\)
   \(1.6\)	\(1.3\)
   \(1.9\)	\(1.4\)
   \(2.1\)	\(1.5\)
   \(2.4\)	\(1.6\)
   \(2.5\)	\(1.7\)
   \(2.7\)	\(1.8\)
   \(3.0\)	\(2.0\)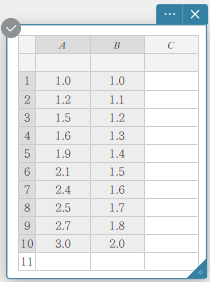

   

2. On the software keyboard, click [Graph] – [Scatter Plot].
   
   This creates a Scatter Plot sticky note and simultaneously draws a scatter plot on the Graph sticky note.
   
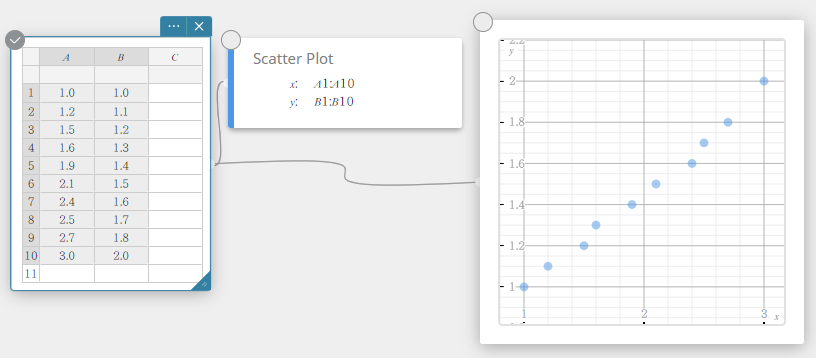
3. Click on the software keyboard.
   
4. On the software keyboard, click [Regression] – [Linear Regression].
   
   This creates a Linear Regression sticky note and simultaneously draws a linear regression graph on the Graph sticky note.
   
5. On the software keyboard, click [Quadratic Regression].
   
   This creates a Quadratic Regression sticky note and simultaneously draws a quadratic regression graph on the Graph sticky note.
   

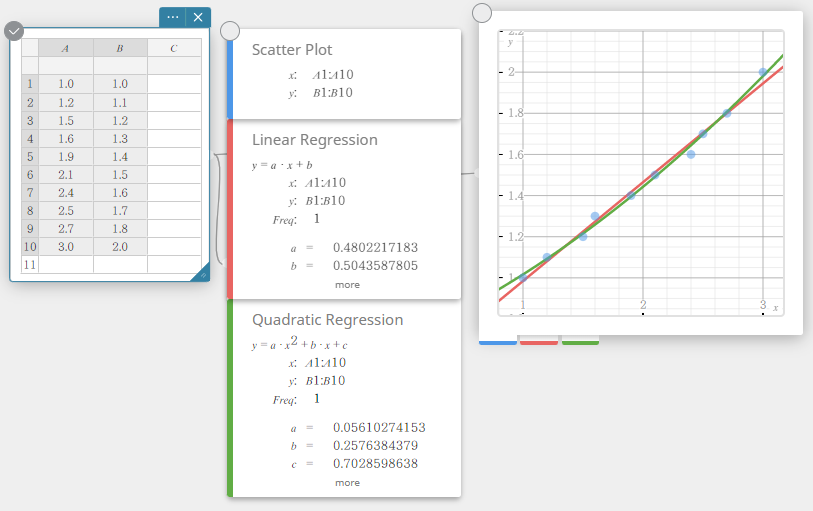
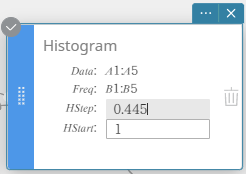
Drawing a Histogram

1. Enter the data values in the table below, with data in column A and frequency in column B.
   

   Data	Frequency
   \(1\)	\(1\)
   \(2\)	\(2\)
   \(3\)	\(3\)
   \(4\)	\(2\)
   \(5\)	\(1\)

2. Drag from cell A1 to cell B5 to select the range of cells between them.
   

3. On the software keyboard, click [Graph] – [Histogram].
   This creates a Histogram sticky note and simultaneously draws a histogram on the Graph sticky note.
   
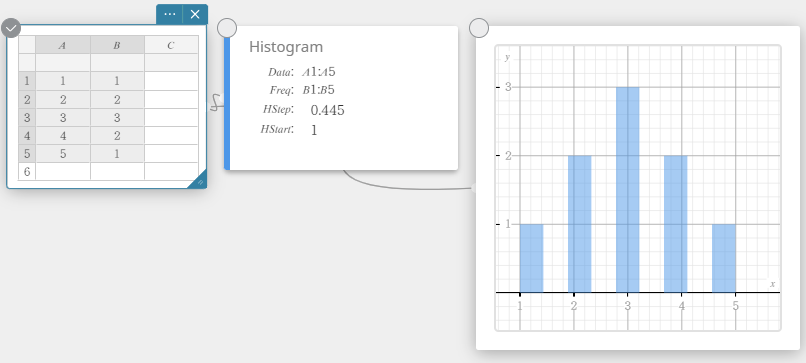
   MEMO
   You can change the histogram draw start value (HStart) and step value (HStep). On the Histogram sticky note, click HStart or HStep and then enter the value you want.
   

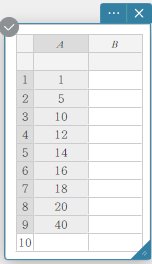
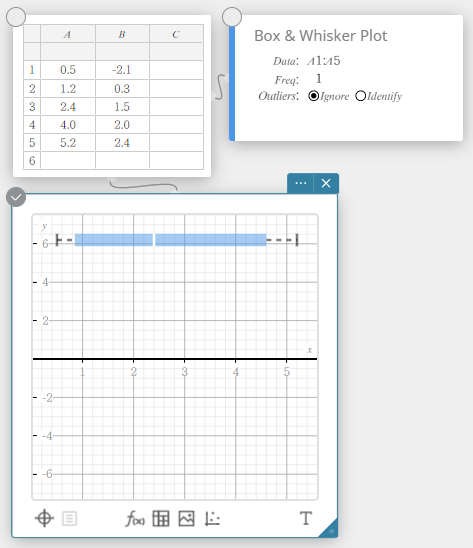
Drawing a Box-and-whisker Diagram

1. Enter the data values in the table below in column A.
   

   A
   \(1\)
   \(5\)
   \(10\)
   \(12\)
   \(14\)
   \(16\)
   \(18\)
   \(20\)
   \(40\)

2. Drag from cell A1 to cell A9 to select the range of cells between them.
   

3. On the software keyboard, click [Graph] – [Box & Whisker Plot].
   This creates a Box & Whisker Plot sticky note and simultaneously draws a box-and-whisker diagram on the Graph sticky note.
   
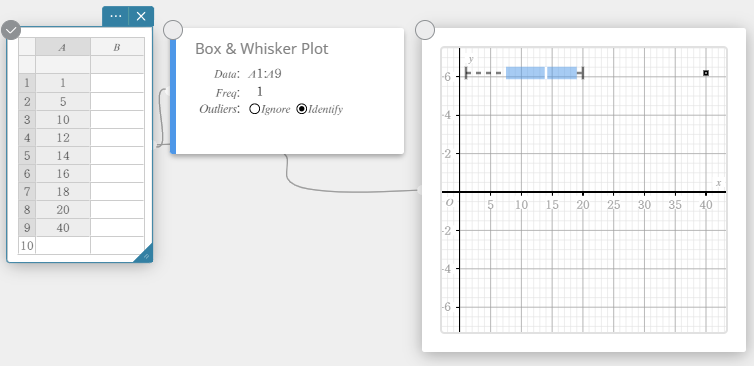
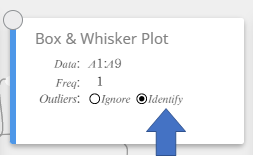
   MEMO
   You can display outlier values. To do so, select [Identify] for the Outliers item of the Box & Whisker Plot sticky note.
   

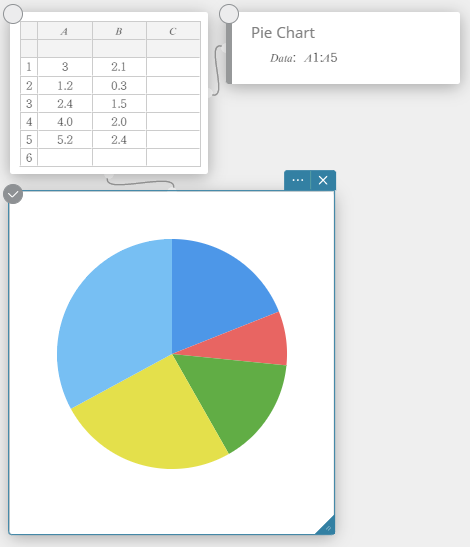
Drawing a Circle Graph

1. Enter the data values in the table below in column A.
   

   A
   \(5\)
   \(10\)
   \(20\)
   \(30\)
   \(40\)

2. Drag from cell A1 to cell A5 to select the range of cells between them.
   

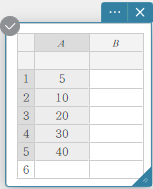
3. On the software keyboard, click [Graph] – [Pie Chart].
   This creates a Pie Chart sticky note and simultaneously draws a pie graph on a separate sticky note*.
   
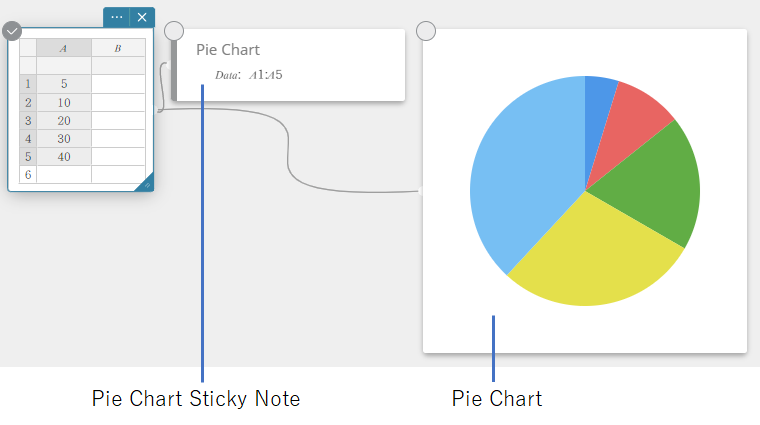
   *　This draws the graph on the Graph sticky note. The type is different when a circle graph is drawn on the sticky note.

Scatter Plot Operations

• To move the points of a scatter plot

1. Enter the data values in the table below in columns A and B.
   

   Data	Frequency
   \(0.5\)	\(-2.1\)
   \(1.2\)	\(0.3\)
   \(2.4\)	\(1.5\)
   \(4.0\)	\(2.0\)
   \(5.2\)	\(2.4\)

2. Drag from cell A1 to cell B5 to select the range of cells between them.
   

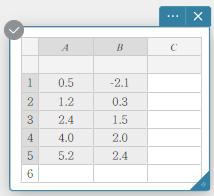
3. On the software keyboard, click [Graph] – [Scatter Plot].
   This creates a Scatter Plot sticky note and Graph sticky note, and draws a scatter plot on the Graph sticky note.
   
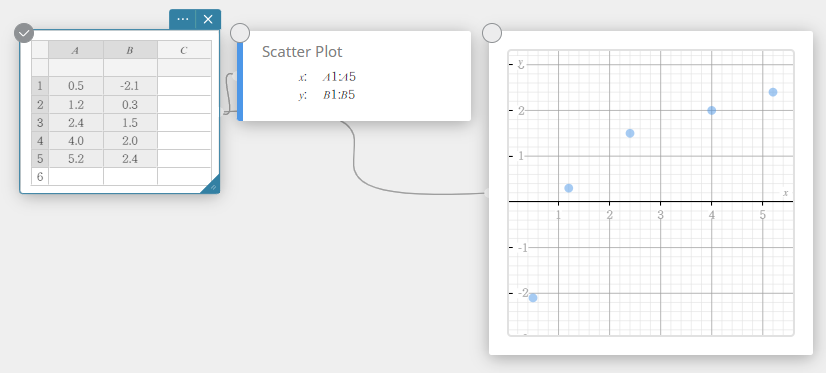
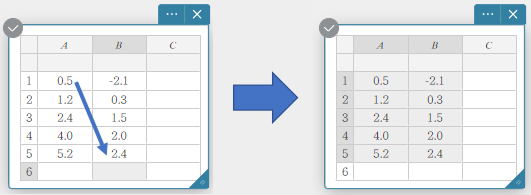
4. To move a scatter plot point, drag it.
   This will also change the Statistical Data sticky note values to the coordinates of the destination.
   

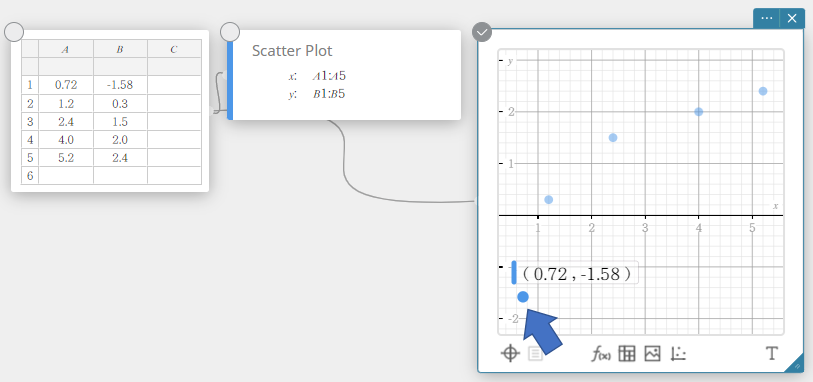
• To lock a cell

MEMO
When a cell is locked, its data value will not change even if you try to move its scatter plot point. For example, if you lock a column A cell, the corresponding scatter plot point cannot be moved along the x-axis.

1. Continuing from the procedure under “To move the points of a scatter plot”, select cell A1.
2. Click on the Statistical Calculation sticky note.
   
3. Click the icon beside [Lock].
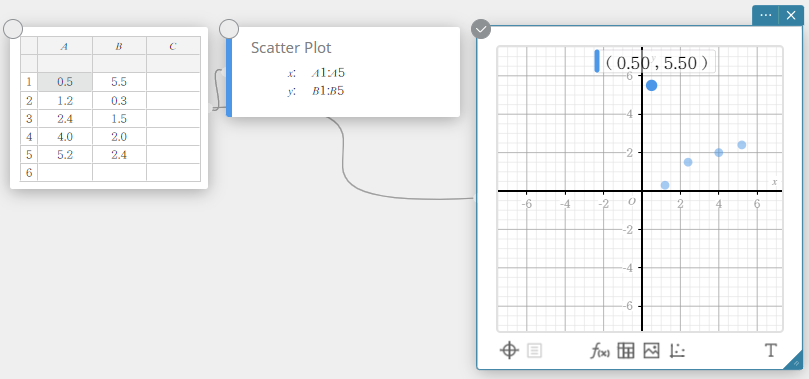
   This locks cells A1. If you drag the scatter plot point that corresponds to cells A1 and B1, movement will not be possible along the x-axis.
   

• To unlock a cell

1. Select the locked cell that you want to unlock.
2. Click on the Statistical Calculation sticky note.
   
3. Click the icon beside [Unlock].

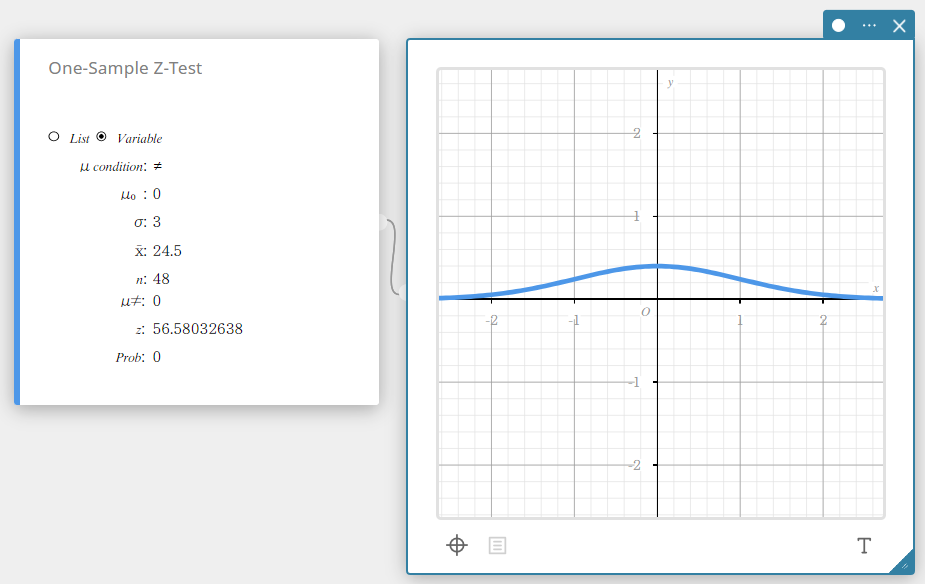
Performing a One-Sample Z-Test

• To specify the number of data samples and then perform a one-sample Z-test

Example:
Sample size: \(n=48\)
Sample mean: \(\overline{x}=24.5\)
Null hypothesis: \(\mu \ne 0\)
Standard deviation: \(\sigma=3\)

1. Create a Statistical Data sticky note.
2. On the software keyboard, click [Test] – [One-Sample Z-Test].
   
   This creates a One-Sample Z-Test sticky note.
   
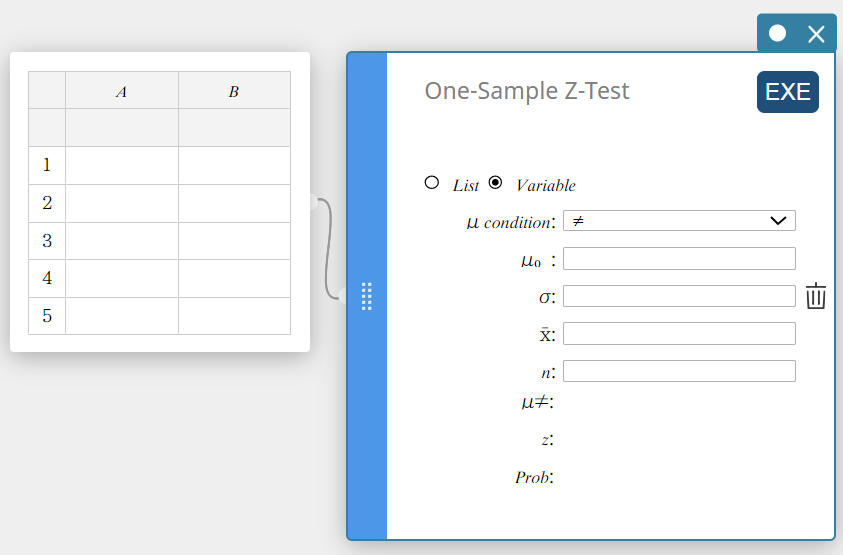
3. Configure settings as shown below.
   \(\mu\) condition: On the menu that appears, select “\(\ne\)”.
   \(\mu_0\) : Input \(0\).
   \(\sigma\): Input \(3\).
   \(\overline{x}\) : Input \(24.5\).
   \(n\) : Input \(48\).
   
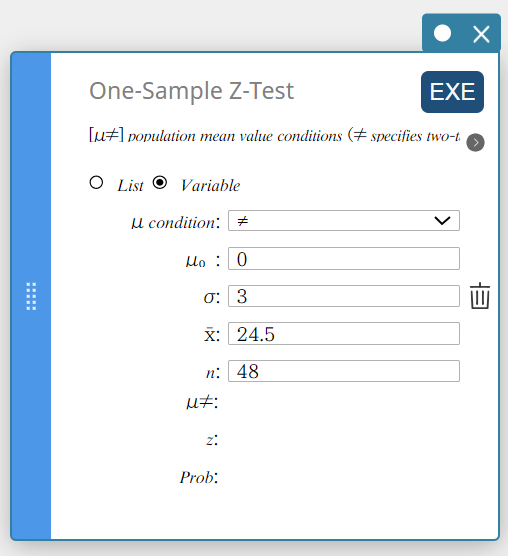
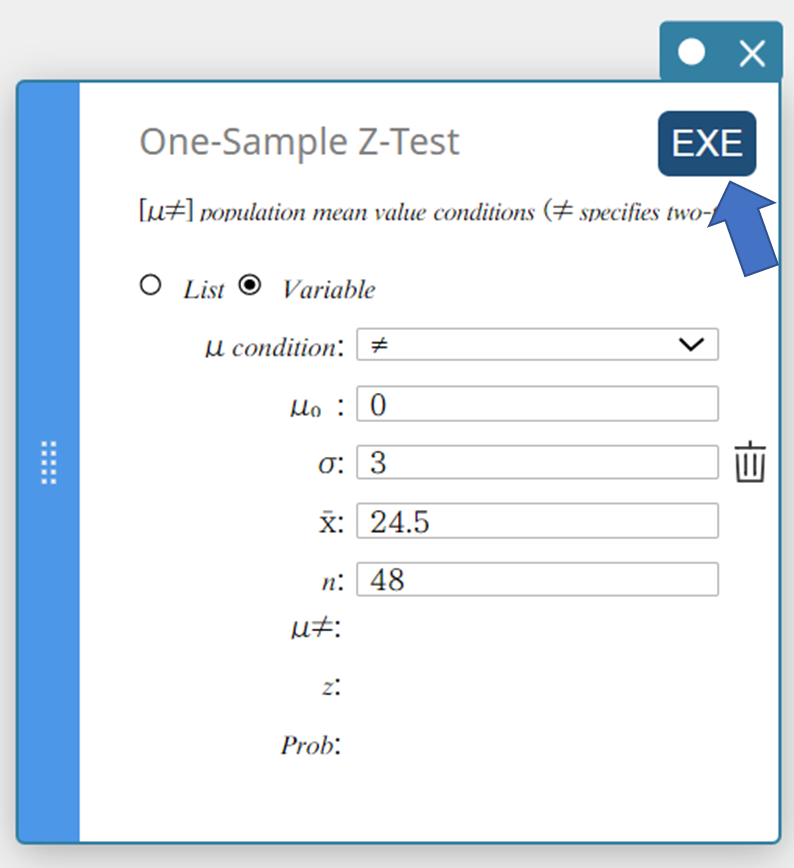
4. Click [EXE].
   
   This displays the calculation results and the graph.
   
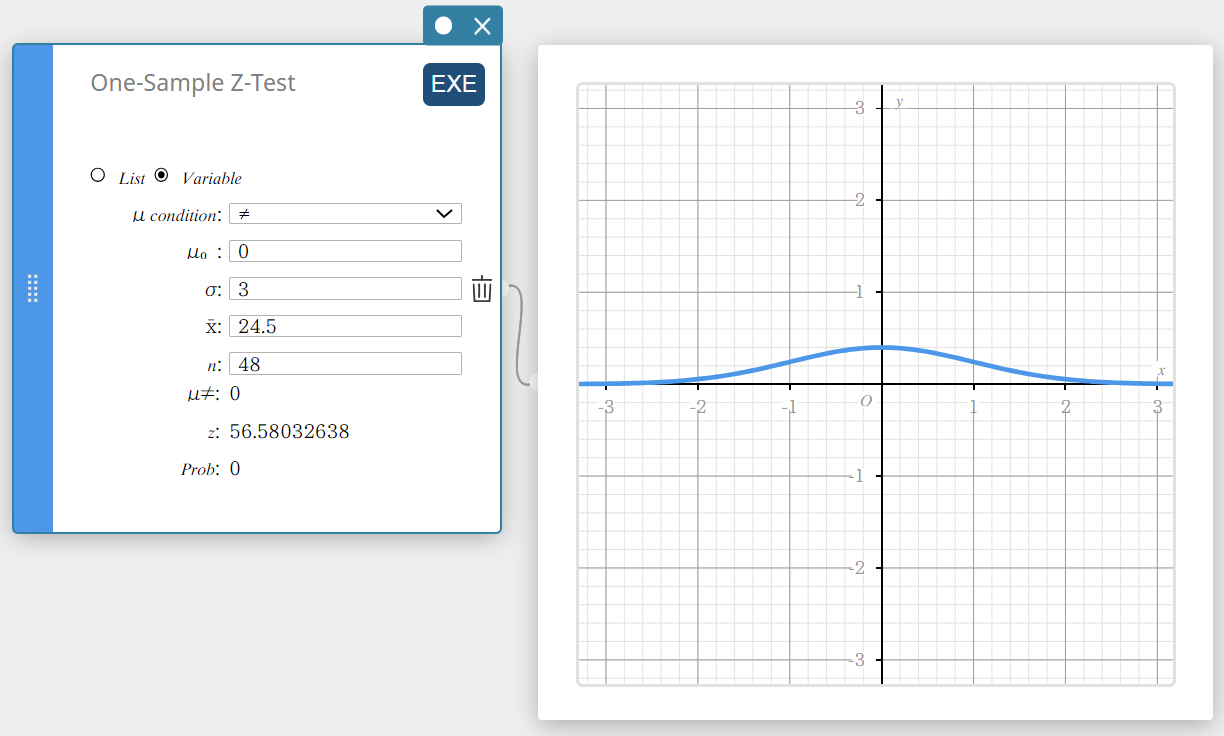
   \(\mu \ne\) population mean value condition
   \(\rm z\) 　　\(\rm z\) value
   Prob 　\(\rm p\) value
   \(\overline{x}\) 　　sample mean
   \(n\) 　　sample size

• To use lists to perform a one-sample Z-test

1. Input the following list names: List 1 for column A, List 2 for column B.
2. Input the data value in the table below.
   
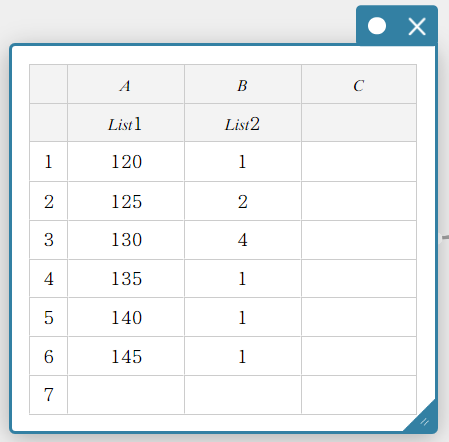
3. Drag from cell A1 to cell B6 to select the range of cells.
4. On the software keyboard, click [Test] – [One-Sample Z-Test].
   
   This creates a One-Sample Z-Test sticky note.
   
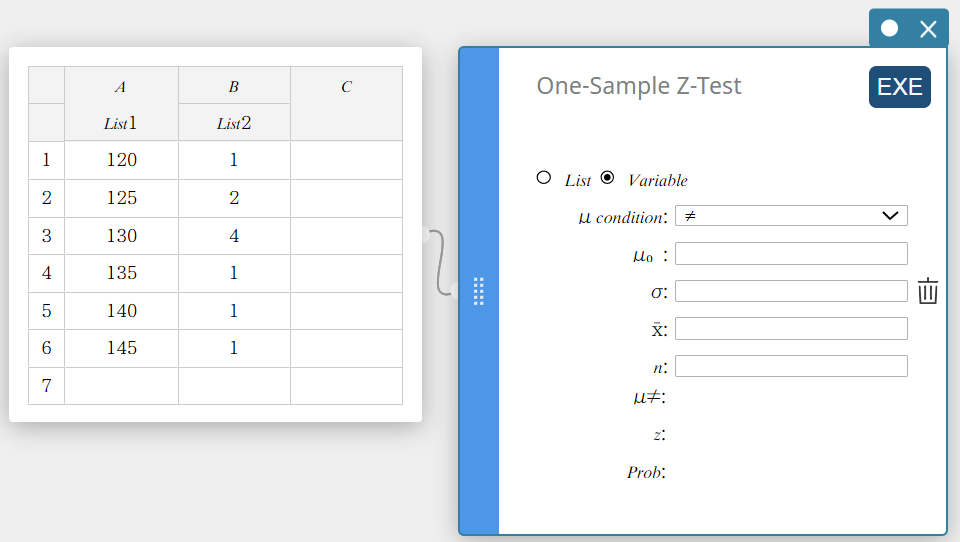
5. Click “List”.
   
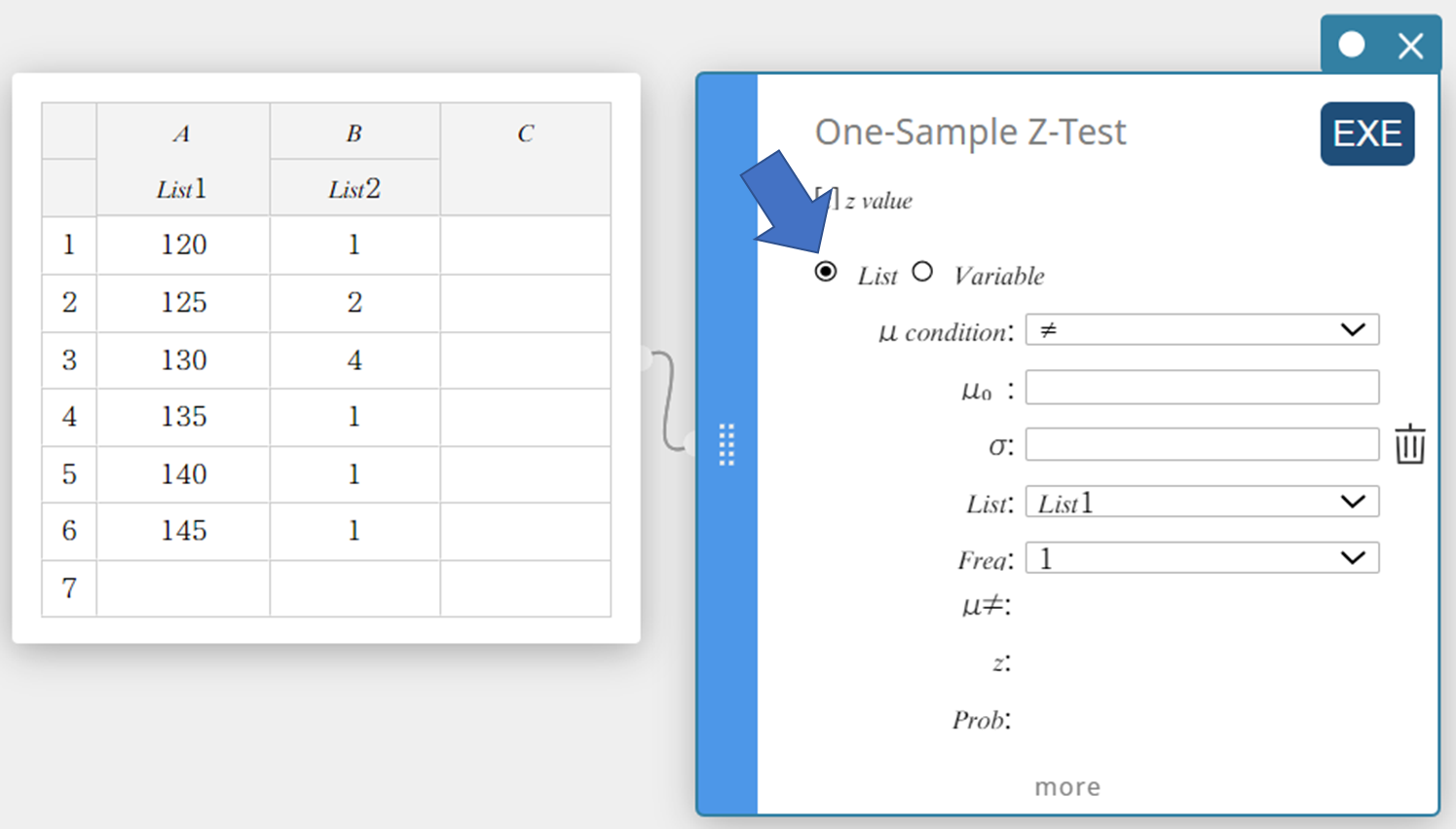
6. Configure settings as shown below.
   \(\mu\) condition: On the menu that appears, select “\(\gt\)”.
   \(\mu_0\) : Input \(120\).
   \(\sigma\): Input \(19\).
   List: On the menu that appears, select “List1”.
   Frequency: On the menu that appears, select “List2”.
   
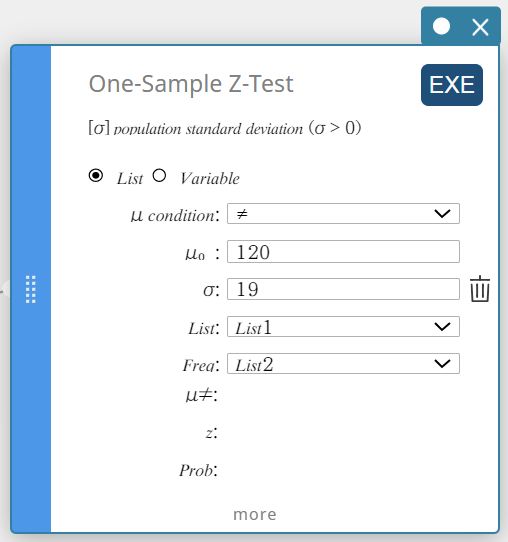
7. Click [EXE].
   
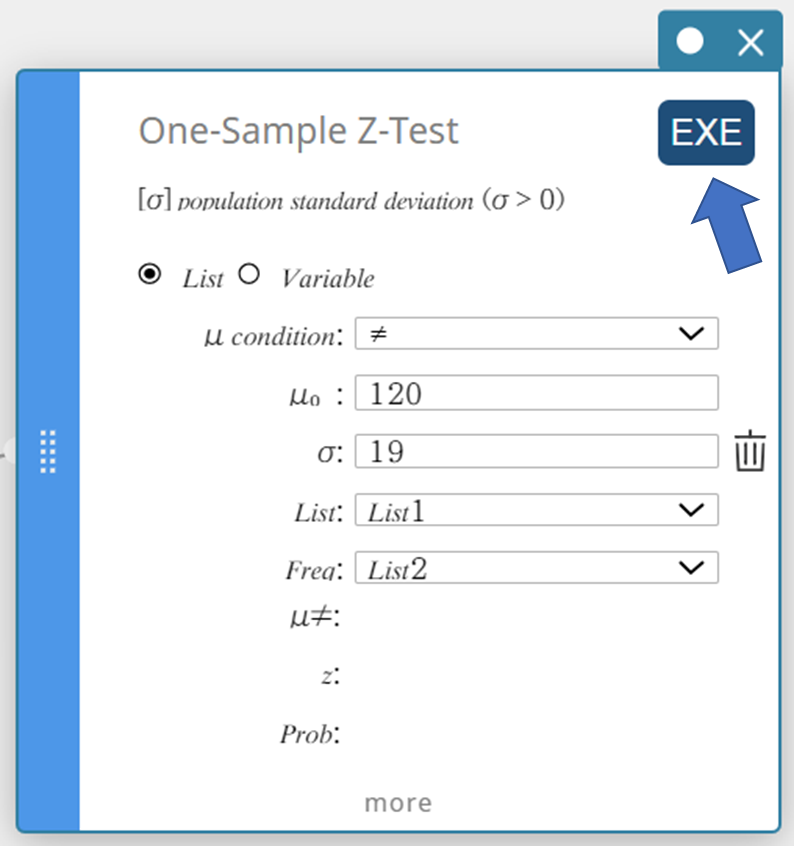
   This displays the calculation results and the graph.
   
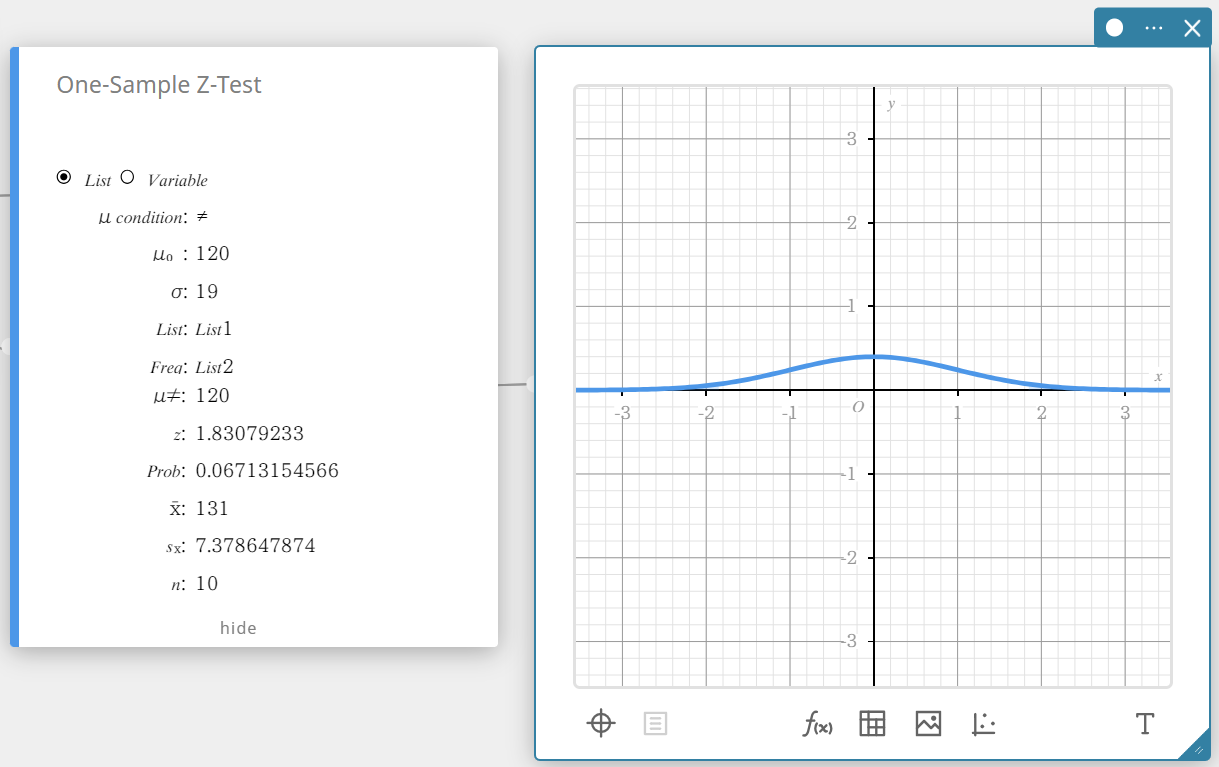
   \(\mu \gt\)　population mean value condition
   \(\rm z\)　　　\(\rm z\) value
   Prob　　\(\rm p\) value
   \(\overline{x}\)　　　sample mean
   \({\rm Sx}\)　　sample standard deviation
   \(n\)　　　sample size

Statistical Calculations and Graphs

Statistical Calculations

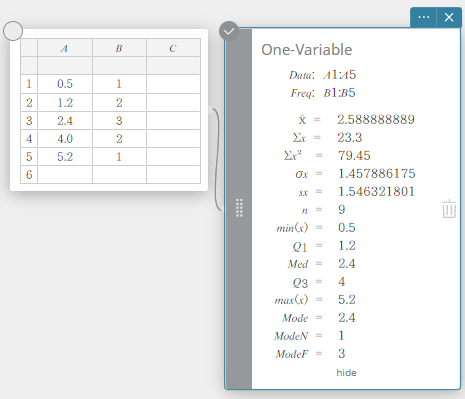
One-Variable
This displays the calculation results of one-variable statistics.

\(\bar{\rm x}\) … sample mean
\(\Sigma {\rm x}\) … sum of data
\(\Sigma {\rm x}^2\) … sum of squares
\(\sigma {\rm x}\) … population standard deviation
\({\rm sx}\) … sample standard deviation
\({\rm n}\) … sample size
\({\rm min(x)}\) … minimum
\({\rm Q}_1\) … first quartile
\({\rm Med}\) … median
\({\rm Q}_3\) … third quartile
\({\rm max(x)}\) … maximum
\({\rm Mode}\) … mode
\({\rm ModeN}\) … number of data mode items
\({\rm ModeF}\) … data mode frequency

When \({\rm Mode}\) has multiple solutions, they are all displayed.

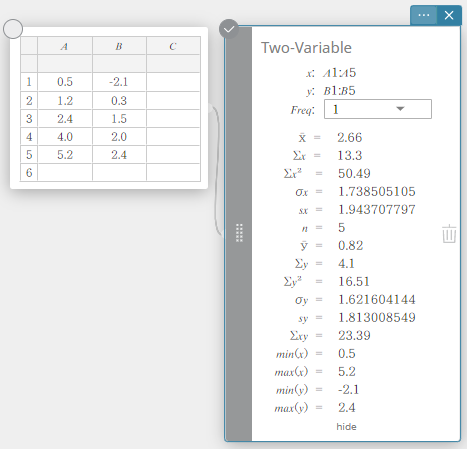
Two-Variable
This displays the calculation results of paired-variable statistics.

\(\bar{\rm x}\) … sample mean
\(\Sigma {\rm x}\) … sum of data
\(\Sigma {\rm x}^2\) … sum of squares
\(\sigma {\rm x}\) … population standard deviation
\({\rm sx}\) … sample standard deviation
\({\rm n}\) … sample size
\(\bar{\rm y}\) … sample mean
\(\Sigma {\rm y}\) … sum of data
\(\Sigma {\rm y}^2\) … sum of squares
\(\sigma {\rm y}\) … population standard deviation
\({\rm sy}\) … sample standard deviation
\(\Sigma {\rm xy}\) … sum of the products XList and YList data
\({\rm minX}\) … minimum
\({\rm maxX}\) … maximum
\({\rm minY}\)… minimum
\({\rm maxY}\) … maximum

Regression Calculations and Graphs

Linear Regression
Linear regression uses the method of least squares to determine the equation that best fits your data points, and returns values for the slope and y-intercept. The graphic representation of this relationship is a linear regression graph.

\(y = a \cdot x + b\)
\(a\) … regression coefficient (slope)
\(b\) … regression constant term (y-intercept)
\(r\) … correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

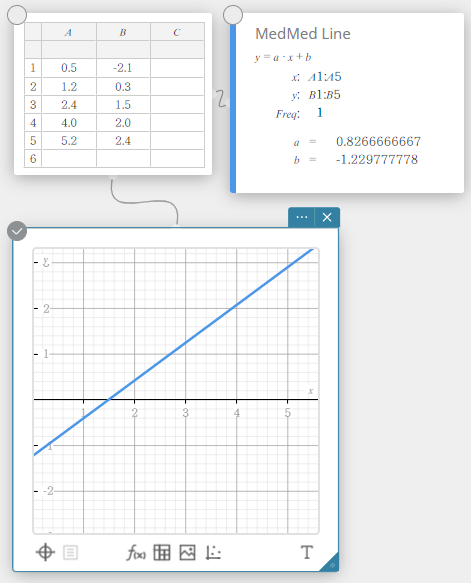
Med-Med Regression
When you suspect that the data contains extreme values, you should use the Med-Med graph (which is based on medians) in place of the linear regression graph. The Med-Med graph is similar to the linear regression graph, but it also minimizes the effects of extreme values.

\(y = a \cdot x + b\)
\(a\) … regression coefficient (slope)
\(b\) … regression constant term (y-intercept)

Quadratic Regression
Quadratic regression graph uses the method of least squares to draw a curve that passes the vicinity of as many data points as possible. This graph can be expressed as a quadratic regression expression.

\(y = a \cdot x^2 + b \cdot x + c\)
\(a\) … regression second coefficient
\(b\) … regression first coefficient
\(c\) … regression constant term (y-intercept)
\(r^2\) … coefficient of determination
\({\rm MSe}\) … coefficient of determination

Cubic Regression
Cubic regression graph uses the method of least squares to draw a curve that passes the vicinity of as many data points as possible. This graph can be expressed as a cubic regression expression.

\(y = a \cdot x^3 + b \cdot x^2 + c \cdot x + d\)
\(a\) … regression third coefficient
\(b\) … regression second coefficient
\(c\) … regression first coefficient
\(d\) … regression constant term (y-intercept)
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

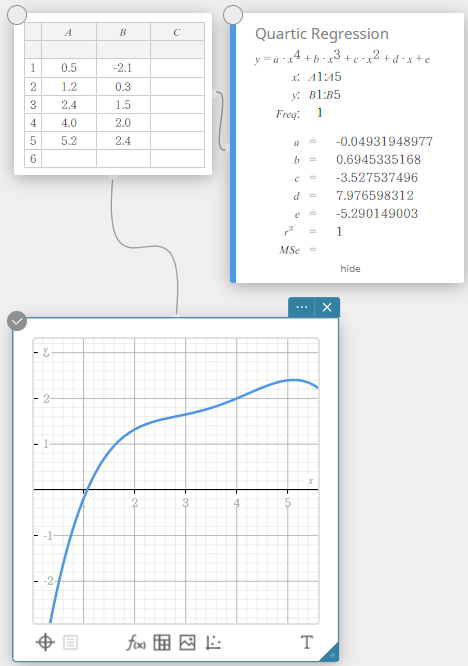
Quartic Regression
Quartic regression graph uses the method of least squares to draw a curve that passes the vicinity of as many data points as possible. This graph can be expressed as a quartic regression expression.

\(y = a \cdot x^4 + b \cdot x^3 + c \cdot x^2 + d \cdot x + e\)
\(a\) … regression fourth coefficient
\(b\) … regression third coefficient
\(c\) … regression second coefficient
\(d\) … regression first coefficient
\(e\) … regression constant term (y-intercept)
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

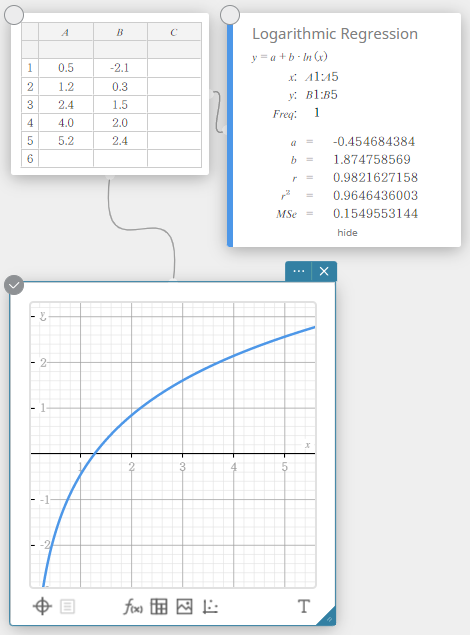
Logarithmic Regression
Logarithmic regression expresses \(y\) as a logarithmic function of \(x\). The normal logarithmic regression formula is \(y=a+b \cdot \ln(x)\). If we say that \(X=\ln(x)\), then this formula corresponds to the linear regression formula \(y=a+b \cdot X\).

\(y = a + b \cdot \ln(x)\)
\(a\) … regression constant term
\(b\) … regression coefficient
\(r\) … correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

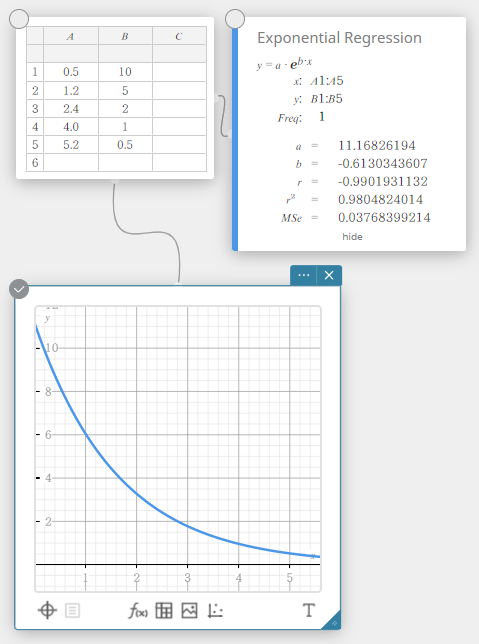
Exponential Regression
Exponential regression can be used when \(y\) is proportional to the exponential function of \(x\). The normal exponential regression formula is \(y=a \cdot e^{b \cdot x}\). If we obtain the logarithms of both sides, we get \(\ln(y)=\ln(a)+b \cdot x\). Next, if we say that \(Y=\ln(y)\) and \(A=\ln(a)\), the formula corresponds to the linear regression formula \(Y=A+b \cdot x\).

\(y = a \cdot e^{b \cdot x}\)
\(a\) … regression coefficient
\(b\) … regression constant term
\(r\) … correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

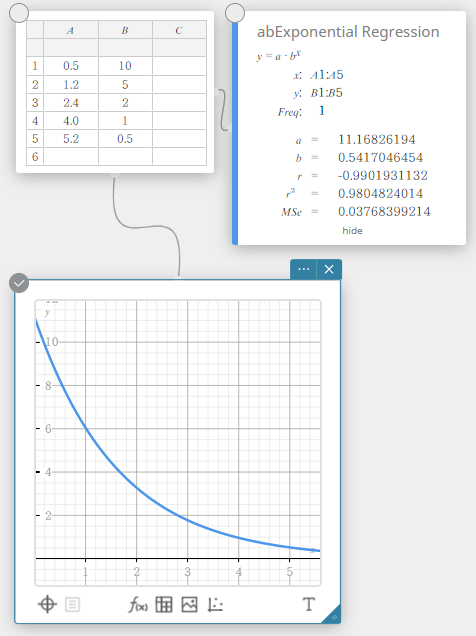
abExponential Regression
Exponential regression can be used when \(y\) is proportional to the exponential function of \(x\). The normal exponential regression formula in this case is \(y=a \cdot b^x\). If we take the natural logarithms of both sides, we get \(\ln(y)=\ln(a)+(\ln(b)) \cdot x\). Next, if we say that \(Y=\ln(y)\), \(A=\ln(a)\) and \(B=\ln(b)\), the formula corresponds to the linear regression formula \(Y=A+B \cdot x\).

\(y = a \cdot b^x\)
\(a\) … regression constant term
\(b\) … regression coefficient
\(r\) … correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

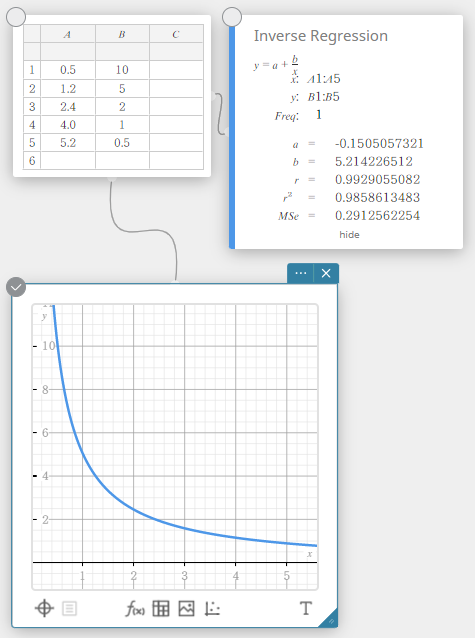
Inverse Regression
Inverse regression expresses \(y\) as an inverse function of \(x\). The normal inverse regression formula is \(y=a+b/x\). If we say that \(X=1/x\), then this formula corresponds to the linear regression formula \(y=a+b･X\).

\(y=a+b/x\)
\(a\) … regression constant term
\(b\) … regression coefficient
\(r\) …. correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

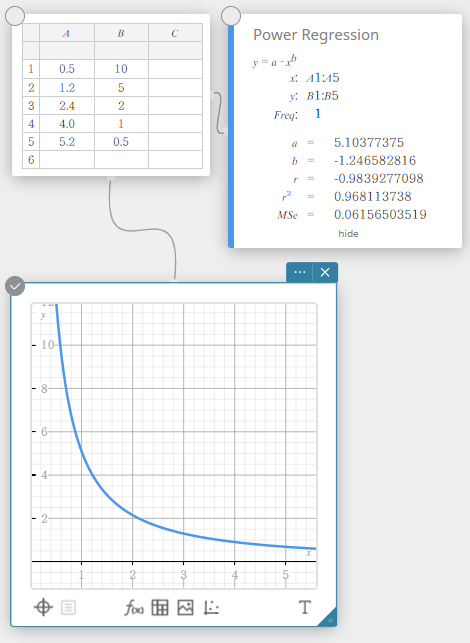
Power Regression
Power regression can be used when \(y\) is proportional to the power of \(x\). The normal power regression formula is \(y=a \cdot x^b\). If we obtain the natural logarithms of both sides, we get \(\ln(y)=\ln(a)+b \cdot \ln(x)\). Next, if we say that \(X=\ln(x)\), \(Y=\ln(y)\), and \(A=\ln(a)\), the formula corresponds to the linear regression formula \(Y=A+b \cdot X\).

\(y = a \cdot x^b\)
\(a\) … regression coefficient
\(b\) … regression power
\(r\) … correlation coefficient
\(r^2\) … coefficient of determination
\({\rm MSe}\) … mean square error

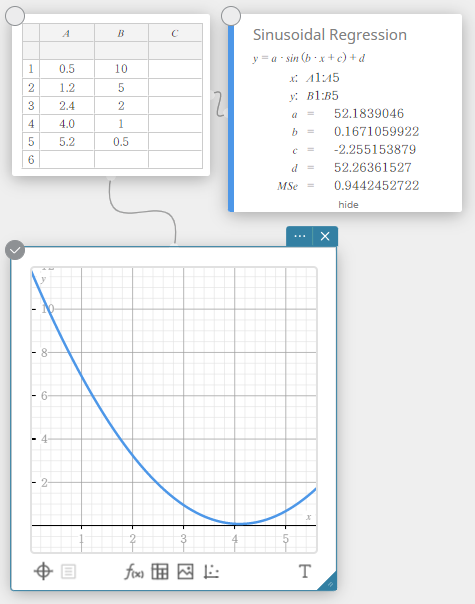
Sinusoidal Regression
Sinusoidal regression is best for data that repeats at a regular fixed interval over time.

\(y = a \cdot \sin( b \cdot x + c ) + d\)
\(a\), \(b\), \(c\), \(d\) … regression coefficient
\({\rm MSe}\) … mean square error

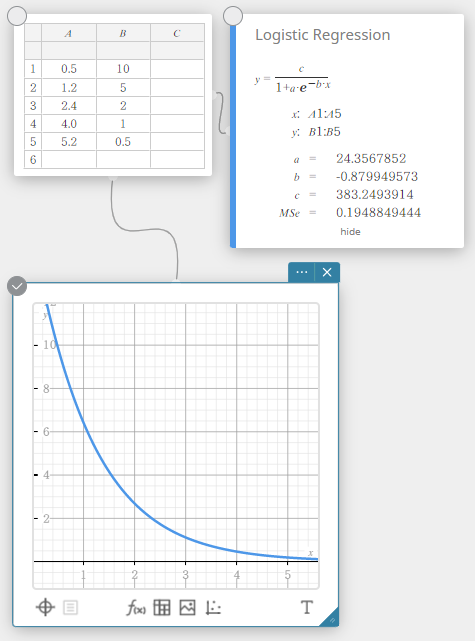
Logistic Regression
Logistic regression is best for data whose values continually increase over time, until a saturation point is reached.

\(\displaystyle y=\frac{c}{1+a \cdot e^{-b \cdot x}}\)
\(a\), \(b\), \(c\) … regression coefficient
\({\rm MSe}\) … mean square error

Tests

One-Sample Z-Test
Tests a single sample mean against the known mean of the null hypothesis when the population standard deviation is known. The normal distribution is used for the One-Sample Z-Test.

\(Z=\displaystyle \frac{\overline{x}-\mu_{0}}{\displaystyle \frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) : sample mean
\(\mu_{0}\) : assumed population mean
\(\sigma\) : population standard deviation
\(n\) : sample size

Data type: Variable

• Input Terms
  \( \mu \) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  \( \mu_{0} \) : assumed population mean
  \( \sigma \) : population standard deviation（\( \sigma > 0 \)）
  \(\overline{x}\) : sample mean
  \(n\) : sample size (positive integer)

• Output Terms
  \( \mu \neq \) : population mean value condition
  \(z\) : z value
  Prob : \(p\) value

Data type: List

• Input Terms
  \( \mu \) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  \( \mu_{0} \) : assumed population mean
  \( \sigma \) : population standard deviation （\( \sigma > 0 \)）
  List : data list
  Freq : frequency (1 or list name)

• Output Terms
  \( \mu \neq \) : population mean value condition
  \(z\) : \(z\) value
  Prob : \(p\) value
  \( \overline{x} \) : sample mean
  \( s_{x} \) : sample standard deviation
  \( n \) : sample size

Two-Sample Z-Test
Tests the difference between two means when the standard deviations of the two populations are known. The normal distribution is used for the Two-Sample Z-Test.

\( Z=\displaystyle \frac{ \overline{x}_{1} – \overline{x}_{2} }{ \sqrt{\displaystyle \frac{{\sigma_{1}}^2}{n_{1}} +\displaystyle \frac{{\sigma_{2}}^2}{n_{2}} } } \)

\( \overline{x}_{1} \) : sample mean of sample 1 data
\( \overline{x}_{2} \) : sample mean of sample 2 data
\( \sigma_{1} \) : population standard deviation of sample 1
\( \sigma_{2} \) : population standard deviation of sample 2
\( n_{1} \) : size of sample 1
\( n_{2} \) : size of sample 2

Data type: Variable

• Input Terms
  \( \mu_{1} \) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is less than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2).
  \( \sigma_{1} \) : population standard deviation of sample 1 （\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : population standard deviation of sample 2（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( n_{1} \) : size of sample 1 (positive integer)
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( n_{2} \) : size of sample 2 (positive integer)

• Output Terms
  \(z\) : z value
  Prob : \(p\) value

Data type: List

• Input Terms
  \( \mu_{1} \) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is less than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2).
  \( \sigma_{1} \) : population standard deviation of sample 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : population standard deviation of sample 2（\( \sigma_{2} > 0 \)）
  List(1) : list where sample 1 data is located
  List(2) : list where sample 2 data is located
  Freq(1) : frequency of sample 1 (1 or list name)
  Freq(2) : frequency of sample 2 (1 or list name)

• Output Terms
  \(z\) : z value
  Prob : \(p\) value
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( s_{x_{1}} \) : sample standard deviation of sample 1
  \( s_{x_{2}} \) : sample standard deviation of sample 2
  \( n_{1} \) : size of sample 1
  \( n_{2} \) : size of sample 2

One-Prop Z-Test (One-Proportion Z-Test)
Tests a single sample proportion against the known proportion of the null hypothesis. The normal distribution is used for the One-Proportion Z-Test.

\(Z =\displaystyle \frac{\displaystyle \frac{x}{n} – p_{0} }{ \sqrt{\displaystyle \frac{ p_{0}(1-p_{0}) }{n} }}\)
\(p_{0}\) : expected sample proportion
\(n\) : sample size

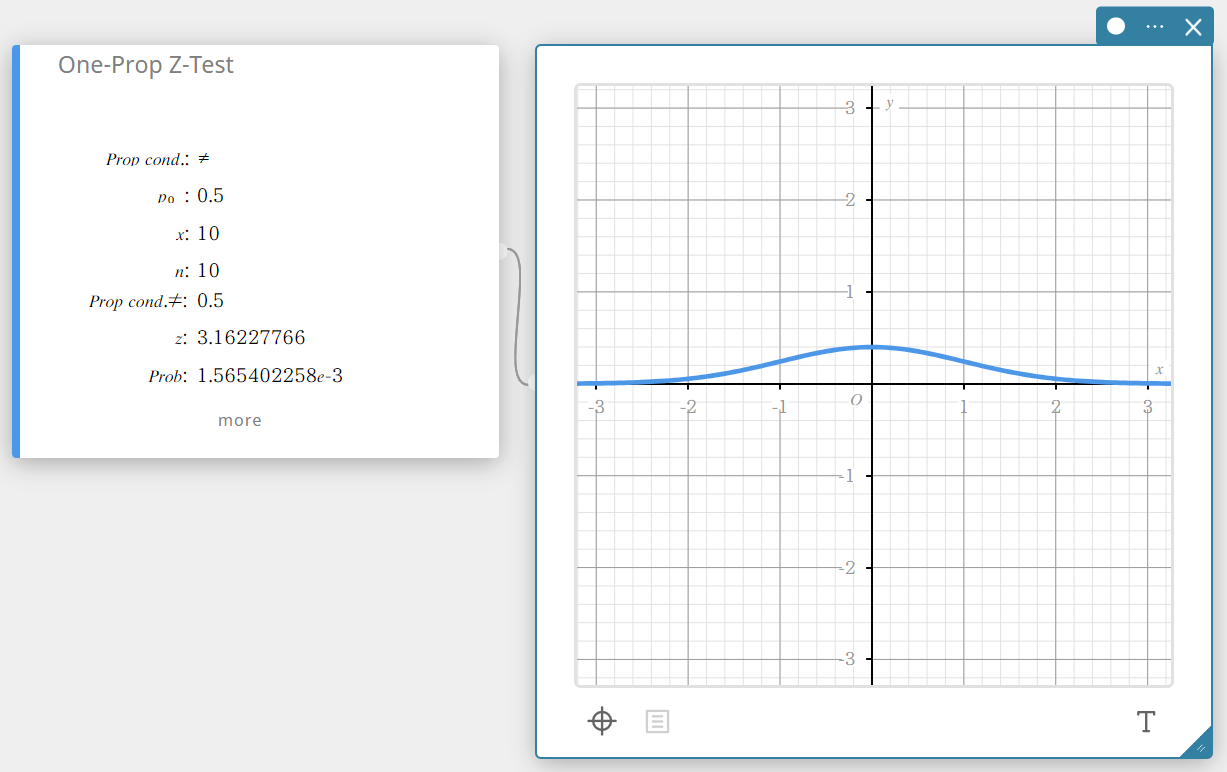
• Input Terms
  Prop cond : sample proportion test condition (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  \(p_{0}\) : expected sample proportion（\( 0 < p_{0} < 1 \)）
  \(x\) : sample value (integer, \( x \geq 0 \)）
  \(n\) : sample size (positive integer)

• Output Terms
  Prop Cond \(\neq\) : sample proportion test condition
  \(z\) : z value
  Prob : \(p\) value
  \(\hat{p}\) : estimated sample proportion

Two-Prop Z-Test (Two-Proportion Z-Test)
Tests the difference between two sample proportions. The normal distribution is used for the Two-Proportion Z-Test.

\( Z =\displaystyle \frac{\displaystyle \frac{x_{1}}{n_{1}} -\displaystyle \frac{x_{2}}{n_{2}} }{ \sqrt{ \hat{p} \left(1-\hat{p} \right) \left(\displaystyle \frac{1}{n_{1}} +\displaystyle \frac{1}{n_{2}} \right) } }\)
\(x_{1}\) : data value of sample 1
\(x_{2}\) : data value of sample 2
\(n_{1}\) : size of sample 1
\(n_{2}\) : size of sample 2
\(\hat{p}\) : estimated sample proportion

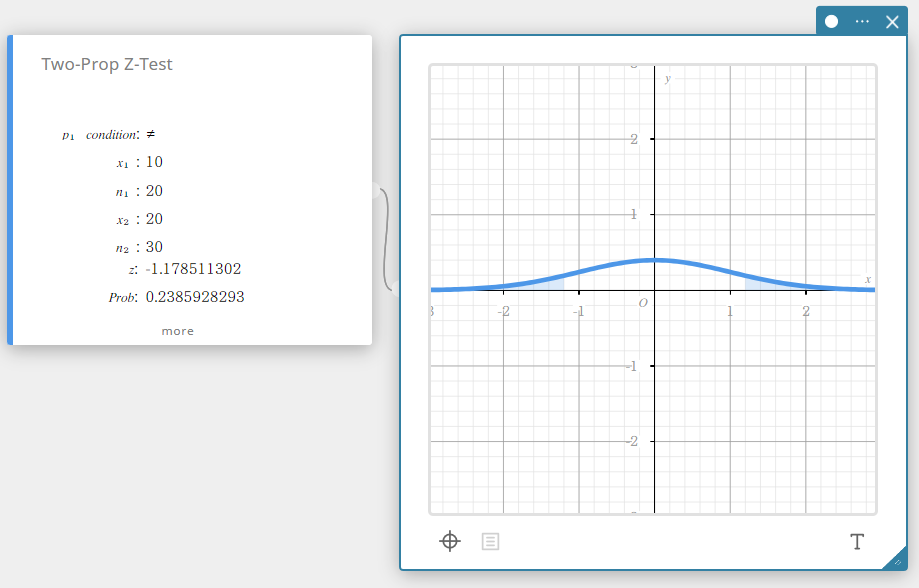
• Input Terms
  \(p_{1}\) condition : sample proportion test conditions (“\(\neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is smaller than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2.)
  \(x_{1}\) : data value of sample 1 (integer, \(x_{1}\) must be less than or equal to \(n_{1}\))
  \(n_{1}\) : size of sample 1 (positive integer)
  \(x_{2}\) : data value of sample 2 (integer, \(x_{2}\) must be less than or equal to \(n_{2}\))
  \(n_{2}\) : size of sample 2 (positive integer)

• Output Terms
  \(z\) : z value
  Prob : \(p\) value
  \(\hat{p}_{1}\) : estimated proportion of sample 1
  \(\hat{p}_{2}\) : estimated proportion of sample 2
  \(\hat{p}\) : estimated sample proportion

One-Sample \(t\) -Test
Tests a single sample mean against the known mean of the null hypothesis when the population standard deviation is unknown. The \(t\) distribution is used for the One-Sample \(t\)-Test.

\(t =\displaystyle \frac{ \overline{x} – \mu_{0} }{\displaystyle \frac{ s_{x} }{ \sqrt{n} } }\)
\(\overline{x}\) : sample mean
\(\mu_{0}\) : assumed population mean
\(s_{x}\) : sample standard deviation
\(n\) : sample size

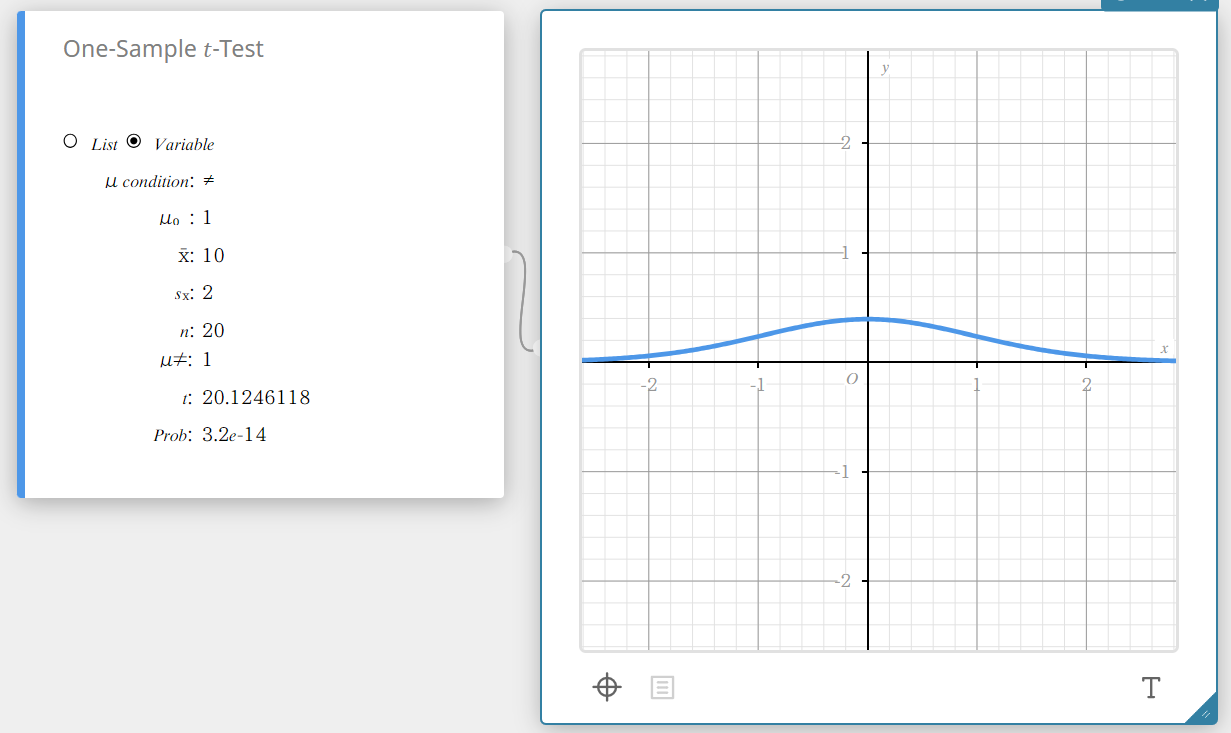
Data type: Variable

• Input Terms
  \(\mu\) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  \(\mu_{0}\) : assumed population mean
  \(\overline{x}\) : sample mean
  \(s_{x}\) : sample standard deviation（\( s_{x} > 0 \)）
  \(n\) : sample size (positive integer)

• Output Terms
  \(\mu \ne\) : population mean value test conditions
  \(t\) : \(t\) value
  Prob : \(p\) value

Data type: List

• Input Terms
  \(\mu\) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  \(\mu_{0}\) : assumed population mean
  List : data list
  Freq : frequency (1 or list name)

• Output Terms
  \(\mu \ne\) : population mean value test conditions
  \(t\) : \(t\) value
  Prob : \(p\) value
  \(\overline{x}\) : sample mean
  \(s_{x}\) : sample standard deviation
  \(n\) : sample size

Two-Sample \(t\) -Test
Tests the difference between two means when the standard deviations of the two populations are unknown. The \(t\) distribution is used for the Two-Sample \(t\)-Test.

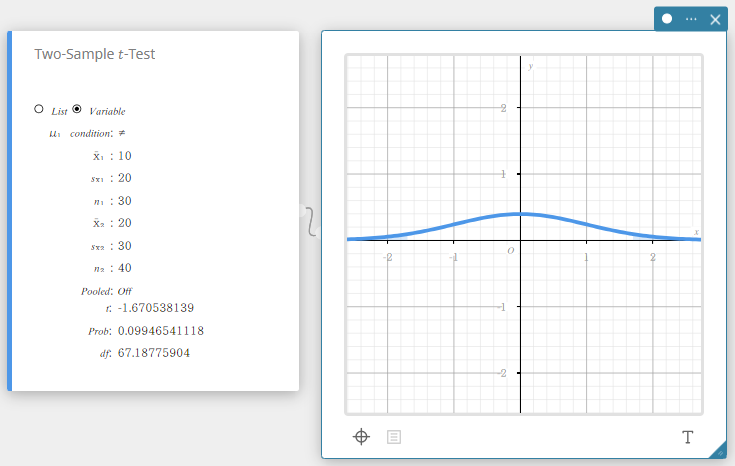
• When the two population standard deviations are equal (pooled)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{{s_{p}}^2 \left(\displaystyle \frac{1}{n_1} + \displaystyle \frac{1}{n_2} \right)}}\)
  \(df=n_1+n_2-2\)
  \(s_p=\sqrt{ \displaystyle \frac{(n_1-1){s_{x_1}}^2 + (n_2-1){s_{x_2}}^2}{n_1+n_2-2} }\)

• When the two population standard deviations are not equal (not pooled)
  \(t=\displaystyle \frac{\overline{x}_1-\overline{x}_2}{\sqrt{\displaystyle \frac{{s_{x_1}}^2}{n_1} + \displaystyle \frac{{s_{x_2}}^2}{n_2}}}\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{(1-C)^2}{n_2-1}}\)
  \(C =\displaystyle \frac{\displaystyle \frac{{s_{x_1}}^2}{n_1}}{\displaystyle \frac{{s_{x_1}}^2}{n_1} +\displaystyle \frac{{s_{x_2}}^2}{n_2}}\)

\(x_1\): sample mean of sample 1 data
\(x_2\): sample mean of sample 2 data
\(s_{x_1}\) : sample standard deviation of sample 1
\(s_{x_2}\) : sample standard deviation of sample 2
\(s_p\) : pooled sample standard deviation
\(n_1\) : size of sample 1
\(n_2\) : size of sample 2

Data type: Variable

• Input Terms
  \(\mu_1\) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is smaller than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2.)
  \(\overline{x}_1\) : sample mean of sample 1 data
  \(s_{x_1}\) : sample standard deviation of sample 1（\(s_{x_1} > 0\)）
  \(n_1\) : size of sample 1 (positive integer)
  \(\overline{x}_2\) : sample mean of sample 2 data
  \(s_{x_2}\) : sample standard deviation of sample 2（\(s_{x_2} > 0\)）
  \(n_2\) : size of sample 2 (positive integer)

• Output Terms
  \(t\) : \(t\) value
  Prob : \(p\) value
  \(df\) : degrees of freedom
  \(s_p\) : pooled sample standard deviation

Data type: List

• Input Terms
  \(\mu_1\) condition : population mean value test conditions (“\(\neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is smaller than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2.)
  List(1) : list where sample 1 data is located
  List(2) : list where sample 2 data is located
  Freq(1) : frequency of sample 1 (1 or list name)
  Freq(2) : frequency of sample 2 (1 or list name)
  Pooled : On (equal variances) or Off (unequal variances)

• Output Terms
  \(t\) : \(t\) value
  Prob : \(p\) value
  \(df\) : degrees of freedom
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( s_{x_{1}} \) : sample standard deviation of sample 1
  \( s_{x_{2}} \) : sample standard deviation of sample 2
  \(s_p\) : pooled sample standard deviation
  \( n_{1} \) : size of sample 1
  \( n_{2} \) : size of sample 2

Linear Reg \(t\) -Test (Linear Regression \(t\) -Test)
Tests the linear relationship between the paired variables ( x , y ). The method of least squares is used to determine a and b , which are the coefficients of the regression formula \(y = a + b \cdot x\). The p -value is the probability of the sample regression slope ( b ) provided that the null hypothesis is true, \(\beta = 0\). The t distribution is used for the Linear Regression \(t\)-Test.

\(t=r\sqrt{\displaystyle \frac{n-2}{1-r^2}}\)
\( \displaystyle b=\left\{ \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y}) \right\} / \left\{\sum_{i=1}^n (x_i-\overline{x})^2 \right\}\)
\(a=\overline{y}-b\overline{x}\)

\(a\) : regression constant term (y-intercept)
\(b\) : regression coefficient (slope)
\(n\) : sample size（\(n \ge 3\)）
\(r\) : correlation coefficient
\(r^2\) : coefficient of determination

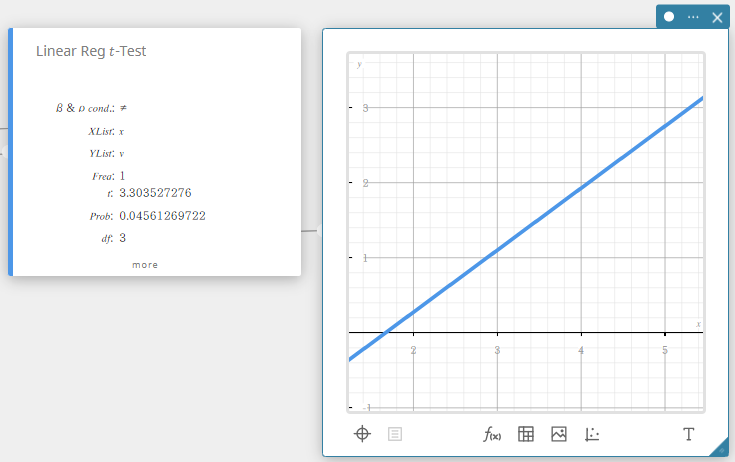
• Input Terms
  \(\beta\ \&\ \rho\) cond : test conditions (“\(\neq\)” specifies two-tail test, “<” specifies lower one-tail test, “>” specifies upper one-tail test.)
  XList : x -data list
  YList : y -data list
  Freq : frequency (1 or list name)

• Output Terms
  \(t\) : \(t\) value
  Prob : \(p\) value
  \(df\) : degrees of freedom
  \(a\) : regression constant term (y-intercept)
  \(b\) : regression coefficient (slope)
  se : standard error of estimate about the least-squares regression line
  \(r\) : correlation coefficient
  \(r^2\) : coefficient of determination
  SEb: standard error of the least squares slope

\(\chi^2\) Test
Tests the independence of two categorical variables arranged in matrix form. The \(\chi^2\) test for independence compares the observed matrix to the expected theoretical matrix. The \(\chi^2\) distribution is used for the \(\chi^2\) test.

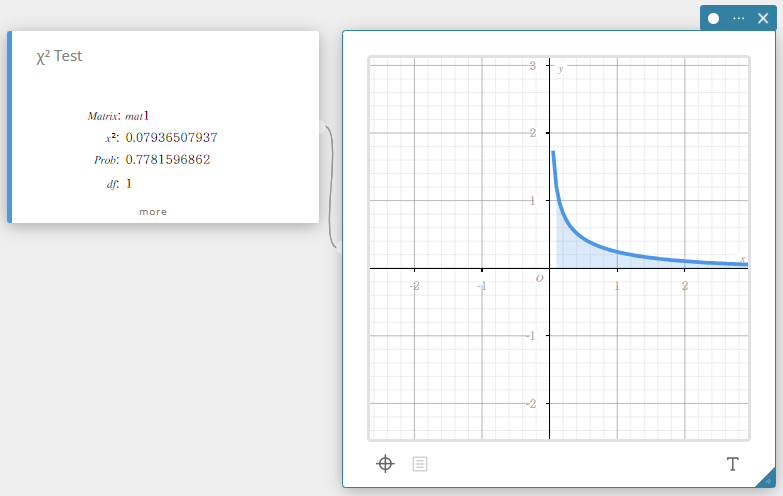
MEMO
The minimum size of the matrix is 1×2. An error occurs if the matrix has only one column.
The result of the expected frequency calculation is stored in the system variable named “Expected”.

\( \chi^2 = \sum_{i=1}^{k}\sum_{j=1}^{l} \displaystyle \frac{(x_{ij}-F_{ij})^2}{F_{ij}} \)
\( F_{ij}=\frac{{\displaystyle\sum_{i=1}^k}x_{ij}\times{\displaystyle\sum_{j=1}^lx_{ij}}}{{\displaystyle\sum_{i=1}^k}{\displaystyle\sum_{j=1}^l}x_{ij}} \)
\( x_{ij}\) : The element at row i , column j of the observed matrix
\( F_{ij}\) : The element at row i , column j of the expected matrix

• Input Terms
  Matrix: name of matrix containing observed values (positive integers in all cells for 2×2 and larger matrices; positive real numbers for one row matrices)

• Output Terms
  \(\chi^2\) : \(\chi^2\) value
  Prob : \(p\) value
  \(df\) : degrees of freedom
  Observed : the input matrix of observed values
  Expected : the calculated matrix of expected values

\(\chi^2\) GOF Test (\(\chi^2\) Goodness-Of-Fit Test)
Tests whether the observed count of sample data fits a certain distribution. For example, it can be used to determine conformance with normal distribution or binomial distribution.


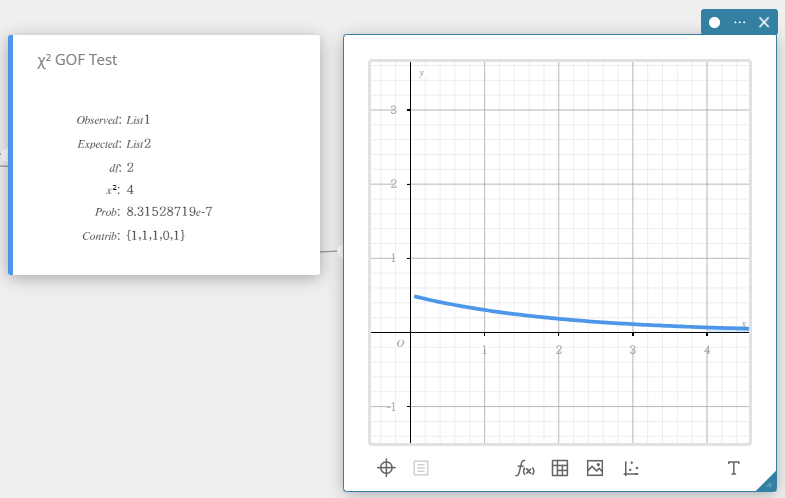
\(\chi^2=\sum_i^k \displaystyle \frac{ (O_i – E_i )^2 }{E_i}\)
\(Contrib = \left\{\displaystyle \frac{ (O_1 – E_1 )^2 }{E_1} \ \displaystyle \frac{ (O_2 – E_2 )^2 }{E_2} \cdots \displaystyle \frac{ (O_k – E_k )^2 }{E_k} \right\} \)

\(O_i\) : The i-th element of the observed list
\(E_i\) : The i-th element of the expected list

• Input Terms
  Observed list : name of list containing observed counts (all cells positive integers)
  Expected list : name of list that is for saving expected frequency
  \(df\) : degrees of freedom

• Output Terms
  \(\chi^2\) : \(\chi^2\) value
  Prob : \(p\) value
  \(df\) : degrees of freedom
  Contrib : name of list specifying the contribution of each observed count

Two-Sample F-Test
Tests the ratio between sample variances of two independent random samples. The F distribution is used for the Two-Sample F-Test.

\( F=\displaystyle \frac{{S_{x_1}}^2}{{S_{x_2}}^2}\)

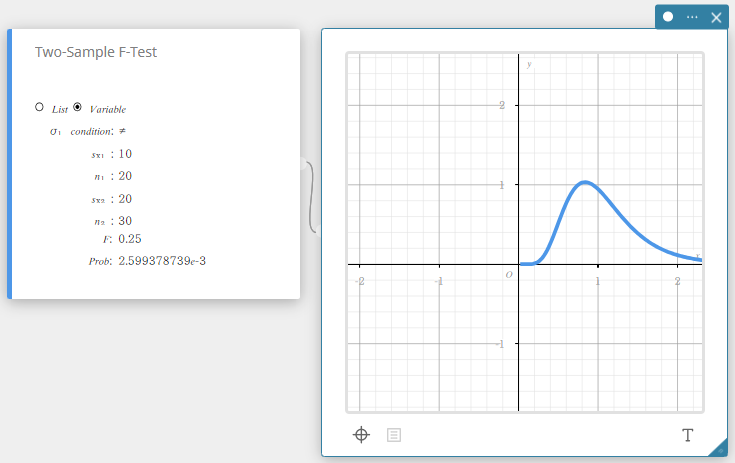
Data type: Variable

• Input Terms
  \( \sigma_1\) condition: population standard deviation test conditions (“\( \neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is smaller than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2.)
  \( s_{x_1}\) : sample standard deviation of sample 1（ \( s_{x_1} > 0\)）
  \( n_1\) : size of sample 1 (positive integer)
  \( s_{x_2}\) : sample standard deviation of sample 2（ \( s_{x_2} > 0\)）
  \( n_2\) : size of sample 2 (positive integer)

• Output Terms
  \( F\) : F value
  Prob : p value

Data type: List

• Input Terms
  \( \sigma_1\) condition: population standard deviation test conditions (“\( \neq\)” specifies two-tail test, “<” specifies one-tail test where sample 1 is smaller than sample 2, “>” specifies one-tail test where sample 1 is greater than sample 2.)
  List(1) : list where sample 1 data is located
  List(2) : list where sample 2 data is located
  Freq(1) : frequency of sample 1 (1 or list name)
  Freq(2) : frequency of sample 2 (1 or list name)

• Output Terms
  \( F\) : F value
  Prob : p value
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( s_{x_{1}} \) : sample standard deviation of sample 1
  \( s_{x_{2}} \) : sample standard deviation of sample 2
  \( n_{1} \) : size of sample 1
  \( n_{2} \) : size of sample 2

One-Way ANOVA (One-Way analysis of variance)
Tests the hypothesis that the population means of multiple populations are equal. It compares the mean of one or more groups based on one independent variable or factor.

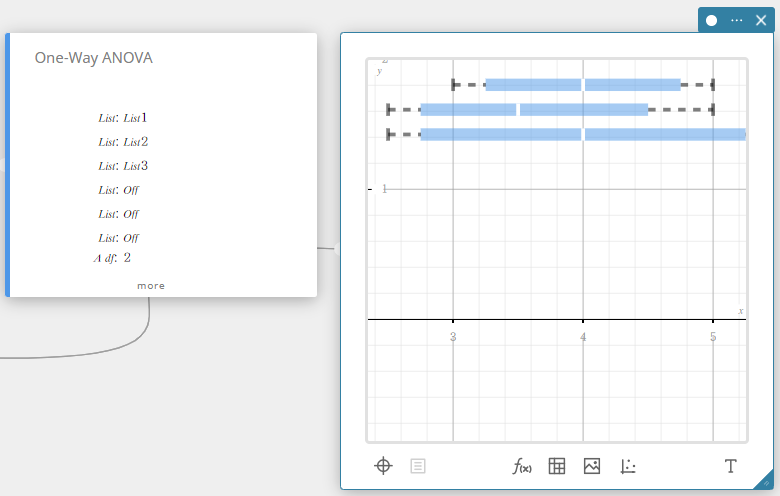
• Input Terms
  FactorList(A) : list where levels of Factor A are located
  DependentList : list where sample data is located

• Output Terms
  A df : degrees of freedom of Factor A
  A MS : mean square of Factor A
  A SS : sum of squares of Factor A
  A F : F value of Factor A
  A p : p value of Factor A
  Err df : degrees of freedom of error
  Err MS : mean square of error
  Err SS : sum of squares of error

Two-Way ANOVA (Two-Way analysis of variance)
Tests the hypothesis that the population means of multiple populations are equal. It examines the effect of each variable independently as well as their interaction with each other based on a dependent variable.

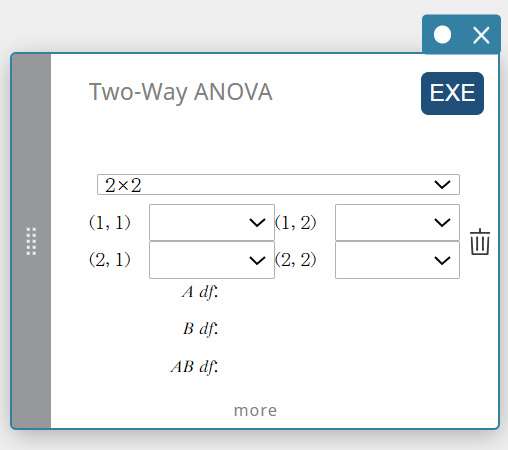
• Input Terms
  2×2: data table type
  FactorList(A) : list where levels of Factor A are located
  FactorList(B) : list where levels of Factor B are located
  DependentList : list where sample data is located

• Output Terms
  A df : degrees of freedom of Factor A
  A MS : mean square of Factor A
  A SS : sum of squares of Factor A
  A F : F value of Factor A
  A p : p value of Factor A
  B df : degrees of freedom of Factor B
  B MS : mean square of Factor B
  B SS : sum of squares of Factor B
  B F : F value of Factor B
  B p : p value of Factor B
  AB df : degrees of freedom of Factor A × Factor B
  AB MS : mean square of Factor A × Factor B
  AB SS : sum of squares of Factor A × Factor B
  AB F : F value of Factor A × Factor B
  AB p : p value of Factor A × Factor B
  Err df : degrees of freedom of error
  Err MS : mean square of error
  Err SS : sum of squares of error

Confidence Intervals

One-Sample Z Interval
Calculates the confidence interval for the population mean based on a sample mean and known population standard deviation.

\(Lower = \overline{x}-Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(Upper = \overline{x}+Z \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{\sigma}{\sqrt{n}}\)
\(\alpha\) is the significance level, and \(100(1 – \alpha)\%\) is the confidence level. When the confidence level is \(95\%\), for example, you would input 0.95, which produces α = 1 – 0.95 = 0.05.

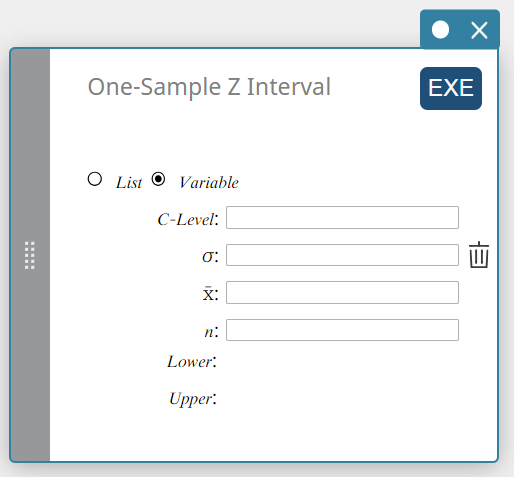
Data type: Variable

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : population standard deviation（\( \sigma > 0 \)）
  \( \overline{x} \) : sample mean
  \( n \) : sample size (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)

Data type: List

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma \) : population standard deviation（\( \sigma > 0 \)）
  List: list where sample data is located
  Freq : frequency of sample (1 or list name)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \( \overline{x} \) : sample mean
  \( s_{x} \) : sample standard deviation
  \( n \) : sample size

Two-Sample Z Interval
Calculates the confidence interval for the difference between population means based on the difference between sample means when the population standard deviations are known.


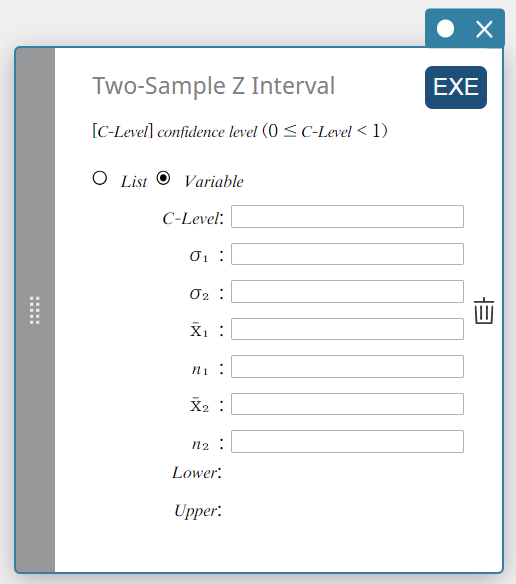
\(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)
\(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{{\sigma_1}^2}{n_1} + \displaystyle \frac{{\sigma_2}^2}{n_2} }\)

Data type: Variable

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : population standard deviation of sample 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : population standard deviation of sample 2（\( \sigma_{2} > 0 \)）
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( n_{1} \) : size of sample 1 (positive integer)
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( n_{2} \) : size of sample 2 (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)

Data type: List

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \sigma_{1} \) : population standard deviation of sample 1（\( \sigma_{1} > 0 \)）
  \( \sigma_{2} \) : population standard deviation of sample 2（\( \sigma_{2} > 0 \)）
  List(1) : list where sample 1 data is located
  List(2) : list where sample 2 data is located
  Freq(1) : frequency of sample 1 (1 or list name)
  Freq(2) : frequency of sample 2 (1 or list name)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( s_{x_{1}} \) : sample standard deviation of sample 1
  \( s_{x_{2}} \) : sample standard deviation of sample 2
  \( n_{1} \) : size of sample 1
  \( n_{2} \) : size of sample 2

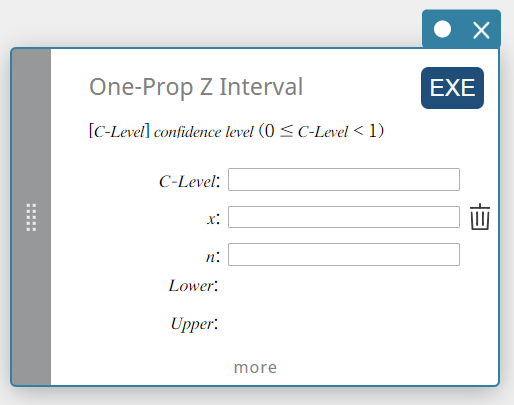
One-Prop Z Interval (One-Proportion Z Interval)
Calculates the confidence interval for the population proportion based on a single sample proportion.


\(Lower =\displaystyle \frac{x}{n}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)
\(Upper =\displaystyle \frac{x}{n}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{1}{n} \left(\displaystyle \frac{x}{n} \left( 1- \displaystyle \frac{x}{n} \right) \right) }\)

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( x \) : data (0 or positive integer)
  \( n \) : sample size (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \(\hat{p}\) : estimated sample proportion

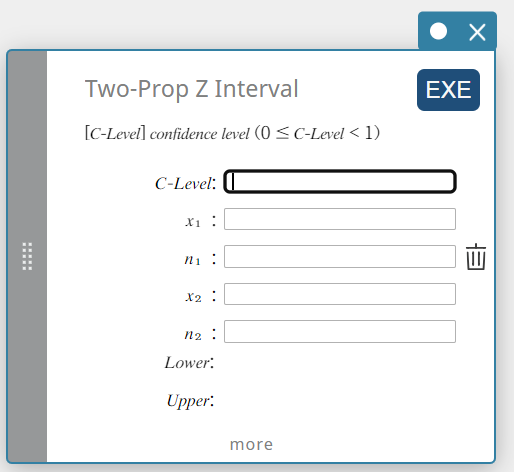
Two-Prop Z Interval (Two-Proportion Z Interval)
Calculates the confidence interval for the difference between population proportions based on the difference between Two-Proportion Z Interval.


\( Lower =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}-Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{\displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1- \displaystyle\frac{x_1}{n_1} \right) }{n_1} + \displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1- \displaystyle \frac{x_2}{n_2} \right) }{n_2} } \)
\( Upper =\displaystyle \frac{x_1}{n_1}- \displaystyle \frac{x_2}{n_2}+Z \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \displaystyle \frac{\displaystyle \frac{x_1}{n_1} \left( 1-\displaystyle \frac{x_1}{n_1} \right) }{n_1} +\displaystyle \frac{\displaystyle \frac{x_2}{n_2} \left( 1-\displaystyle\frac{x_2}{n_2} \right) }{n_2} } \)

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \(x_{1}\) : data value of sample 1 (integer, \(x_{1}\) must be less than or equal to \(n_{1}\))
  \(n_{1}\) : size of sample 1 (positive integer)
  \(x_{2}\) : data value of sample 2 (integer, \(x_{2}\) must be less than or equal to \(n_{2}\))
  \(n_{2}\) : size of sample 2 (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \(\hat{p}_{1}\) : estimated proportion of sample 1
  \(\hat{p}_{2}\) : estimated proportion of sample 2

One-Sample \(t\) Interval
Calculates the confidence interval for the population mean based on a sample mean and a sample standard deviation when the population standard deviation is not known.

\(Lower = \overline{x}-t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)
\(Upper = \overline{x}+t_{n-1} \left(\displaystyle \frac{\alpha}{2} \right) \displaystyle \frac{s_x}{\sqrt{n}}\)

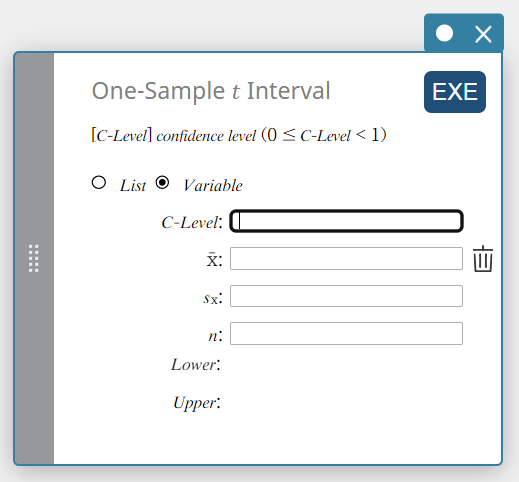
Data type: Variable

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x} \) : sample mean
  \(s_{x}\) : sample standard deviation（\( s_{x} \ge 0 \)）
  \(n\) : sample size (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)

Data type: List

• Input Terms
  C-Level : confidence leve（\(0 \le\) C-Level \(\lt 1\)）
  List: list where sample data is located
  Freq : frequency of sample (1 or list name)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \( \overline{x} \) : sample mean
  \( s_{x} \) : sample standard deviation
  \( n \) : sample size

Two-Sample \(t\) Interval
Calculates the confidence interval for the difference between population means based on the difference between sample means and sample standard deviations when the population standard deviations are not known.

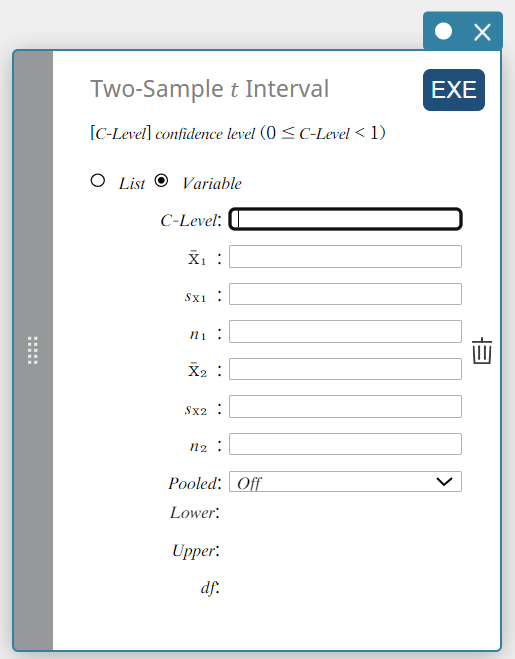
• When the two population standard deviations are equal (pooled)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{n_1+n_2-2} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{{s_p}^2 \left(\displaystyle \frac{1}{n_1}+ \displaystyle \frac{1}{n_2} \right) }\)
  

• When the two population standard deviations are not equal (not pooled)
  
  \(Lower = \left( \overline{x}_1-\overline{x}_2 \right) -t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(Upper = \left( \overline{x}_1-\overline{x}_2 \right) +t_{df} \left(\displaystyle \frac{\alpha}{2} \right) \sqrt{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1}+ \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  \(df =\displaystyle \frac{1}{\displaystyle \frac{C^2}{n_1-1} + \displaystyle \frac{ \left( 1-C \right) ^2}{n_2-1}}\)
  \(C=\displaystyle \frac{\displaystyle \frac{{S_{x_1}}^2}{n_1}}{ \left(\displaystyle \frac{{S_{x_1}}^2}{n_1} + \displaystyle \frac{{S_{x_2}}^2}{n_2} \right) }\)
  

Data type: Variable

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \(s_{x_1}\) : sample standard deviation of sample 1（\(s_{x_1} \ge 0\)）
  \( n_{1} \) : size of sample 1 (positive integer)
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \(s_{x_2}\) : sample standard deviation of sample 2（\(s_{x_2} \ge 0\)）
  \( n_{2} \) : size of sample 2 (positive integer)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \(df\) : degrees of freedom
  \(s_p\) : pooled sample standard deviation

Data type: List

• Input Terms
  C-Level : confidence level（\(0 \le\) C-Level \(\lt 1\)）
  List(1) : list where sample 1 data is located
  List(2) : list where sample 2 data is located
  Freq(1) : frequency of sample 1 (1 or list name)
  Freq(2) : frequency of sample 2 (1 or list name)
  Pooled : On (equal variances) or Off (unequal variances)

• Output Terms
  Lower : interval lower limit (left edge)
  Upper : interval upper limit (right edge)
  \(df\) : degrees of freedom
  \( \overline{x}_{1} \) : sample mean of sample 1 data
  \( \overline{x}_{2} \) : sample mean of sample 2 data
  \( s_{x_{1}} \) : sample standard deviation of sample 1
  \( s_{x_{2}} \) : sample standard deviation of sample 2
  \(s_p\) : pooled sample standard deviation
  \( n_{1} \) : size of sample 1
  \( n_{2} \) : size of sample 2

Distribution

Normal PD (Normal Probability Density)
Calculates the normal probability density for a specified value.
Specifying σ = 1 and μ= 0 produces standard normal distribution.

\(\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\displaystyle -\frac{(x-\mu)^2}{2\sigma^2}} \qquad (\sigma>0)\)

• Input Terms
  \( x \) : data value
  \( \sigma \) : population standard deviation (\( \sigma > 0 \)）
  \( \mu \) : population mean

• Output Terms
  Prob : normal probability density

Normal CD (Normal Cumulative Distribution)
Calculates the cumulative probability of a normal distribution between a lower bound ( a ) and an upper bound ( b ).

\(\displaystyle p=\frac{1}{\sqrt{2\pi}\sigma}\int_a^b e^{ \scriptscriptstyle -\frac{(x-\mu)^2}{2\sigma^2} }dx\)

• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \( \sigma \) : population standard deviation (\( \sigma > 0 \)）
  \(\mu\) : population mean

• Output Terms
  Prob : normal distribution probability p
  z Low : standardized lower limit z value
  z Up : standardized upper limit z value

Student’s \(t\) PD (Student’s \(t\) Probability Density)
Calculates the Student’s t probability density for a specified value.


\(f(x)=\frac{\Gamma\left({\displaystyle\frac{df+1}2}\right)}{\Gamma\left({\displaystyle\frac{df}2}\right)}\times\frac{\left(1+{\displaystyle\frac{x^2}{df}}\right)^{-{\displaystyle\frac{df+1}2}}}{\sqrt{\pi\cdot df}}\)

• Input Terms
  \( x \) : data value
  \(df\) : degrees of freedom（\(df \gt 0\)）

• Output Terms
  Prob : Student’s t probability density

Student’s \(t\) CD (Student’s \(t\) Cumulative Distribution)
Calculates the cumulative probability of a Student’s t distribution between a lower bound ( a ) and an upper bound ( b ).


\( p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{df+1}{2} \right) }{\Gamma \left(\displaystyle \frac{df}{2} \right) \sqrt{\pi \cdot df}}\int_a^b \left(\displaystyle 1+\frac{x^2}{df} \right) ^{-\displaystyle\frac{df+1}{2}}dx \)

• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \(df\) : degrees of freedom（\(df \gt 0\)）

• Output Terms
  Prob : Student’s t distribution
  t Low : lower bound value you input
  t Up : upper bound value you input

\(\chi^2\) PD (\(\chi^2\) Probability Density)
Calculates the \(\chi^2\) probability density for a specified value.


\(f \left( x \right) =\displaystyle\frac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}\)

• Input Terms
  \( x \) : data value
  \(df\) : degrees of freedom (positive integer)

• Output Terms
  Prob : \(\chi^2\) probability density

\(\chi^2\) CD (\(\chi^2\) Cumulative Distribution)
Calculates the cumulative probability of a \(\chi^2\) distribution between a lower bound and an upper bound.


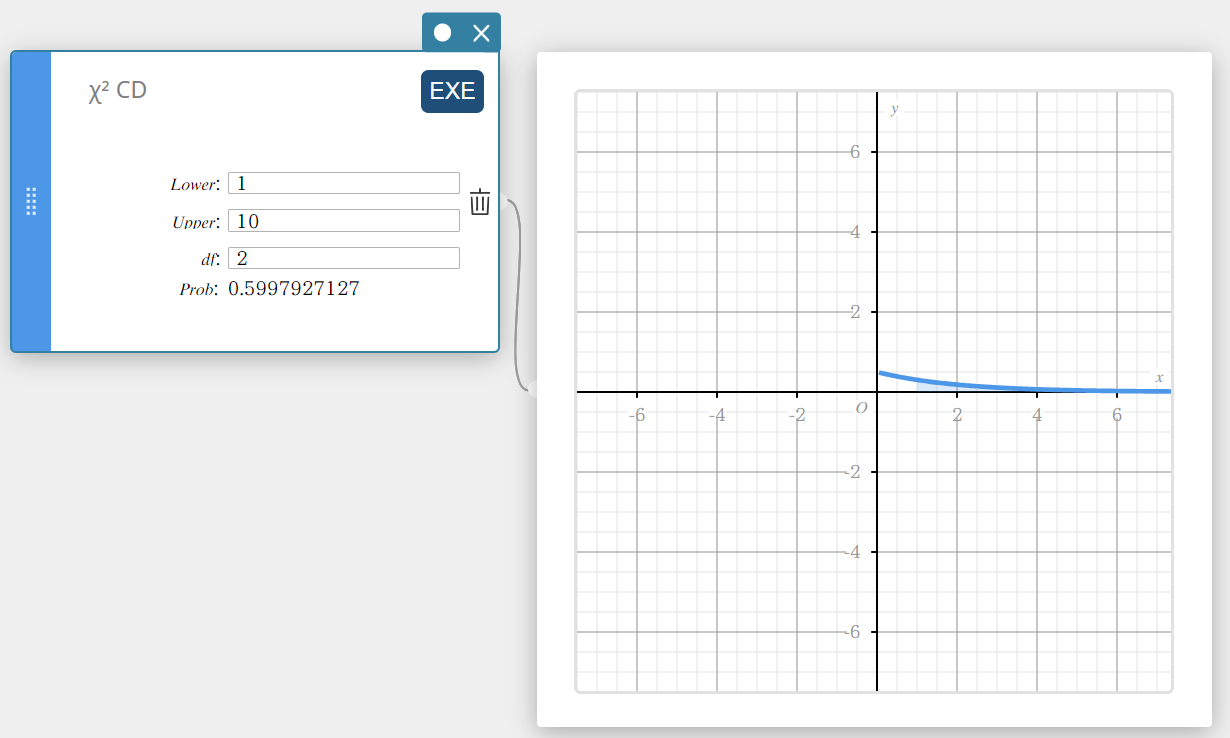
\(p=\cfrac{1}{\Gamma \left(\displaystyle \frac{df}{2} \right) } \left(\displaystyle \frac{1}{2} \right) ^{\displaystyle\frac{df}{2}}\int_a^b x^{\displaystyle\frac{df}{2}-1}e^{-\displaystyle\frac{x}{2}}dx\)

• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \(df\) : degrees of freedom (positive integer)

• Output Terms
  Prob : \(\chi^2\) distribution probability

F PD (F Probability Density)
Calculates the F probability density for a specified value.


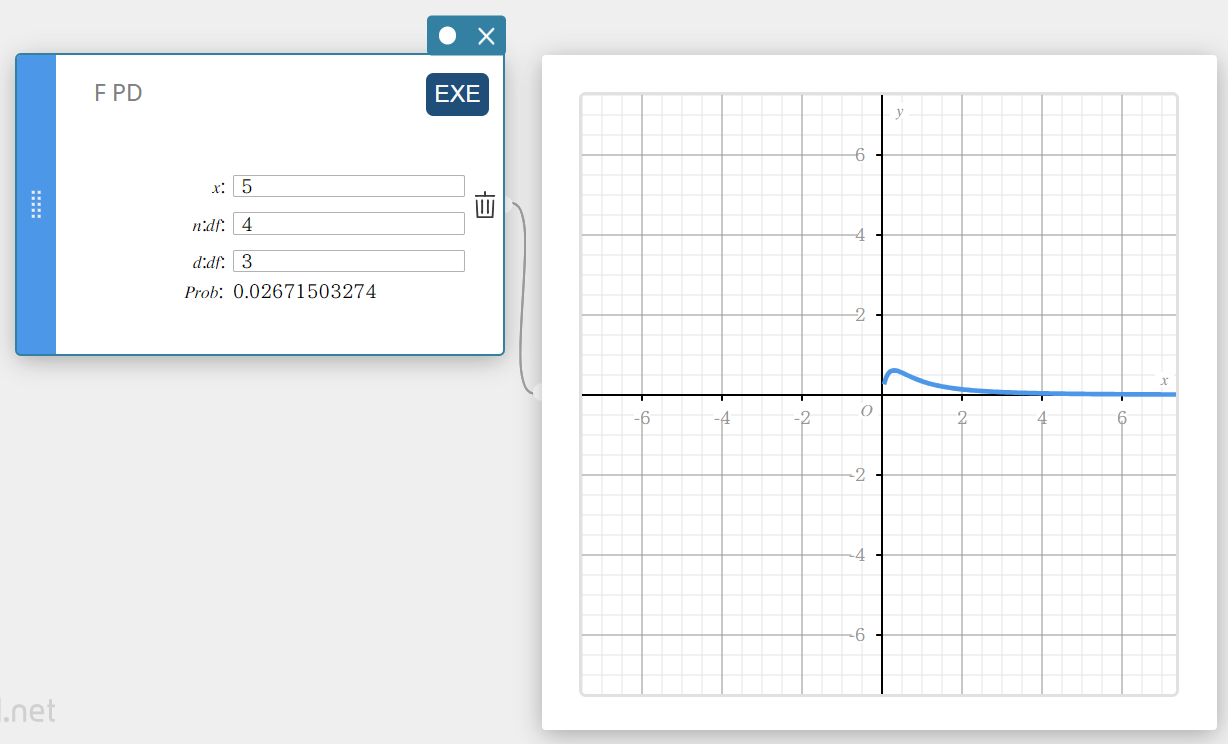
\(f(x)=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}\)

• Input Terms
  \( x \) : data value
  \( n:df \) : degrees of freedom of numerator (positive integer)
  \( d:df \) : degrees of freedom of denominator (positive integer)

• Output Terms
  Prob : F probability density

F CD (F Cumulative Distribution)
Calculates the cumulative probability of anF distribution between a lower bound and an upper bound.


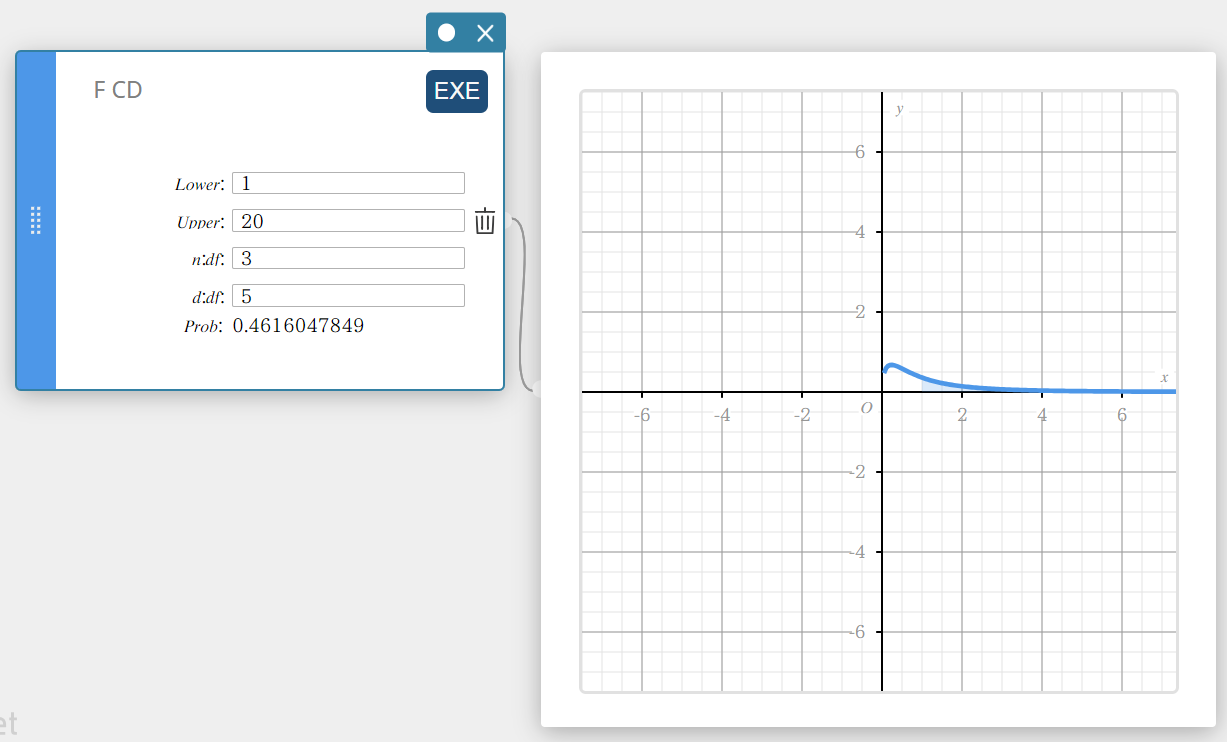
\(p=\displaystyle\frac{\Gamma \left(\displaystyle \frac{n+d}{2} \right) }{\Gamma \left(\displaystyle \frac{n}{2} \right) \Gamma \left(\displaystyle \frac{d}{2} \right) } \left(\displaystyle \frac{n}{d} \right) ^{\displaystyle\frac{n}{2}}\int_a^b x^{\displaystyle\frac{n}{2}-1} \left( 1+ \displaystyle\frac{n \cdot x}{d} \right) ^{- \displaystyle\frac{n+d}{2}}dx\)

• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \( n:df \) : degrees of freedom of numerator (positive integer)
  \( d:df \) : degrees of freedom of denominator (positive integer)

• Output Terms
  Prob : F distribution probability

Binomial PD (Binomial Distribution Probability)
Calculates the probability in a binomial distribution that success will occur on a specified trial.


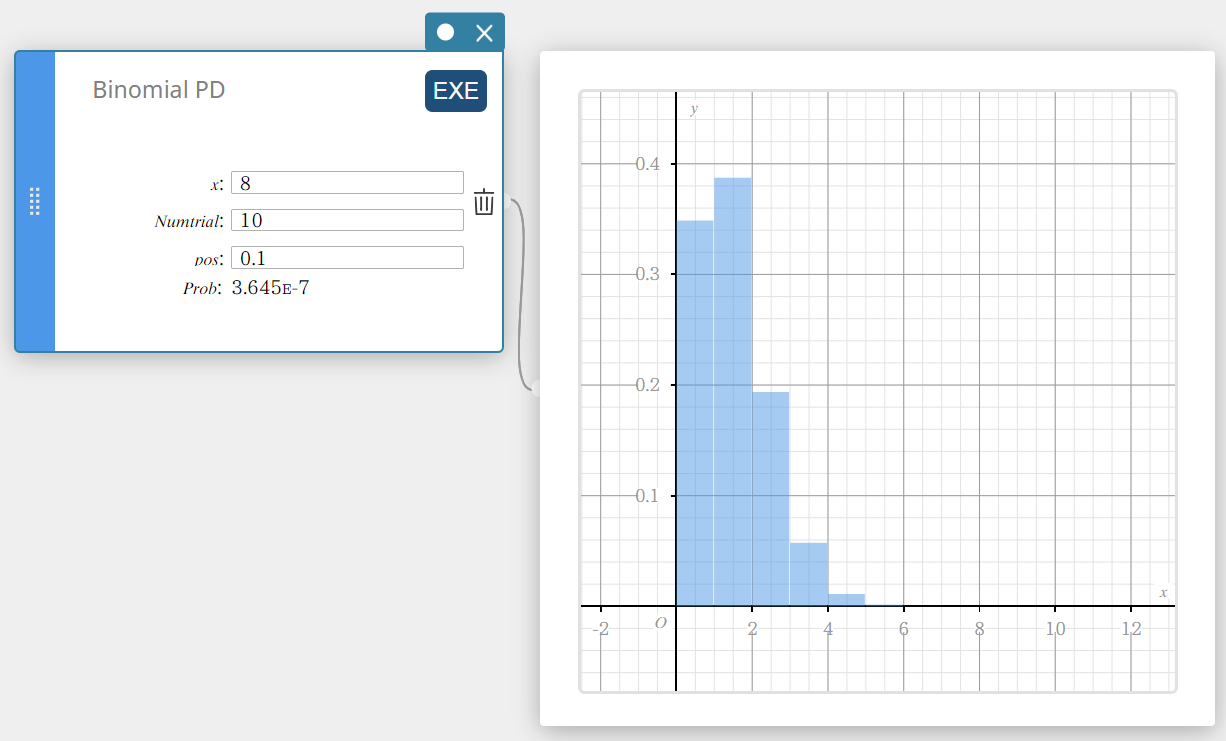
\(f(x)={}_nC_xp^x(1-p)^{n-x} \quad (x=0,1, \cdots,n)\)

\(p\) : probability of success（(0 \(≤\) p \(≤\) 1)
\(n\) : number of trials

• Input Terms
  \( x \) : specified trial (integer from 0 to n)
  Numtrial : number of trials n (integer, n ≥ 0)
  pos : probability of success p (0 \(≤\) p \(≤\) 1)

• Output Terms
  Prob : binomial probability

Binomial CD (Binomial Cumulative Distribution)
Calculates the cumulative probability in a binomial distribution that success will occur on or before a specified trial.

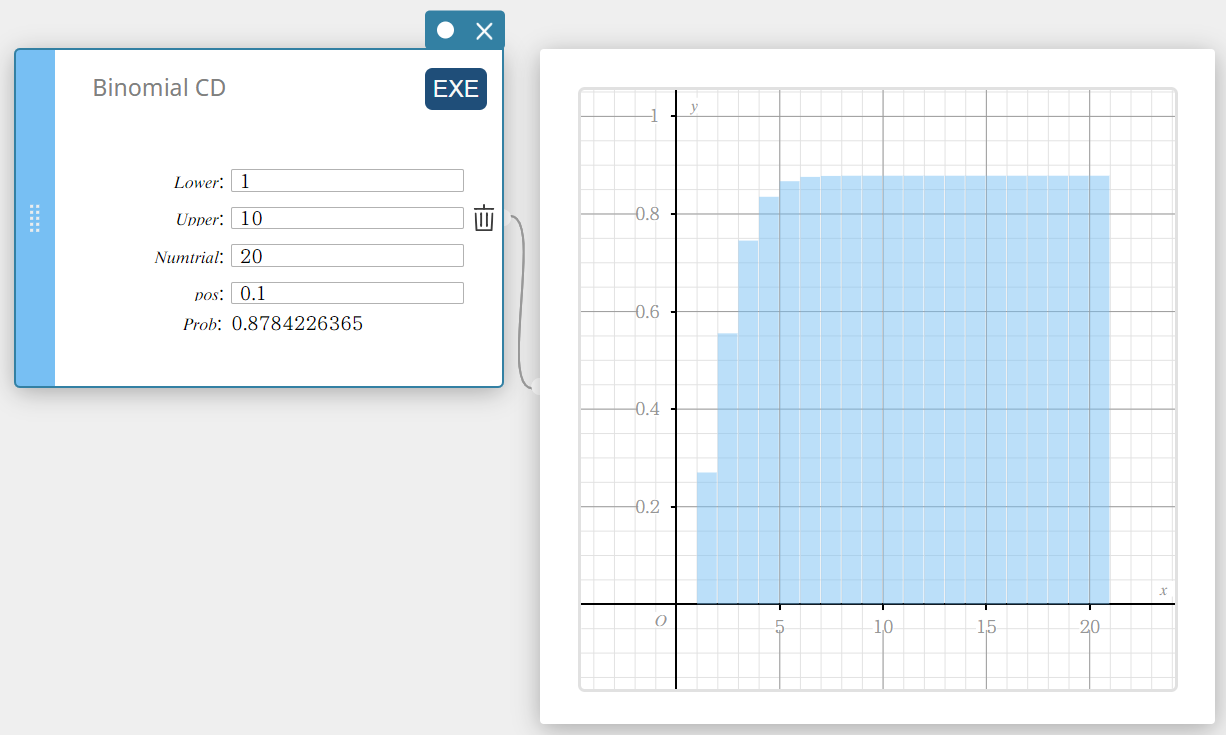
• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  Numtrial : number of trials n (integer, n \(≥\) 1)
  pos : probability of success p (0 \(≤\) p \(≤\) 1)

• Output Terms
  Prob : binomial cumulative probability

Poisson PD (Poisson Distribution Probability)
Calculates the probability in a Poisson distribution that success will occur on a specified trial.

\(f(x)=\displaystyle\frac{e^{-\lambda} \lambda^x}{x!} \qquad (x=0,1,2,\cdots)\)

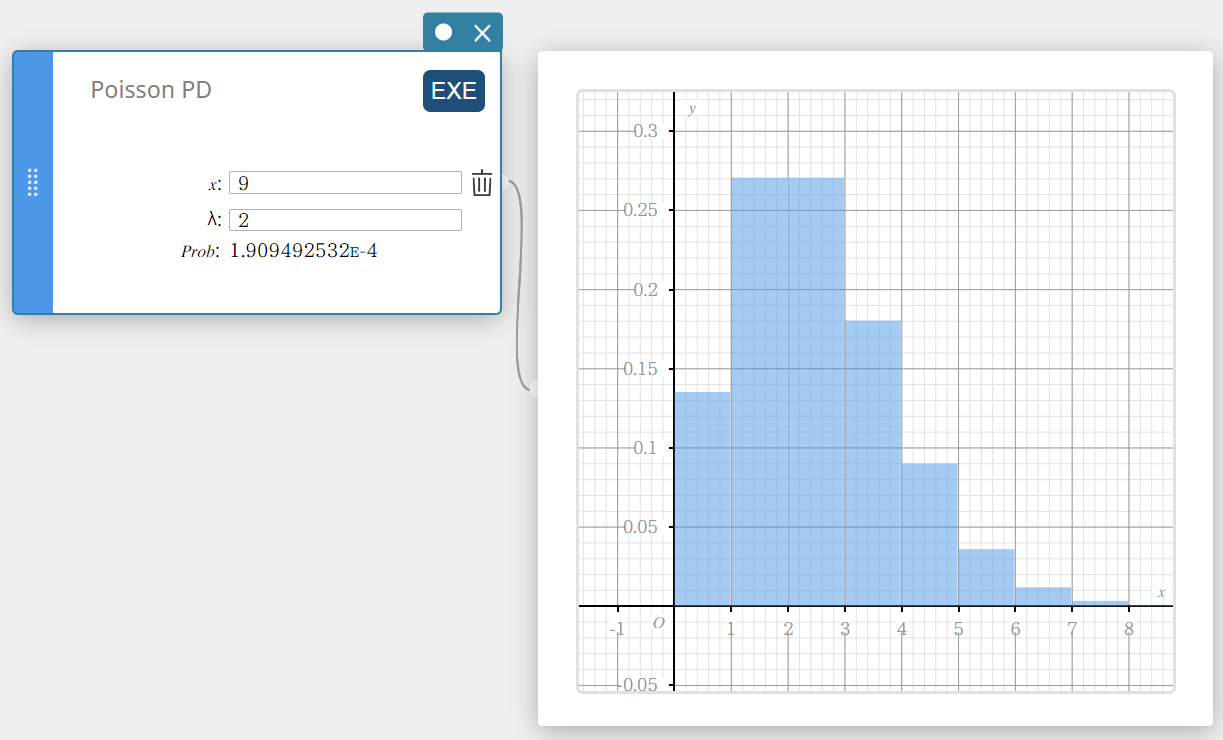
• Input Terms
  \( x \) : specified trial (integer, x \(≥\) 0)
  \( \lambda \) : mean（\(\lambda \gt 0\)）

• Output Terms
  Prob : Poisson probability

Poisson CD (Poisson Cumulative Distribution)
Calculates the cumulative probability in a Poisson distribution that success will occur on or before a specified trial.

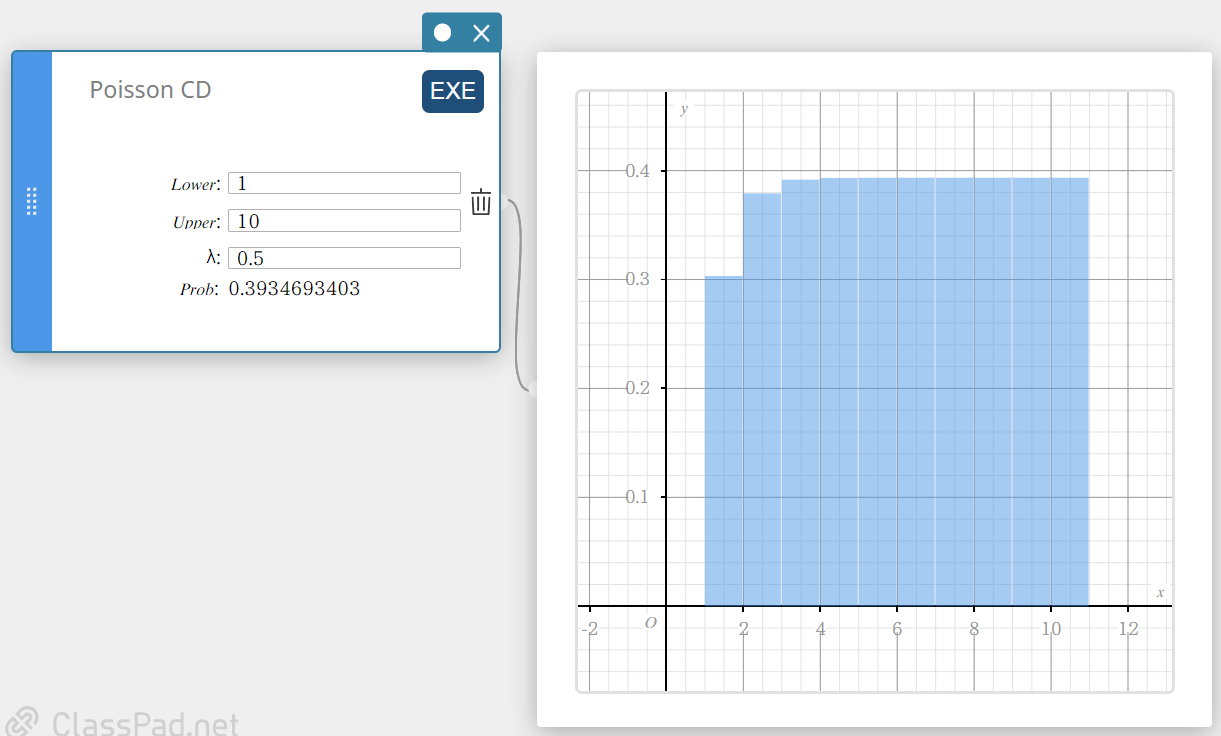
• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \( \lambda \) : mean（\(\lambda \gt 0\)）

• Output Terms
  Prob : Poisson cumulative probability

Geometric PD (Geometric Distribution Probability)
Calculates the probability in a geometric distribution that the success will occur on a specified trial.

\( f(x)=p(1-p)^{x-1} \qquad (x=1,2,3,\cdots) \)

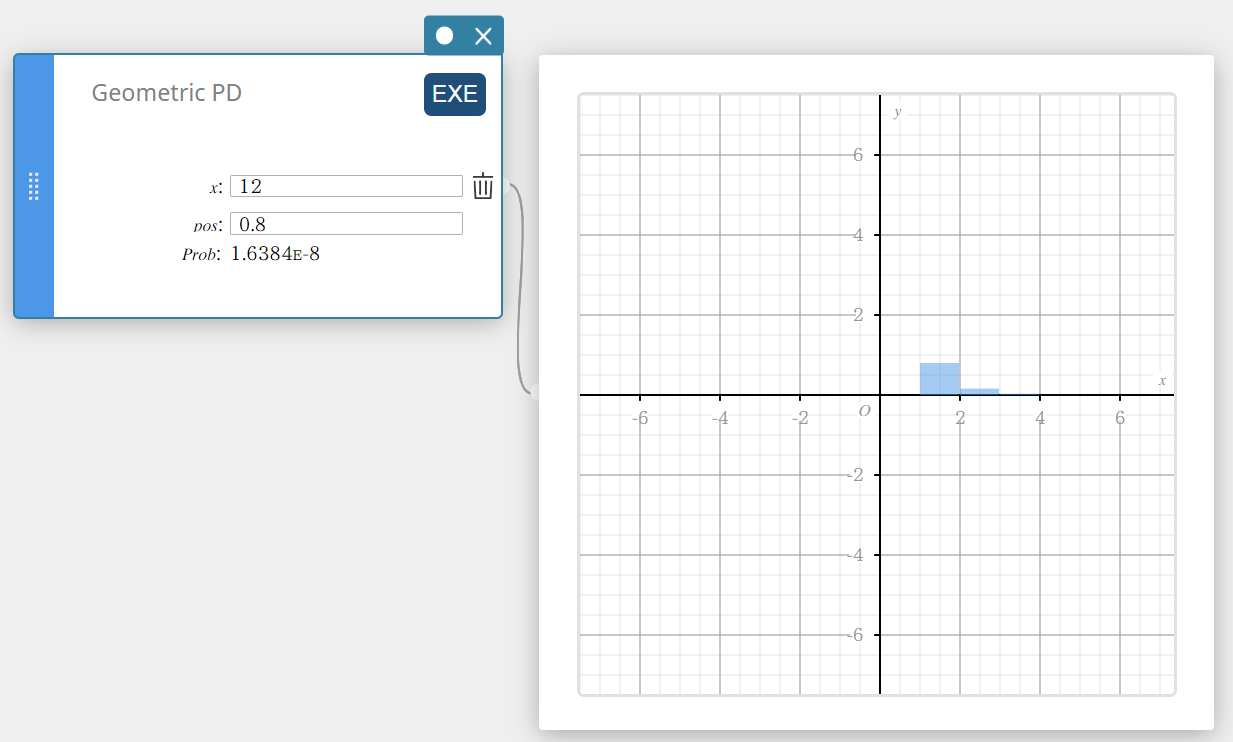
• Input Terms
  \( x \) : specified trial (positive integer)
  pos : probability of success p (0 \(≤\) p \(≤\) 1)

• Output Terms
  Prob : geometric probability

Geometric CD (Geometric Cumulative Distribution)
Calculates the cumulative probability in a geometric distribution that the success will occur on or before a specified trial.

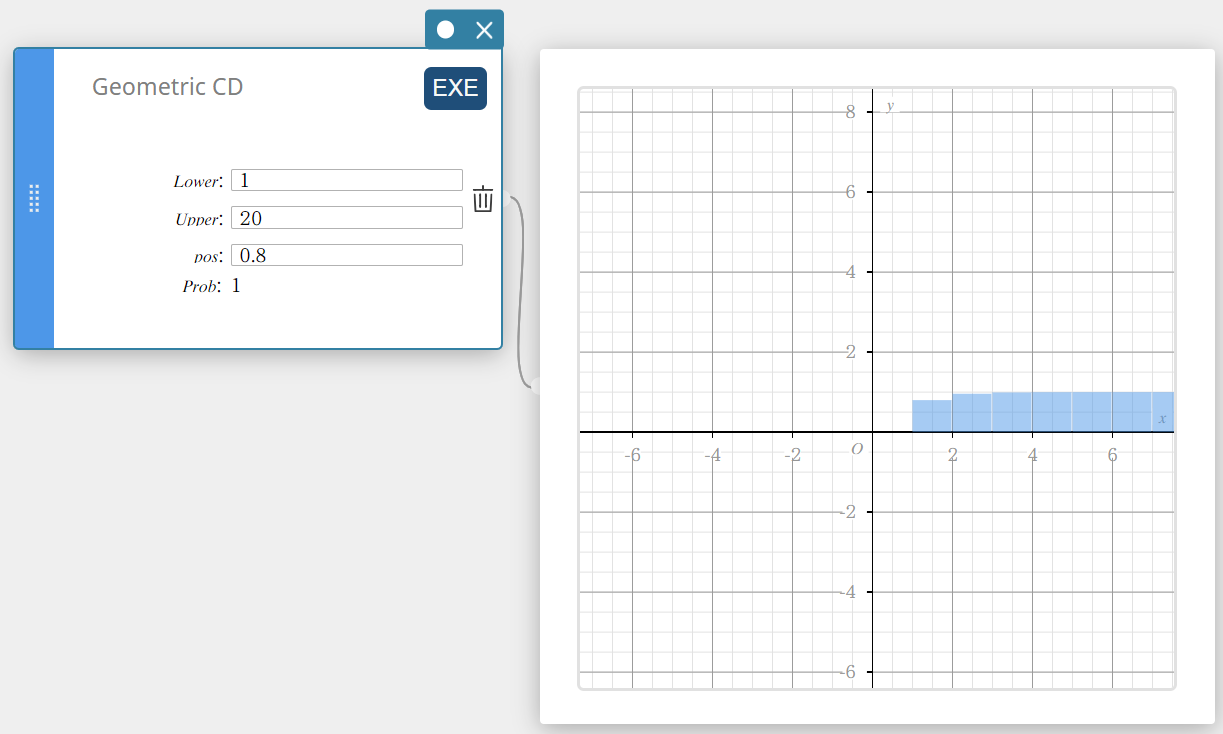
• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  pos : probability of success p (0 \(≤\) p \(≤\) 1)

• Output Terms
  Prob : geometric cumulative probability

Hypergeometric PD (Hypergeometric Distribution Probability)
Calculates the probability in a hypergeometric distribution that the success will occur on a specified trial.

\( prob = \displaystyle\frac{ {}_MC_x \times {}_{N-M}C_{n-x} }{ {}_NC_n } \)

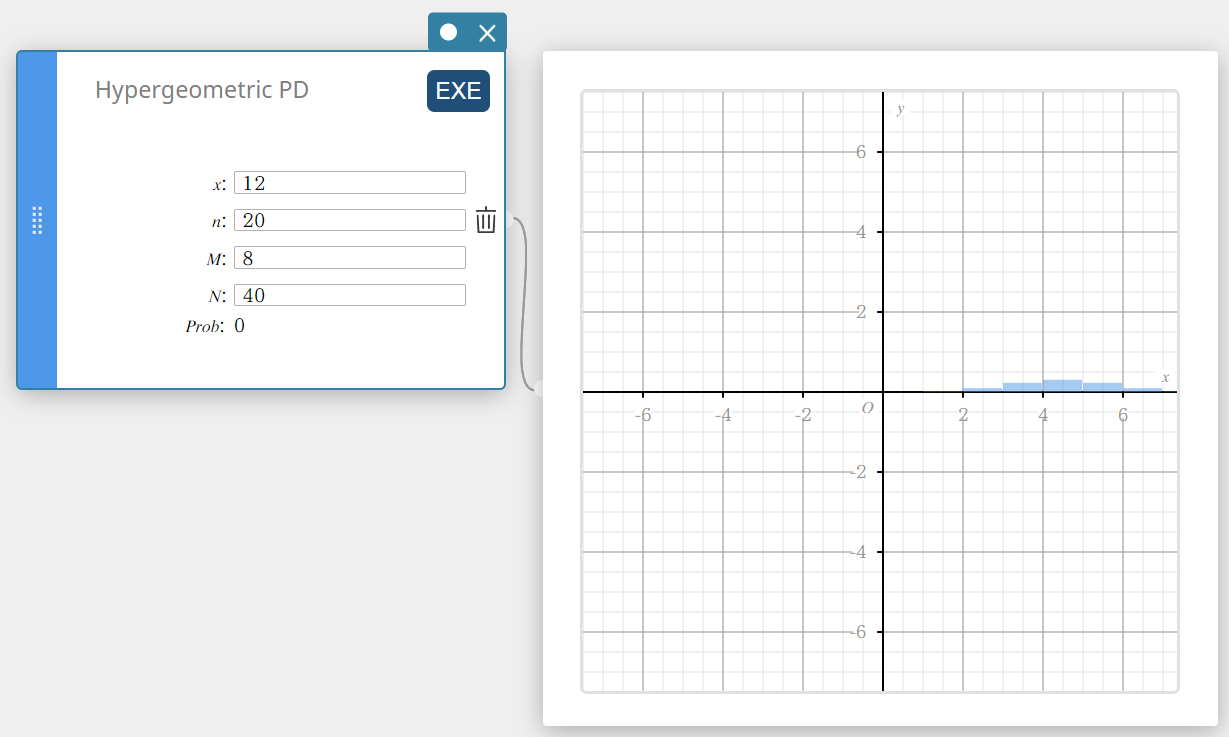
• Input Terms
  \(x\) : specified trial (integer)
  \(n\) : number of trials from population (0 \(≤\) n integer)
  \(M\) : number of successes in population (0 \(≤\) M integer)
  \(N\) : population size ( n \(≤\) N , M \(≤\) N integer)

• Output Terms
  Prob : hypergeometric probability

Hypergeometric CD (Hypergeometric Cumulative Distribution)
Calculates the cumulative probability in a hypergeometric distribution that the success will occur on or before a specified trial.

\( prob = \sum_{i=Lower}^{Upper}\displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

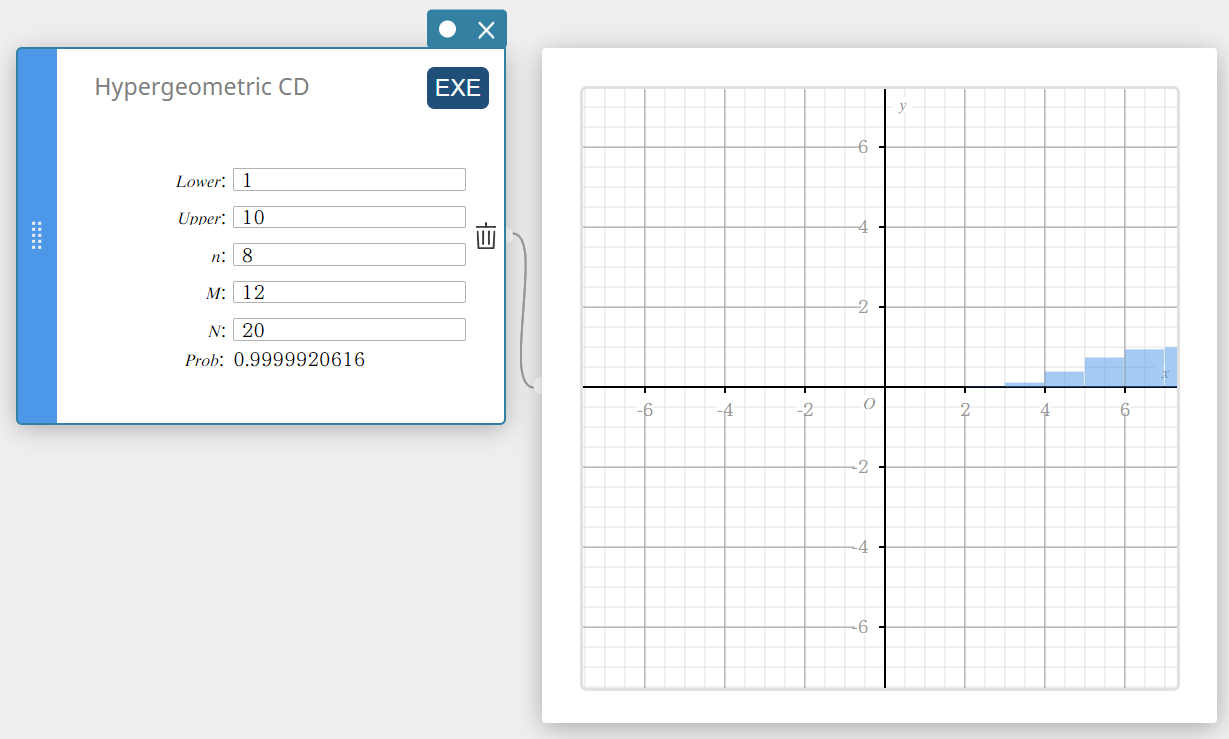
• Input Terms
  Lower : lower boundary
  Upper : upper boundary
  \(n\) : number of trials from population (0 \(≤\) n integer)
  \(M\) : number of successes in population (0 \(≤\) M integer)
  \(N\) : population size ( n \(≤\) N , M \(≤\) N integer)

• Output Terms
  Prob : hypergeometric cumulative probability

Inverse Normal CD (Inverse Normal Cumulative Distribution)
Calculates the boundary value(s) of a normal cumulative probability distribution for specified values.

Tail: Left
\( \int_{-\infty}^{\alpha}f(x)dx=p \)
Upper bound α is returned.

Tail: Right
\( \int_{\alpha}^{+\infty}f(x)dx=p \)
Lower bound α is returned.

Tail: Center
\( \int_{\alpha}^{\beta}f(x)dx=p \qquad \left( \mu=\displaystyle\frac{\alpha+\beta}{2} \right) \)
Lower bound α and upper bound β are returned.

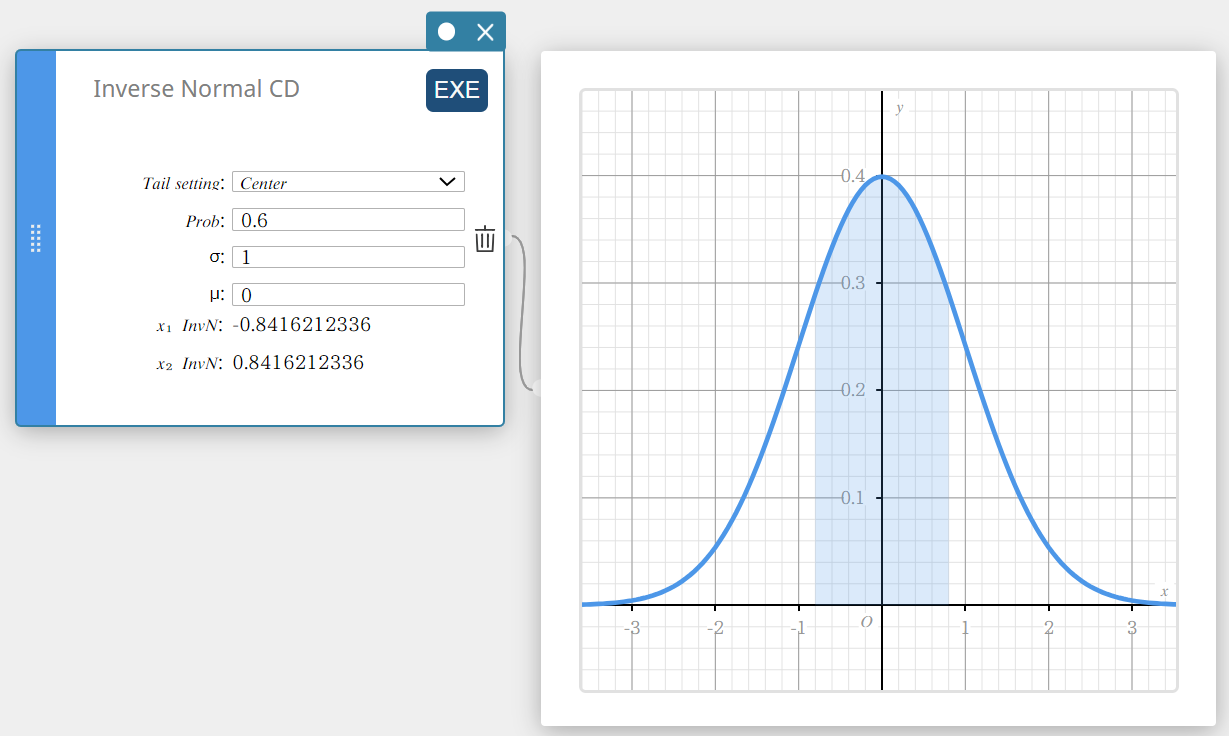
• Input Terms
  Tail setting: probability value tail specification (Center, Left, Right)
  Prob : probability value (0 \(≤\) Area \(≤\) 1)
  \( \sigma \) : population standard deviation（\( \sigma > 0 \)）
  \( \mu \) : population mean

• Output Terms
  \(x_1 {\rm InvN}\) : Upper bound when Tail: Left
       Lower bound when Tail: Right or Tail:Center
  \(x_2 {\rm InvN}\) : Upper bound when Tail: Center

Inverse t CD (Inverse Student’s t Cumulative Distribution)
Calculates the lower bound value of a Student’s t cumulative probability distribution for specified values.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Input Terms
  Prob : t cumulative probability (0 \(≤\) Area \(≤\) 1)
  \(df\) : degrees of freedom (df > 0)

• Output Terms
  xInv: The lower bound value of a Student’s t cumulative probability distribution

Inverse \(\chi^2\) CD (Inverse \(\chi^2\) Cumulative Distribution)

Calculates the lower bound value of a \(\chi^2\) cumulative probability distribution for specified values.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Input Terms
  Prob : \(\chi^2\) cumulative probability (0 \(≤\) Area \(≤\) 1)
  \(df\) : degrees of freedom (positive integer)

• Output Terms
  \(x {\rm Inv}\) : The lower bound value of a \(\chi^2\) cumulative probability distribution

Inverse F CD (Inverse F Cumulative Distribution)
Calculates the lower bound value of an F cumulative probability distribution for specified values.

\( \int_{\alpha}^{+\infty}f(x)=p \)

• Input Terms
  Prob : F cumulative probability (0 \(≤\) Area \(≤\) 1)
  \(n:df\) : degrees of freedom of numerator (positive integer)
  \(d:df\) : degrees of freedom of denominator (positive integer)

• Output Terms
  xInv: The lower bound value of an F cumulative probability distribution

Inverse Binomial CD (Inverse Binomial Cumulative Distribution)
Calculates the minimum number of trials of a binomial cumulative probability distribution for specified values.

\( \sum_{x=0}^{m}f(x)\ge prob \)

• Input Terms
  Prob : binomial cumulative probability（\(0 \le\) Area \(\le 1\)）
  Numtrial : number of trials n (integer, n \(≥\) 0)
  pos : probability of success p (0 \(≤\) p \(≤\) 1)

• Output Terms
  xInv : The lower bound value of an F cumulative probability distribution

Inverse Poisson CD (Inverse Poisson Cumulative Distribution)
Calculates the minimum number of trials of a Poisson cumulative probability distribution for specified values.

\( \sum_{x=0}^{m}f(x)\ge prob \)

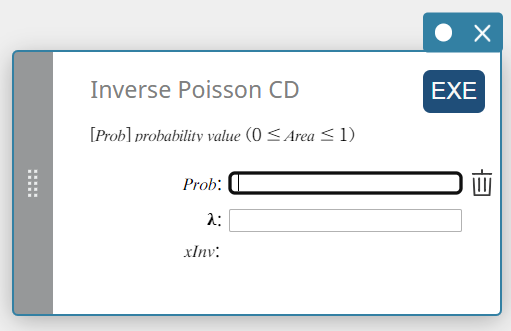
• Input Terms
  Prob : Poisson cumulative probability（\(0 \le\) Area \(\le 1\)）
  \( \lambda \) : mean（\(\lambda \gt 0\)）

• Output Terms
  xInv : The minimum number of trials (the upper bound value) of a Poisson cumulative probability distribution

Inverse Geo CD (Inverse Geometric Cumulative Distribution)
Calculates the minimum number of trials of a geometric cumulative probability distribution for specified values.

\( \sum_{x=0}^{m}f(x)\ge prob \)

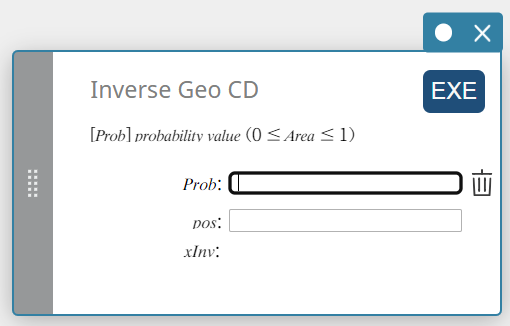
• Input Terms
  Prob : geometric cumulative probability（\(0 \le\) Area \(\le 1\)）
  pos : probability of success p（\(0 \le p \le 1\)）

• Output Terms
  xInv : The minimum number of trials (the upper bound value) of a geometric cumulative probability distribution

Inverse Hypergeometric (Inverse Hypergeometric Cumulative Distribution)
Calculates the minimum number of trials of a hypergeometric cumulative probability distribution for specified values.

\( prob \le \sum_{i=0}^{X} \displaystyle\frac{ {}_MC_i \times {}_{N-M}C_{n-i} }{ {}_NC_n } \)

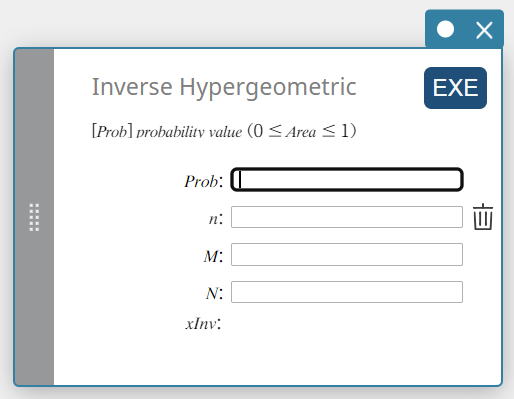
• Input Terms
  Prob : hypergeometric cumulative probability（\(0 \le\) Area \(\le 1\)）
  \(n\) : number of trials from population (0 \(≤\) n integer)
  \(M\) : number of successes in population (0 \(≤\) M integer)
  \(N\) : population size ( n \(≤\) N , M \(≤\) N integer)

• Output Terms
  xInv: The minimum number of trials (the upper bound value) of a hypergeometric cumulative probability distribution

Other Statistical Graphs

Scatter Plot
This plot compares the data accumulated ratio with a normal distribution accumulated ratio. If the scatter plot is close to a straight line, then the data is approximately normal. A departure from the straight line indicates a departure from normality.

Box & Whisker Plot
This type of graph lets you see how a large number of data items are grouped within specific ranges. A box encloses all the data in an area from the first quartile (\({\rm Q}_1\)) to the third quartile (\({\rm Q}_3\)), with a line drawn at the median (\({\rm Med}\)). Lines (called whiskers) extend from either end of the box up to the minimum (\({\rm minX}\)) and maximum (\({\rm maxX}\)) of the data.

Histogram
A histogram shows the frequency (frequency distribution) of each data class as a rectangular bar. Classes are on the horizontal axis, while frequency is on the vertical axis. If necessary, you can change the start value (\(HStart\)) and step value (\(HStep\)) of the histogram.

Pie Chart
You can draw a circle graph based on the data in a specific list.

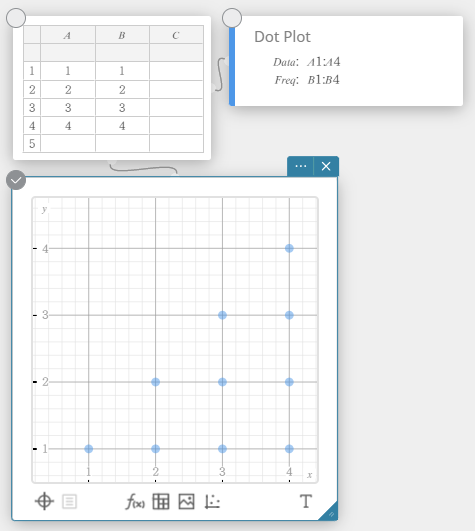
Dot Plot
The values in Column A (horizontal axis) represent bin numbers, while the values in Column B (vertical axis) represent the data point count in each bin. A dot is plotted for each data point in a bin.