Arithmetic and Function Calculations

table of contents

Performing an Arithmetic Calculation
Entering Functions
Software Keyboard
List Calculations
Matrix and Vector Calculations
Copying a Formula
Auto-completion
Complex Number Calculations
Using Answer Memory (ans)
Using Variables
Using Variable Manager
Using the Interactive Menu
Inserting Subscript
Configuring Calculation Settings

Performing an Arithmetic Calculation

1. Click in the sticky note menu.
   
   This creates a Math sticky note and displays the software keyboard.
   
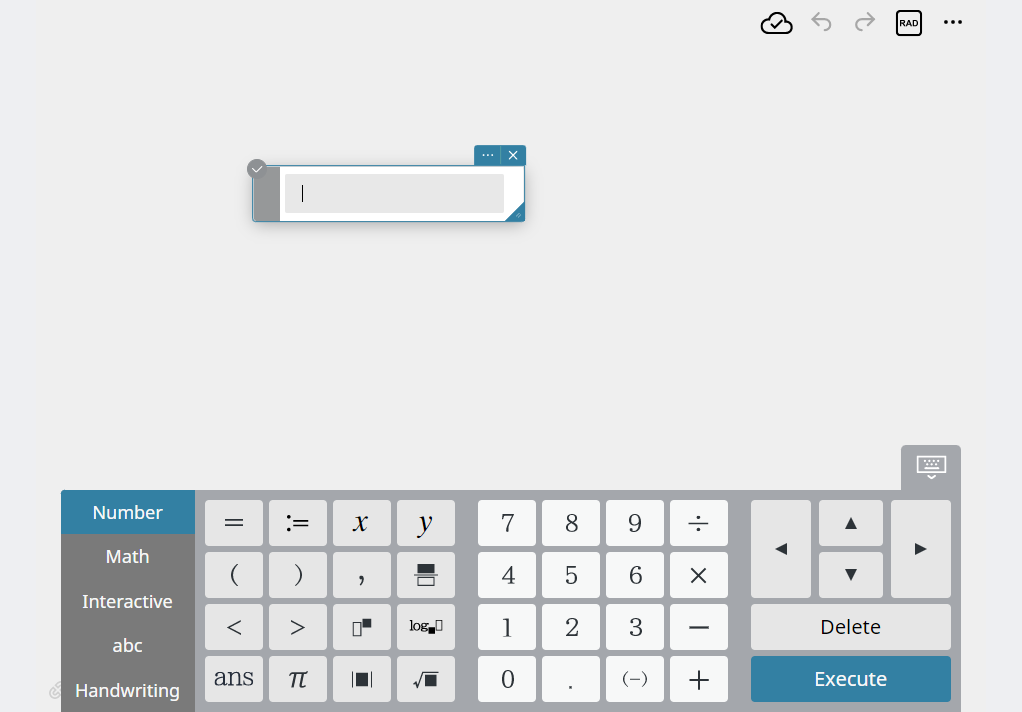
2. Use the software keyboard to enter a calculation expression.
   Example: \(4 \div 5 + 2 \div 3\)
   Keyboard operation: \([4][\div][5][\blacktriangleright][+][2][\div][3]\)
   
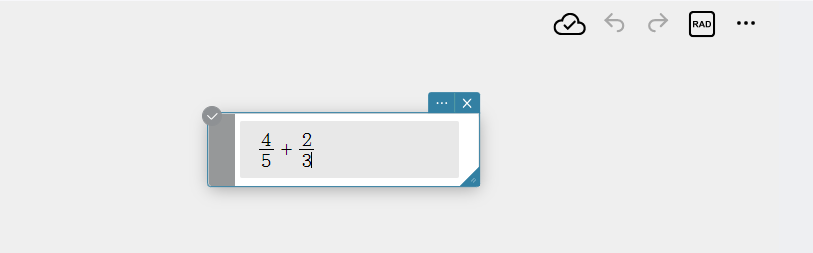
3. On the software keyboard, click [Execute].
   The calculation result of the expression you enter appears below the expression, aligned with the right margin.
   
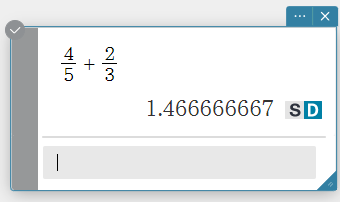
   You can proceed with other calculations from here by repeating steps 2 and 3 of this procedure.
   

MEMO
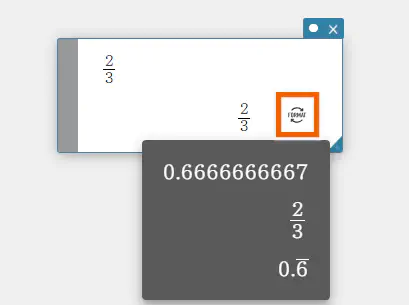
Selecting displayed to the right of the calculation result changes the display form of the calculation result.
You can choose a display form from the followings:
Fraction (including formulas using √ or π), decimal, repeating decimal、rectangular coordinates、polar coordinates、mixed number.
The order of forms displayed right after the calculation depends on the setting of “Calculation Results” (see “Configuring Calculation Settings“).

If the calculation results are longer than the window width, the scroll bar will be displayed.Move the scroll bar horizontally to see whole calculation results.

Entering Functions

1. Click 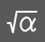in the sticky note menu.
   
   This creates a Math sticky note and displays the software keyboard.
   
2. On the software keyboard, click the [Math] tab.
   This displays the Math keyboard.
   
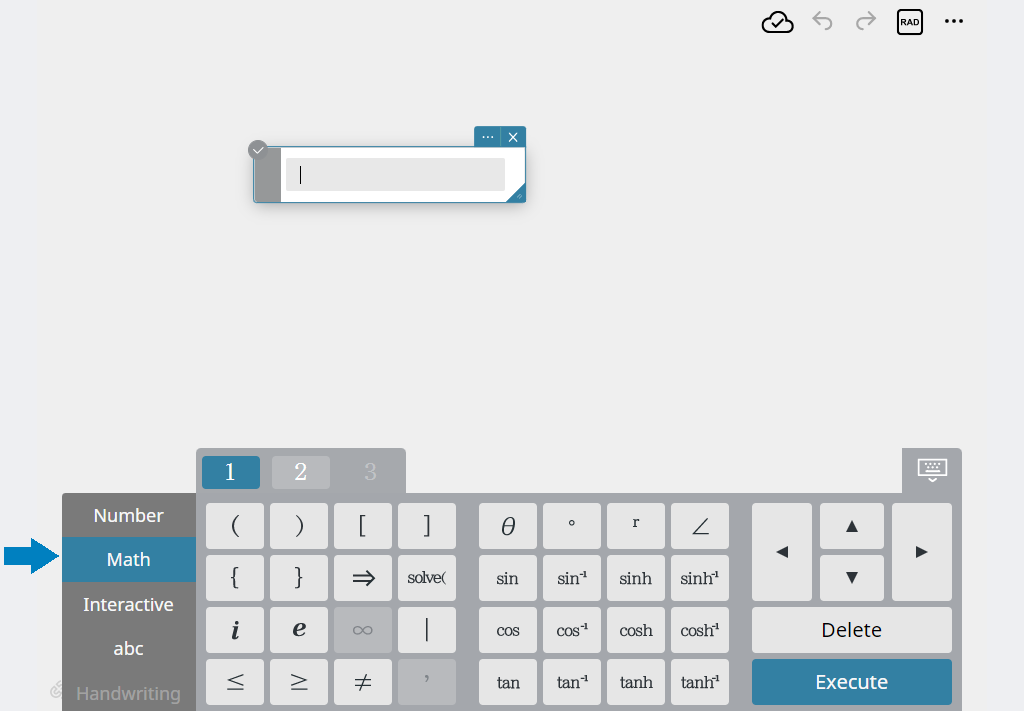
3. Click the function you want to enter.
   
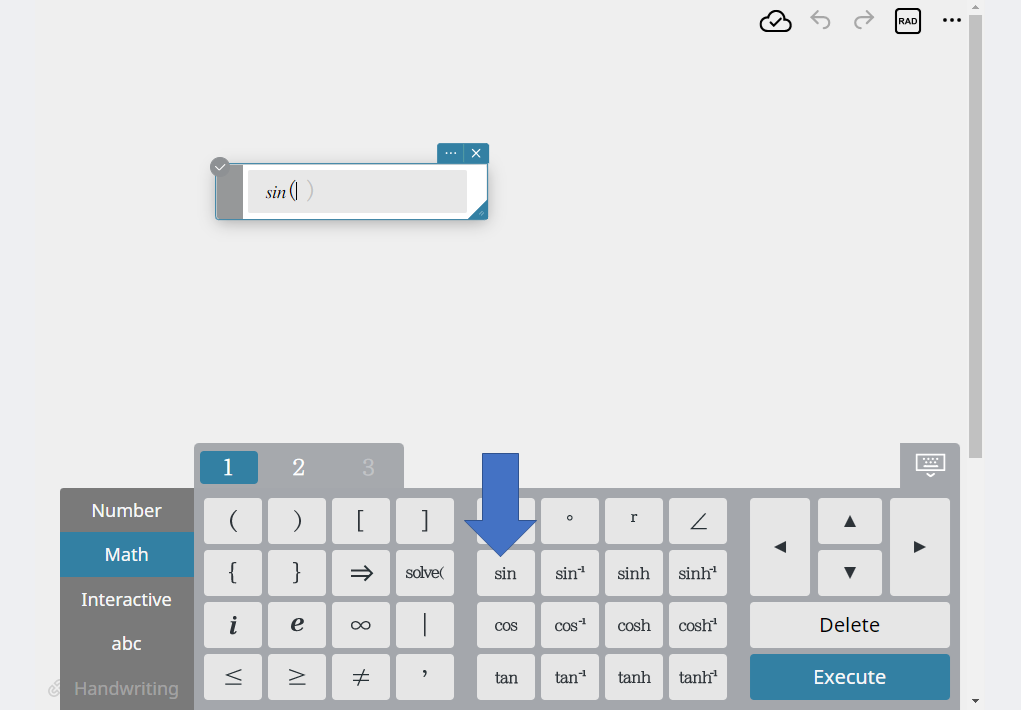
   Clicking or on the Math keyboard changes the Function key display.
   
   MEMO
   You can also use the alphabetic keyboard to enter functions.

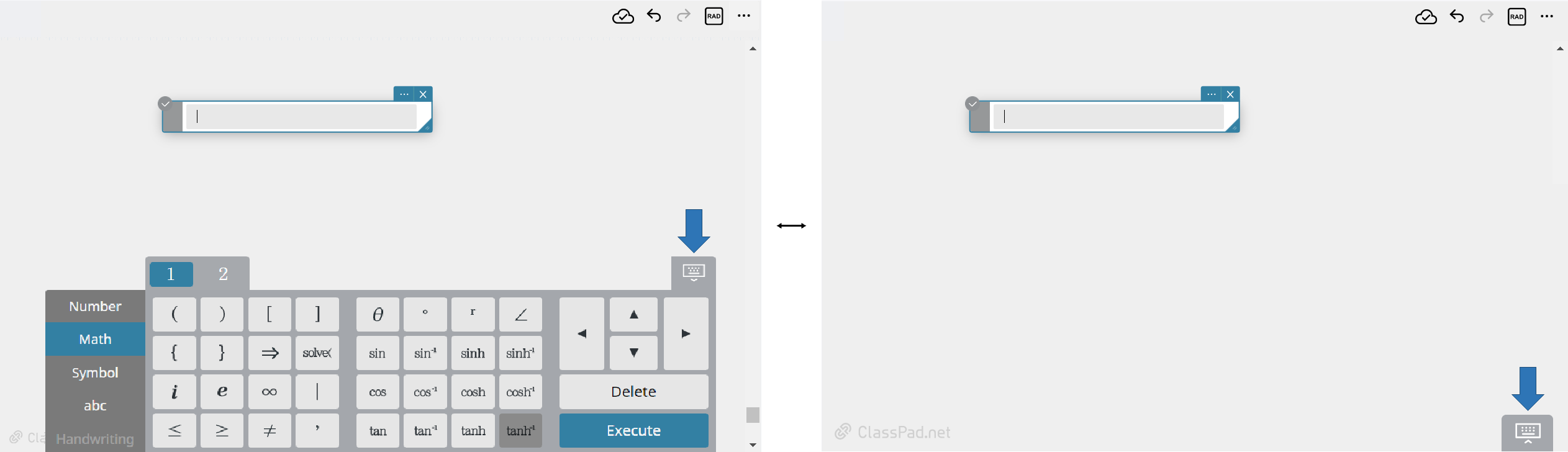
Software Keyboard

A software keyboard is displayed below the Paper for entering calculation expressions and functions.
The available software keyboards are shown below.

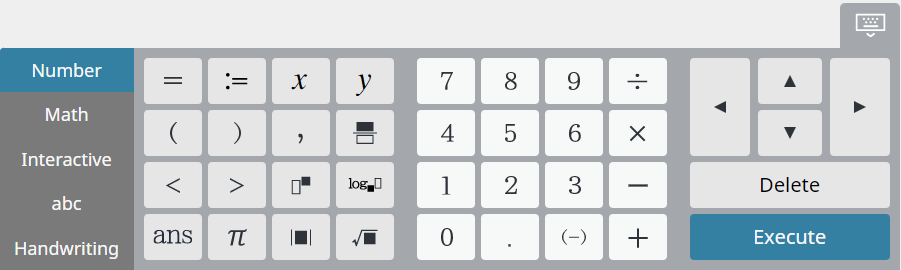
Numeric keyboard
Use this keyboard to enter numbers, arithmetic operators, and the most basic symbols required for writing formulas.

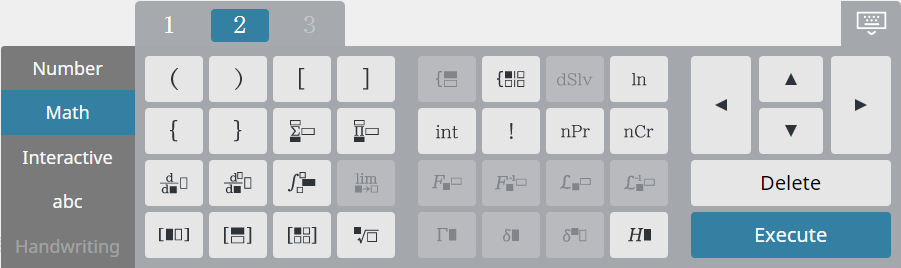
Math keyboard
Use this keyboard to enter trigonometric and other functions. Click [1], [2], or [3] to navigate between keyboard types.

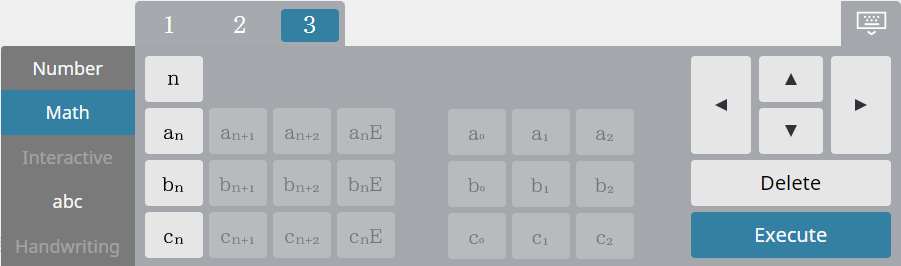
MEMO
[3] is a keyboard used for sequence calculations (see “Sequence”). It can only be used for Sequence sticky notes.

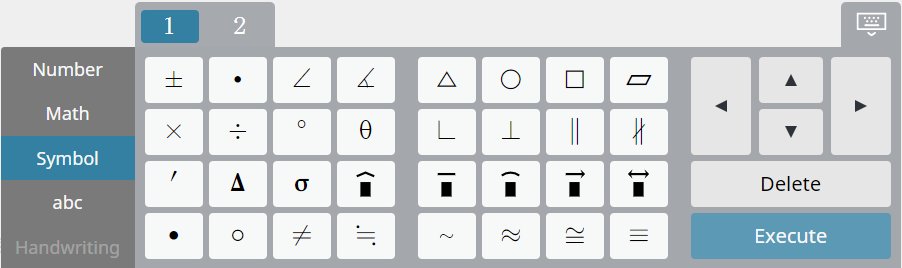
[Symbol] keyboard (Text sticky note only)
Use this keyboard to enter special calculation formats or symbols that use subjects other than math.

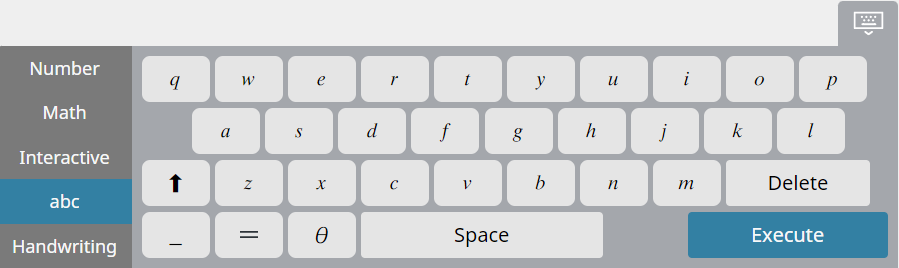
Alphabetic keyboard
Use this keyboard to enter alphabetic characters for variables, etc.

Geometry or Text sticky notes

Handwriting panel
This handwriting panel can be used to input calculation expressions and functions by writing them.

MEMO
To hide the software keyboard, click . To re-display the keyboard, click .

List Calculations

Values enclosed in braces ({ }) are considered to be a list. The values in a list are separated by commas (,).

• To store a list in a variable

Example: To store {\(1,2,3\)} in variable “lista”.

1. Create a Math sticky note.
2. Enter the following: {\(1,2,3\)} ⇒lista.
   Use the [Math] keyboard to enter “⇒”.
   
3. On the software keyboard, click [Execute].
   
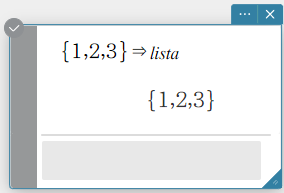
   This stores the list {\(1,2,3\)} in variable “lista”.

• To recall a particular element of a list

Example: To recall the second element of the list stored in variable “lista”({\(1,2,3\)})

1. Enter the following: lista[2].
   The values entered in the brackets ([ ]) are numbers (index numbers) of the elements you are recalling.
2. On the software keyboard, click [Execute].
   
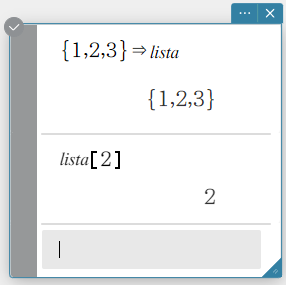
   This recalls the second element (\(2\)) of the list stored in variable “lista”.

• To store a value in an element of a list

Example: To substitute \(5\) for the second element of the list stored in variable “lista”

1. Enter the following: \(5\)⇒lista[2].
2. On the software keyboard, click [Execute].
   
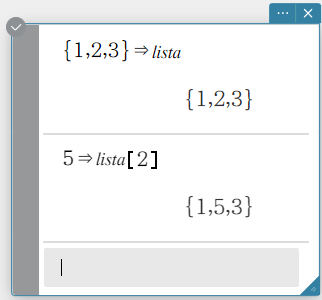
   This substitutes \(5\) for the second element of the list stored in variable “lista”.

• To perform list calculations
  You can perform arithmetic operations between two lists, between a list and a numeric value, or between a list and an expression, equation, or inequality.

Important
When you perform an arithmetic operation between two lists, both of the lists need to have the same number of elements.
An error will occur if they do not.
An error will also occur whenever an operation between any two elements of the two lists results in an error.
Example: Execute list3({\(41,65,22\)}) \(\times\){\(6,0,4\)}
① Enter the following: {\(41,65,22\)}⇒list3.
② On the software keyboard, click [Execute].
③ Enter the following: list3 \(\times\) {\(6,0,4\)}.
④ On the software keyboard, click [Execute].

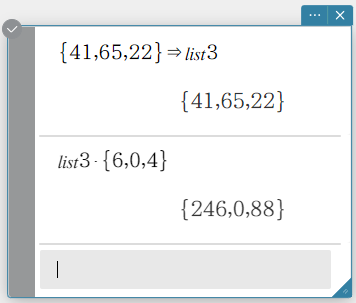
This displays the results of the list calculation.

MEMO
To check the variable in which the list is stored, click >[Variable Manager] in the Paper header. For details, see “Using Variable Manager”.

Matrix and Vector Calculations

You can enter a matrix or vector using single line syntax, or actual form syntax. A vector is regarded as 1-row x n-column or n-row x 1-column matrix, so a separate explanation of vectors will not be provided here.

• To store a matrix in a variable

Example: To store the matrix \(\left[\begin{array}{ccc} 1 & 2 \cr 3 & 4 \end{array}\right]\) in variable “mat1”

1. Create a Math sticky note.
2. Enter the following: \([[1,2][3,4]]\) ⇒mat1
3. On the software keyboard, click [Execute].
   
   This stores matrix \([[1,2][3,4]]\) in variable “mat1”.

• To recall specific elements of a matrix

Example: To recall the element at row 2, column 1 of the matrix stored in variable “mat1” \(\left( \left[\begin{array}{ccc} 1 & 2 \cr 3 & 4 \end{array}\right] \right)\)

1. Enter the following: mat1[2,1].
   The values entered in the brackets ([ ]) are the rows and columns of the elements you are recalling.
   Enter values into the brackets ([ ]) in the following sequence [row number, column number].
2. On the software keyboard, click [Execute].
   
   This recalls the element at row 2, column 1 (3) of the matrix stored in variable “mat1”.

• To enter a value into a matrix element

Example: To substitute \(5\) for the element at row 1, column 2 of the matrix stored in variable “mat1” \(\left( \left[\begin{array}{ccc} 1 & 2 \cr 3 & 4 \end{array}\right] \right)\)

1. Enter the following: \(5\)⇒mat1[1,2].
2. On the software keyboard, click [Execute].
   
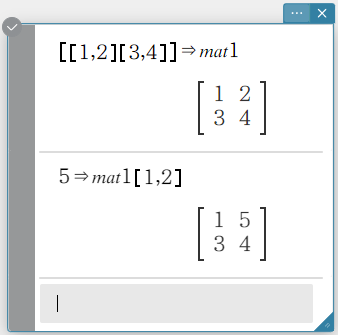
   This substitutes \(5\) for the element at row 1, column 2 of the matrix stored in variable “mat1”.

• To use the Math keyboard to enter a matrix using actual form syntax
  Click one of the keys below to enter the matrix.

1. To enter a 1-row x 2-column matrix
2. To enter a 2-row x 1-column matrix
3. To enter a 2-row x 2-column matrix
4. To add a column to the currently displayed matrix
5. To add a row to the currently displayed matrix
6. To add both a row and column to the currently displayed matrix

Example: To store the matrix \(\left[\begin{array}{ccc} 1 & 2 & 3 \cr 4 & 5 & 6 \end{array}\right]\) in variable “mat2”

1. On the Math keyboard, click .
2. On the Numeric keyboard, click \([1][\blacktriangleright][2]\).
3. On the Math keyboard, click .
4. On the Numeric keyboard, click [3].
5. On the Math keyboard, click .
6. Click the column 1 in row 2 of the matrix.
7. On the Numeric keyboard, click \([4][\blacktriangleright][5][\blacktriangleright][6][\blacktriangleright]\).
8. Enter the following: ⇒mat2.
9. On the software keyboard, click [Execute].
   
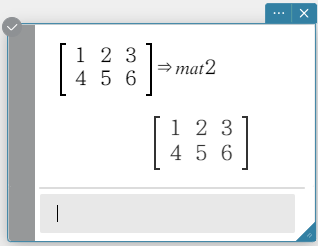
   This stores the matrix \(\left[\begin{array}{ccc} 1 & 2 & 3 \cr 4 & 5 & 6 \end{array}\right]\) in variable “mat2”.

• To perform matrix arithmetic

Example 1: To perform the calculation \(\left[\begin{array}{ccc} 1 & 1 \cr 2 & 1 \end{array}\right] + \left[\begin{array}{ccc} 2 & 3 \cr 2 & 1 \end{array}\right]\)

1. Enter the following: \([[1,1][2,1]]+[[2,3][2,1]]\).
2. On the software keyboard, click [Execute].
   
   This displays the results of the Matrix calculation.

Example 2: To use the Math keyboard to perform the calculation \(\left[\begin{array}{ccc} 1 & 1 \cr 2 & 1 \end{array}\right] \times \left[\begin{array}{ccc} 2 & 3 \cr 2 & 1 \end{array}\right]\)

1. On the Math keyboard, click .
2. On the Numeric keyboard, click
   \([1][\blacktriangleright][1][\blacktriangledown][\blacktriangleleft][2][\blacktriangleright][1][\blacktriangleright][×]\).
3. On the Math keyboard, click .
4. On the Numeric keyboard, click
   \([2][\blacktriangleright][3][\blacktriangledown][\blacktriangleleft][2][\blacktriangleright][1]\).
5. On the software keyboard, click [Execute].
   

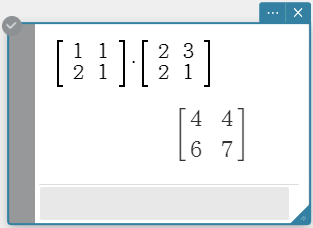
Example 3: To multiply \(\left[\begin{array}{ccc} 1 & 2 \cr 3 & 4 \end{array}\right]\) by 5

1. Enter the following: [[1,2][3,4]]×5.
2. On the software keyboard, click [Execute].
   

Example 4: To cube \(\left[\begin{array}{ccc} 1 & 1 \cr 3 & 4 \end{array}\right]\)

1. On the Math keyboard, click .
2. On the Numeric keyboard, click
   \([1][\blacktriangleright][1][\blacktriangledown][\blacktriangleleft][3][\blacktriangleright][4][\blacktriangleright][{\tiny{ \boxed{ \vphantom{0} \hspace{0.1em} } } } ^ {\tiny{\blacksquare}}][3]\).
3. On the software keyboard, click [Execute].
   
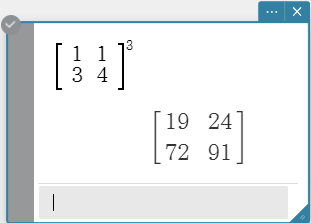
   MEMO
   To check the variable in which the matrix is stored, click >[Variable Manager] in the Paper header. For details, see “Using Variable Manager”.

Copying a Formula

• To select a numeric expression and copy it

1. Drag the mouse pointer across the expression you want to copy to select it.
   
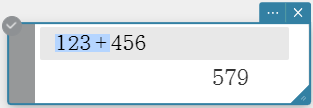
2. On your computer keyboard, press [Ctrl]+[C].
3. Click the location where you want to paste the formula.
   
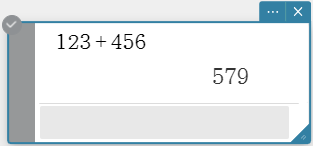
4. On your computer keyboard, press [Ctrl]+[V].
   This pastes the copied formula.
   
   MEMO
   A copied formula can also be pasted into another sticky note.
   You can also select a formula and copy it using drag-and-drop.
   You can also paste by right-clicking to display the context menu and then selecting [Paste].

• To copy an entire numeric expression

1. Click within the numeric expressions you want to copy.
   
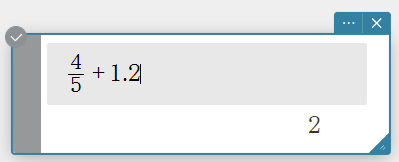
2. Right-click to display the context menu and then select [Copy Line].
   
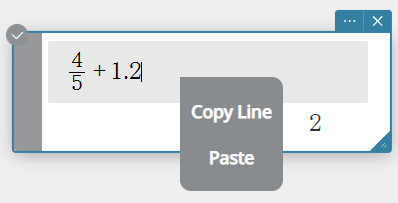
3. Click the location where you want to paste the expression.
4. Right-click to display the context menu and then select [Paste].
   
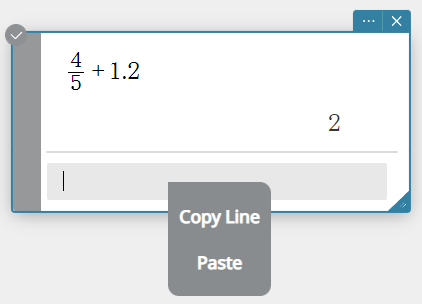
   This pastes the copied expression.
   
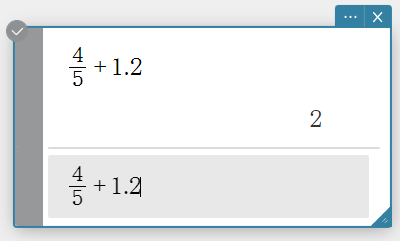
   You can also paste by pressing [Ctrl]+[V] on your computer keyboard.
   

MEMO
If you are using a tablet, you can display the context menu using a long-tap operation.

Auto-completion

Auto-completion is a function that displays a list of functions that match part of a text string you have entered. While you are entering text, the list updates sequentially each time you enter another character. You can select a function shown in the list, making it quicker and simpler to enter functions.

Example: To enter “approx”

1. Display the alphabetic keyboard.
   
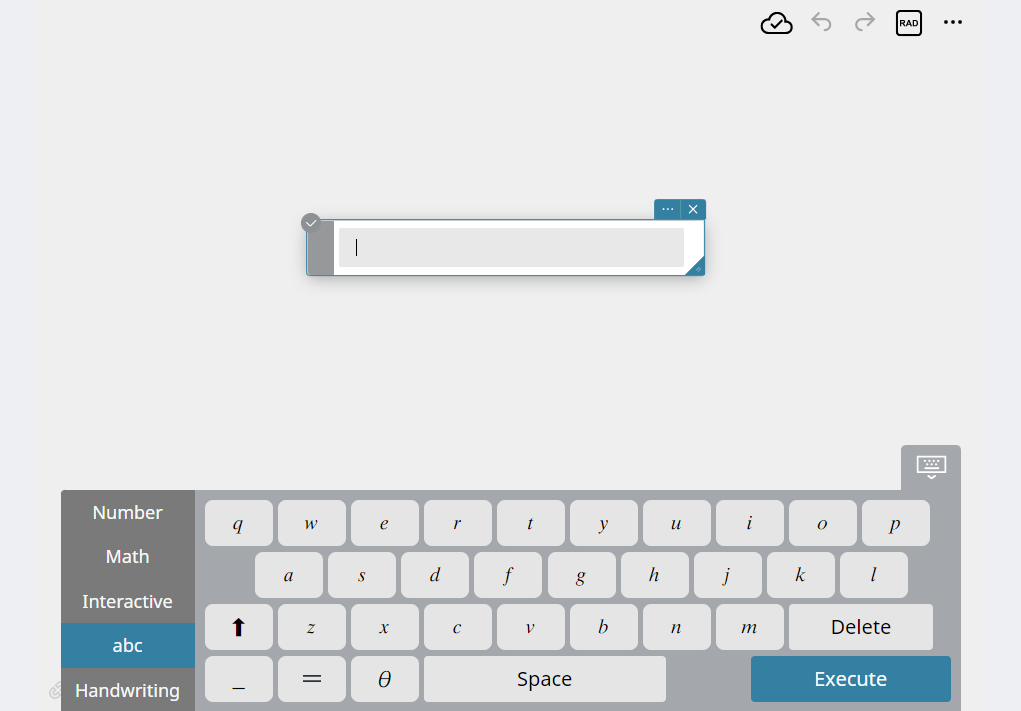
2. Enter “ap”.
   This displays a list of functions that contain the text string you entered.
   
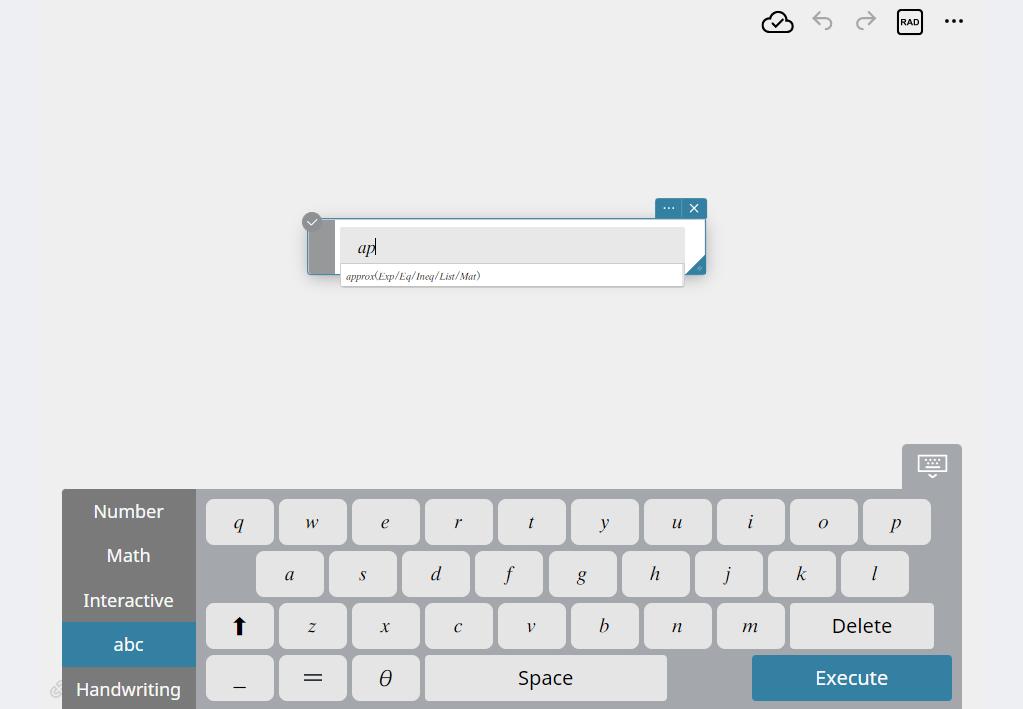
3. From the list, select “approx”.
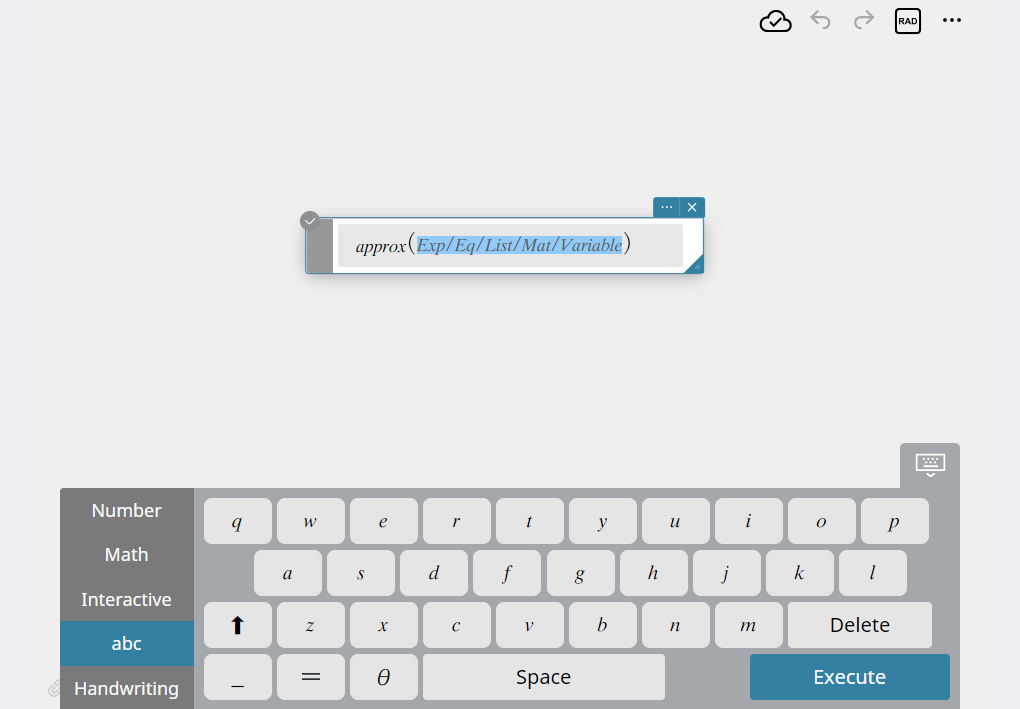
   This will enter the function you selected.
   

Complex Number Calculations

Enabling the “Complex number calculation” option in the Settings dialog box for the Math function allows you to perform arithmetic calculations that use complex numbers, calculations that use brackets and function calculations in the same way as for real numbers.
For more information on the settings for complex number calculations, see “Configuring Calculation Settings”.

Example 1: To calculate \((1+2i) + (2+3i)\)

1. Click in the Paper header.
2. Click [Math Settings] to display the Math Settings dialog box.
3. Select [On] for the [Complex Format] setting.
4. Click [OK].
5. Create a Math sticky note.
6. Enter the following: \((1+2i) + (2+3i)\).
   Use the [Math] keyboard to enter the complex number “i”.
   
7. On the software keyboard, click [Execute].
   
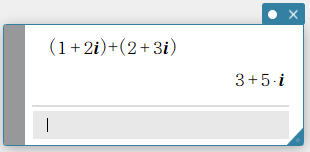
   This displays a calculation result that includes a complex number.

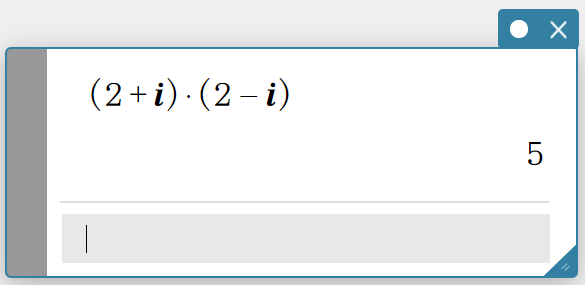
Example 2: To calculate \((2+i) \times (2-i)\)

1. Perform steps 1 through 4 under “Example 1” to select [On] for the [Complex Format] setting.
2. Create a Math sticky note.
3. Enter the following: \((2+i) \times (2-i)\).
4. On the software keyboard, click [Execute].
   

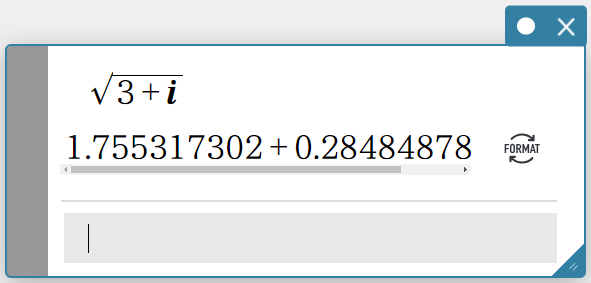
Example 3: To calculate \(\sqrt{(3+i)}\) (Calculation Results: Decimal)

1. Perform steps 1 through 4 under “Example 1” to select [On] for the [Complex Format] setting.
2. Create a Math sticky note.
3. Enter the following: \(\sqrt{(3+i)}\).
4. On the software keyboard, click [Execute].
   

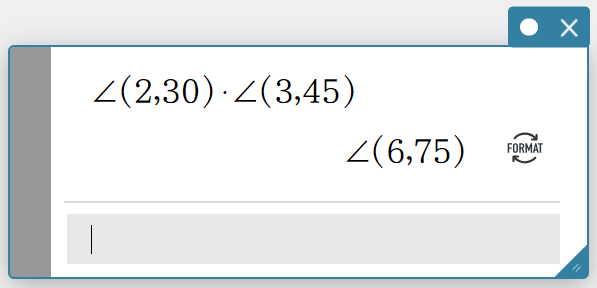
Example 4: To calculate \(2∠30 \times 3∠45\) (Angle: Degree; calculation results: Decimal)

1. Click in the Paper header.
2. Click [Math Settings] to display the Math Settings dialog box.
3. Select [On] for the [Complex Format] setting.
4. On the [Angle] pull down menu, select [Degree].
5. Click [OK].
6. Create a Math sticky note.
7. Enter the following: \(∠(2, 30) \times ∠(3, 45)\).
   Use the [Math] keyboard to enter \(∠\).
   
8. On the software keyboard, click [Execute].
   

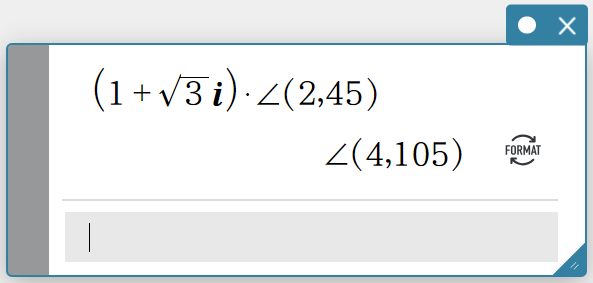
Example 5: To calculate \((1+\sqrt3 i) \times (2∠45)\) (Angle: Degree; calculation results: Decimal)

1. Perform steps 1 through 5 under “Example 4” to select [On] for the [Complex Format] setting and [Degree] for the [Angle] setting.
2. Create a Math sticky note.
3. Enter the following: \((1+\sqrt3 i) \times ∠(2, 45)\).
4. On the software keyboard, click [Execute].
   

Example 6: To calculate \({\rm solve}(x^3-x^2+x-1=0,x)\)

1. Perform steps 1 through 4 under “Example 1” to select [On] for the [Complex Format] setting.
2. Create a Math sticky note.
3. Enter the following: \({\rm solve}(x^3-x^2+x-1=0,x)\).
   Use the [Math] keyboard to enter \({\rm solve}(\).
   
4. On the software keyboard, click [Execute].
   

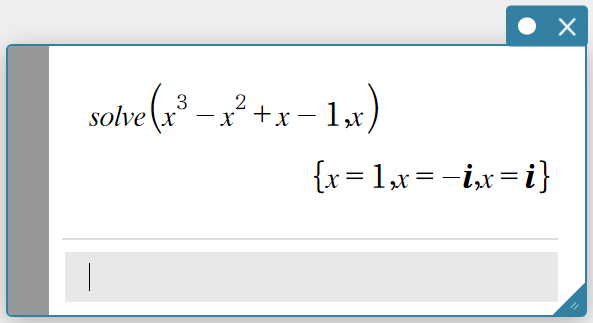
Using Answer Memory (ans)

Answer Memory automatically saves calculation results to a variable named “ans”.
“ans” stores the latest calculation result, which is overwritten whenever you perform a new calculation.

• To enter the “ans” variable into a calculation formula, click [ans] on the software keyboard.
• To recall the calculation result currently saved in “ans”, click [ans] on the software keyboard and then [Execute].

Example: To store the following calculation formula in answer memory: \(123+456\)

1. Create a Calculation sticky note and perform the calculation \(123+456\).
2. Enter \(789-[{\rm ans}]\). On the software keyboard, click [Execute].
   
   This displays \(210\) as the calculation result.
3. Enter \([{\rm ans}] \div 7\). On the software keyboard, click [Execute].
   
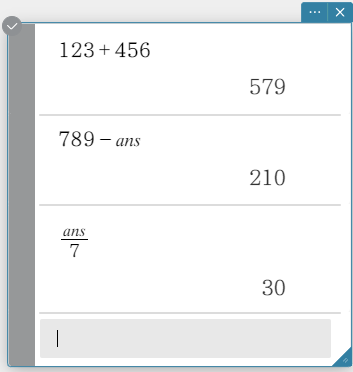
   This displays \(30\) as the calculation result.
   

MEMO
If answer memory does not contain a calculation result, it contains \(0\).
Separate ans memory contents are saved for each sticky note. You cannot share ans memory contents among different sticky notes.

You cannot use Variable Manager to view the contents of answer memory.
Entering an addition (\(+\)), subtraction (\(-\)), multiplication (\(\times\)), or division (\(\div\)) symbol while a calculation result is displayed will automatically enter “ans”.

Using Variables

• Variable Name Rules
  The following are the rules that apply to variable names.
  
  • Variable names can be up to 8 bytes long.
  • The following characters are allowed in a variable name: Uppercase and lowercase characters, subscript characters, numbers.
  • Variable names are case-sensitive. For example, each of the following is treated as a different variable name: abc, Abc, aBc, ABC.
• To store a value in a variable
  The syntax for the operation to store a value in a variable is shown below.
  [⇒] [Execute]

Example 1: Store the value \(10\) in variable “abc”, and then recall the stored value.

1. Create a Math sticky note.
2. Enter the following: \(10\)⇒abc.
   Use the [Math] keyboard to enter “⇒”.
   
3. On the software keyboard, click [Execute].
   
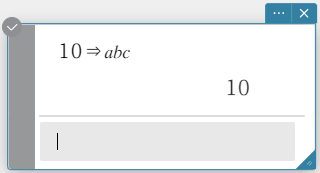
   This assigns the value “\(10\)” to the variable “abc”.
4. Enter the following: abc.
5. On the software keyboard, click [Execute].
   
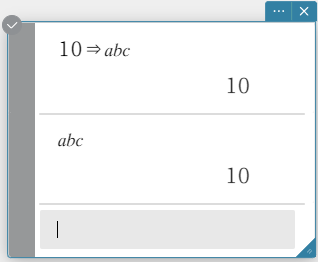
   This recalls the value (“\(10\)”) stored in variable “abc”.
   

MEMO
When storing a value in a variable, you could also use the [\(:=\)] key in place of [⇒]. This would result in the input syntax shown below.
[\(:=\)] [Execute]
Example: To store the value \(123\) in variable “\(x\)” by using “\(:=\)”
① Create a Math sticky note.
② Enter the following: \(x:=123\).
－ Use the [Number] keyboard to enter “\(:=\)”.

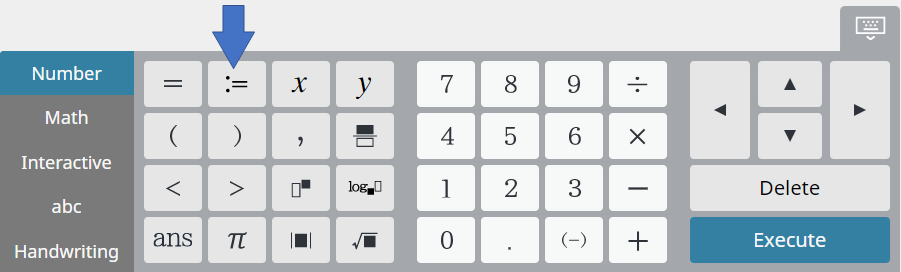
③ On the software keyboard, click [Execute].

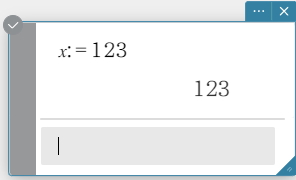
－ This assigns the value “\(123\)” to the variable “\(x\)”.
To check the variable in which the value is stored, click > [Variable Manager] in the Paper header. For details, see “Using Variable Manager”.

Using Variable Manager

• To start up Variable Manager

1. Click in the Paper header.
   
2. Click [Variable Manager].
   
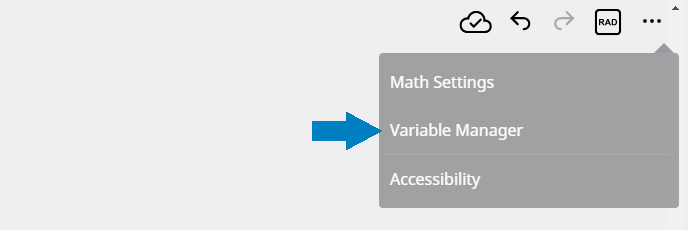
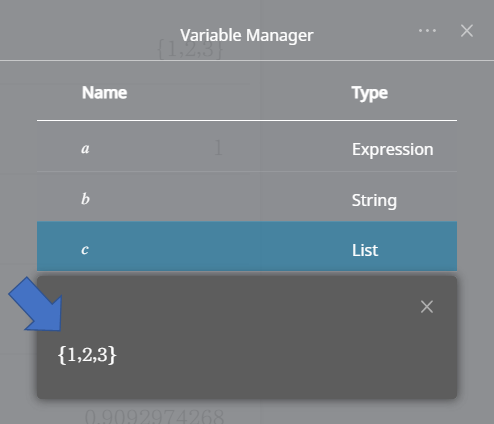
   This displays the Variable Manager dialog box, which shows a list of variables.
   
   ①Variable names
   ②Variable types (See below.)
   Expression … Real number, complex number or expression data
   String … String data
   List … List data
   Matrix … Matrix data
   Function … User-defined function
   Clicking a variable name displays its value.
   

Using the Interactive Menu

The Interactive Menu displays a dialog box in accordance with the function you are using. You can use the dialog box to enter the arguments required by a function, and to configure function calculation settings. The input fields and settings that appear in the dialog box vary depending on the function.

• Interactive Menu Configuration

The table below shows functions that can be entered with the Interactive Menu and their categories.

Category 1	Category 2	Functions
Transformation >		simplify
		expand
	Factor >	factor
		rFactor
		factorOut
		combine
	Fraction >	propFrac
Advanced >		solve
		dSolve
		taylor
		laplace
		fourier
		invFourier
Calculation >		diff
		∫
		lim
		Σ
		Π
	line >	tanLine
		normal
		arcLen
	fMin/fMax >	fMin
		fMax
List >	Create >	seq
		listToMat
	Statistics >	min
		max
		mean
		median
		mode
		Q1
		Q3
		percentile
	Calculation >	sum
		prod
		sequence
		sumSeq
Matrix >	Create >	subMat
		listToMat
	Row & Column >	mRowAdd
Vector >		unitV
		angle
		norm
		crossP
		dotP
		toRect
		toPol
		toSph
		toCyl
Equation/Inequality >		solve
		dSolve
		rewrite
		exchange
		absExpand
Distribution/inv.Dist >	Continuous >	normPDf
		normCDf
	Discrete >	binomialPDf
		binomialCDf
	Inverse >	invNormCDf
		invBinomialCDf

Inserting Subscript

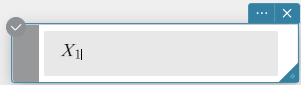
1. Move a cursor to a location where you want to insert a subscript.
   
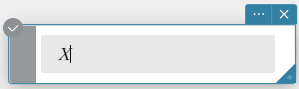
2. On your computer keyboard, press underscore key ([ _ ]).
   
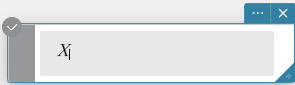
3. Enter \(1\).
   This is entered as the text shown below.
   
   MEMO
   In step 2 of the above procedure, you could also press the underscore key ([ _ ]) of the [abc] keyboard.
   Characters that can be subscripted are uppercase and lowercase alphanumeric characters.

Configuring Calculation Settings

1. Click in the Paper header.
   
2. Click [Math Settings].
   
   This displays the Math Settings dialog box.
   
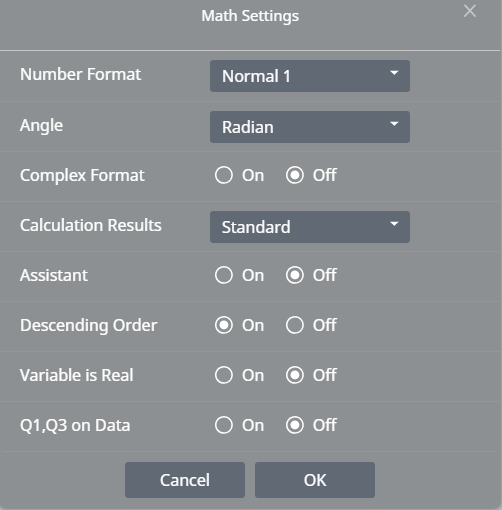
   You can use this screen to configure the settings below.
   
   
   Number Format
   Specifies the number of digits for display of a calculation result.
   Normal 1: Automatically uses exponential notation when calculation result \(x\) is in the
   range of \(10^{-2} >|x|, |x| \geq 10^{10}\)
   Normal 2: Automatically uses exponential notation when calculation result \(x\) is in the
   range of \(10^{-9} >|x|, |x| \geq 10^{10}\)
   Fix 0 – Fix 9: Specifies the number of decimal places for calculation results.
   Sci 0 – Sci 9: Specifies the number of significant digits and the exponent for calculation results. Specifying Sci 0 makes the number of significant digits 10.
   
   Angle
   Specifies the angle unit as radians, degrees, or grads.
   
   MEMO
   You can use the icons in the Paper header to check the current angle setting (: degrees, : radians, : grads). You can change the setting by clicking an icon.
   
   Complex number calculations
   On: Performs complex number calculations.
   Off: Performs real number calculations.
   
   Calculation Results
   Decimal: Displays calculation results using decimal fractions.
   Standard: Displays calculation results using numerical fractions (in a format including fractions, √, and/or π).
   MEMO
   You can use the icons in the Paper header to check the current calculation result display settings (: Standard, : Decimal).
   You can change the setting by clicking an icon.
   
   
   Selecting [Advanced] displays the advanced settings.
   
   
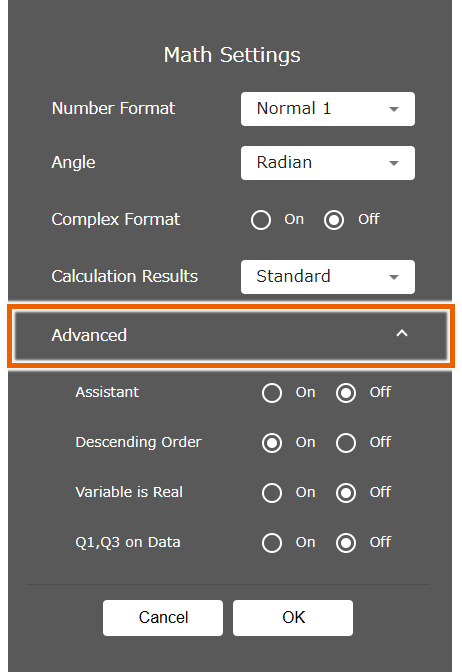
   Assistant
   On: Enters the Assistant Mode.
   Off: Enters the Algebra Mode.
   Algebra Mode, calculation result expressions are automatically simplified. Expressions are not simplified in the Assistant Mode.
   
   Expression 1： \(x^2+2x+3x+6\)
   Assistant Mode
   \(x^2\) \(+2·x+3·x+6\)
   Algebra Mode
   \(x^2+5·x+6\)
   Expression 2： \({\rm expand} \left(\left(x+1\right)^2\right)\)
   Assistant Mode
   \(x^2+2·x·1+1^2\)
   Algebra Mode
   \(x^2+2·x+1\)
   Expression 3： \(x+1\) （When \(1\) is assigned to \(x\)）
   Assistant Mode
   \(x+1\)
   Algebra Mode
   \(2\)
   
   Descending Order
   On: Calculation result expressions are displayed in descending order.
   (Example: \(x^2 + x + 1\))
   Off: Calculation result expressions are displayed in ascending order.
   (Example: \(1 + x + x^2\))
   
   Variable is Real
   On: Variables are treated as real numbers.
   Off: Variables are treated as complex numbers.
   
   Q1, Q3 on Data
   On: Statistical Q1 and Q3 are calculated using French calculation rules.
   Off: Statistical Q1 and Q3 are calculated using standard calculation rules.
   
3. After the settings are the way you want, click [OK].
   
   MEMO
   Initial default settings are shown below.
   Number Format: Normal 1
   Angle: Radian
   Complex Format: Off
   Calculation Results: Standard
   Assistant: Off
   Descending: On
   Variable is Real: Off
   Q1, Q3 on Data: Off